线性最小二乘法迭代拟合(梯度下降)目标
找到最佳的斜率 aaa 和截距 bbb,使得直线
y=ax+b y = ax + b y=ax+b
尽可能接近所有数据点 (xi,yi)(x_i, y_i)(xi,yi)。
1. 定义损失函数(误差)
使用均方误差 衡量拟合好坏:
L(a,b)=12n∑i=1n(axi+b−yi)2 L(a, b) = \frac{1}{2n} \sum_{i=1}^{n} (a x_i + b - y_i)^2 L(a,b)=2n1i=1∑n(axi+b−yi)2
- 值越小,拟合越好;
- 因子 12\frac{1}{2}21 仅为求导时简化表达式。
2. 计算梯度
梯度表示误差对参数的变化率:
-
对斜率 aaa 的偏导:
∂L∂a=1n∑i=1n(axi+b−yi)⋅xi \frac{\partial L}{\partial a} = \frac{1}{n} \sum_{i=1}^{n} (a x_i + b - y_i) \cdot x_i ∂a∂L=n1i=1∑n(axi+b−yi)⋅xi -
对截距 bbb 的偏导:
∂L∂b=1n∑i=1n(axi+b−yi) \frac{\partial L}{\partial b} = \frac{1}{n} \sum_{i=1}^{n} (a x_i + b - y_i) ∂b∂L=n1i=1∑n(axi+b−yi)
梯度指向误差增长最快的方向 ,因此需反方向更新参数。
3. 迭代更新参数(梯度下降)
每次按以下规则调整参数:
a←a−η⋅∂L∂ab←b−η⋅∂L∂b \begin{aligned} a &\leftarrow a - \eta \cdot \frac{\partial L}{\partial a} \\ b &\leftarrow b - \eta \cdot \frac{\partial L}{\partial b} \end{aligned} ab←a−η⋅∂a∂L←b−η⋅∂b∂L
其中:
- η>0\eta > 0η>0 是学习率(如 0.001);
- 控制每一步更新的步长。
4. 重复直到收敛
不断循环:
- 计算当前预测值 y^i=axi+b\hat{y}_i = a x_i + by^i=axi+b;
- 计算梯度;
- 更新 aaa 和 bbb;
随着迭代进行,损失 L(a,b)L(a,b)L(a,b) 逐渐减小,直线逐步逼近最优拟合。
💡 关键点总结
- 梯度下降是迭代优化方法,不是直接求解解析解;
- 除以 nnn 是为了使用平均误差,使结果与样本数量无关;
- 即使数据完全在一条直线上,也需要多次迭代才能接近真实参数;
- 学习率 η\etaη 需合理选择:
- 太大 → 震荡甚至发散;
- 太小 → 收敛速度慢。
💡Matlab代码
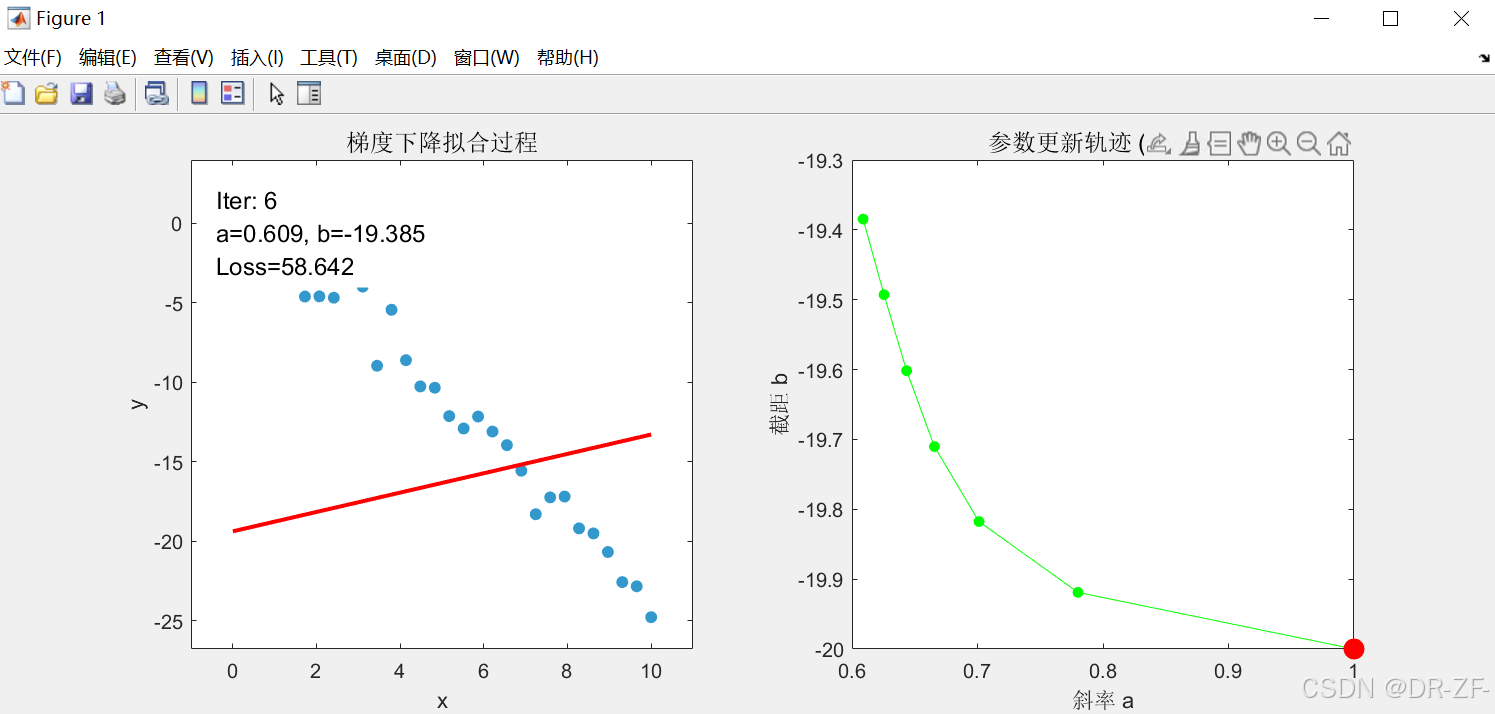
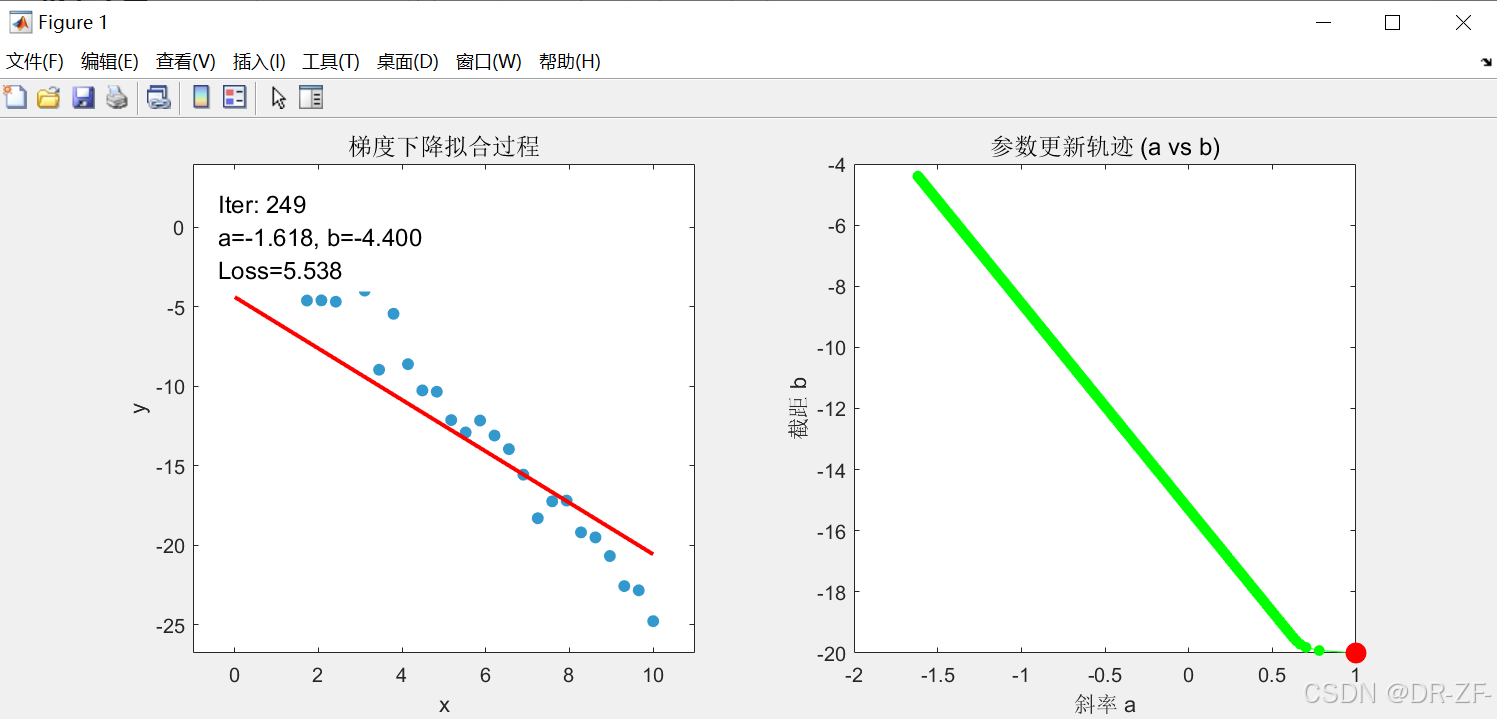
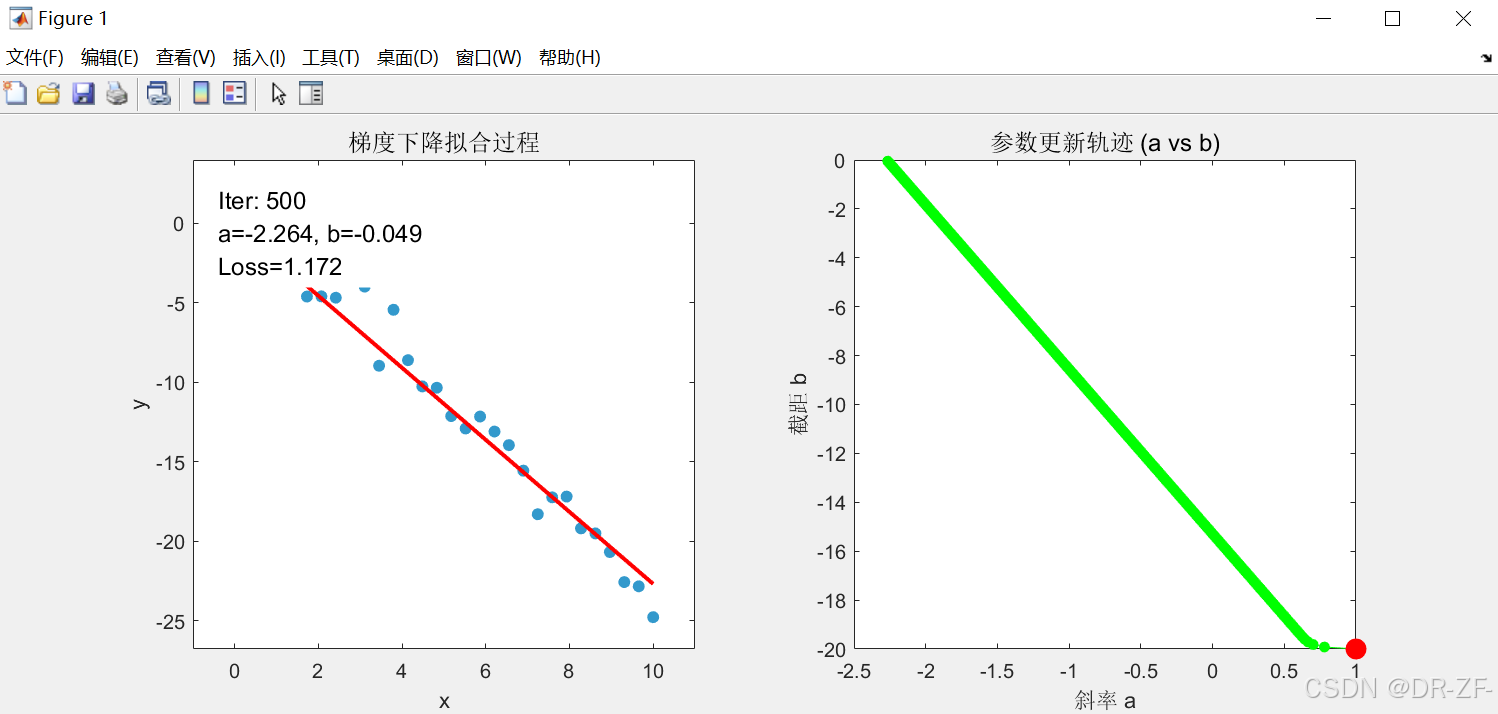
matlab
%% 梯度下降动画:最小二乘直线拟合(修复起点显示问题)
clear; close all; clc;
% 生成带噪声的线性数据
rng(0); % 可复现
n = 30;
x = linspace(0, 10, n)';
y_true = -2.5 * x + 1.0; % 真实直线
y = y_true + randn(n,1) * 1; % 添加高斯噪声
% 初始化参数
a = 1; % 初始斜率
b = -20; % 初始截距
lr = 0.02; % 学习率(可调)
max_iter = 500;
% 存储历史用于绘制轨迹
a_hist = zeros(max_iter+1, 1);
b_hist = zeros(max_iter+1, 1);
loss_hist = zeros(max_iter+1, 1);
a_hist(1) = a;
b_hist(1) = b;
loss_hist(1) = sum((a*x + b - y).^2) / (2*n);
% 创建图形窗口
figure('Position', [100, 100, 1000, 400]);
% === 左图:数据与拟合直线 ===
subplot(1,2,1); hold on; box on;
scatter(x, y, 'filled', 'MarkerFaceColor', [0.2 0.6 0.8]);
title('梯度下降拟合过程', 'FontSize', 12);
xlabel('x'); ylabel('y');
xlim([min(x)-1, max(x)+1]); ylim([min(y)-2, max(y)+2]);
h_line = plot(x, a*x + b, 'r-', 'LineWidth', 2);
h_text = text(0.05, 0.95, '', 'Units','normalized', 'FontSize',12,...
'VerticalAlignment','top','BackgroundColor','white');
% === 右图:参数空间轨迹(先初始化坐标轴)===
subplot(1,2,2); hold on; box on;
title('参数更新轨迹 (a vs b)', 'FontSize', 12);
xlabel('斜率 a'); ylabel('截距 b');
% === 显示初始状态(关键!)===
set(h_line, 'YData', a*x + b);
set(h_text, 'String', sprintf('Iter: %d\na=%.3f, b=%.3f\nLoss=%.3f', ...
0, a, b, loss_hist(1)));
% 在右图绘制初始点(用红色大圆点高亮起点)
subplot(1,2,2);
plot(a_hist(1), b_hist(1), 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');
drawnow;
pause(1.0); % 停顿1秒,让用户看清初始猜测
% === 开始迭代优化 ===
for k = 1:max_iter
% 前向预测
y_pred = a * x + b;
% 计算梯度
da = sum((y_pred - y) .* x) / n; % ∂L/∂a
db = sum(y_pred - y) / n; % ∂L/∂b
% 更新参数
a = a - lr * da;
b = b - lr * db;
% 记录历史
a_hist(k+1) = a;
b_hist(k+1) = b;
loss_hist(k+1) = sum((a*x + b - y).^2) / (2*n);
% 更新左图:拟合直线和文字
set(h_line, 'YData', a*x + b);
set(h_text, 'String', sprintf('Iter: %d\na=%.3f, b=%.3f\nLoss=%.3f', ...
k, a, b, loss_hist(k+1)));
% 更新右图:清空后重绘整条轨迹
subplot(1,2,2);
cla; % 清除当前坐标轴,防止线条叠加变粗
hold on; box on;
title('参数更新轨迹 (a vs b)', 'FontSize', 12);
xlabel('斜率 a'); ylabel('截距 b');
% 绘制完整轨迹(绿色线+点)
plot(a_hist(1:k+1), b_hist(1:k+1), 'go-', ...
'MarkerFaceColor', 'g', 'MarkerSize', 5);
% 重新高亮起点(可选,保持红色)
plot(a_hist(1), b_hist(1), 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');
drawnow;
pause(0.05); % 控制动画速度
end
fprintf('最终结果: a = %.4f, b = %.4f (真实值: a=-2.5, b=1.0)\n', a, b);