STM32F103通过L298N驱动两相4线步进电机【42步进电机】

一、效果演示

L298N驱动42步进电机

二、准备阶段

（stm32单片机，L298N模块，42步进电机，螺丝刀，杜邦线，串口工具）
1）主控：stm32f103c8t6
2）驱动器 : L298N

3）电机:42步进电机

4）驱动方式：4拍驱动

三、原理介绍和接线描述

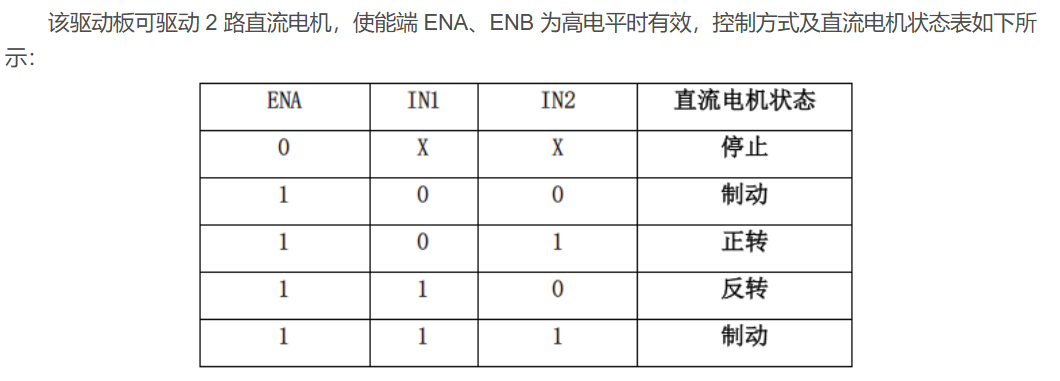
1）L298N的输入和输出

2）步进电机线序【我用的电机是淘宝买的，商家提供的手册描述了线序】

3）步进电机4拍驱动

概念扫盲：
拍数 ------转子转动一周，定子绕组通电的次数，以两相电机为例，有两相四拍运行方式即**(A+)---(B+)---(A-)---(B-）**，
步距角 ------步进电机接收到一个脉冲信号后，驱动电机按设定的方向转动的一个固定角度。如两相四线步进电机的基本步距角是1.8°，即一个脉冲走1.8°。
细分 -----同时，为了减弱或消除步进电机的低频振动开发了细分驱动技术。细分后电机运行时的实际步距角是基本步距角的几分之一，微步即1/4-step、1/8-step、1/16-step等。比如，两相步进电机的基本步距角是1.8°，如果没有细分，则是200个脉冲走一圈360°。细分是通过驱动器靠精确控制电机的相电流所产生的，如果是10细分，则发一个脉冲电机走0.18°，即2000个脉冲走一圈360°，电机的精度能否达到或接近0.18°，还取决于细分驱动器的细分电流控制精度等其它因素。

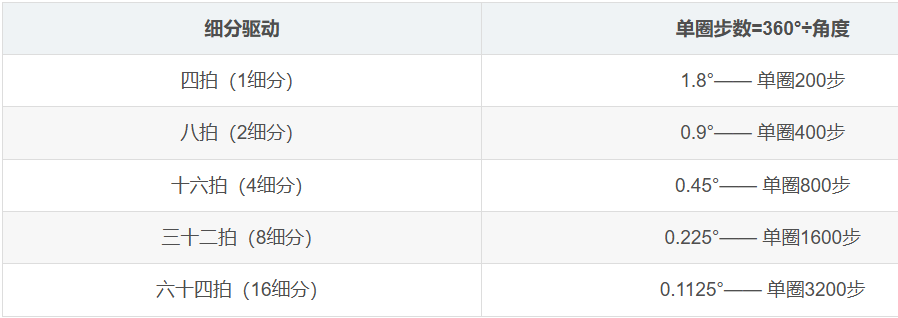
结论1：用四拍驱动，执行一个周期(A+)---(B+)---(A-)---(B-），则电机运行1.8°，运行200个周期，电机旋转360度，即1圈

4）根据 "L298N特性" 和 "步进电机线序" 和"步进电机4拍驱动特性"，分析怎样配置mcu的输出 ****

这是对接线图的简化：

步进电机4根线：A+,A-，B+，B-

L298N4个输出：out1,out2,out3,out4

按照这个图片中的顺序连接；

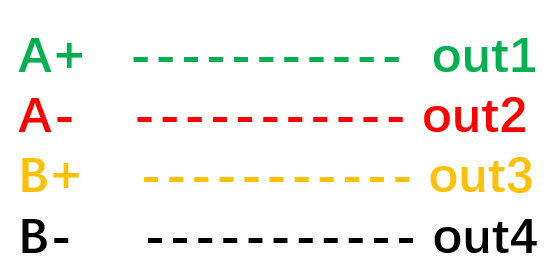
为什么按这个顺序连接？-----因为提供4拍的时序分析出来的

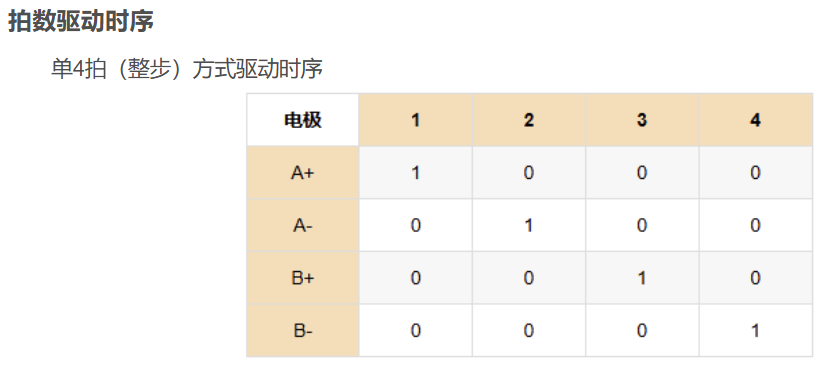
这个图是4拍的时序，

A+连上一个L298N的输出（out1），

A-连上一个L298N的输出（out2），

B+连上一个L298N的输出（out3），

B-连上一个L298N的输出（out4），

//这样写方便写程序（如果用其他接线方法，就要根据时序写相应的程序）。

四、代码

我使用的这4个引脚：

PA10（IN1），

PA11（IN2），

PA12（IN3），

PA15（IN4），

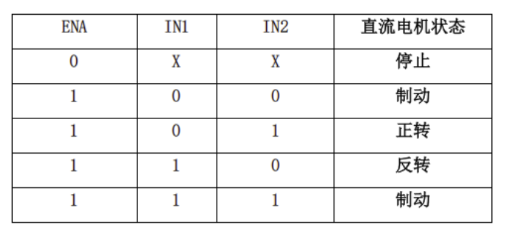
L298N的情况是：

IN1 高 && IN2低 --->out1输出高

IN1 低 && IN2高 --->out2输出高

IN3 高 && IN4低 --->out3输出高

IN3 低 && IN4高 --->out4输出高

由于连接线序为

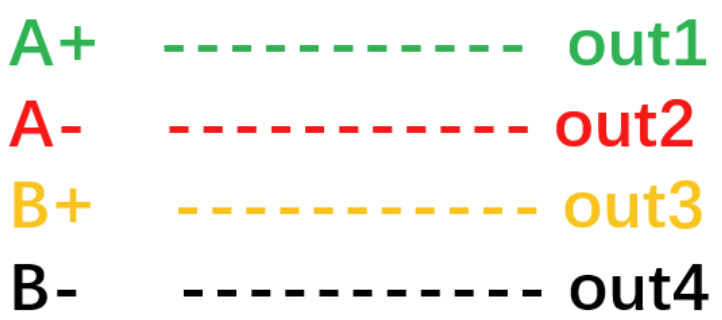
所以我们根据4拍的时序(A+)---(B+)---(A-)---(B-）得出：L298N的输入信号（即mcu的输出信号，一个周期的规律入如下）

通过宏定义了A1，A2，B1，B2的接口

c 复制代码

#define  GPIO_PORTA_BASE GPIOA
#define A1(state) (state>0) ? HAL_GPIO_WritePin(GPIO_PORTA_BASE, GPIO_PIN_10, GPIO_PIN_SET) :HAL_GPIO_WritePin(GPIO_PORTA_BASE, GPIO_PIN_10, GPIO_PIN_RESET)  //A+
#define B1(state) (state>0) ? HAL_GPIO_WritePin(GPIO_PORTA_BASE, GPIO_PIN_11, GPIO_PIN_SET) :HAL_GPIO_WritePin(GPIO_PORTA_BASE, GPIO_PIN_11, GPIO_PIN_RESET)  //B+
#define A2(state) (state>0) ? HAL_GPIO_WritePin(GPIO_PORTA_BASE, GPIO_PIN_12, GPIO_PIN_SET) :HAL_GPIO_WritePin(GPIO_PORTA_BASE, GPIO_PIN_12, GPIO_PIN_RESET)  //A-
#define B2(state) (state>0) ? HAL_GPIO_WritePin(GPIO_PORTA_BASE, GPIO_PIN_15, GPIO_PIN_SET) :HAL_GPIO_WritePin(GPIO_PORTA_BASE, GPIO_PIN_15, GPIO_PIN_RESET)  //B-

通过逻辑实现4拍和正反转

c 复制代码

int timeout_ms = 7;
void SetMotor_Four_Motor0(uint8_t Direction)
{
    static uint8_t i = 0;
    if(Direction>0)     //顺序
    {
        switch(i)
           {
               case 0:
               {
                   A1(1);B1(0);A2(0);B2(0);
                   HAL_Delay(timeout_ms);
                   break;
               }

               case 1:
               {
                   A1(0);B1(1);A2(0);B2(0);
                  HAL_Delay(timeout_ms);
                   break;
               }

               case 2:
               {
                   A1(0);B1(0);A2(1);B2(0); 
                   HAL_Delay(timeout_ms);


                   break;
               }

               case 3:
               {
                   A1(0);B1(0);A2(0);B2(1);
                   HAL_Delay(timeout_ms);
                   break;
               }
              }
    }
    else                //倒序
    {
        switch(i)
           {
               case 3:
               {
                   A1(1);B1(0);A2(0);B2(0);
                  HAL_Delay(timeout_ms);
                   break;
               }

               case 2:
               {
                   A1(0);B1(1);A2(0);B2(0); 
                   HAL_Delay(timeout_ms);

                   break;
               }

               case 1:
               {
                   A1(0);B1(0);A2(1);B2(0);
                   HAL_Delay(timeout_ms);

                   break;
               }

               case 0:
               {
                   A1(0);B1(0);A2(0);B2(1);
                   HAL_Delay(timeout_ms);

                   break;
               }
           }
           

    }
    i++;
    if(i>3)
        i=0;

}