线性回归与KNN算法的核心原理及实践应用

文章目录

线性回归与KNN算法的核心原理及实践应用
- 一、机器学习基础概念
- 二、线性回归分析
- - [2.1 相关关系与回归分析](#2.1 相关关系与回归分析)
  - [2.2 一元线性回归模型](#2.2 一元线性回归模型)
  - [2.3 误差项分析](#2.3 误差项分析)
  - [2.4 参数估计方法](#2.4 参数估计方法)
  - [2.5 模型评价指标](#2.5 模型评价指标)
- 三、K-近邻算法（KNN）
- - [3.1 算法原理](#3.1 算法原理)
  - [3.2 距离度量](#3.2 距离度量)
  - [3.3 算法优缺点](#3.3 算法优缺点)
- 四、实践案例
- - [4.1 一元线性回归实现](#4.1 一元线性回归实现)
  - [4.2 KNN算法实现](#4.2 KNN算法实现)
  - [4.3 鸢尾花分类案例](#4.3 鸢尾花分类案例)
- 五、模型评价与优化
- - [5.1 混淆矩阵](#5.1 混淆矩阵)

线性回归与KNN算法的核心原理及实践应用

一、机器学习基础概念

机器学习是人工智能的重要分支，通过对大量数据的学习和训练，让计算机具备预测和决策能力。数据量越大，最终训练结果越准确，针对不同的数据类型需要选择不同的数学模型。

二、线性回归分析

2.1 相关关系与回归分析

相关关系包含因果关系和平行关系：

因果关系：回归分析，原因引起结果，需要明确自变量和因变量
平行关系：相关分析，无因果关系，不区分自变量和因变量

2.2 一元线性回归模型

一元线性回归模型表示为：
y = β 0 + β 1 x + ε y = \beta_0 + \beta_1 x + \varepsilon y=β0+β1x+ε

其中：

β 0 \beta_0 β0 和 β 1 \beta_1 β1 是模型参数
ε \varepsilon ε 是误差项，代表除线性因素外的随机因素所产生的误差

2.3 误差项分析

误差项具有重要特性：

独立同分布：每个样本点独立且处于同一分布函数下
满足高斯分布：期望为0，方差为(\sigma^2)
不可省略：误差是必然产生的，且基于误差特点进行参数估计

2.4 参数估计方法

极大似然估计核心思想：极度自恋，相信自己看到的样本就是冥冥之中最接近真相的。通过似然函数最大化来估计参数。

最小二乘法 目标函数：
J ( β ) = 1 2 ∑ i = 1 m ( y ( i ) − β T X ( i ) ) 2 J(\beta) = \frac{1}{2} \sum_{i=1}^m (y^{(i)} - \beta^T X^{(i)})^2 J(β)=21∑i=1m(y(i)−βTX(i))2

2.5 模型评价指标

相关系数 （皮尔逊相关系数）：
r = ∑ ( x − x ‾ ) ( y − y ‾ ) ∑ ( x − x ‾ ) 2 ⋅ ∑ ( y − y ‾ ) 2 r = \frac{\sum(x - \overline{x})(y - \overline{y})}{\sqrt{\sum(x - \overline{x})^2 \cdot \sum(y - \overline{y})^2}} r=∑(x−x)2⋅∑(y−y)2 ∑(x−x)(y−y)

判定系数 (R^2) （拟合优度）：

取值范围在[0,1]之间，越接近1说明拟合效果越好

三、K-近邻算法（KNN）

3.1 算法原理

KNN算法是一种基于实例的学习方法，通过计算新样本与训练样本的距离，找到k个最近邻，根据这些邻居的类别进行投票决定新样本的类别。

3.2 距离度量

常用的距离公式包括：

欧氏距离（p=2）
曼哈顿距离（p=1）
闵可夫斯基距离（p可调节）

3.3 算法优缺点

优点：

简单，易于理解，易于实现，无需训练
适合对稀有事件进行分类
对异常值不敏感

缺点：

样本容量比较大时，计算时间很长
不均衡样本效果较差

四、实践案例

4.1 一元线性回归实现

python 复制代码

import pandas as pd
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression

data = pd.read_csv("data.csv")

# 绘制散点图
plt.scatter(data.广告投入, data.销售额)
plt.show()

# 建立回归模型
lr = LinearRegression()
x = data[['广告投入']]
y = data[['销售额']]
lr.fit(x, y)  # 训练模型

# 模型检验
result = lr.predict(x)
score = lr.score(x, y)

a = round(lr.intercept_[0], 2)  # 截距
b = round(lr.coef_[0][0], 2)    # 斜率
print("线性回归模型为：y = {}x + {}.".format(b, a))

# 利用回归模型进行预测
predict = lr.predict([[40], [45], [50]])
print(predict)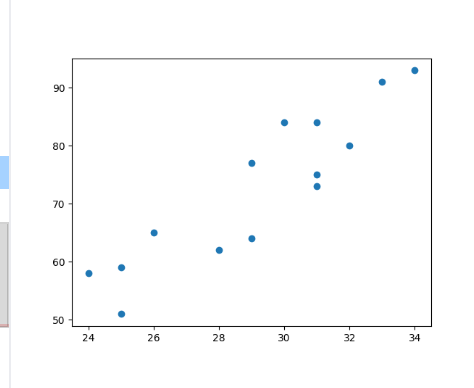

4.2 KNN算法实现

python 复制代码

import matplotlib.pyplot as plt
import numpy as np

# 读取数据
data = np.loadtxt('datingTestSet2.txt')
data_1 = data[data[:, -1] == 1]
data_2 = data[data[:, -1] == 2]
data_3 = data[data[:, -1] == 3]

# 数据可视化展示
fig = plt.figure()
ax = plt.axes(projection="3d")
ax.scatter(data_1[:, 0], data_1[:, 1], zs=data_1[:, 2], c="#00DDAA", marker="o")
ax.scatter(data_2[:, 0], data_2[:, 1], zs=data_2[:, 2], c="#FF5511", marker="^")
ax.scatter(data_3[:, 0], data_3[:, 1], zs=data_3[:, 2], c="#000011", marker="+")
ax.set(xlabel="Xaxes", ylabel="Yaxes", zlabel="Zaxes")
plt.show()

# KNN算法实现
from sklearn.neighbors import KNeighborsClassifier

data = np.loadtxt('datingTestSet2.txt')
X = data[:, :-1]  # 特征
y = data[:, -1]   # 标签
neigh = KNeighborsClassifier(n_neighbors=5)
neigh.fit(X, y)

print(neigh.predict([[19739, 2.816960, 1.686219]]))

# 多人同时预测
predict_data = [[9744, 11.440364, 0.760461],
                [16191, 0.100000, 0.605619],
                [42377, 6.519522, 1.058602],
                [27353, 11.475155, 1.528626]]

print("再次多人同时预测")
print(neigh.predict(predict_data))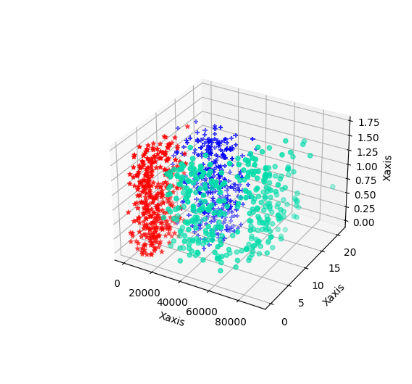

4.3 鸢尾花分类案例

python 复制代码

import pandas as pd

# 读取数据
train_data = pd.read_excel("鸢尾花训练数据.xlsx")
test_data = pd.read_excel("鸢尾花测试数据.xlsx")

# 处理训练集数据
train_X = train_data[['萼片长(cm)', '萼片宽(cm)', '花瓣长(cm)', '花瓣宽(cm)']]
train_y = train_data[['类型_num']]

# 数据标准化
from sklearn.preprocessing import scale

data = pd.DataFrame()
data['萼片长标准化'] = scale(train_X['萼片长(cm)'])
data['萼片宽标准化'] = scale(train_X['萼片宽(cm)'])
data['花瓣长标准化'] = scale(train_X['花瓣长(cm)'])
data['花瓣宽标准化'] = scale(train_X['花瓣宽(cm)'])

# KNN模型训练
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(train_X, train_y)

# 测试集预测
test_X = test_data[['萼片长(cm)', '萼片宽(cm)', '花瓣长(cm)', '花瓣宽(cm)']]
test_y = test_data[['类型_num']]

data_test = pd.DataFrame()
data_test['萼片长标准化'] = scale(test_X['萼片长(cm)'])
data_test['萼片宽标准化'] = scale(test_X['萼片宽(cm)'])
data_test['花瓣长标准化'] = scale(test_X['花瓣长(cm)'])
data_test['花瓣宽标准化'] = scale(test_X['花瓣宽(cm)'])

test_predicted = knn.predict(test_X)
score = knn.score(test_X, test_y)
print(score)

五、模型评价与优化

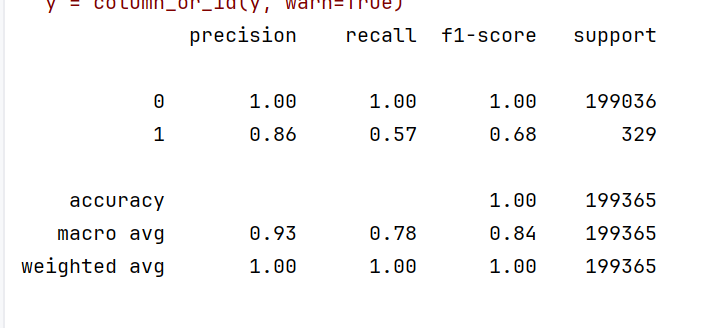
5.1 混淆矩阵

分类模型常用评价指标：

准确率（Accuracy）：(TP+TN)/(TP+TN+FP+FN)
精确率（Precision）：TP/(TP+FP)
召回率（Recall）：TP/(TP+FN)
F1-score：2·(precision·recall)/(precision+recall)
某模型训练结果示例