Pytorch--张量

张量

定义

张量从结构上来说就是一个多维的数据，其可以储存任意维度的元素，同时它和numpy的数组一样，都可以通过shape来显示维度大小，或者使用X(x1,x2...,xn)来表示某个元素的索引，但是，张量中的每一个元素都是一个更小的张量，而非像数组一样存在int或者float数据类型，同时张量还有自己的特性

特性	普通多维数组	深度学习中的张量
自动微分	通常不支持	核心特性！ 可自动计算梯度，这是神经网络训练（反向传播）的基石。
计算优化	通用计算	针对GPU（CUDA）等硬件进行深度优化，能极大加速大规模矩阵运算。
设备感知	通常只在CPU上	可以明确地在CPU 或GPU上创建和转移，以利用GPU的并行计算能力。
框架集成	独立的数据结构	与深度学习框架（如PyTorch、TensorFlow）的计算图、神经网络层等无缝集成。

此外张量和数组一样，可以使用ones，zeros来初始化张量类型的数据，也可以使用tensor来直接创建张量类型的数据

import torch

a = torch.ones(3)          # 创建一个大小为三的一维的张量类型
zeros = torch.zeros(2, 3)  # 2x3 全0矩阵
ones = torch.ones(2, 3)    # 2x3 全1矩阵
rand = torch.rand(2, 3)    # 2x3 随机矩阵 (0~1)
randn = torch.randn(2, 3)  # 2x3 标准正态分布

b = torch.tensor([4.0, 1.0], [5.0, 3.0], [2.0, 1.0])
# tensor([[4., 1.], [5., 3.], [2., 1.]])

同时张量在cpu和gpu上的储存值是不互通的，加入在cpu上创建一个张量，其不能直接在gpu上进行运算，需要使用to函数来转换

point_cpu = point_gpu.to(device = 'cpu')
point_gpu = point_cpu.to(device = 'cuda:0')    # 0表示电脑的第一个gpu

# or 

point_cpu = point_gpu.cpu
point_gpu = point_cpu.cuda(0)

其中to函数还可以用于张量转化数据类型

point_double = point_short.to(torch.double)
point_short = point_double.to(torch.short)

|----------------------------|-----------|
| torch.float32/torch.float | 32位浮点数 |
| torch.float64/torch.double | 64位双精度浮点数 |
| torch.float16/torch.half | 16位半精度浮点数 |
| torch.int8 | 8位有符号整数 |
| torch.uint8 | 8位无符号整数 |
| torch.int16/torch.short | 16位有符号整数 |
| torch.int32/torch.int | 32位有符号整数 |
| torch.int64/torch.long | 64位有符号整数 |
| torch.bool | 布尔型 |

一般创建的张量数据类型默认为32位浮点数(torch.float32/torch.float)

函数

output = torch.tensor(data, dtype, device, requires_grad, pin_memory)/output.tensor()

data:要输出的张量数据，可以是列表、元组、数组、标量和其他类型

dtype:可选，数据类型

device:可选，张量计算的设备

requires_grad:可选，bool型，是否需要自己微分，默认为False

pin_memory:可选，bool型，默认为False，是否设置固定的内存

张量元数据

大小、偏移量和步长

大小:表示为一个数组，表示张量形状即在每个维度上有多少个元素

可以使用tensor.shape()来得出

偏移量:指存储区中某个元素相对张量中的第一个元素的索引

可以使用tensor.storage_offset()来得出

步长:指存储区中为了获得下一个元素需要跳过的元素数量

可以使用tensor.stride()来得出
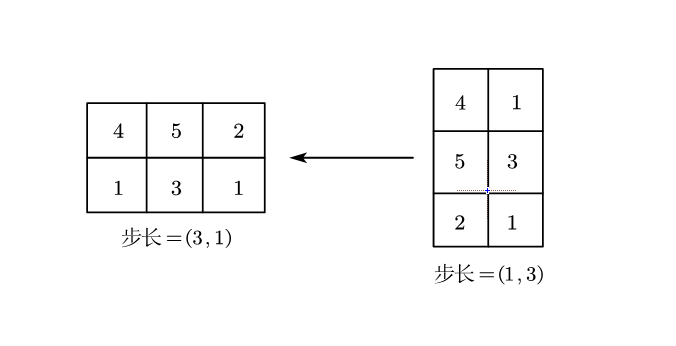
对于后面的转置运算，即便最后得到两个不同的张量，但是这两个张量共享同一个存储区，只是形状和步长上有所不同

points = ([[4.0, 1.0], [5.0, 3.0], [2.0, 1.0]])
points_t = points.T

print(points.storage()) == points_t.storage())        # True
print(points.shape()) == points_t.shape())            # False
# (2, 1)                 (1, 2)
print(points.stride()) == points_t.stride())          # False

上述代码的转变如下图

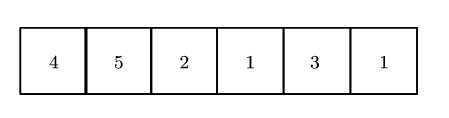
但是由于转置在存储区的位置不变，如下图

而步长即是从一个元素到达下一行/下一列最近的元素的距离

连续张量

对于某些函数来说需要只能对于连续张量使用，而连续张量即是在内存中按照行优先顺序连续储存的张量

通过定义我们可以知道，我们定义的张量一般都是连续张量，但是当对该张量进行转置后便不再连续，可以通过上面的图得到

可以改变张量的连续性的操作有：转置、切片和交换维度
可以通过tensor.is_contiguous()来判断是否为连续张量

也可以通过tensor.contiguous()来将不连续张量转化为连续张量，但是对于转置而言，转置不影响张量的存储区，但是通过tensor.contiguous()连续化后得到的新的张量与转置前的张量不在同一存储区

转化关系

张量类型和数组类型之间可以使用函数直接进行转化

import numpy as np
import torch

# NumPy 数组
np_array = np.array([[1, 2, 3], [4, 5, 6]])
print(type(np_array)) # <class 'numpy.ndarray'>
print(np_array.shape) # (2, 3)

# PyTorch 张量 (直接从NumPy数组转换而来)
torch_tensor = torch.from_numpy(np_array)
print(type(torch_tensor)) # <class 'torch.Tensor'>
print(torch_tensor.shape) # torch.Size([2, 3])

索引

常规索引

常规索引和python的list列表、numpy的nadarry数组一样

# points为张量
points[1:]    # 第1行之后的所有行，同时自动包含所有列
points[1:, :] # 同上
points[1:; 0] # 第1行之后的所有行，第1列
points[None]  # 增加一个维度，类似与unsqueeze()

广播特性

张量中最为独特的便是广播特性，对于后续的矩阵之间的数据处理或者运算，都存在广播特性

通俗点来讲，广播特性只有在矩阵的某一维度为1的情况下可以扩展广播

batch1 = torch.randn(5, 1, 3, 4)  # [5,1,3,4]
batch2 = torch.randn(1, 6, 4, 5)  # [1,6,4,5]

# 广播过程：
# 1. 对齐维度：都是4维，直接对齐
# 2. 比较维度：
#   维度0: 5 和 1 → 1可以广播到5
#   维度1: 1 和 6 → 1可以广播到6
#   维度2: 3 和 4 → 矩阵乘法：3×4 和 4×5
#   维度3: 4 和 5 → 矩阵乘法：3×4 和 4×5
# 3. 广播后：都变成 [5,6,3,4] 和 [5,6,4,5]
# 4. 矩阵乘法：[3,4] × [4,5] = [3,5]
# 5. 最终：批量维度 + 矩阵结果 = [5,6,3,5]

对于更复杂的广播也是如此

A = torch.randn(2, 1, 3, 1, 5, 4)  # [2,1,3,1,5,4]
B = torch.randn(1, 4, 1, 6, 4, 7)  # [1,4,1,6,4,7]

# 广播过程：
# 维度对齐（从右向左）：
#   A: [2,1,3,1,5,4]
#   B: [1,4,1,6,4,7]
# 
# 维度比较：
#   dim5: 4 和 7 → 矩阵乘法：5×4 和 4×7 = 5×7
#   dim4: 5 和 4 → 矩阵乘法：5×4 和 4×7
#   dim3: 1 和 6 → 1广播到6
#   dim2: 3 和 1 → 1广播到3
#   dim1: 1 和 4 → 1广播到4
#   dim0: 2 和 1 → 1广播到2
# 
# 广播后：都变成 [2,4,3,6,5,4] 和 [2,4,3,6,4,7]
# 矩阵乘法：[5,4] × [4,7] = [5,7]
# 最终形状：[2,4,3,6,5,7]

result = A @ B
print(f"结果形状: {result.shape}")  # [2,4,3,6,5,7]

对于上述的两个例子来说，真正的数据处理就在最后的两个维度之中，广播特性不会复制数据，只会扩展矩阵的维度使其满足运算的要求

而如果不满足维度等于1的条件，则会出现报错维度错误

# 最后两个维度不满足矩阵乘法规则
A = torch.randn(3, 4)  # [3,4]
B = torch.randn(3, 5)  # [3,5] 
# 报错，需要4×3，但这里是3×5

数据处理

规约运算

取平均数/相加

tensor.mean(dim, keepdim)/sum(dim, keepdim)

dim:可选，要处理的维度，不输入则默认为处理整体数据的平均值/求和

keepdim:可选，bool类型，默认为False，不保持原来的维度；True为保持原来的维度

import torch

img_t = torch.randn(3, 5, 5)        # 定义一个(3, 5 ,5)的张量，即是一个三通道的5×5的像素网格
print(img_t.mean(-3))               # 指定沿着某一个维度计算平均值，-3表示从后往前数第三个即第0个维度
# 输出一个5×5的张量

import torch

# 创建示例张量，更直观地观察计算过程
img_t = torch.tensor([
    # 通道0 (红色通道)
    [[1., 2., 3.],
     [4., 5., 6.],
     [7., 8., 9.]],
    
    # 通道1 (绿色通道)  
    [[10., 20., 30.],
     [40., 50., 60.],
     [70., 80., 90.]],
    
    # 通道2 (蓝色通道)
    [[100., 200., 300.],
     [400., 500., 600.],
     [700., 800., 900.]]
])

result = img_t.mean(-3)
print("结果形状:", result.shape)  # torch.Size([3, 3])
print("结果值:")
print(result)

# 输出：结果形状: torch.Size([3, 3])
        结果值:
                tensor([[ 37.,  74., 111.],
                        [148., 185., 222.],
                        [259., 296., 333.]])

其中输出结果的第一个元素是通过其他三个矩阵的第一个元素求平均得来的，即把3个通道的对应位置像素值取平均

sum和mean用法相同

所有元素乘积

torch.prod(tensor)--取所有元素乘积

torch.cumprod(tensor, dim)--按某一个维度取乘积

tensor:带计算的张量

dim:维度

tensor = torch.tensor([[1, 2, 3],
                       [4, 5, 6]])

print(torch.prod(tensor))          # 所有元素乘积: 720
print(torch.cumprod(tensor, dim=1)) # 累积积
# tensor([[ 1,  2,  6],
#         [ 4, 20, 120]])

标准差和方差

torch.std(tensor)--标志差

torch.var(tensor)--方差

tensor:带计算的张量

tensor = torch.tensor([[1, 2, 3],
                       [4, 5, 6]])

print(torch.std(tensor.float()))   # 标准差: 1.7078
print(torch.var(tensor.float()))   # 方差: 2.9167

数学运算--与matlab的矩阵运算类似

基本运算

加法/减法运算

a + b/torch.add(a, b) # 加法

a - b/torch.sub(a, b) # 减法
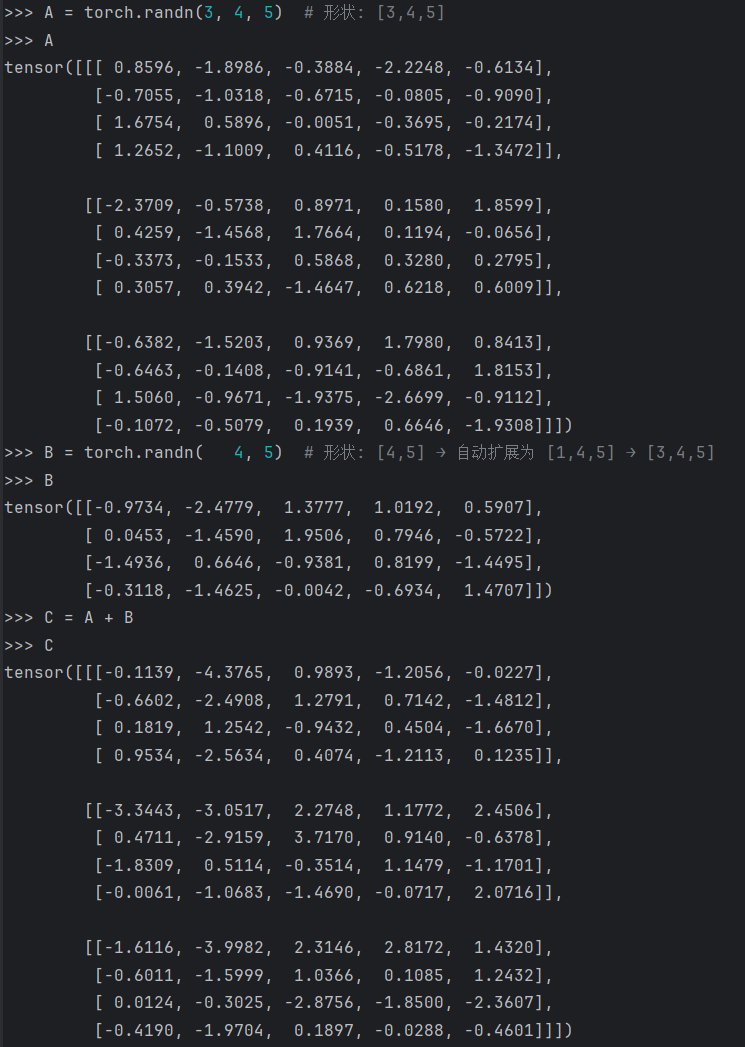
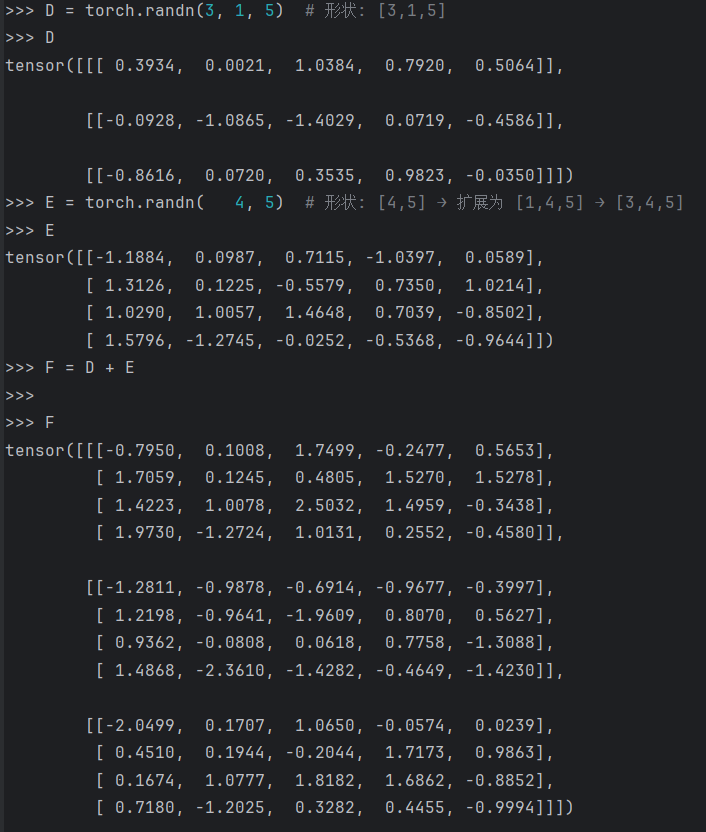
不一定需要相同维度，因为在不同的维度下，张量具有广播特性，可以扩展自己的维度

import torch

A = torch.randn(3, 4, 5)  # 形状: [3,4,5]
B = torch.randn(   4, 5)  # 形状: [4,5] → 自动扩展为 [1,4,5] → [3,4,5]
C = A + B 

D = torch.randn(3, 1, 5)  # 形状: [3,1,5]
E = torch.randn(   4, 5)  # 形状: [4,5] → 扩展为 [1,4,5] → [3,4,5]
F = D + E  # 可行!

可以看出张量的广播特征是按照自己输入的数据维度进行自我有规律的添加维度，运算后所得的张量为每个位置对应的最大维度

乘法/除法

a * b/torch.mul(a, b) # 乘法

b / a/torch.div(b, a) # 除法

逐个元素相乘

a = torch.tensor([1, 2, 3])
b = torch.tensor([4, 5, 6])
print(a * b)           # tensor([4, 10, 18])
print(b / a)           # tensor([4.0000, 2.5000, 2.0000])

指数运算

a ** c/pow(a, b)

a = torch.tensor([1, 2, 3])
c = 2
print(torch.pow(a, c)) # 平方: tensor([1, 4, 9])

若要计算自然指数e，则使用exp(a)即可

print(torch.exp(a))    # tensor([ 2.7183,  7.3891, 20.0855])

对数运算

a = torch.tensor([1, 2, 3])

print(torch.log(a.float()))    # 自然对数
print(torch.log10(a.float()))  # 以10为底

矩阵运算

矩阵运算也存在广播特性

矩阵乘法

A @ B/torch.matmul(A, B)

vector = torch.randn(4)
matrix = torch.randn(4, 5)

# 左边是一维：视为行向量 [1, 4]
result1 = vector @ matrix  # [1,4] × [4,5] = [1,5] → 移除维度 → [5]

对于1维的向量，其左边视为行向量，右边视为列向量，不会进行广播

a = torch.tensor([1, 2, 3])
b = torch.tensor([4, 5, 6])
a @ b
# tensor(32)

上述代码运算的过程是点积而非矩阵乘法

转置

tensor.T/tensor.transpose/tensor.permute

对于第一个函数来说，其只针对于二维的数据转置，而后面的函数则是针对于高维的数据

matrix = torch.randn(3, 4)
print(matrix.t().shape)      # 4x3（2D转置）
print(matrix.T.shape)        # 同上

# 高维转置
tensor_3d = torch.randn(2, 3, 4)
print(tensor_3d.transpose(1, 2).shape)  # 交换维度1和2: [2,4,3]
print(tensor_3d.permute(2, 0, 1).shape) # 重排维度: [4,2,3]

取最大值/最小值

torch.max(tensor, dim)/torch.min(tensor, dim)

tensor:带计算的张量

dim:可选，需要计算的维度，默认为所有值一起比较

tensor = torch.tensor([[1, 2, 3],
                       [4, 5, 6]])

# 最大值/最小值
print(torch.max(tensor))           # 最大值: 6
print(torch.min(tensor))           # 最小值: 1


# 带索引的最大值/最小值
values, indices = torch.max(tensor, dim=1)
print(f"每行最大值: {values}")      # tensor([3, 6])
print(f"最大值索引: {indices}")      # tensor([2, 2])

比较运算

a = torch.tensor([1, 2, 3, 4, 5])
b = torch.tensor([3, 3, 3, 3, 3])

# 比较运算
print(torch.eq(a, b))     # 相等: tensor([False, False,  True, False, False])
print(torch.ne(a, b))     # 不等: tensor([True, True, False, True, True])
print(torch.gt(a, b))     # 大于: tensor([False, False, False,  True,  True])
print(torch.lt(a, b))     # 小于: tensor([True, True, False, False, False])
print(torch.ge(a, b))     # 大于等于
print(torch.le(a, b))     # 小于等于

逻辑运算

# 逻辑运算
bool_tensor = torch.tensor([True, False, True])
print(torch.logical_and(bool_tensor, torch.tensor([True, True, False])))
# tensor([ True, False, False])

print(torch.logical_or(bool_tensor, torch.tensor([False, False, False])))
# tensor([ True, False,  True])

print(torch.logical_not(bool_tensor))
# tensor([False,  True, False])

增加维度/删除维度

tensor.unsqueeze(dim)/squeeze(dim)

dim:要插入新维度的位置索引，默认为第一维

import torch

x = torch.tensor([1, 2, 3])  # shape: [3]
print(f'原始张量 x: {x}, shape: {x.shape}')

# 在维度0（最外层）添加新维度 -> 变成一个1行3列的矩阵
x_0 = x.unsqueeze(0)  # 等价于 torch.unsqueeze(x, 0)
print(f'x.unsqueeze(0): {x_0}, shape: {x_0.shape}')  # shape: [1, 3]

# 在维度1（或维度-1）添加新维度 -> 变成一个3行1列的矩阵
x_1 = x.unsqueeze(1)  # 等价于 x.unsqueeze(-1)
print(f'x.unsqueeze(1): {x_1}, shape: {x_1.shape}')  # shape: [3, 1]

squeeze和unsqueeze用法相同

序列化张量

张量的储存文件.t文件一般不具备可操作性

保存张量

torch.save(tensor, path)

tensor:待保存的张量

path:保存的地址，一般保存为一个.t文件

torch.save(tensor, './data/outsensor.t')

# or

with open('./data/outsensor.t', 'wb') as f:
    torch.save(tensor, f)

加载张量

tensor = torch.load(path)

tensor:待加载的张量

path:加载的地址，一般加载为一个.t文件

tensor = torch.load('./data/outsensor.t')

# or

with open('./data/outsensor.t', 'wb') as f:
    tensor = torch.load(f)