线性回归是统计学和机器学习中最基础的回归分析方法,核心目标是构建自变量(特征)与连续型因变量(标签)之间的线性关系模型,通过拟合最优直线 / 超平面,实现对连续值的预测。以下是从核心定义到应用要点的全维度梳理:
一、核心定义与模型形式
1. 一元线性回归(单特征)
适用于单个特征预测单个连续标签,是线性回归的基础形式:
- 模型公式:y=wx+b+ϵ
- y:因变量(待预测的连续值,如糖尿病病情指数);
- x:自变量(单一特征,如血糖值);
- w:回归系数(斜率),表示x每变化 1 单位,y的平均变化量;
- b:截距,x=0时y的预测值;
- ϵ:随机误差(残差),表示模型无法解释的随机波动,服从均值为 0 的正态分布。
2. 多元线性回归(多特征)
适用于多个特征预测单个连续标签(如 10 个特征预测糖尿病病情),是实际场景中最常用的形式:
- 模型公式:y=w1x1+w2x2+...+wnxn+b+ϵ
- 矩阵简化形式:Y=XW+b+ϵ
- X:特征矩阵(nsamples×nfeatures),每行是一个样本,每列是一个特征;
- W:回归系数向量(nfeatures×1),每个元素对应一个特征的权重;
- Y:因变量向量(nsamples×1),包含所有样本的真实标签。
二、核心目标:最小化残差平方和
线性回归的优化目标是找到最优的W(系数)和b(截距),使得残差平方和(SSE)最小:
- 残差:单个样本的真实值与预测值的偏差,ei=yi−y^i(y^i为预测值);
- 残差平方和公式:min∑i=1n(yi−y^i)2=min∑i=1n(yi−(WXi+b))2;
- 核心逻辑:让预测值尽可能贴近真实值,偏差的平方和越小,模型拟合效果越好。
三、参数求解方法
1. 最小二乘法(解析解)
- 适用场景:低维数据(特征数少,如 < 100)、样本量适中,且特征无严重多重共线性;
- 求解公式(多元场景):W=(XTX)−1XTY(XT为X的转置,(XTX)−1为XTX的逆矩阵);
- 优缺点:计算直接、有明确数学解,但当XTX不可逆(如特征线性相关)时失效,且高维数据下矩阵求逆计算成本极高。
2. 梯度下降法(数值解)
- 适用场景:高维数据(特征数多,如 > 100)、大规模样本(如百万级);
- 核心逻辑:沿残差平方和的负梯度方向迭代更新参数,逐步逼近最优解;
- 常见变体:
- 批量梯度下降(BGD):每次用全量样本更新参数,稳定但速度慢;
- 随机梯度下降(SGD):每次用单个样本更新参数,速度快但波动大;
- 小批量梯度下降(MBGD):结合前两者,用部分样本(如 32/64 个)更新,兼顾速度与稳定性;
- 优缺点:无解析解限制,适配高维 / 大规模数据,但需调参(学习率、迭代次数等)。
四、模型评估指标
1. 拟合优度R2(决定系数)
- 核心含义:模型可解释的因变量变异占总变异的比例,取值范围(−∞,1];
- 公式:R2=1−∑i=1n(yi−yˉ)2∑i=1n(yi−y^i)2(yˉ为真实值的均值);
- 解读:
- R2=1:模型完美拟合,预测值完全等于真实值;
- 0<R2<1:模型能解释部分变异,值越接近 1,拟合效果越好;
- R2=0:模型预测效果等同于直接用均值预测,无解释能力;
- R2<0:模型效果差于均值预测,通常是模型选择错误(如用线性回归拟合非线性数据)。
2. 误差类指标
- 均方误差(MSE):MSE=n1∑i=1n(yi−y^i)2,反映预测值与真实值的平均平方偏差,值越小越好;
- 均方根误差(RMSE):RMSE=MSE,将误差还原为与因变量同量纲的单位,更易解读(如预测血糖时,RMSE=0.5 表示平均偏差 0.5mmol/L);
- 平均绝对误差(MAE):MAE=n1∑i=1n∣yi−y^i∣,对异常值的鲁棒性优于 MSE。
五、线性回归的基本假设(模型有效前提)
线性回归的可靠性依赖 4 个关键假设,违反假设会导致模型系数失真、预测失效:
1. 线性性
特征与因变量之间存在显著的线性关系(如血糖越高,糖尿病病情指数越高);
- 验证方法:绘制特征与因变量的散点图、计算相关系数(皮尔逊相关系数接近 ±1 则线性性强)。
2. 独立性
样本之间相互独立,无自相关性(如时间序列数据中 "今天的血糖值影响明天的血糖值" 则违反独立性);
- 验证方法:Durbin-Watson 检验(DW 值接近 2 则无自相关)。
3. 同方差性
残差的方差在所有样本上恒定,无 "异方差"(如低血糖样本的预测误差小,高血糖样本的预测误差大);
- 验证方法:绘制残差 - 预测值散点图,若残差无明显趋势则满足同方差性。
4. 正态性
残差服从正态分布(大部分残差集中在 0 附近,极端残差极少);
- 验证方法:绘制残差的 Q-Q 图、直方图,或进行 Shapiro-Wilk 正态性检验。
六、常见问题与解决方案
1. 多重共线性
- 问题:多个特征之间高度相关(如 "体重" 和 "BMI"),导致XTX不可逆,系数估计值不稳定、解释性失真;
- 解决方案:
- 特征选择:删除冗余特征(如删除 BMI,保留体重);
- 正则化:引入 L1(Lasso)/L2(Ridge)正则化,惩罚过大的系数;
- 主成分分析(PCA):将高维相关特征降维为低维不相关特征。
2. 过拟合
- 问题:模型在训练集上拟合极好(R2接近 1),但在测试集上效果极差,泛化能力弱;
- 诱因:特征数过多、样本量过少、无正则化约束;
- 解决方案:
- 简化模型:减少特征数量(如 Lasso 正则化自动筛选特征);
- 正则化:添加 L2(Ridge)正则化,限制系数大小;
- 增加样本量:扩充训练数据,降低模型对局部噪声的敏感度。
3. 欠拟合
- 问题:模型在训练集和测试集上的效果都差(R2接近 0);
- 诱因:特征与因变量无线性关系、特征数量不足、模型过于简单;
- 解决方案:
- 增加特征:引入更多与因变量相关的特征(如预测糖尿病时添加 "糖化血红蛋白" 特征);
- 非线性变换:对特征做多项式变换(如x→x2),拟合非线性趋势;
- 更换模型:若线性关系不成立,改用非线性模型(如决策树、神经网络)。
七、适用场景与局限性
1. 适用场景
- 因变量为连续值(如血糖、房价、销售额);
- 特征与因变量存在线性 / 近似线性关系;
- 对模型解释性要求高(线性回归的系数可直接解释 "特征对因变量的影响方向和程度");
- 数据量适中、特征维度不高(或已做降维处理)。
2. 局限性
- 无法拟合非线性关系(如 "温度 - 销量" 的抛物线关系);
- 对异常值敏感(极端值会大幅影响系数估计);
- 对多重共线性敏感,需提前处理特征相关性;
- 仅适用于回归任务,无法解决分类问题(需结合 Sigmoid 函数扩展为逻辑回归)。
八、核心总结
线性回归的核心是 "线性假设 + 最小二乘优化",是回归任务的 "入门基准模型":
- 优势:原理简单、解释性强、计算成本低,是理解回归分析的基础;
- 关键:使用前需验证线性假设、处理异常值 / 多重共线性,使用中需通过正则化避免过拟合,使用后需用R2、RMSE 等指标评估效果;
- 延伸:线性回归是逻辑回归、岭回归、Lasso 回归等算法的基础,掌握线性回归是理解更复杂回归模型的核心前提。
实例:糖尿病患者的预测
python
import numpy as np
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import r2_score, mean_squared_error
from sklearn.model_selection import train_test_split
class MyLinearRegression:
def __init__(self):
self.coef_ = None # 回归系数(对应10个特征的w1-w10)
self.intercept_ = None # 截距(对应b)
def fit(self, X, y):
"""
训练模型:用最小二乘法求解参数
X: 特征矩阵 (n_samples, n_features)
y: 标签向量 (n_samples,)
"""
# 步骤1:给X添加截距列(全1列),对应b的系数
X_with_intercept = np.hstack([np.ones((X.shape[0], 1)), X])
# 步骤2:最小二乘法公式求解参数 W = (X^T X)^-1 X^T y
# X^T X:特征的协方差矩阵,(X^T X)^-1:逆矩阵,X^T y:特征与标签的协方差
X_T = X_with_intercept.T
try:
X_T_X_inv = np.linalg.inv(X_T @ X_with_intercept) # 矩阵求逆
except np.linalg.LinAlgError:
# 若矩阵不可逆(特征线性相关),用伪逆
X_T_X_inv = np.linalg.pinv(X_T @ X_with_intercept)
W = X_T_X_inv @ X_T @ y
# 拆分截距和系数:W[0]是截距,W[1:]是10个特征的系数
self.intercept_ = W[0]
self.coef_ = W[1:]
def predict(self, X):
"""预测:y = w1x1 + w2x2 + ... + w10x10 + b"""
return X @ self.coef_ + self.intercept_
# ---------------------- 1. 读取CSV数据 ----------------------
df = pd.read_csv("糖尿病数据.csv")
# 检查缺失值(必须处理,否则矩阵运算报错)
if df.isnull().any().any():
df = df.fillna(df.mean()) # 缺失值用均值填充(简单有效)
# 拆分特征(X)和标签(y):前10列是特征,最后1列是结果
X = df.iloc[:, :-1].values # (n_samples, 10)
y = df.iloc[:, -1].values # (n_samples,)
# ---------------------- 2. 数据预处理(标准化) ----------------------
# 线性回归对尺度敏感,10个特征需标准化(Z-score)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X) # 标准化后的特征
# 划分训练集/测试集(避免过拟合,验证模型泛化能力)
X_train, X_test, y_train, y_test = train_test_split(
X_scaled, y, test_size=0.2, random_state=42 # 20%作为测试集
)
# ---------------------- 3. 训练手动实现的线性回归 ----------------------
my_lr = MyLinearRegression()
my_lr.fit(X_train, y_train)
# 输出参数:10个特征的系数 + 截距
print("=== 手动实现线性回归参数 ===")
print(f"截距 b = {my_lr.intercept_:.4f}")
for i in range(10):
print(f"特征{i + 1}的系数 w{i + 1} = {my_lr.coef_[i]:.4f}")
# ---------------------- 4. 预测与评估 ----------------------
# 训练集预测
y_train_pred = my_lr.predict(X_train)
# 测试集预测
y_test_pred = my_lr.predict(X_test)
# 评估指标(拟合优度R²、均方误差MSE)
print("\n=== 模型评估结果 ===")
# 训练集
print(f"训练集 R² = {r2_score(y_train, y_train_pred):.4f}")
print(f"训练集 MSE = {mean_squared_error(y_train, y_train_pred):.4f}")
# 测试集(关键:泛化能力)
print(f"测试集 R² = {r2_score(y_test, y_test_pred):.4f}")
print(f"测试集 MSE = {mean_squared_error(y_test, y_test_pred):.4f}")
# ---------------------- 5. 对比sklearn官方实现(验证正确性) ----------------------
from sklearn.linear_model import LinearRegression
sk_lr = LinearRegression()
sk_lr.fit(X_train, y_train)
print("\n=== sklearn官方线性回归参数(对比验证) ===")
print(f"截距 b = {sk_lr.intercept_:.4f}")
for i in range(10):
print(f"特征{i + 1}的系数 w{i + 1} = {sk_lr.coef_[i]:.4f}")
# 对比预测结果(应几乎一致)
sk_y_test_pred = sk_lr.predict(X_test)
print(f"\nsklearn测试集 R² = {r2_score(y_test, sk_y_test_pred):.4f}")
# 加L2正则(Ridge)优化(手动实现可参考,或直接用sklearn)
from sklearn.linear_model import Ridge
ridge_lr = Ridge(alpha=1.0) # alpha越大,正则化越强
ridge_lr.fit(X_train, y_train)
print(f"Ridge测试集 R² = {r2_score(y_test, ridge_lr.predict(X_test)):.4f}")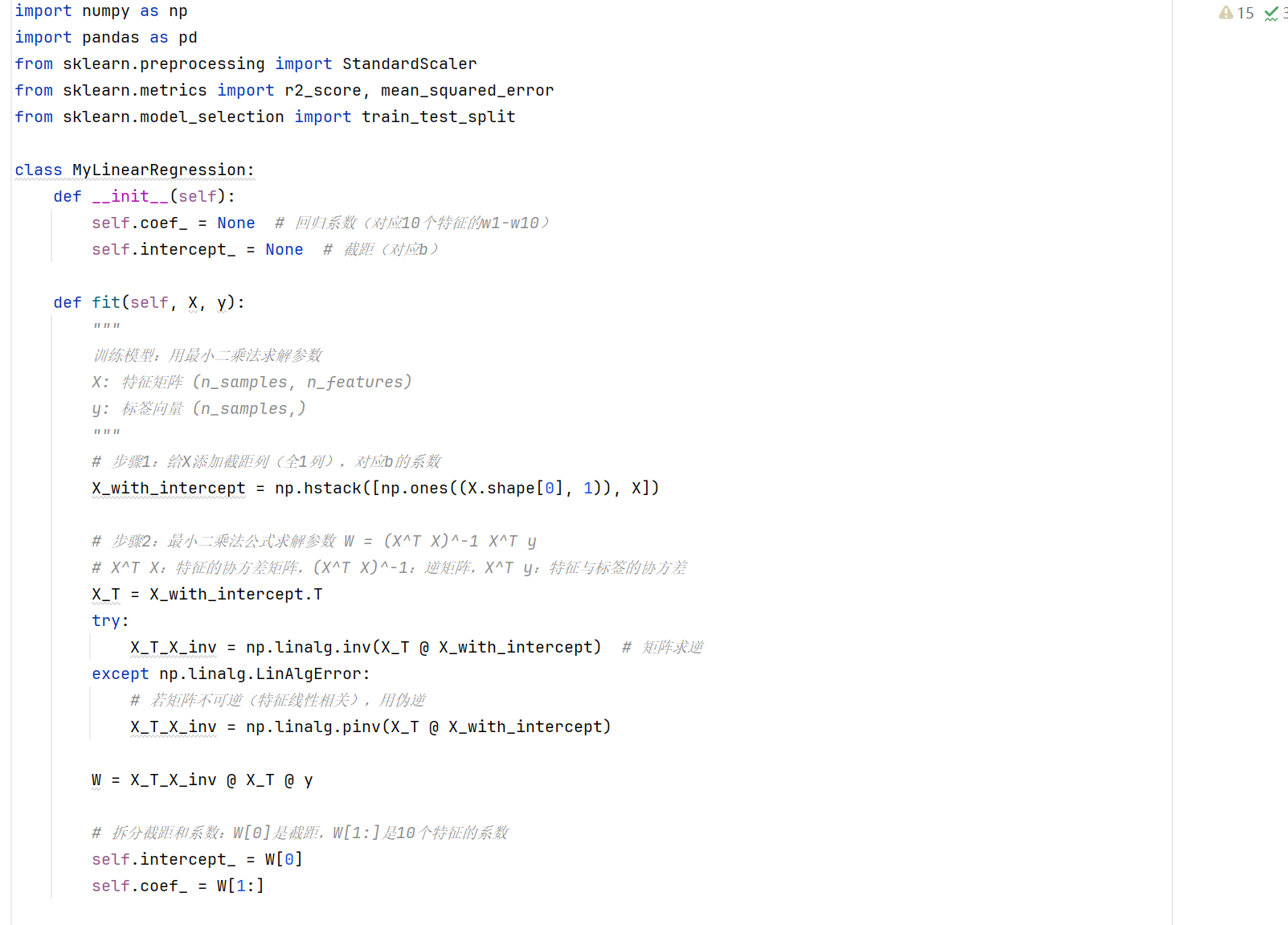
python
截距 b = 151.3457
特征1的系数 w1 = 1.8027
特征2的系数 w2 = -11.5092
特征3的系数 w3 = 25.8006
特征4的系数 w4 = 16.5388
特征5的系数 w5 = -44.3051
特征6的系数 w6 = 24.6408
特征7的系数 w7 = 7.7723
特征8的系数 w8 = 13.0952
特征9的系数 w9 = 35.0169
特征10的系数 w10 = 2.3150
=== 模型评估结果 ===
训练集 R² = 0.5279
训练集 MSE = 2868.5466
测试集 R² = 0.4526
测试集 MSE = 2900.1733
=== sklearn官方线性回归参数(对比验证) ===
截距 b = 151.3457
特征1的系数 w1 = 1.8027
特征2的系数 w2 = -11.5092
特征3的系数 w3 = 25.8006
特征4的系数 w4 = 16.5388
特征5的系数 w5 = -44.3051
特征6的系数 w6 = 24.6408
特征7的系数 w7 = 7.7723
特征8的系数 w8 = 13.0952
特征9的系数 w9 = 35.0169
特征10的系数 w10 = 2.3150
sklearn测试集 R² = 0.4526
Ridge测试集 R² = 0.4541