今日课程提纲 ：
接下来将介绍model-free control。就是当没法得到马尔科夫决策过程里面模型的情况下，如何去优化它的价值函数，如何去得到一个最佳的策略。这里我们将把之前我们介绍的policy iteration进行一个广义的推广，使它能够兼容MC和TD。
目录
- 二、Model-free
-
- [2.2 Model-free control](#2.2 Model-free control)
-
- [2.2.1 policy iteration回顾](#2.2.1 policy iteration回顾)
- [2.2.2 generalize policy iteration](#2.2.2 generalize policy iteration)
-
- [2.2.2.1 MC方法求q table](#2.2.2.1 MC方法求q table)
- [2.2.2.2 TD方法求q table](#2.2.2.2 TD方法求q table)
- 三、总结
- 四、代码
二、Model-free
2.2 Model-free control
2.2.1 policy iteration回顾
首先是一个policy iteration的复习，policy iteration由两部分组成。第一部分是通过一个迭代的过程去估计它的价值函数，就给定一个当前的policy π，然后估计它的价值函数。第二部分是我们得到了估计出来的价值函数过后，我们通过一个Greedy的办法去改进它的一个算法。所以这两个步骤是一个互相迭代的过程，我们逐渐就从初始化得到了一个最佳的v和跟π，就通过这个evaluation and improvement的互相迭代就逐渐改进。
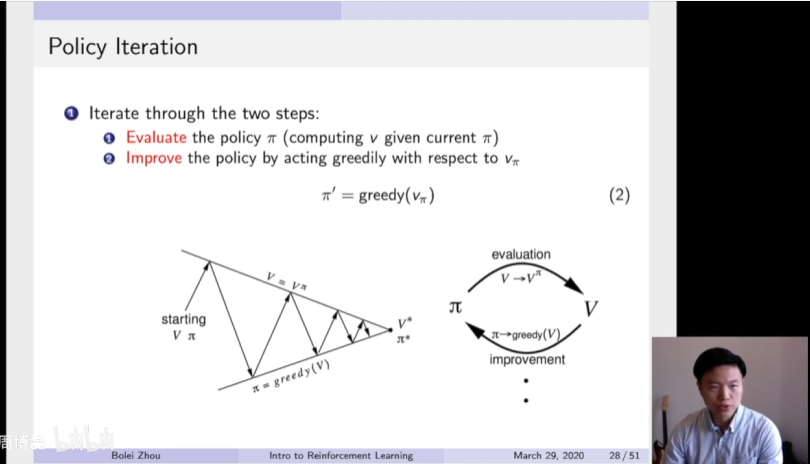
但是这里面临一个问题，得到了一个价值函数过后，并不知道它的奖励函数以及状态转移，所以就没法估计它的Q函数。所以一个问题是，当不知道奖励函数以及状态转移矩阵的时候，如何进行策略的一个优化。所以这里就有一个广义的generalize的policy的一个方法。
2.2.2 generalize policy iteration
2.2.2.1 MC方法求q table
根据这两个步骤，policy evaluation以及policy improvement，这里我们在第一部分里面可以直接把用MC的一个方法去替代之前的DP的方法去估计这个Q函数。当我们得到Q函数过后，就可以通过Greedy的一个办法去改进它。所以这里是用MC方法去估计Q函数的一个算法。
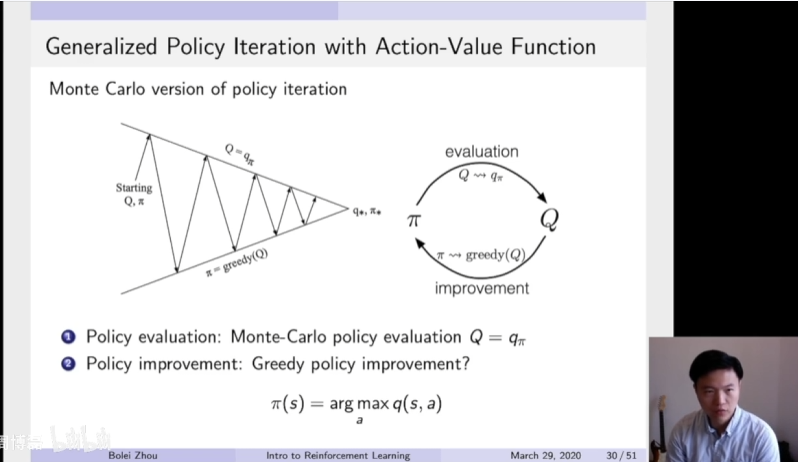
这里假设是我们的每一个episode都有一个exploring starts。因为这个exploring starts就类似于我们每一个步骤，每一个状态都希望能采样能采到。所以就需要这个exploring starts作为一个保证。就我们所有的action，所有的状态都可以在无限步的执行过后采到，这样我们才能很好的去估计。
这里是具体的一个算法，通过蒙特卡罗采样的方法产生很多轨迹，然后每一个轨迹都可以算得它的价值。这样得到过后，去通过这个average的一个方法去估计它的这个Q函数。因为这个Q函数可以把它看成一个table，就这个表格它的横轴是状态，纵轴是action。这样就通过采样的方法，把这个表格上面每一个单元都的值都填上。就通过这个mean average的一个办法然后填上。当得到这个表格过后，就可以通过第二步的这个policy improvement，然后去选取它的更好的一个策略。所以这里的核心就是如何利用MC方法去填这个q table这个表格。
这里就牵涉到一个怎么能确保MC算法能有足够的探索。所以这里面临一个trade off，就面临一个exploration跟exploitation的一个trade off。在第一节课我也给大家介绍了exploration and exploitation的trade off，是在强化学习里面非常核心的一个问题。因为强化学习的核心思想就是让他在这个环境里面探索，这样可以获得最佳的策略。所以面临一个问题是怎么能确保这个agent在环境里面有更多、更好的探索。一个比较简单的方法，使得它能确保足够的探索，算法叫做ε-Greedy Exploration。所以这个算法大致意思说在每一步选取策略的时候有ε概率。这个ε在开始的时候是比较大的，比如说80%逐渐，然后它可以减小，然后到20%或者10%。
所以每次它概率有ε，比如说20%的概率，它随机选取一个行为，另外有1-ε，另外有80%的概率，他会采取这个Greedy的策略。因为Greedy策略可以确保你获取足够的奖励。这个ε的概率可以确保你对这个不同的行为足够的探索，有更高的概率获取可以获得更高奖励的行为。
可以把这个ε-Greedy写成一个概率的表达形式。这个等式是确保我们加和它还是一个概率。进一步推导，当follow这个ε-Greedy policy的时候，整个它的Q函数以及它的价值函数是单调递增的。
这里我给了一个简单的一个提示，感兴趣的同学可以进一步推导。就是当用蒙特卡罗以及这个ε-Greedy探索这个形式的时候，我们可以确保它的这个价值函数是monotonic单调改进。
所以这里是一个ε-Greedy的一个简单的算法表示。
刚开始这个q table是随机初始化的。所以我们MC的这个核心就是利用当前的这个策略，然后对这个环境进行探索，然后得到了一个一些轨迹。得到这些轨迹过后，可以开始更新。通过他得到了的return，然后通过这个incremental mean的方法去更新它的这个q table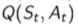
。q table里面有两个量，就是它的状态以及它的这个action，这样就可以估计出这个q table。当得到这个q table过后，进一步更新他的这个策略，就这个policy improvement，这样就可以得到下一阶段的这个策略
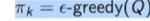。得到下一阶段的策略过后，又用更好的策略进行数据的采集。这样通过一个迭代的过程，就得到一个广义的一个policy iteration。
2.2.2.2 TD方法求q table
也可以把TD替代进去，因为MC是一种估计q table的方法，那么自然而然，也可以把TD这个方法估计进去。这里也是TD方法跟MC方法的一个对比，TD相对于MC来说的话，它的variance是比较低的。而且对于这个没有结束的游戏，已经可以开始更新它的这个q table，而且它可以处理不完整的序列。所以这里可以把TD也放到这个control loop里面去估计q table。然后再采取这个ε-Greedy的policy improvement。这样就可以在同一个episode没有结束的时候，就可以开始更新它已经采集到的状态。
接下来回忆一下TD prediction这个步骤。TD prediction给定了一个策略，然后去估计它的价值函数。所以这里采取的办法是TD(0) 的办法是根据当前策略，采取了一个行为，执行了这个行为，会观测到他的奖励以及进入到下一个状态。然后就可以构造出它的这个TD target，就是有它获取的奖励以及bootstrapping它下一步这个状态的值，然后作为它的TD target，然后更新它当前状态这个V(St)它的值。所以现在我们面临的问题是怎么把这个TD prediction的框架来估计它的这个action value function，就是它的这个q function。
1、on-policy TD control
Sarsa算法
所以我们这里有了这个on-policy TD control的一个算法，叫Sarsa。这个算法就是基于这个on-policy TD control。on-policy的意思是现在只有同一个policy，既利用这个policy来采集数据，这个policy也是我们优化的policy，所以这里只存在一个policy。为什么他名字叫Sarsa？
SARSA就是它这个过程，它需要采集到这种turbo，需要采集到有两个state，就是从你当前这个S开始。然后执行了一个action，就是第一个A然后会得到一个reward，然后会进入下一个状态。然后现在进一步执行一个action，这样就得到了第二个A所以他就缩写过来，所以就变成Sarsa这个词了。所以这个Sarsa算法也是跟TD prediction类似的，它是直接去估计这个q table，估计这个q table的话也是我们构造出这个TD target的，就是由它已经得到了这个reward以及bootstrapping他下一步要更新的这个Q，然后来更新它的当前这个q table的这个值。当我们得到这个q table过后，然后就可以进行采取它这个greedy的这个策略，更新它的这个策略。
这也是Sarsa具体的算法：刚开始初始化这个q table，现在开始基于当前这个策略，然后执行命令。先采样，通过当前的这个q table采样一个A，就得到了Sarsa里面的第一个A。我们采取这个action a然后会得到一个奖励以及这个S'。S'就是它的进入到下一个状态。现在我们有个A'，就是第二个A的出现。A'就是通过再一次我们通过这个策略，这个q table，然后来采样得到一个A'的行为。现在收集到所有的data过后，就既有了有了两个A以及两个S以及一个reward。然后我们就有了所有信息去更新这个q table的所有信息。更新过后，我们会往前走一步，所以当前这个状态S就会变成S'，然后当前这个action也会变成这个A'。这样就通过一步一步就可以进行迭代更新。
n step Sarsa算法
之前我们说了，可以把TD算法扩展它的步数，所以可以得到多个步的Sarsa，n step Sarsa算法，就通过调整它往前走的步数。比如说我们一步Sarsa，就是说我们得到往前走一步过后，然后就开始更新它的这个TD target。然后也可以有多步，比如说走两步，然后two step Sarsa，然后就是得到两个实际得到的奖励，然后再booststrapping它这个Q的价值，Q值，然后更新它的这个TD target。所以这里也可以进一步推广到N。到整个结束过后，那么它这个Sarsa算法就变成MC的这种更新的一个方法。当我们多步n step Sarsa update得到过后，就可以进行这个q table的更新。
2、off-policy TD control
另外off-policy learning的概念就是说在策略的学习过程中，可以保留两种不同的策略。第一个策略是进行优化的这个策略，希望学到一个最佳的策略。另外一个策略是拿来探索的这个策略。所以第二个策略因为它属于探索策略，就可以让它更激进的去对这个环境探索。所以这个off-policy learning的概念是说需要去学习这个策略，policy π。但是我们利用的数据采集到的trajectories是用第二个策略μ产生的。所以这里有两个策略，一个是这个policy π，就target policy是我们需要去学习的policy，policy μ是我们的行为policy。我们利用策略μ然后去采集轨迹，采集数据。利用采集到的这个数据，然后再喂给我们target policy进行学习。
一个容易理解的例子，你可以把它看成是这个学习的过程，就是这个环境是一个在海上波涛汹涌的环境。但是我们这里学习的这个learning policy，可能他自己太胆小了，他没法直接去跟这个环境进行学习。所以我们这里有了第二次behavior policy，它是一个可能无畏这个风浪的海盗，它非常激进。然后可以在这个环境里面实际去探索，然后产生了很多经验。他就会把他实际产生的这个经验写下来，写成这个稿子，然后喂给这个learning policy。所以就可以让这个胆小的这个policy通过这个behavior policy得到经验教训，然后来进行学习。这样他就不用直接跟这个环境进行交互。
所以在这个off-policy learning的过程中，这些观测轨迹都是通过policy μ跟环境进行交互产生的。当我们得到这些轨迹过后，让我们去update这个policy π，需要去学习的这个target policy。这样的off-policy操作有很多好处 ：
第一是可以学到最佳的策略，利用一个更激进的这exploratory policy，这样就会使得我们的学习效率也非常高。
第二则是这个框架是可以让我们学习其他意见的行为。就比如说我们采集到这些轨迹可能是人产生的。就通过模仿学习人的轨迹，这样我们可以学习，也可以是其他Agent产生的。
第三个好处是可以重用一些之前老的策略产生的轨迹。因为这一点是非常重要，因为在这个探索过程是需要消耗非常多的计算资源。需要很多计算机计算资源来做rollout（轨迹采样），产生这个轨迹。如果对于我们当前优化的，我们之前产生的轨迹不能利用的话，这样就浪费了很多资源。所以通过这个off-policy learning的方法，我们就可以使得之前比较老的这些轨迹产生的这些观测，产生的这些trajectory也可以继续存下来，然后继续用。这个思想也是我们下一次课或者下次课会介绍的这个deep Q-learning采取的思想。他就用一个replay buffer来包含之前比较老的轨迹产生的这些经验。然后我们带着这些老的经验进行采样，然后构建了新的training batch来更新我们的这个target policy。
Q-learning算法
所以这就是我们off policy Q-learning的算法。这里有两种policy，一种是behavior policy，另外一个是target policy。我们这里target policy π，就是说他直接利用他这个greedy，就直接让他在这个q table上面取他greedy是他的policy。所以对于某一个状态，那么它下一步的最佳策略就应该是这个arg max这个操作，就取它下一步可能得到所有状态。另外我们的这个behavior policy μ可以是一个随机的policy。
但是我们这里采取的是follow一个ε-Greedy，就让它这个behavior policy不至于它是完全随机的，它还是有些随机性。但是它也是基于我们这个q table组件在进行改进的，所以我们这里用ε-Greedy policy。所以我们这里看到有两种policy。一种是greedy policy以及另外一种是ε-Greedy policy。这两种policy在这个策略优化刚刚开始的时候是非常不同的。因为我们之前说过ε-Greedy可能是在刚刚开始的时候，这个ε值是非常大。它可能是百分之百或者90%的随机扰动，然后产生数据，然后再来学习。在训练，逐渐更接近收敛的时候，这个ε的值也会逐渐变小，变成10%。
所以这两个策略会在后期的时候是越来越像。当我们采取这个Q-learning的时候，就可以构造出它的这个Q-learning target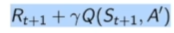
。Q-learning target就会使得现在每一步，它后面采取的这个策略都应该是这个arg max这个操作。所以我们直接把这个arg max代入进来，然后进行一个变化。然后就会把这个arg max这个值放到外面，然后就是直接是取的max这个值。所以就构建出了它当前的这个TD target，Q-learning的这个TD target的要优化的值
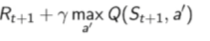。所以我们应该把Q-learning这个update写成这个incremental learning的形式。这个TD target就变成这个max这个值
。
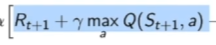所以这个是我们Q-learning的算法。你可以发现当我们采取当前的这个行为过后，choose a from s using policy derived from q这里我们就是follow这个ε-Greedy的这个policy，得到了当前的这个action。然后我们采取当前的action，然后观测到了reward S'。
这里跟Sarsa算法很重要的不同是，我们并没有采样第二个action。因为第二个action是需要我们构造这个TD target的，所以在Sarsa里面我们是需要去遵从我们的这个target policy去采样第二个A。但是在这个 Q-learning 里面我们并没有直接去采样。我们这里采取的操作是直接去看那个 Q-table，然后取它的这个 max 的值，这样就构造出了它的这个 TD target，然后就可以对它的这个 Q 值进行一个优化。然后优化过后，我们现在把进入下一步的这个 S 的状态，继续作为新的当前状态，重复同样的更新过程。
Q-learning跟Sarsa的对比
这里可以把Q-learning跟Sarsa进行一个对比。这里Sarsa算法是on-policy TD control，Q-learning是off-policy TD control。这两者虽然只有一些很非常细小的一个差别，但是会决定这个两种算法他的行为是完全不同的。
就对于Sarsa来说，你可以发现这里他有两个action，就At跟At+1。这两个action都是通过他的一个同一个policy，然后采样出来，采样出来过后，Q才能进行更新。但是对于Q-learning其实只执行了第一个action。比如说当前这个action At。然后是从他的behavior policy里面采样出来的。然后他当前的这个At+1其实是它并没有采取这个行为，是它imagine出来的。使得这个值org max，即这个值达到极大化的那个action，应该是他下一步的这个action。所以就构造出了它的这个TD target。
有这个max的Operator在这个TD target里面，然后进行这个incremental learning，然后去nudge这个Q所以这是Sarsa跟q turning两者非常不同的一个地方。
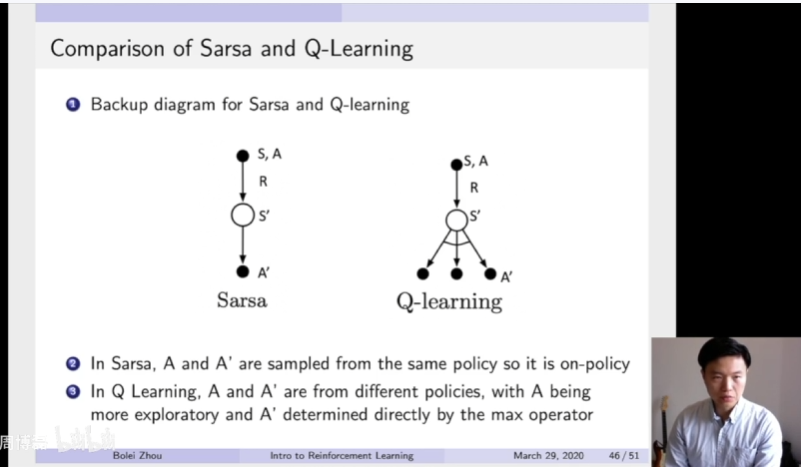
把这个backup diagram进行一个对比。Sarsa只有一条路，它通过构造出当前这个S然后采样出来这个A然后得到这个奖励，然后到达这个S'，然后再采样它的target policy，然后得到这个A'，就这样就可以构造出它的这个更新了。但是对于这个q-learning，它有了这个SA采样过后，然后产生这个reward，它的S'。然后它这里有个Operator，就是max Operator，就是采样他当前要去的这个max Operator，然后作为他的下一步最可能的这个action。所以它在Sarsa里面，A跟A'都是从同一个policy里面产生的，所以它是on-policy。但是在Q-learning里面，它的A跟A'它是从不同policy里面产生。所以A会更exploration，但A'是直接从这个max Operator里面执行产生。
这里我提供了一个简单的一个Cliff work一个环境，可以对比出Sarsa跟Q-learning的算法得出的不同。这个环境是在这个great world里面，这个agent需要从这个S的这个格子开始，然后到达这个G这个格子。然后这里它在这个格子里面可以上下左右移动，然后它得避免这个Cliff这几个格子。如果它进入这个Cliff的这个格子过后，它就会得到-100的奖励。然后他每走一步会有一个-1的奖励。所以这里Sarsa出来的结果，他得到的最佳轨迹，结果会跟Q-learning非常不同。
因为Sarsa是on-policy learning，所以他会采取一个非常保守的一个策略。因为他如果掉到这个悬崖下去过后，然后他就会得到很负的奖励。所以他整个策略的学习，他会倾向于一个非常保守的一个策略。所以你看他最后收敛过后，他得到的这个reward，你就左下角这个值，R就是它决定这个轨迹。
你可以发现这个Sarsa选出来的这个policy，它就是会逐渐往上走，就走到非常上面，然后再到下面，然后再走下来。这样使这个agent尽量远离这个Cliff的位置。但是这个Q-learning它学出来的会非常激进，然后去学出一个沿着这个悬崖边上走，最后到达这个G的位置。但是在这个环境里面，它最佳策略就是尽量靠近这个Cliff。所以这个Q-learning它会采取一个非常激进的学习策略，这样就会他学到最佳的策略。
右下角的learning curve里面，在学习的过程中，这个Q-learning它其实一直他的这个learning curve是相对于Sarsa是要更低的。因为他采取的这个策略是非常激进，他有一个behavior policy是非常随机去探索这个环境，所以他有更大的概率掉到这个悬崖下面去，所以他这个learning reward是相对比较低的。但是Sarsa会保证一个比较保守的一个策略，所以它的moving average会比这个Q-learning更高。但是当整个策略整个学习过程完成过后，我们得到这个最佳策略会发现Q-learning得到这个最佳策略会更接近于实际的最佳策略。然后我在这个code base里面也提供了一个code，大家可以实际去是运行这个代码。
三、总结
我们对于之前的这个policy iteration，如果是用dynamic programming，用动态规划的方法来执行的话，那么就直接policy evaluation也是算他这个期望。对这个Q-learning，q police iteration也是把这个期望带进去。然后value iteration也是这个过程，就算它的expectation。如果我们这里用TD的方法，就用sample base的方法，就会产生新的这个TD target。就会这个target就会有它实际得到的奖励，以及这个bootstripping产生的这个value价值进行一个更新。然后基于他的这个更新策略的不同，这个Sarsa是on-policy learning，所以他会直接去执行，到下一步来进行这个bootstripping的更新。但是Q-learning采取更激进的更新，所以它会把这个max Operator放到它的这个TD target里面去。然后我们就我看出了基于这个算法，就你是用DP或者TD然后会得到不同的target。
这就是我们第三次课的内容，做一个简单的总结。我们分析了model-free prediction，就如何在一个马尔科夫决策过程里面，我们并没有模型的时候怎么去估计它的价值函数。然后我们进一步把这个model-free prediction扩展到这个model-free control。就给定一个未知的一个马尔科夫决策过程，我们并没有他的知道它的奖励函数以及它的转移矩阵。怎么通过Sarsa算法以及Q-learning算法对他进行控制，获取它的最佳策略。
四、代码
这里我提供首先是提供了这个Cliff work的这个例子。我们首先来看一下这个play work的代码，这里我们这个代码它实现了Sarsa、Q-learning两种方法。对于Sarsa算法，这里只有一种ε-Greedy policy.
你发现我们这里先采取第一个action，然后第二个action是直接从这个采样采出来的，然后得到了这两个action过后，我们就可以开始构造这个TD target。这里就构造出了它的TD他给然后我们算它的这个TD error，然后再对它的这个Q值进行更新。所以这个Sarsa是比较容易理解的，就直接利用这样采样两次action，然后得到了它的reward，往前走一步过后然后进行更新。
我们再来看一下这个Q-learning，他这里第一个action是ε-Greedy产生的，然后他往前走了一步。这个跟Sarsa很不同的是走一步过后，他就可以通过bootstripping去看这个q table上面谁是max的这个值，然后就构造出他当前的这个TD target。有了当前的TD target过后，然后他就可以立刻去更新它的这个q value的值了。它并不需要去执行第二个action，所以这样然后它再更新它的这个state，进入到下一个state，让我们实际来运行一下这个带这他会可视化出他最后学习的这个pass。然后第一个轨迹它出现的是这个Q-learning出来的，你看它沿着这个悬崖走。然后第二个是他的Sarsa出来的轨迹，它就会远离他的这个悬崖，这样就会得到一个更保守这个sharp optimal的一个策略。
python
# Example 6.6 Cliff Walking in Chapter 6: Temporal Difference Learning in Sutton and Barto Textbook
# 这是Sutton和Barto强化学习教材第6章的悬崖行走问题示例
import matplotlib.pyplot as plt # 导入matplotlib用于可视化
import numpy as np # 导入numpy用于数值计算
from matplotlib.colors import hsv_to_rgb # 导入HSV到RGB的颜色转换函数
def change_range(values, vmin=0, vmax=1):
"""
将数值范围归一化到指定的最小值和最大值之间
用于将Q值映射到颜色强度范围
"""
start_zero = values - np.min(values) # 将最小值平移到0
# 归一化到[0,1]，然后映射到[vmin, vmax]
return (start_zero / (np.max(start_zero) + 1e-7)) * (vmax - vmin) + vmin
class GridWorld:
"""
网格世界环境类
实现了一个4x12的网格世界，其中包含正常区域、悬崖和目标
"""
# 定义不同地形的颜色（HSV格式）
terrain_color = dict(normal=[127 / 360, 0, 96 / 100], # 正常区域：灰色
objective=[26 / 360, 100 / 100, 100 / 100], # 目标：黄色
cliff=[247 / 360, 92 / 100, 70 / 100], # 悬崖：蓝色
player=[344 / 360, 93 / 100, 100 / 100]) # 玩家：粉红色
def __init__(self):
"""初始化网格世界"""
self.player = None # 玩家位置初始化为None
self._create_grid() # 创建网格
self._draw_grid() # 绘制网格
self.num_steps = 0 # 步数计数器
def _create_grid(self, initial_grid=None):
"""创建4x12的网格，初始化所有格子为正常地形"""
self.grid = self.terrain_color['normal'] * np.ones((4, 12, 3))
self._add_objectives(self.grid) # 添加悬崖和目标
def _add_objectives(self, grid):
"""
添加特殊地形：
- 最后一行的第2到第11列设置为悬崖
- 最后一行最后一列设置为目标
"""
grid[-1, 1:11] = self.terrain_color['cliff'] # 悬崖区域
grid[-1, -1] = self.terrain_color['objective'] # 目标位置
def _draw_grid(self):
"""初始化matplotlib图形用于可视化"""
self.fig, self.ax = plt.subplots(figsize=(12, 4)) # 创建图形
self.ax.grid(which='minor') # 显示次要网格线
# 为每个格子创建文本对象，用于显示Q值
self.q_texts = [self.ax.text(*self._id_to_position(i)[::-1], '0',
fontsize=11, verticalalignment='center',
horizontalalignment='center') for i in range(12 * 4)]
# 显示网格图像
self.im = self.ax.imshow(hsv_to_rgb(self.grid), cmap='terrain',
interpolation='nearest', vmin=0, vmax=1)
# 设置主刻度和次刻度
self.ax.set_xticks(np.arange(12))
self.ax.set_xticks(np.arange(12) - 0.5, minor=True)
self.ax.set_yticks(np.arange(4))
self.ax.set_yticks(np.arange(4) - 0.5, minor=True)
def reset(self):
"""
重置环境到初始状态
返回：初始状态的ID
"""
self.player = (3, 0) # 玩家从左下角开始
self.num_steps = 0 # 重置步数
return self._position_to_id(self.player) # 返回状态ID
def step(self, action):
"""
执行一个动作，返回新状态、奖励和是否结束
参数：
action: 0=上, 1=下, 2=右, 3=左
返回：
next_state: 新状态的ID
reward: 获得的奖励
done: 是否到达终止状态
"""
# 根据动作更新玩家位置（带边界检查）
if action == 0 and self.player[0] > 0: # 向上移动
self.player = (self.player[0] - 1, self.player[1])
if action == 1 and self.player[0] < 3: # 向下移动
self.player = (self.player[0] + 1, self.player[1])
if action == 2 and self.player[1] < 11: # 向右移动
self.player = (self.player[0], self.player[1] + 1)
if action == 3 and self.player[1] > 0: # 向左移动
self.player = (self.player[0], self.player[1] - 1)
self.num_steps = self.num_steps + 1 # 增加步数计数
# 根据新位置确定奖励和是否结束
if all(self.grid[self.player] == self.terrain_color['cliff']):
# 掉入悬崖：大负奖励，回合结束
reward = -100
done = True
elif all(self.grid[self.player] == self.terrain_color['objective']):
# 到达目标：0奖励，回合结束
reward = 0
done = True
else:
# 正常移动：小负奖励（鼓励快速到达目标），继续
reward = -1
done = False
return self._position_to_id(self.player), reward, done
def _position_to_id(self, pos):
"""将二维坐标(行,列)映射到唯一的状态ID"""
return pos[0] * 12 + pos[1]
def _id_to_position(self, idx):
"""将状态ID映射回二维坐标(行,列)"""
return (idx // 12), (idx % 12)
def render(self, q_values=None, action=None, max_q=False, colorize_q=False):
"""
渲染当前环境状态
参数：
q_values: Q值表，用于显示
action: 当前执行的动作
max_q: 是否只显示最大Q值
colorize_q: 是否用颜色编码Q值
"""
assert self.player is not None, 'You first need to call .reset()'
if colorize_q:
# 使用Q值的颜色编码来显示网格
assert q_values is not None, 'q_values must not be None for using colorize_q'
grid = self.terrain_color['normal'] * np.ones((4, 12, 3))
# 将每个状态的最大Q值映射到颜色饱和度
values = change_range(np.max(q_values, -1)).reshape(4, 12)
grid[:, :, 1] = values # 修改饱和度通道
self._add_objectives(grid) # 重新添加悬崖和目标
else:
grid = self.grid.copy()
# 在网格上标记玩家位置
grid[self.player] = self.terrain_color['player']
self.im.set_data(hsv_to_rgb(grid))
if q_values is not None:
xs = np.repeat(np.arange(12), 4) # x坐标
ys = np.tile(np.arange(4), 12) # y坐标
# 更新每个格子的Q值文本
for i, text in enumerate(self.q_texts):
if max_q:
# 只显示最大Q值
q = max(q_values[i])
txt = '{:.2f}'.format(q)
text.set_text(txt)
else:
# 显示所有动作的Q值
actions = ['U', 'D', 'R', 'L']
txt = '\n'.join(['{}: {:.2f}'.format(k, q) for k, q in zip(actions, q_values[i])])
text.set_text(txt)
if action is not None:
# 在标题中显示当前动作
self.ax.set_title(action, color='r', weight='bold', fontsize=32)
plt.pause(0.01) # 短暂暂停以更新显示
def egreedy_policy(q_values, state, epsilon=0.1):
"""
ε-贪婪策略：用于平衡探索和利用
参数：
q_values: Q值表
state: 当前状态
epsilon: 探索概率
返回：
选择的动作
工作原理：
- 以ε概率随机选择动作（探索）
- 以1-ε概率选择Q值最大的动作（利用）
"""
if np.random.random() < epsilon:
return np.random.choice(4) # 随机探索
else:
return np.argmax(q_values[state]) # 贪婪利用
def q_learning(env, num_episodes=500, render=True, exploration_rate=0.1,
learning_rate=0.5, gamma=0.9):
"""
Q-Learning算法：Off-policy TD控制算法
核心思想：使用目标策略（贪婪）来更新Q值，但使用行为策略（ε-贪婪）来选择动作
参数：
env: 环境对象
num_episodes: 训练回合数
render: 是否可视化
exploration_rate: 探索率ε
learning_rate: 学习率α
gamma: 折扣因子γ
返回：
ep_rewards: 每个回合的总奖励
q_values: 学习到的Q值表
"""
# 初始化Q值表为全0
q_values = np.zeros((num_states, num_actions))
ep_rewards = [] # 记录每个回合的奖励
for _ in range(num_episodes):
state = env.reset() # 重置环境，获取初始状态
done = False
reward_sum = 0 # 累计奖励
while not done:
# 【步骤1】使用ε-贪婪策略选择动作（行为策略）
action = egreedy_policy(q_values, state, exploration_rate)
# 【步骤2】执行动作，观察奖励和新状态
next_state, reward, done = env.step(action)
reward_sum += reward
# 【步骤3】Q-Learning更新公式（核心）
# TD目标 = r + γ * max_a Q(s', a) <- 使用贪婪策略（目标策略）
td_target = reward + 0.9 * np.max(q_values[next_state])
# TD误差 = TD目标 - 当前Q值
td_error = td_target - q_values[state][action]
# 更新Q值：Q(s,a) <- Q(s,a) + α * TD误差
q_values[state][action] += learning_rate * td_error
# 【步骤4】转移到下一个状态
state = next_state
if render:
env.render(q_values, action=actions[action], colorize_q=True)
ep_rewards.append(reward_sum) # 记录本回合总奖励
return ep_rewards, q_values
def sarsa(env, num_episodes=500, render=True, exploration_rate=0.1,
learning_rate=0.5, gamma=0.9):
"""
SARSA算法：On-policy TD控制算法
核心思想：使用实际执行的动作来更新Q值（行为策略和目标策略相同）
参数：
env: 环境对象
num_episodes: 训练回合数
render: 是否可视化
exploration_rate: 探索率ε
learning_rate: 学习率α
gamma: 折扣因子γ
返回：
ep_rewards: 每个回合的总奖励
q_values_sarsa: 学习到的Q值表
与Q-Learning的区别：
- Q-Learning: TD目标使用max Q(s',a') (贪婪)
- SARSA: TD目标使用实际选择的Q(s',a') (ε-贪婪)
"""
# 初始化Q值表为全0
q_values_sarsa = np.zeros((num_states, num_actions))
ep_rewards = [] # 记录每个回合的奖励
for _ in range(num_episodes):
state = env.reset() # 重置环境
done = False
reward_sum = 0
# 【步骤1】使用ε-贪婪策略选择初始动作
action = egreedy_policy(q_values_sarsa, state, exploration_rate)
while not done:
# 【步骤2】执行动作，观察奖励和新状态
next_state, reward, done = env.step(action)
reward_sum += reward
# 【步骤3】为下一个状态选择动作（使用相同的ε-贪婪策略）
next_action = egreedy_policy(q_values_sarsa, next_state, exploration_rate)
# 【步骤4】SARSA更新公式（核心）
# TD目标 = r + γ * Q(s', a') <- 使用实际要执行的动作a'
td_target = reward + gamma * q_values_sarsa[next_state][next_action]
# TD误差 = TD目标 - 当前Q值
td_error = td_target - q_values_sarsa[state][action]
# 更新Q值：Q(s,a) <- Q(s,a) + α * TD误差
q_values_sarsa[state][action] += learning_rate * td_error
# 【步骤5】更新状态和动作（S, A, R, S', A' 五元组）
state = next_state
action = next_action # SARSA的关键：使用已选择的下一个动作
if render:
env.render(q_values, action=actions[action], colorize_q=True)
ep_rewards.append(reward_sum) # 记录本回合总奖励
return ep_rewards, q_values_sarsa
def play(q_values):
"""
使用学习到的Q值表来演示一个完整回合
采用完全贪婪策略（ε=0）
"""
# 创建新环境实例
env = GridWorld()
state = env.reset() # 重置到初始状态
done = False
while not done:
# 使用贪婪策略选择动作（不再探索）
action = egreedy_policy(q_values, state, 0.0)
# 执行动作
next_state, reward, done = env.step(action)
# 更新状态
state = next_state
# 可视化
env.render(q_values=q_values, action=actions[action], colorize_q=True)
# ==================== 主程序 ====================
# 定义动作常量
UP = 0
DOWN = 1
RIGHT = 2
LEFT = 3
actions = ['UP', 'DOWN', 'RIGHT', 'LEFT']
### 创建环境
env = GridWorld()
num_states = 4 * 12 # 状态空间大小：4行 × 12列 = 48个状态
num_actions = 4 # 动作空间大小：上、下、右、左
### 使用Q-Learning训练
print("=== 训练Q-Learning ===")
# 训练单次，gamma=0.9, learning_rate=1
q_learning_rewards, q_values = q_learning(env, gamma=0.9, learning_rate=1, render=False)
env.render(q_values, colorize_q=True) # 可视化最终的Q值
# 运行10次实验取平均，评估性能稳定性
q_learning_rewards, _ = zip(*[q_learning(env, render=False, exploration_rate=0.1,
learning_rate=1) for _ in range(10)])
avg_rewards = np.mean(q_learning_rewards, axis=0) # 计算平均奖励
mean_reward = [np.mean(avg_rewards)] * len(avg_rewards) # 总平均奖励
# 绘制Q-Learning的学习曲线
fig, ax = plt.subplots()
ax.set_xlabel('Episodes using Q-learning')
ax.set_ylabel('Rewards')
ax.plot(avg_rewards) # 每个回合的平均奖励
ax.plot(mean_reward, 'g--') # 总体平均奖励（绿色虚线）
print('Mean Reward using Q-Learning: {}'.format(mean_reward[0]))
### 使用SARSA训练
print("\n=== 训练SARSA ===")
# 训练单次，learning_rate=0.5, gamma=0.99
sarsa_rewards, q_values_sarsa = sarsa(env, render=False, learning_rate=0.5, gamma=0.99)
# 运行10次实验取平均
sarsa_rewards, _ = zip(*[sarsa(env, render=False, exploration_rate=0.2) for _ in range(10)])
avg_rewards = np.mean(sarsa_rewards, axis=0)
mean_reward = [np.mean(avg_rewards)] * len(avg_rewards)
# 绘制SARSA的学习曲线
fig, ax = plt.subplots()
ax.set_xlabel('Episodes using Sarsa')
ax.set_ylabel('Rewards')
ax.plot(avg_rewards)
ax.plot(mean_reward, 'g--')
print('Mean Reward using Sarsa: {}'.format(mean_reward[0]))
# 可视化推理阶段的表现
print("\n=== Q-Learning策略演示 ===")
play(q_values) # 使用Q-Learning学到的策略
print("\n=== SARSA策略演示 ===")
play(q_values_sarsa) # 使用SARSA学到的策略