来源《深度强化学习实践》机械工业出版社，读书笔记和总结
目录
一、价值、状态和最优性
1、价值
价值定义：从状态获得的预期的总奖励
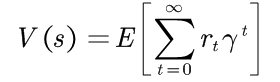
其中，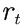
是片段t获得的奖励，
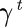是折扣因子。
2、价值计算
- 环境1下：
（1）智能体的初始状态；
（2）智能体从初始状态执行动作"向右"后，达到最终状态，获得奖励1；
（3）智能体从初始状态执行动作"向下"后，达到最终状态，获得奖励2.
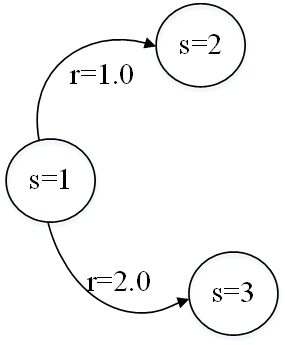
环境始终确定，每个动作都可以成功，并且我们总从状态1开始。一旦到达状态2或者3就结束。那状态1的价值是多少？如果没有智能体的行为或者策略信息，这个问题就毫无意义。即使在简单的环境中，智能体也可以有无数种行为，对于状态1每种状态都有自己的价值。考虑如下策略：
（1）智能体始终向右；
（2）智能体始终向下；
（3）智能体以0.5概况向右，以0.5概率向下；
（4）智能体以0.1概况向右，以0.9概率向下；
那么计算价值如下：
（1）智能体始终向右,状态1的价值为=1.0；
（2）智能体始终向下，状态1的价值为=2.0；
（3）智能体以0.5概况向右，以0.5概率向下，状态1的价值为=0.5*1.0+0.5*2.0=1.5；
（4）智能体以0.1概况向右，以0.9概率向下，状态1的价值为=0.1*1.0+0.9*2.0=1.9；
对于这个单步环境，总奖励等于状态1的价值，选择策略2总奖励最大。
- 环境2下：
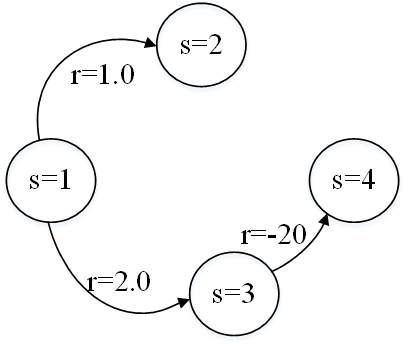
增加状态3到状态4后才终止
那么计算价值如下：
（1）智能体始终向右,状态1的价值为=1.0；
（2）智能体始终向下，状态1的价值为=2.0+（-20.0)=-18.0；
（3）智能体以0.5概况向右，以0.5概率向下，状态1的价值为=0.5*1.0+0.5*(-18.0)=-8.5；
（4）智能体以0.1概况向右，以0.9概率向下，状态1的价值为=0.1*1.0+0.9*(-18.0)=-16.1；
对于环境2，总奖励选择策略1时最大。
3、最优性
状态的最优价值，等于状态下动作的总奖励的最大值
二、最佳Bellman方程
1、初始状态可到达N个状态的抽象环境
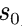和N个可用动作，每个动作会进入另一个状态
，并带有相应的奖励
，连接到状态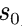的所有状态价值为
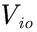，智能体可以采取的最佳动作方案是什么？
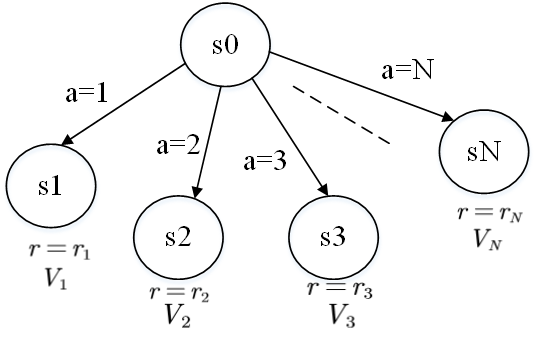
选择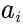
动作的价值为：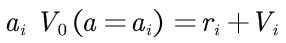
最佳动作方案选择，即确定性情况下最佳Bellman方程：
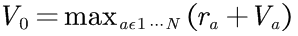
使用折扣因子：
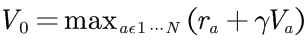
贪婪采取动作，采取立即奖励+状态长期奖励价值。
2、初始状态随机转移到其他状态
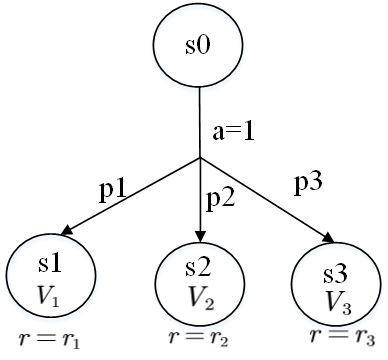
一个动作会以不同的概率导致三种不同的结果状态。以p1到达状态s1,以p2到达状态s2,以p3到达状态s3(p1+p2+p3=1)，每个目标状态的奖励为r1、r2、r3，计算执行动作1后的期望价值，需要将各个状态的价值乘以概率后相加：
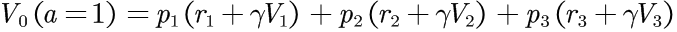
或者：
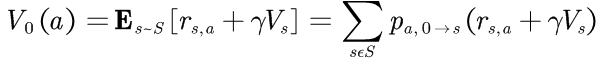
**3、**Bellman方程
通过确定性情况下的Bellman方程和随机动作的价值组合，可以得到一般情况下的Bellman最优方程：
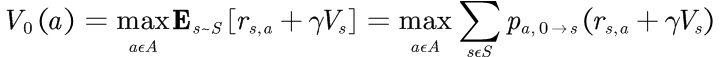
其中，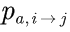
表示从状态i，执行动作a到状态j的概率。
- 状态最优价值等于动作所获得最大预期的立即奖励，再加上下一状态的长期折扣奖励。定义是递归的：状态的价值是通过立即可达到状态的价值来定义的。
- 获得奖励的最佳策略：假设每个状态的价值已知，那么将知道如何获得所有这些奖励。
- Bellman最优性证明，智能体在每个状态都选择能获得最佳奖励的动作，该奖励就是立即奖励与单步折扣长期奖励之和。
三、动作价值
1、动作价值定义
Q(s,a)定义不同的动作价值，其等于在状态s时执行动作a可获得的总奖励，并且可通过状态价值V(s)进行定义。比起V(s)，Q(s,a)更加方便使用，因此该变量的整个家族方法起名为Q-learning.获取每个状态和动作的Q值：
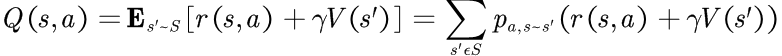
Q等于在状态s时采取动作a所预期获得的立即奖励和目标状态折扣长期奖励之和。可以通过Q(s,a)定义V(s)：
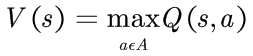
某些状态的价值等于从该状态执行某动作能获得的最大价值，用递归的方式表示Q(s,a):
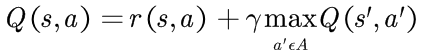
2、网格环境案例
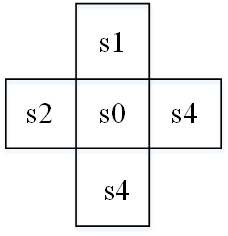
简化网格状环境
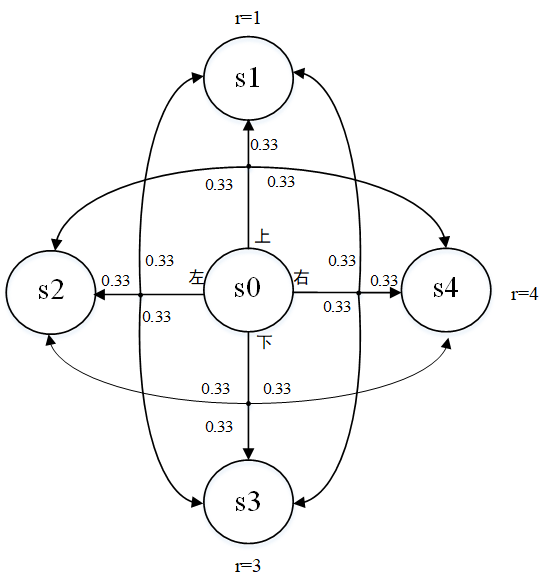
网格环境转移图
每个动作的概率都与FrozenLake（某游戏）中方式相同：33%的概率会按动作执行，33%的概率会滑动到方向的左侧目标单元格，33%的概率会滑动到方向的右侧目标单元格，为简单起见假设=1.
首先计算一下开始动作的价值。最终状态s1、s2、s3和s4没有外向连接，因此对于所有动作，这些状态的Q为零。因此，最终状态的价值等于其立即奖励（一旦达到目的地，片段结束，没有任何后续状态）：V1=1,V2=2，V3=3,V4=4.即最终状态的价值.
状态0的动作价值要复杂一些。首先计算动作"上"的价值。根据定义，其价值等于立即奖励加上后续步骤的长期价值。对于动作"上"的任何可能的转移都没有后续步骤：
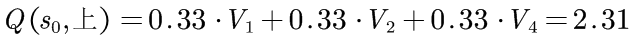
对于S0的其他动作重复上述计算：
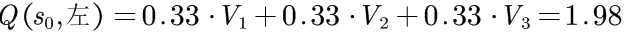
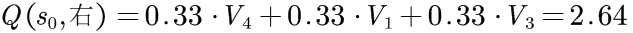
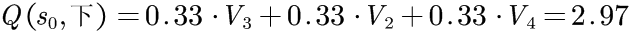
状态S0的最终价值为这些动作的最大价值，即2.97.
在实践中，Q值要更方便，对于智能体而言，制定决策时基于Q要比基于V简单。
对于Q而言，要基于状态选择动作，智能体只需要基于当前状态计算所以动作的Q值，并且选择Q值最大的动作即可。
对于V而言，智能体不仅要知道价值，还需要知道转移概率，在实践中我们很少能知道它们，所以智能体需要估计状态动作对的转移概率。
四、价值迭代法
1、包含循环的环境案例
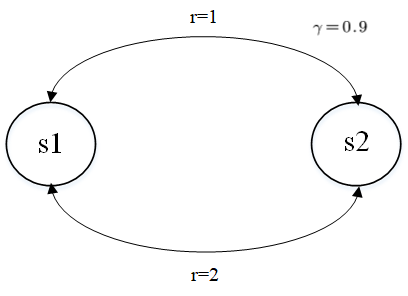
转移图包含循环的环境案例
状态的价值：
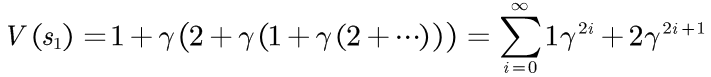
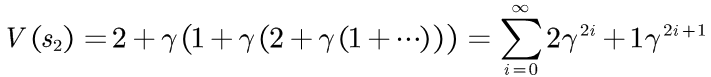
随之时间推移，每次转移的贡献值因为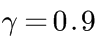
会减少，在50次迭代后，，
.
2、状态价值和动作价值计算
我们以数值计算已知状态转移概率和奖励值的马尔可夫决策过程（Markov Decision Process,MDP)的状态价值和动作价值。该过程状态价值包括如下步骤：
1）将所有状态的价值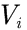
初始化为某个值（通常为0）；
2）对MDP中的每个状态s,执行Bellman更新：
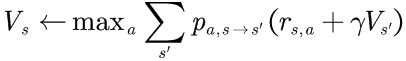
3）对许多步骤重复步骤2，或者直到更改变得很小为止。
对于动作价值（即Q)，只需要对前面的过程进行较小的修改即可：
1）将每个动作价值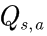
初始化为0；
2）对每个状态s和动作a执行以下更新：
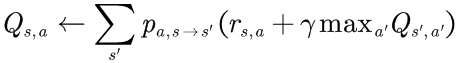
3）对许多步骤重复步骤2。
实际中，此方法有两个明显局限：
其一，状态空间必须是离散且足够小，以便对所有状态执行多次迭代。一个解决方案是离散化观察值，例如将CartPole的观察空间划分为多个箱体，但便产生了新问题，如应该用多大的间隔来划分箱体、需要多少环境数据来估计价值。（后续通过Q-learning中使用神经网络时解答）
其二，对于动作转移概率和奖励矩阵很少能得知。在Gym所提供的环境中，给智能体的接口为：观察状态、决定动作，然后才能获取下一个观察值以及转移奖励。在不查看Gym源码的情况下，从状态s0采取动作a0进入状态s1的概率是多少并不知道。
最后，在智能体与环境互动的过程中，我们仅仅拥有这些互动历史记录。在Bellman方程中，需要知道每个转移概率、转移奖励，因此需要通过互动历史记录经验来估计这两个未知值。关于奖励，记录从s0采取动作a转移到s1所获得奖励，可估计转移奖励；估计转移概率需要记录（s0,s1，a)元组，维护一个计数器并将其标准化。
五、价值迭代实践
1、数据结构
在本示例中，数据结构如下：
- 奖励表：记录奖励转移字典，键值(源状态，动作，目标状态），值为立即奖励。
- 转移表：记录动作转移字典，键值(状态，动作)，值为另一个字典，值字典是所观察到的目标状态和次数映射。例如，如果在状态0中，执行1动作十次，其中有三次进入状态4，七次进入状态5，则该表的键值为（0，1），值为{4:7,5,7}。通过该表来估计转移概率。
- 价值表：在v_iteration中，将（状态）映射到计算出的该状态的价值字典；在q_iteration中，将（状态,动作）映射到计算的价值字典.
2、环境要求
强化学习环境搭建如下：
|-------|-------------------------|----------------------------------|
| 序号 | 环境版本 | 环境介绍 |
| 1 | atari-py==0.2.6 | 提供Atari游戏环境的Python接口，用于强化学习研究 |
| 2 | gym=0.15.3 | OpenAI的强化学习环境库，包含各种标准测试环境 |
| 3 | numpy==1.17.2 | Python科学计算基础库，提供多维数组和数学函数 |
| 4 | opencv-python==4.1.1.26 | 计算机视觉库，用于图像和视频处理 |
| 5 | tensorboard==2.0.1 | TensorFlow的可视化工具，用于训练过程监控 |
| 6 | torch==1.3.0 | PyTorch深度学习框架的核心库 |
| 7 | torchvision==0.4.1 | PyTorch的计算机视觉扩展库，提供数据集和模型 |
| 8 | pytorch-ignite=0.2.1 | 简化PyTorch训练流程的高层库 |
| 9 | tensorboardX==1.9 | 让PyTorch等框架也能使用TensorBoard的库 |
| 10 | tensorflow==2.0.0 | Google的深度学习框架，2.0版本有重大API变化 |
| 11 | ptan==0.6 | PyTorch强化学习工具包，提供常用算法实现 |
(PS：加粗部分为本例需要的库）
3、实现
（1）v_iteration
a、代码实现
python
#!/usr/bin/env python3.7
import gym
import collections
from tensorboardX import SummaryWriter
ENV_NAME = "FrozenLake-v0"
#ENV_NAME = "FrozenLake8x8-v0" # uncomment for larger version
GAMMA = 0.9
TEST_EPISODES = 20
class Agent:
"""
基于模型的强化学习代理，使用动态规划（价值迭代）方法，学习方法如下：
1. 收集环境动态的随机经验（蒙特卡洛采样）
2. 构建环境的转移模型（转移表和奖励表）
3. 使用价值迭代算法计算最优状态价值
4. 根据最优价值函数选择动作
属性：
env: Gym环境实例
state: 当前环境状态
rewards: 奖励表，记录(state, action, next_state)的即时奖励
transits: 转移表，记录(state, action)转移到各next_state的次数
values: 状态价值表，记录每个状态的最优价值估计
方法：
play_n_random_steps: 执行随机步骤收集环境动态
calc_action_value: 计算状态-动作对的期望价值（Q值）
select_action: 选择当前状态下的最优动作
play_episode: 使用当前策略执行一个完整的情节
value_iteration: 执行价值迭代算法更新状态价值
"""
def __init__(self):
"""
初始化代理。
创建Gym环境实例，并初始化经验表和价值表。
"""
self.env = gym.make(ENV_NAME) # 创建Gym环境
self.state = self.env.reset() #获取第一个观察结果
self.rewards = collections.defaultdict(float)#奖励表：R(s,a,s')
self.transits = collections.defaultdict(
collections.Counter)#定义转移表：P(s'|s,a)的计数
self.values = collections.defaultdict(float)# 状态价值表：V(s)
def play_n_random_steps(self, count):
"""
执行随机步骤以收集环境动态信息（蒙特卡洛探索）。
通过随机动作收集状态转移和奖励信息，用于构建环境模型。
输入：count: 要执行的随机步骤数量
流程：
1. 随机选择动作
2. 执行动作，观察新状态和奖励
3. 记录奖励和状态转移
4. 如果情节结束则重置环境
"""
for _ in range(count):
action = self.env.action_space.sample() #随机选择一个动作
new_state, reward, is_done, _ = self.env.step(action) #执行动作
# 记录奖励：状态-动作-新状态 对应的奖励
self.rewards[(self.state, action, new_state)] = reward
# 记录状态转移：状态-动作 从(state, action)转移到new_state的次数
self.transits[(self.state, action)][new_state] += 1
# 更新当前状态（如果情节结束则重置环境）
self.state = self.env.reset() \
if is_done else new_state
def calc_action_value(self, state, action):
"""
计算状态-动作对的期望价值（Q值）。
根据贝尔曼方程计算：Q(s,a) = Σ_{s'} P(s'|s,a)[R(s,a,s') + γV(s')]
输入：state: 当前状态
action: 要评估的动作
输出：action_value: 动作价值的估计值
流程：
1. 获取从(state, action)转移的所有可能目标状态及其计数
2. 计算转移概率 = 计数/总计数
3. 对每个目标状态计算：即时奖励 + γ * 目标状态价值
4. 用转移概率加权求和得到期望价值
"""
# 获取从 (state, action) 转移到各目标状态的次数统计
target_counts = self.transits[(state, action)]
total = sum(target_counts.values())# 计算总转移次数
action_value = 0.0# 初始化动作价值
# 遍历所有可能转移到的目标状态
for tgt_state, count in target_counts.items():
# 获取即时奖励 R(s,a,s')
reward = self.rewards[(state, action, tgt_state)]
# 计算该转移的回报：即时奖励 + 折扣因子 * 下一状态价值
val = reward + GAMMA * self.values[tgt_state]
# 例如：reward=1.0, GAMMA=0.9, self.values[tgt_state]=0.5
# 则 val = 1.0 + 0.9*0.5 = 1.45
action_value += (count / total) * val# 用转移概率加权累加
# 假设 count/total = 0.5, val=1.45
# 则 action_value += 0.5 * 1.45 = 0.725
return action_value
def select_action(self, state):
"""
使用贪心策略选择当前状态下的最优动作。
1、对环境中所有动作进行迭代并计算每个动作的价值
2、动作价值最大的被返回
输入：当前状态 state
输出：最优动作 best_action
流程：
1. 初始化 best_action = None, best_value = None
2. 对于每个可能的动作 action：
a. 计算动作价值 Q(state, action)
b. 如果这是第一个动作，或价值更高：
更新 best_value = action_value
更新 best_action = action
3. 返回 best_action
"""
best_action, best_value = None, None
for action in range(self.env.action_space.n):
action_value = self.calc_action_value(state, action)
if best_value is None or best_value < action_value:
best_value = action_value
best_action = action
return best_action
def play_episode(self, env):
"""
基于模型的策略执行和模型学习函数
使用当前策略执行一个完整的情节，并更新环境模型。
输入：环境 env
输出：总奖励 total_reward
1. 初始化 total_reward = 0
2. 重置环境，获取初始状态 state
3. While True:
a. 根据当前状态选择动作 action = select_action(state)
b. 执行动作，得到新状态、奖励、完成标志
c. 记录奖励：rewards[(state, action, new_state)] = reward
d. 记录转移：transits[(state, action)][new_state] += 1
e. 累加奖励：total_reward += reward
f. 如果完成：break
g. 否则：更新状态 state = new_state
4. 返回 total_reward
"""
total_reward = 0.0
state = env.reset()
while True:
action = self.select_action(state)
new_state, reward, is_done, _ = env.step(action)
self.rewards[(state, action, new_state)] = reward
self.transits[(state, action)][new_state] += 1
total_reward += reward
if is_done:
break
state = new_state
return total_reward
def value_iteration(self):
"""
价值迭代算法 实现
根据贝尔曼最优方程更新状态价值：V(s) = max_a Σ_{s'} P(s'|s,a)[R(s,a,s') + γV(s')]
1、循环遍历环境中所有状态
2、为每个该状态可达到的状态计算价值,从而实现状态价值的候选项
3、用状态可执行动作的最大价值来更新当前状态的价值
"""
for state in range(self.env.observation_space.n):
# 计算所有动作的价值
state_values = [
self.calc_action_value(state, action)
for action in range(self.env.action_space.n)
]
# 更新为最大动作价值
self.values[state] = max(state_values)
if __name__ == "__main__":
# 1. 创建测试环境
test_env = gym.make(ENV_NAME)
# 2. 创建智能体
agent = Agent()
# 3. 创建TensorBoard记录器
writer = SummaryWriter(comment="-v-iteration")
# 4. 训练循环
iter_no = 0
best_reward = 0.0
while True:# 无限循环，直到达到目标
iter_no += 1
# 步骤A: 收集随机经验
agent.play_n_random_steps(100)
# 步骤B: 价值迭代
agent.value_iteration()
# 步骤C: 评估当前策略
reward = 0.0
for _ in range(TEST_EPISODES):
reward += agent.play_episode(test_env)# 执行一个完整片段
reward /= TEST_EPISODES # 计算平均奖励
# 步骤D: 记录和监控
writer.add_scalar("reward", reward, iter_no)
# 步骤E: 更新最佳奖励
if reward > best_reward:
print("Best reward updated %.3f -> %.3f" % (
best_reward, reward))
best_reward = reward
if reward > 0.80:
print("Solved in %d iterations!" % iter_no)
break
writer.close()价值迭代中的动作转移概率和期望计算的完整流程：
1）收集数据 ：play_n_random_steps 收集 (s,a,s',r) 数据
2）估计概率 ：transits 表记录转移次数 → 估计转移概率
3）计算期望 ：calc_action_value 用概率加权计算期望回报
4）价值更新 ：value_iteration 更新状态价值为最大期望回报
b、tensorboard查看
打开python目录，运行cmd窗口，执行命令行：
python.exe -m tensorboard.main --logdir=D:\PythonProject\DeepReinforcementLearningHands-On\Chapter05\runs
查看结果：
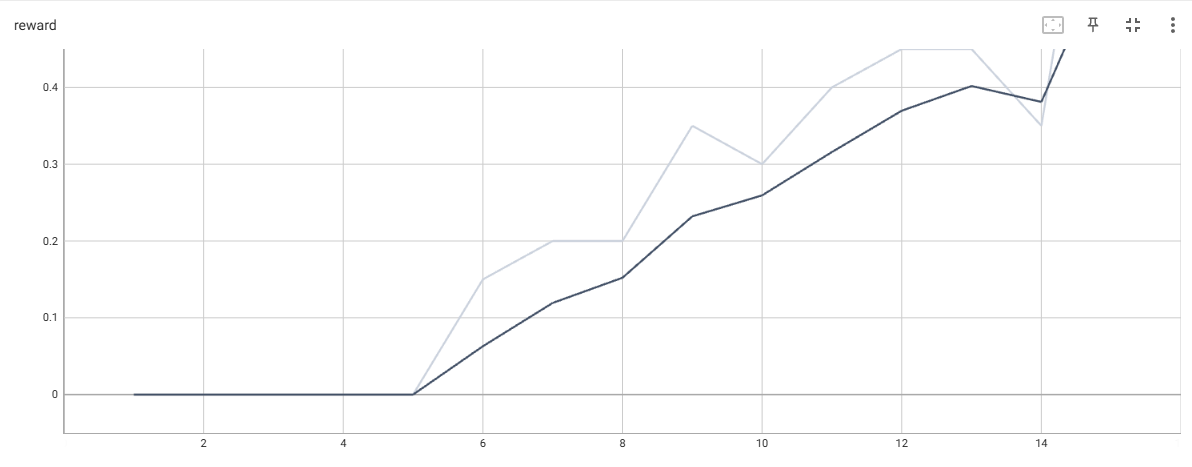
FrozenLake-4*4的奖励动态
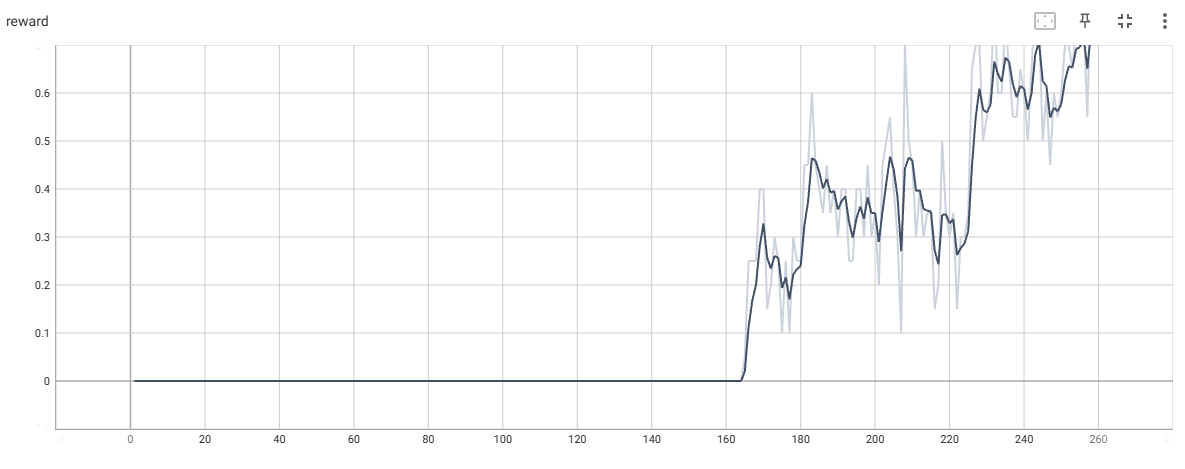
FrozenLake-8*8的奖励动态
在上图中，FrozenLake-8*8需要150~1000次迭代才能收敛，大多数情况下，需要等待第一个成功片段后才会很快收敛。
（2）q_iteration
a、代码实现
python
#!/usr/bin/env python3
import gym
import collections
from tensorboardX import SummaryWriter
ENV_NAME = "FrozenLake-v0"
#ENV_NAME = "FrozenLake8x8-v0" # uncomment for larger version
GAMMA = 0.9
TEST_EPISODES = 20
class Agent:
"""
基于模型的强化学习代理，使用动态规划（价值迭代）方法，但直接更新状态-动作值函数Q(s,a)。
学习方法如下：
1. 收集环境动态的随机经验（蒙特卡洛采样）
2. 构建环境的转移模型（转移表和奖励表）
3. 使用类似价值迭代的算法直接更新状态-动作值函数Q(s,a)
4. 根据Q(s,a)函数选择最优动作
与标准价值迭代的区别：
- 标准方法：更新状态值V(s)，然后通过贝尔曼方程计算Q(s,a)
- 本方法：直接更新状态-动作值Q(s,a)，跳过中间的状态值V(s)
属性：
env: Gym环境实例
state: 当前环境状态
rewards: 奖励表，记录(state, action, next_state)的即时奖励
transits: 转移表，记录(state, action)转移到各next_state的次数
values: 状态-动作值表，记录每个状态-动作对的价值估计Q(s,a)
"""
def __init__(self):
"""
初始化代理。
创建Gym环境实例，并初始化经验表和状态-动作值表。
注意：
这里的values表存储的是Q(s,a)值，而不是V(s)值。
键为(state, action)元组，值为该状态-动作对的期望回报。
"""
self.env = gym.make(ENV_NAME)# 创建Gym环境
self.state = self.env.reset()# 获取第一个观察结果
self.rewards = collections.defaultdict(float)# 奖励表：R(s,a,s')
self.transits = collections.defaultdict(collections.Counter)# 转移表：P(s'|s,a)的计数
self.values = collections.defaultdict(float)# 状态-动作值表：Q(s,a)
def play_n_random_steps(self, count):
"""
执行随机步骤以收集环境动态信息（蒙特卡洛探索）。
通过随机动作收集状态转移和奖励信息，用于构建环境模型。
输入：count: 要执行的随机步骤数量
流程：
1. 随机选择动作
2. 执行动作，观察新状态和奖励
3. 记录奖励和状态转移
4. 如果情节结束则重置环境
"""
for _ in range(count):
action = self.env.action_space.sample() # 随机选择一个动作
new_state, reward, is_done, _ = self.env.step(action) # 执行动作
# 记录奖励：状态-动作-新状态 对应的奖励
self.rewards[(self.state, action, new_state)] = reward
# 记录状态转移：状态-动作 从(state, action)转移到new_state的次数
self.transits[(self.state, action)][new_state] += 1
# 更新当前状态（如果情节结束则重置环境）
self.state = self.env.reset() if is_done else new_state
def select_action(self, state):
"""
使用贪心策略选择当前状态下的最优动作。
直接从Q(s,a)表中查找最大值，无需实时计算。
输入： state: 当前状态
输出： best_action: 最优动作
流程：
1. 初始化 best_action = None, best_value = None
2. 对于每个可能的动作 action：
a. 从Q表中获取动作价值 values[(state, action)]
b. 如果这是第一个动作，或价值更高：
更新 best_value = action_value
更新 best_action = action
3. 返回 best_action
"""
best_action, best_value = None, None
# 遍历所有可能的动作
for action in range(self.env.action_space.n):
# 直接从Q表中获取状态-动作值
action_value = self.values[(state, action)]
# 选择值最大的动作
if best_value is None or best_value < action_value:
best_value = action_value
best_action = action
return best_action
def play_episode(self, env):
"""
使用当前策略执行一个完整的情节，并更新环境模型。
基于当前的Q(s,a)函数选择动作，同时收集新的经验数据。
输入： env: 环境实例
输出： total_reward: 该情节获得的总奖励
流程：
1. 初始化 total_reward = 0
2. 重置环境，获取初始状态 state
3. While True:
a. 根据Q(s,a)表选择最优动作 action = select_action(state)
b. 执行动作，得到新状态、奖励、完成标志
c. 记录奖励：rewards[(state, action, new_state)] = reward
d. 记录转移：transits[(state, action)][new_state] += 1
e. 累加奖励：total_reward += reward
f. 如果完成：break
g. 否则：更新状态 state = new_state
4. 返回 total_reward
"""
total_reward = 0.0
state = env.reset()
while True:
# 使用贪心策略选择动作
action = self.select_action(state)
# 执行动作
new_state, reward, is_done, _ = env.step(action)
# 更新经验存储
self.rewards[(state, action, new_state)] = reward
self.transits[(state, action)][new_state] += 1
# 累加奖励
total_reward += reward
# 如果回合结束则退出循环
if is_done:
break
# 更新状态
state = new_state
return total_reward
def value_iteration(self):
"""
执行类价值迭代算法，直接更新状态-动作值函数Q(s,a)。
算法原理：
直接应用贝尔曼最优方程更新Q(s,a):
Q(s,a) = Σ_{s'} P(s'|s,a)[R(s,a,s') + γ * max_{a'} Q(s',a')]
与标准价值迭代的区别：
标准算法：V(s) = max_a Σ P(s'|s,a)[R(s,a,s') + γV(s')]
本算法：直接计算并存储Q(s,a)，省略了V(s)中间表示
流程：
1. 遍历环境中所有状态
2. 对于每个状态，遍历所有可能的动作
3. 对每个动作，计算其期望回报：
a. 获取从(state, action)出发的所有可能转移
b. 对每个转移，计算：即时奖励 + 折扣因子 * 下一状态的最优Q值
c. 用转移概率加权求和
4. 将计算结果直接存储为Q(s,a)
"""
# 遍历所有状态
for state in range(self.env.observation_space.n):
# 遍历所有可能的动作
for action in range(self.env.action_space.n):
action_value = 0.0 # 初始化动作价值
# 获取从(state, action)出发的状态转移统计
target_counts = self.transits[(state, action)]
total = sum(target_counts.values()) # 计算总转移次数
# 计算动作的期望值（考虑所有可能的下一个状态）
for tgt_state, count in target_counts.items():
# 构建奖励键，获取即时奖励
key = (state, action, tgt_state)
reward = self.rewards[key]
# 选择下一个状态的最优动作
best_action = self.select_action(tgt_state)
# 计算贝尔曼方程的值：奖励 + 折扣因子 * 下一状态的最优Q值
# 注意：这里使用Q(tgt_state, best_action)而不是V(tgt_state)
val = reward + GAMMA * \
self.values[(tgt_state, best_action)]
# 加权平均（基于转移频率）
# 转移概率 = count / total
action_value += (count / total) * val
self.values[(state, action)] = action_value
if __name__ == "__main__":
"""
强化学习代理的主训练循环。
训练流程：
1. 初始化环境、代理和TensorBoard记录器
2. 循环执行以下步骤直到任务解决（奖励达到阈值）：
a. 随机探索收集经验
b. 执行值迭代算法更新值函数
c. 测试当前策略性能
d. 记录和评估训练进展
退出条件：
- 平均测试奖励达到0.80（任务解决）
"""
test_env = gym.make(ENV_NAME)
agent = Agent()
writer = SummaryWriter(comment="-q-iteration")
iter_no = 0
best_reward = 0.0
while True:
iter_no += 1
# 阶段1: 随机探索收集经验
# 执行100个随机步骤，更新环境模型（转移表和奖励表）
agent.play_n_random_steps(100)
# 阶段2: 策略改进
# 使用收集的经验执行值迭代算法，更新值函数
agent.value_iteration()
# 阶段3: 策略评估
# 评估当前策略的性能
reward = 0.0
for _ in range(TEST_EPISODES):
# 使用当前策略在测试环境中执行一个完整回合
reward += agent.play_episode(test_env)
reward /= TEST_EPISODES# 计算平均奖励（策略性能指标）
writer.add_scalar("reward", reward, iter_no)
# 检查是否已解决任务（奖励达到阈值）
# 注：0.80是特定于FrozenLake-v0环境的成功阈值
if reward > best_reward:
print("Best reward updated %.3f -> %.3f" % (best_reward, reward))
best_reward = reward
if reward > 0.80:
print("Solved in %d iterations!" % iter_no)
break
writer.close()b、tensornoard查看
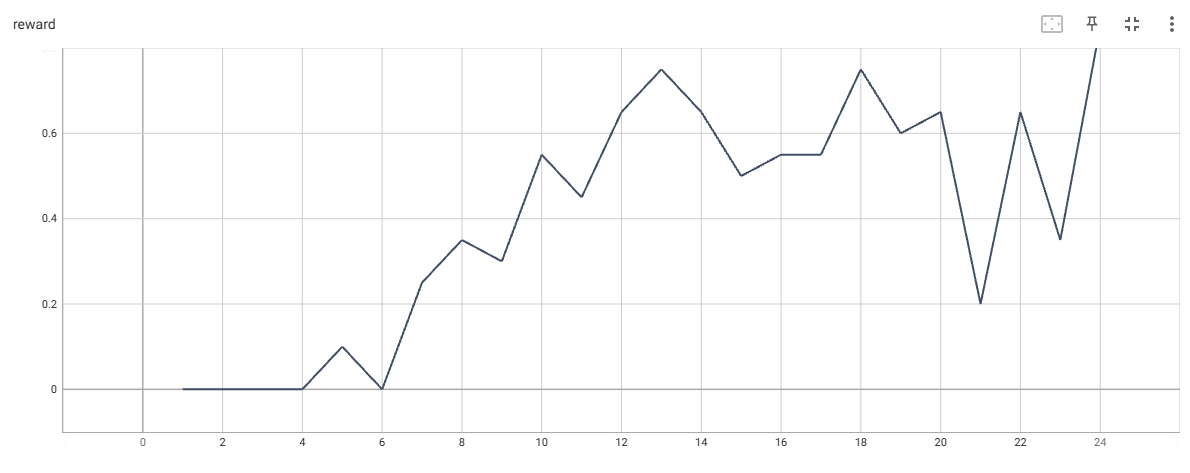
FrozenLake-4*4的奖励动态
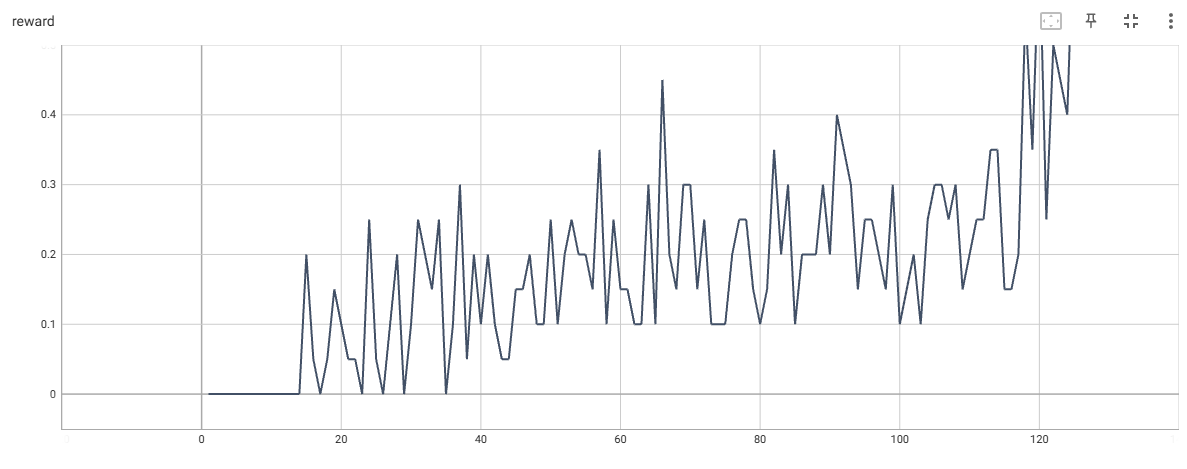
FrozenLake-8*8的奖励动态
六、价值迭代法与交叉熵对比
相对于交叉熵方法，价值迭代基于状态的价值迭代方法在80%情况下，可以在1s内找到一个较好的策略来解决该环境的问题，交叉熵方法需要几小时才能达到60%成功率。价值迭代法收敛较快的原因如下：
- 价值迭代的样本效率更高。交叉熵使用动作在片段上的随机结果(例如，平均6~8步随机动作），使得交叉熵方法很难理解片段中的什么动作是正确、什么动作是错误；价值迭代中，通过估计动作转移概率，并计算期望值给出动作的概率性结果，比随机迭代更快。
- 价值迭代不需要完整的片段（完整一局）即可开始学习。在极端的情况下，仅需要一个例子就可以开始更新价值。在Frozenlake中，由于奖励的结构（仅在成功达到目标状态后才得到奖励1），仍然需要至少成功完成一个片段才能从有用的价值表中进行学习，在更复杂的环境中可能会是一个挑战。