2025-12-11 hetao1733837的刷题笔记
LG5787 【模板】线段树分治 / 二分图
原题链接:【模板】线段树分治 / 二分图
分析
我好像有点理解了......
13点39分
卧槽,豁然开朗!这玩意就是说利用线段树,把一段区间扔进整棵树,然后线段树每个点用 v e c t o r vector vector 记录这段时间消失的节点,在分治的时候,取出对应时间段的线段树,然后判断是不是二分图就行了(并查集)。
行,继续理解撤销。
那似乎很容易想了。哎,我的二分图并不熟练。
正解
cpp
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 200005;
int n, m, k;
int fa[N << 1], sz[N << 1];
struct node{
int p, v;
node(int pos, int val){
p = pos;
v = val;
}
};
stack<node> father, size;
vector<int> tr[N << 2];
vector<bool> res;
int find(int x){
return x == fa[x] ? x : find(fa[x]);
}
void merge(int x, int y){
int fx = find(x), fy = find(y);
if (fx == fy)
return ;
if (sz[fx] < sz[fy])
swap(fx, fy);
size.push(node(fy, sz[fy]));
sz[fx] += sz[fy];
father.push(node{fy, fa[fy]});
fa[fy] = fx;
}
void work(){
fa[father.top().p] = father.top().v;
father.pop();
sz[size.top().p] = size.top().v;
size.pop();
}
void modify(int p, int l, int r, int s, int t, int val){
if (s <= l && r <= t){
tr[p].push_back(val);
return ;
}
int mid = (l + r) >> 1;
if (s <= mid)
modify(p << 1, l, mid, s, t, val);
if (t > mid)
modify(p << 1 | 1, mid + 1, r, s, t, val);
}
struct edge{
int u, v;
}e[N];
void solve(int p, int l, int r){
auto lvl = father.size();
bool flag = 1;
for (auto tmp : tr[p]){
int fu = find(e[tmp].u), fv = find(e[tmp].v);
if (fu == fv){
for (int i = l; i <= r; i++)
res.push_back(false);
flag = false;
break;
}
merge(e[tmp].u, e[tmp].v + n);
merge(e[tmp].v, e[tmp].u + n);
}
if (flag){
if (l == r){
res.push_back(true);
}
else{
int mid = (l + r) >> 1;
solve(p << 1, l, mid);
solve(p << 1 | 1, mid + 1, r);
}
}
while (father.size() > lvl){
work();
}
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m >> k;
for (int i = 1; i <= (n << 1); i++){
fa[i] = i;
sz[i] = 1;
}
for (int i = 1; i <= m; i++){
int x, y, l, r;
cin >> e[i].u >> e[i].v >> l >> r;
modify(1, 1, k, l + 1, r, i);
}
solve(1, 1, k);
for (auto v : res){
if (v)
cout << "Yes" << '\n';
else
cout << "No" << '\n';
}
}LG4219 [BJOI2014] 大融合
原题链接:[BJOI2014] 大融合
分析
首先应该明确的是,如何求取树上经过某一条边的路径数量,比较显然的就是,呃,还是有个图好一点,我找一个。
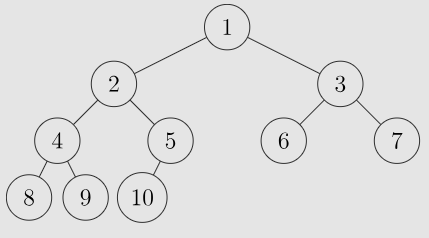
好的,对于节点 1 1 1 和节点 2 2 2 之间那一条边,其左部有 2 , 4 , 5 , 8 , 9 , 10 2,4,5,8,9,10 2,4,5,8,9,10 共 6 6 6 个点,其右部有 1 , 3 , 6 , 7 1,3,6,7 1,3,6,7 共 4 4 4 个点,则经过该边的路径数量共 6 × 4 = 24 6\times 4=24 6×4=24 条。
从这个角度出发,我要多维护每个连通块内部每个点的子树大小。
同样对于时间去处理?
那我会有种离线思路。
我直接建出最终的树,然后对于一条边的加入,令其在初始时间到加入时间这段时间不可用,就变成了模板,但我好像不太会动态维护子树大小,细想起来其实也不难吧......
好像给的思路差不多,行,我搓一下代码。
比模板多的恐怕也只有各种map了,其实可以统一存进一个 s t r u c t struct struct 里,显得优雅一些?
正解
cpp
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 100005;
char op;
int n, q, fa[N], sz[N];
struct node{
int pos, val;
node(int p, int v){
pos = p;
val = v;
}
};
stack<node> siz, father;
int find(int x){
return x == fa[x] ? x : find(fa[x]);
}
void merge(int x, int y){
x = find(x);
y = find(y);
if (x == y)
return ;
if (sz[x] < sz[y])
swap(x, y);
siz.push(node(x, sz[x]));
sz[x] += sz[y];
father.push(node(y, fa[y]));
fa[y] = x;
}
void work(){
fa[father.top().pos] = father.top().val;
father.pop();
sz[siz.top().pos] = siz.top().val;
siz.pop();
}
vector<pair<int, int>> tr[N << 4];
void modify(int p, int l, int r, int s, int t, pair<int, int> v){
if (s <= l && r <= t){
tr[p].push_back(v);
return ;
}
int mid = (l + r) >> 1;
if (s <= mid)
modify(p << 1, l, mid, s, t, v);
if (t > mid)
modify(p << 1 | 1, mid + 1, r, s, t, v);
}
int tim;
map<pair<int, int>, int> tims;
struct opt{
int l, r;
pair<int, int> v;
}opp[N << 3];
int ncnt;
map<int, int> ask;
map<int, pair<int, int>> asklr;
int ans[N << 3];
void solve(int p, int l, int r){
int lvl = father.size();
for (auto u : tr[p]){
merge(u.first, u.second);
}
if (l == r){
if (ask[l]){
int x = asklr[l].first, y = asklr[l].second;
ans[l] = sz[find(x)] * sz[find(y)];
}
}
else{
int mid = (l + r) >> 1;
solve(p << 1, l, mid);
solve(p << 1 | 1, mid + 1, r);
}
while (father.size() > lvl){
work();
}
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> q;
for (int i = 1; i <= n; i++){
fa[i] = i;
sz[i] = 1;
}
for (int cs = 1; cs <= q; cs++){
cin >> op;
int x, y;
cin >> x >> y;
if (op == 'A'){
tims[{x, y}] = ++tim;
}
else{
pair<int, int> tmp = {x, y};
opp[++ncnt] = {tims[tmp], ++tim, tmp};
ask[++tim] = 1;
asklr[tim] = tmp;
tims[tmp] = ++tim;
}
}
int tmp = ++tim;
for (auto i : tims){
opp[++ncnt] = {tims[i.first], tmp, i.first};
}
for (int i = 1; i <= ncnt; i++){
modify(1, 1, tim, opp[i].l, opp[i].r, opp[i].v);
}
solve(1, 1, tim);
for (int i = 1; i <= tim; i++){
if (ask[i]){
cout << ans[i] << '\n';
}
}
}LG2056 [ZJOI2007] 捉迷藏
原题链接:[ZJOI2007] 捉迷藏
分析
这不是我昨天被 h a c k hack hack 的点分树题吗?今天又碰到了,这是让我和他死磕到底吗?大课间之前最好能吃出来!
坏了,代码里有 b i t s e t bitset bitset,我还没学!
那咋办?现学!
并不很难吧,难道我可以做 LG11831 [省选联考 2025] 追忆 了?假的,黑题要是随便做,场上碰见的都成不可做题了。
从点分治的角度去想,距离最长的点显然最好分别在两棵子树内。
改变颜色似乎是在一段时间不可选(亮了),一段时间可选(不亮),那就成了板子?
真假的?找题解求证一下。
错误总结
错误点在于两点最长距离的计算方式,正确的方式是找到树上黑点作为端点构成的直径,然后对于每次新加入黑点点集后的直径,只可能维持不变、一个端点不变另一个端点变成新加入的黑点。
感觉被骗了,ber,阴成啥了?这个所谓直径的说法不过是我说法的形式化?感觉我理解地还算对。
但是,树上最长链问题就要往直径上想! ,详情参考 L G 8173 [ C E O I 2021 ] N e w s p a p e r s LG8173 [CEOI 2021] Newspapers LG8173[CEOI2021]Newspapers。
正解
cpp
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 500005, M = 500005;
int n, q;
char op;
struct node{
int pos, val;
node (int p, int v){
pos = p;
val = v;
}
};
vector<int> e[N];
int sz[N], de[N], fa[N], top[N], son[N];
//树剖求 LCA
void dfs1(int u, int pa){
de[u] = de[pa] + 1;
fa[u] = pa;
sz[u] = 1;
for (auto v : e[u]){
if (v == pa)
continue;
dfs1(v, u);
sz[u] += sz[v];
if (sz[v] > sz[son[u]])
son[u] = v;
}
}
void dfs2(int u, int tp){
top[u] = tp;
if (son[u]){
dfs2(son[u], tp);
}
for (auto v : e[u]){
if (v == fa[u] || v == son[u])
continue;
dfs2(v, v);
}
}
int LCA(int x, int y){
while (top[x] != top[y]){
if (de[top[x]] < de[top[y]])
swap(x, y);
x = fa[top[x]];
}
if (de[x] < de[y])
return x;
return y;
}
int dist(int x, int y){
return de[x] + de[y] - de[LCA(x, y)] * 2;
}
vector<int> tr[N << 2];
void modify(int p, int l, int r, int s, int t, int val){
if (s <= l && r <= t){
tr[p].push_back(val);
return ;
}
int mid = (l + r) >> 1;
if (s <= mid)
modify(p << 1, l, mid, s, t, val);
if (t > mid)
modify(p << 1 | 1, mid + 1, r, s, t, val);
}
stack<pair<int, int>> stk;
int u, v, ans[N];
void solve(int p, int l, int r){
auto lvl = stk.size();
for (auto x : tr[p]){
stk.push({u, v});
if (!u && !v){
u = x;
v = x;
}
else{
vector<int> vct = {dist(u, v), dist(u, x), dist(x, v)};
sort(vct.begin(), vct.end(), greater<int>());
if (vct[0] == dist(u, x))
v = x;
else if (vct[0] == dist(x, v))
u = x;
}
}
if (l == r){
if (!u || !v)
ans[l] = -1;
else
ans[l] = dist(u, v);
}
else{
int mid = (l + r) >> 1;
solve(p << 1, l, mid);
solve(p << 1 | 1, mid + 1, r);
}
while (stk.size() != lvl){
auto top = stk.top();
u = top.first;
v = top.second;
stk.pop();
}
}
int lst[N];
bitset<N> col;
bitset<M> ha;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
for (int i = 1; i < n; i++){
int u, v;
cin >> u >> v;
e[u].push_back(v);
e[v].push_back(u);
}
dfs1(1, 0);
dfs2(1, 1);
for (int i = 1; i <= n; i++){
lst[i] = 1;
}
cin >> q;
for (int i = 2; i <= q + 1; i++){
cin >> op;
if (op == 'C'){
int x;
cin >> x;
if (!col[x]){
col[x] = 1;
modify(1, 1, q + 2, lst[x], i, x);
}
else{
col[x] = 0;
lst[x] = i;
}
}
else{
ha[i] = 1;
}
}
for (int i = 1; i <= n; i++){
if (!col[i]){
modify(1, 1, q + 2, lst[i], q + 2, i);
}
}
solve(1, 1, q + 2);
for (int i = 1; i <= q + 2; i++){
if (ha[i])
cout << ans[i] << '\n';
}
}LG4556 【模板】线段树合并 / [Vani有约会] 雨天的尾巴
原题链接:【模板】线段树合并 / [Vani有约会] 雨天的尾巴
分析
啊?难道开值域棵线段树?有点恐怖了!
假的,线段树合并即可。思想我显然理解了,但是吧,pyd上课不变代码写全是何意味?发现还得套 LCA?
正解
cpp
#include <bits/stdc++.h>
using namespace std;
const int N = 100005;
const int V = 100001;
int n, m, f[N][22], de[N], ans[N];
vector<int> e[N];
struct node{
int id, cnt;
friend bool operator<(node tmp1, node tmp2){
if (tmp1.cnt == tmp2.cnt){
return tmp1.id > tmp2.id;
}
return tmp1.cnt < tmp2.cnt;
}
friend node operator+(node tmp1, node tmp2){
return (node){tmp1.id, tmp1.cnt + tmp2.cnt};
}
};
vector<node> tag[N];
struct segtree{
node tr[N * 40];
int ls[N * 40], rs[N * 40];
int ncnt;
void init(){
ncnt = n;
for(int i = 1; i <= n; i++){
tr[i] = {0, 0};
ls[i] = rs[i] = 0;
}
}
void pushup(int p){
tr[p] = max(tr[ls[p]], tr[rs[p]]);
}
void modify(int p, int l, int r, node val){
if (r - l == 1){
tr[p] = val + tr[p];
return ;
}
int mid = (l + r) >> 1;
if (val.id < mid){
if (!ls[p]){
ls[p] = ++ncnt;
tr[ls[p]] = {0, 0};
}
modify(ls[p], l, mid, val);
}
else{
if (!rs[p]){
rs[p] = ++ncnt;
tr[rs[p]] = {0, 0};
}
modify(rs[p], mid, r, val);
}
pushup(p);
}
void merge(int x, int y, int l, int r){
if (!x || !y) return;
if (r - l == 1){
tr[x] = tr[x] + tr[y];
return ;
}
int mid = (l + r) >> 1;
if (ls[x] && ls[y]){
merge(ls[x], ls[y], l, mid);
}
else if (ls[y]){
ls[x] = ls[y];
}
if (rs[x] && rs[y]){
merge(rs[x], rs[y], mid, r);
}
else if (rs[y]){
rs[x] = rs[y];
}
pushup(x);
}
}T;
void init(){
for (int i = 1; i <= 20; i++)
for (int u = 1; u <= n; u++)
f[u][i] = f[f[u][i - 1]][i - 1];
}
void dfs(int u){
for (auto v : e[u]){
if (v != f[u][0]){
f[v][0] = u;
de[v] = de[u] + 1;
dfs(v);
}
}
}
int lca(int x, int y){
if (de[x] < de[y]){
swap(x, y);
}
int k = de[x] - de[y];
for (int i = 0; i <= 20; i++){
if (k & (1 << i))
x = f[x][i];
}
if (x == y)
return y;
for (int i = 20; i >= 0; i--)
if (f[x][i] != f[y][i]){
x = f[x][i];
y = f[y][i];
}
return f[x][0];
}
void Merge(int u){
for (auto v : e[u]){
if (v != f[u][0]){
Merge(v);
T.merge(u, v, 0, V);
}
}
for (auto k : tag[u]){
T.modify(u, 0, V, k);
}
ans[u] = T.tr[u].id;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
T.init();
for (int i = 1; i < n; i++){
int a, b;
cin >> a >> b;
e[a].push_back(b);
e[b].push_back(a);
}
dfs(1);
init();
for (int i = 1; i <= m; i++){
int x, y, z;
cin >> x >> y >> z;
int LCA = lca(x, y);
tag[x].push_back((node){z, 1});
tag[y].push_back((node){z, 1});
tag[LCA].push_back((node){z, -1});
if(f[LCA][0] > 0)
tag[f[LCA][0]].push_back((node){z, -1});
}
Merge(1);
for (int i = 1; i <= n; i++){
cout << ans[i] << '\n';
}
return 0;
}何意味?凭啥?我左移 5 位开 32 倍凭啥卡我?开40倍你过了?
LG6773 [NOI2020] 命运
原题链接:[NOI2020] 命运
分析
19点28分
不行,我先写到蓝,这样洛谷上蓝题数量就和黄题一样了,嘻嘻。
20点37分
哦,终于把下面那道题过了。
回家打 CF!这题太......难以评价......
正解
cpp
LG2279 [HNOI2003] 消防局的设立
原题链接:[HNOI2003] 消防局的设立
分析
自己打了一发,过了小样例,交上去 10pts,哭晕在厕所/(ㄒoㄒ)/~~
显然我是从 ZR 题单的树形 D P DP DP 里把这题扒出来的,所以直接树形 D P DP DP ,设 f u , 0 / 1 / 2 f_{u,0/1/2} fu,0/1/2 表示 u u u 节点,其子树内最近的消防站距离他 0 / 1 / 2 0/1/2 0/1/2 的建造消防站个数。
错误分析
我们只考虑了 u u u 的子树,但是, u u u 为什么不能从其祖先转移而来?
那么,多设两种状态,即设 f u , 0 / 1 / 2 / 3 / 4 f_{u,0/1/2/3/4} fu,0/1/2/3/4 表示从节点 u u u 向上覆盖 2 / 1 / 0 / − 1 / − 2 2/1/0/-1/-2 2/1/0/−1/−2 层的最小消防站个数。
转移显然,
f u , 0 = 1 + ∑ v ∈ s o n [ u ] f v , 4 f_{u, 0}=1+\sum\limits_{v\in son[u]}f_{v, 4} fu,0=1+v∈son[u]∑fv,4
f u , 1 = min v ∈ s o n [ u ] ( f v , 0 + ∑ t ∈ s o n [ u ] , t ≠ v f t , 3 , f u , 0 ) f_{u, 1}=\min\limits_{v\in son[u]}(f_{v,0}+\sum\limits_{t\in son[u],t\neq v}f_{t,3}, f_{u,0}) fu,1=v∈son[u]min(fv,0+t∈son[u],t=v∑ft,3,fu,0)
f u , 2 = min v ∈ s o n [ u ] ( f v , 1 + ∑ t ∈ s o n [ u ] , t ≠ v f t , 2 , f u , 0 , f u , 1 ) f_{u, 2}=\min\limits_{v\in son[u]}(f_{v,1}+\sum\limits_{t\in son[u],t\neq v}f_{t,2}, f_{u,0},f_{u,1}) fu,2=v∈son[u]min(fv,1+t∈son[u],t=v∑ft,2,fu,0,fu,1)
f u , 3 = min ( ∑ v ∈ s o n [ u ] f v , 2 , f u , 0 , f u , 1 , f u , 2 ) f_{u,3}=\min(\sum\limits_{v\in son[u]}f_{v,2},f_{u, 0},f_{u, 1},f_{u, 2}) fu,3=min(v∈son[u]∑fv,2,fu,0,fu,1,fu,2)
f u , 4 = min ( ∑ v ∈ s o n [ u ] f v , 3 , f u , 0 , f u , 1 , f u , 2 , f u , 3 ) f_{u,4}=\min(\sum\limits_{v\in son[u]}f_{v,3},f_{u, 0},f_{u, 1},f_{u, 2},f_{u, 3}) fu,4=min(v∈son[u]∑fv,3,fu,0,fu,1,fu,2,fu,3)
正解
直接建有向,少记录一个 f a fa fa。
cpp
#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
int n;
vector<int> e[N];
int f[N][5];
void dfs(int u){
f[u][0] = 1;
f[u][3] = 0;
f[u][4] = 0;
for (auto v : e[u]){
dfs(v);
f[u][0] += f[v][4];
f[u][3] += f[v][2];
f[u][4] += f[v][3];
}
if (e[u].size() == 0){
f[u][1] = f[u][2] = 1;
}
else{
f[u][1] = f[u][2] = 0x3f3f3f3f;
for (auto v : e[u]){
int f1 = f[v][0], f2 = f[v][1];
for (auto t : e[u]){
if (v == t)
continue;
f1 += f[t][3];
f2 += f[t][2];
}
f[u][1] = min(f[u][1], f1);
f[u][2] = min(f[u][2], f2);
}
}
for (int i = 1; i <= 4; i++){
f[u][i] = min(f[u][i], f[u][i - 1]);
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
for (int i = 2; i <= n; i++){
int a;
cin >> a;
e[a].push_back(i);
}
dfs(1);
cout << f[1][2];
}