城市韧性与交通基础设施系统耦合协调度的时空演变及影响因素

该研究以山东省16个地级市2012-2021年面板数据为基础，聚焦城市韧性（UR）与交通基础设施系统（TI）的耦合协调关系，通过多模型结合的实证研究，系统分析二者的时空演变规律与影响因素，为城市可持续发展提供精准政策支撑。以下按文章结构详细拆解各部分内容，重点深化研究方法的技术细节与逻辑链条，并同步说明图片位置及核心信息：

原文：Spatiotemporal Evolution and Influencing Factors of the Coupling Coordination Degree between Urban Resilience and the Transport Infrastructure System: A Case Study of Panel Data from 16 Prefecture-Level Cities in Shandong Province, China

一、摘要（Abstract）

核心内容：明确研究背景（城市化进程中人口规模与流动性激增，给交通基础设施和韧性城市建设带来双重压力）、核心创新（将UR与TI纳入同一理论框架）、研究方法（耦合协调模型、障碍度模型）、数据范围（山东省16市10年面板数据）及四大核心结论：

UR与TI发展水平均呈动态增长态势；
二者耦合协调度持续上升（均值从0.3012升至0.4018），但整体仍处于"轻度失衡"阶段；
耦合协调度空间分布不均，济南、青岛水平显著领先；
指标层障碍因素存在城市异质性，维度层中经济韧性与交通基础设施建设水平是主要制约因素。

二、引言（Introduction）

核心内容：

现实背景：中国改革开放后城市化进入高速发展期，人口聚集导致交通需求暴涨，城市结构稳定性面临挑战，而UR（城市抵御、恢复灾害的能力）与TI（城市功能运转的核心支撑）是高质量城市化的关键要素，二者存在空间溢出效应，但全球范围内对二者系统耦合机制的研究仍显不足。
研究缺口：现有研究多单独关注UR或TI，缺乏对二者双向互动机制的量化分析；且实证研究多依赖发达城市群横截面数据，忽视区域发展异质性，难以指导差异化政策制定。
研究问题：
- UR、TI及其耦合协调度在城市化进程中的时空演变规律是什么？
- 区域内不同发展阶段城市的耦合协调障碍因素有哪些？
- 如何结合城市发展异质性制定本地化策略？
案例选择依据：山东省作为经济大省（2023年GDP增速6%）、人口大省（常住人口1.0123亿）、交通试点省（全国首个交通强国联合建设省级示范区），城市化率达65.53%，且内部包含济南、青岛等发达城市与中小欠发达城市，发展差异显著，具备典型研究价值。
研究目标：揭示UR与TI的耦合协调机制，分析其时空演变特征，识别关键影响因素，为政策制定提供科学依据。

三、文献综述（Literature Review）

核心内容：

城市韧性及其评估：
- 概念演进："韧性"源于物理学，经生态学（Holling引入）延伸至人类生态学，最终应用于城市规划、灾害应急等领域，定义为城市抵御冲击、快速恢复并保障公共安全、经济社会正常运转的能力。
- 评估体系：现有研究多从多维度构建指标体系（如京津冀地区的经济、社会、生态、设施四维指标），量化方法包括熵权法、耦合协调度模型等，但多数研究未关注指标层对整体目标的具体影响。
交通基础设施发展与规划：
- 系统构成：包含物理设施与管理人员，需从发展与应用双维度评估，其发展已从快速扩张进入高质量可持续阶段，但城市化加剧了交通拥堵，且自然灾害频发凸显其在灾后恢复中的关键作用。
- 研究热点：集中于空间溢出效应、韧性模拟、智能交通系统等，但现有研究多关注TI对UR的单向影响，缺乏系统耦合视角的分析。
二者耦合协调机制：
- 双向互动：高UR为TI提供经济（资金支持）、社会（人力保障）、生态（可持续建设导向）支撑；完善的TI促进城市资源流动、提升风险应对能力，进而增强UR。
- 研究空白：现有文献对二者耦合协调的系统性、双向性分析不足，缺乏结合具体地理空间的实证验证。

四、研究区域（Study Area）

核心内容：山东省位于中国东部沿海、黄河下游，地理坐标介于北纬34°23′-38°17′、东经114°48′-122°42′，土地面积约15.8万km²，下辖16个地级市、136个县级行政区，是国家"两横三纵"城市化战略的重要组成部分，兼具沿海与内陆城市、发达与欠发达地区特征，其UR与TI耦合发展经验对其他地区具有借鉴意义。

五、研究方法（Methodology）

核心内容：研究遵循"指标体系构建→权重计算→耦合协调度测算→时空演变分析→障碍因素识别→政策建议"的完整流程，各环节方法细节如下：

1. 指标体系与数据来源

指标体系构建：
- 城市韧性（UR）：分为经济韧性（权重0.4366）、社会韧性（0.2202）、生态韧性（0.0645）、设施韧性（0.2787）4个维度，包含21个正向指标（如人均GDP、普通高等教育招生数）和4个负向指标（如人口密度、二氧化硫排放量），覆盖经济、社会、生态、基础设施等核心维度。
- 交通基础设施（TI）：分为建设水平（0.7547）、管理水平（0.2453）2个维度，含8个正向指标（如公交运营线路长度、交通运输从业人员数），聚焦设施建设与运营管理核心环节。
- 指标选择原则：遵循科学性、全面性、代表性、可获得性。
数据来源与处理：
- 数据范围：2012-2021年面板数据，来源于《山东统计年鉴》《中国城市统计年鉴》等官方统计资料。
- 缺失值处理：采用线性插值法（通过两点间直线估算缺失值），虽可能因数据非线性趋势引入偏差，但因缺失值占比低，影响有限。

2. 核心研究方法

（1）熵权法（指标权重计算）

方法定位：客观赋权法，基于指标信息熵反映数据离散程度，离散程度越高，权重越大，结果稳定且操作简便。
计算步骤：
1. 数据标准化：消除量纲差异，正向指标采用"（原值-最小值）/（最大值-最小值）"，负向指标采用"（最大值-原值）/（最大值-最小值）"；
2. 计算指标权重（P_ij）：标准化后数据占该指标总数据的比例；
3. 计算信息熵（H_j）：H_j = -[1/ln(mk)]×Σ(P_ij×lnP_ij)，其中m=16（城市数），k=10（年份数）；
4. 计算指标权重（W_j）：W_j = (1-H_j)/Σ(1-H_j)，权重总和为1；
5. 计算综合评价值：UR综合评价值（U）=Σ(W_j×标准化指标值)，TI综合评价值（T）同理。

（2）耦合协调度模型（UR与TI耦合关系量化）

方法定位：量化两个系统的相互作用强度与协调发展水平，包含耦合度（C）、综合发展水平（S）、耦合协调度（D）三个核心指标。
核心公式：
1. 耦合度（C）：C = √[(U×T)/((U+T)/2)²]，取值范围[0,1]，值越大表示系统间相互作用越强；
2. 综合发展水平（S）：S = αU + βT，其中α=β=0.5（假设UR与TI同等重要）；
3. 耦合协调度（D）：D = √(C×S)，取值范围[0,1]，结合分类标准（Table 2）划分协调水平（如[0.3,0.4)为轻度失衡，[0.5,0.6)为勉强协调）。

（3）核密度估计法（KDE，时间演变特征分析）

方法定位：非参数估计法，无需预设数据分布，通过概率密度曲线直观展示变量的时间演变趋势，能捕捉数据聚集特征、极化趋势等。
核心公式：f(x) = (1/nh)×ΣK[(x_i - x̄)/h]，其中n为样本数，x_i为观测值，x̄为均值，h为带宽，采用高斯核函数K(x) = (1/√(2π))×exp(-x²/2)，需满足"极限为0、非负、积分值为1"等条件。
应用目的：分析2012-2021年UR与TI耦合协调度的分布位置、极化特征、分布宽度变化，揭示时间维度的演变规律。

（4）障碍度模型（影响因素识别）

方法定位：量化指标层与维度层对耦合协调度的制约程度，明确关键障碍因素，为精准施策提供依据。
核心公式：
1. 指标偏差度（M_j）：M_j = 1 - 标准化指标值（反映指标与目标值的差距）；
2. 指标障碍度（O_j）：O_j = (M_j×W_j)/Σ(M_j×W_j)×100%，取值越大，该指标对耦合协调的制约越强；
3. 维度障碍度（V_j）：V_j = Σ该维度下所有指标的O_j，反映维度层面的整体制约程度。
应用目的：分别从UR（4个维度、25个指标）和TI（2个维度、8个指标）识别影响耦合协调发展的关键因素，并对比2012-2016年（Phase 1）与2017-2021年（Phase 2）的障碍因素变化。

3. 数据可视化工具

采用ArcGIS 10.7绘制空间分布图，展示耦合协调度的空间差异；
采用核密度曲线可视化时间演变特征；
采用柱状图展示维度层与指标层障碍度。

六、结果（Results）

核心内容：

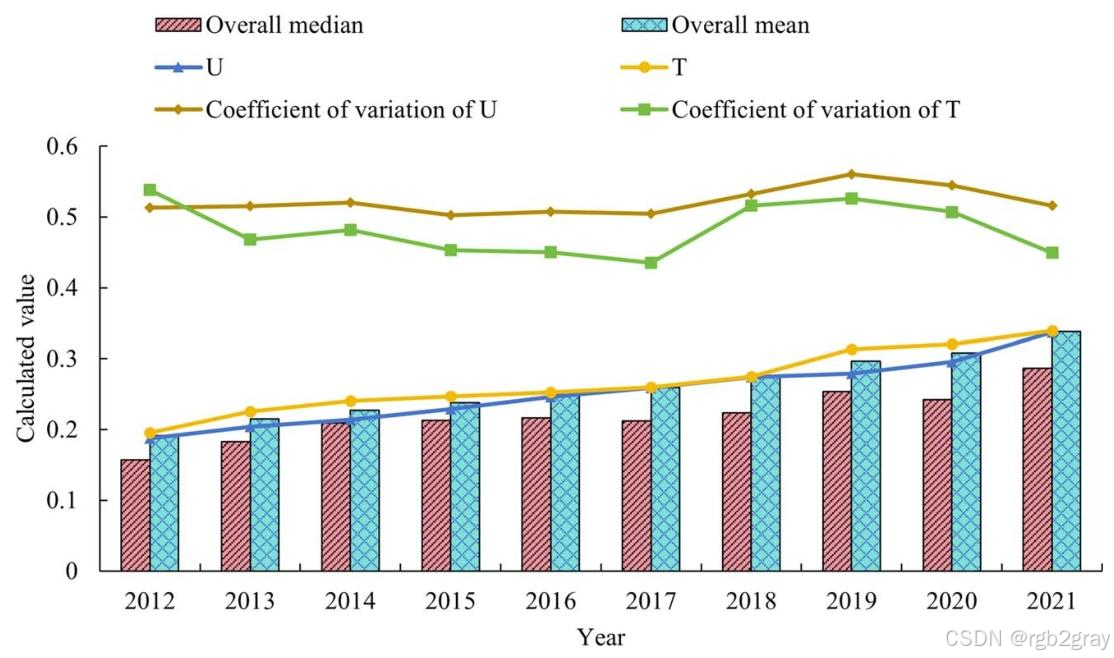
1. UR与TI发展水平分析

时间维度：2012-2021年，UR综合评价值从0.1879升至0.3370（增长79.35%），TI从0.1956升至0.3394（增长73.52%），均呈稳步上升趋势，但UR增长略快于TI，且二者变异系数（反映区域差异）呈波动下降，说明区域差距缩小但仍存在失衡。
空间维度：各地级市发展水平存在异质性，但整体均值与中位数差异较小，呈现"局部均衡、整体异质"的特征。
图片位置：该部分末尾（文中标注为Fig. 2）
图片内容：《2012-2021年UR与TI综合发展水平计算值》，以折线图展示UR（U）、TI（T）的整体均值、整体中位数，以及二者的变异系数变化，横轴为年份（2012-2021），纵轴为数值（0-0.6），直观呈现二者的时间演变与区域差异。

2. UR与TI耦合协调度分析

（1）整体特征

2012-2021年，耦合协调度均值从0.3012升至0.4018，协调水平从"轻度失衡"升级为"濒临失衡"，说明政府风险管控加强与交通基建投入增加推动了二者正向耦合，但整体协调水平仍较低（未突破0.5）。

（2）时间演变特征（KDE分析）

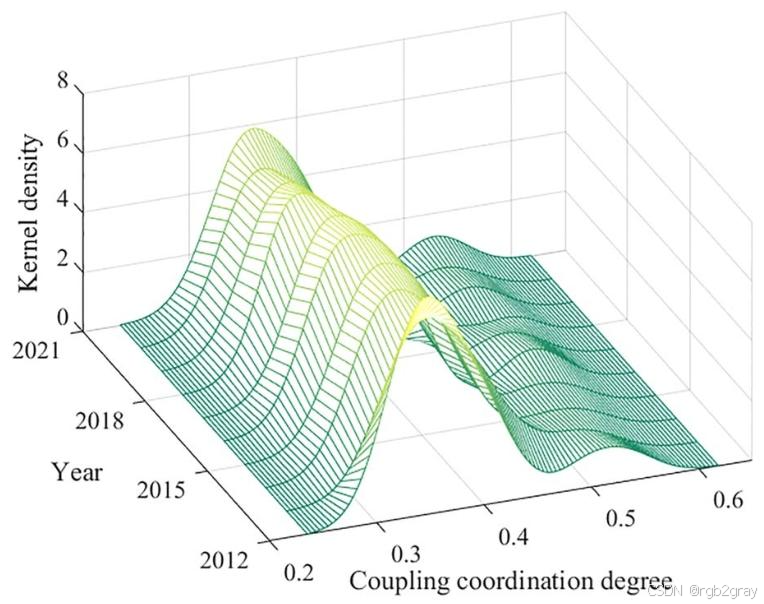
图片位置：时间演变分析部分（文中标注为Fig. 3）
图片内容：《2012-2021年UR与TI耦合协调度核密度估计曲线》，4条曲线分别对应2012、2015、2018、2021年，横轴为耦合协调度（0.2-0.6），纵轴为密度值（0-8）。
关键结论：
1. 分布位置右移：主峰从0.3附近向0.35附近移动，说明整体协调水平提升；
2. 极化特征显著：呈现双峰分布，主峰高于次峰，说明部分城市（济南、青岛）已进入高协调阶段，多数城市仍处于低失衡阶段，极化趋势明显；
3. 分布宽度稳定：曲线波高下降、宽度无显著变化，说明城市间差距持续存在，但扩大速度放缓。

（3）空间分布特征

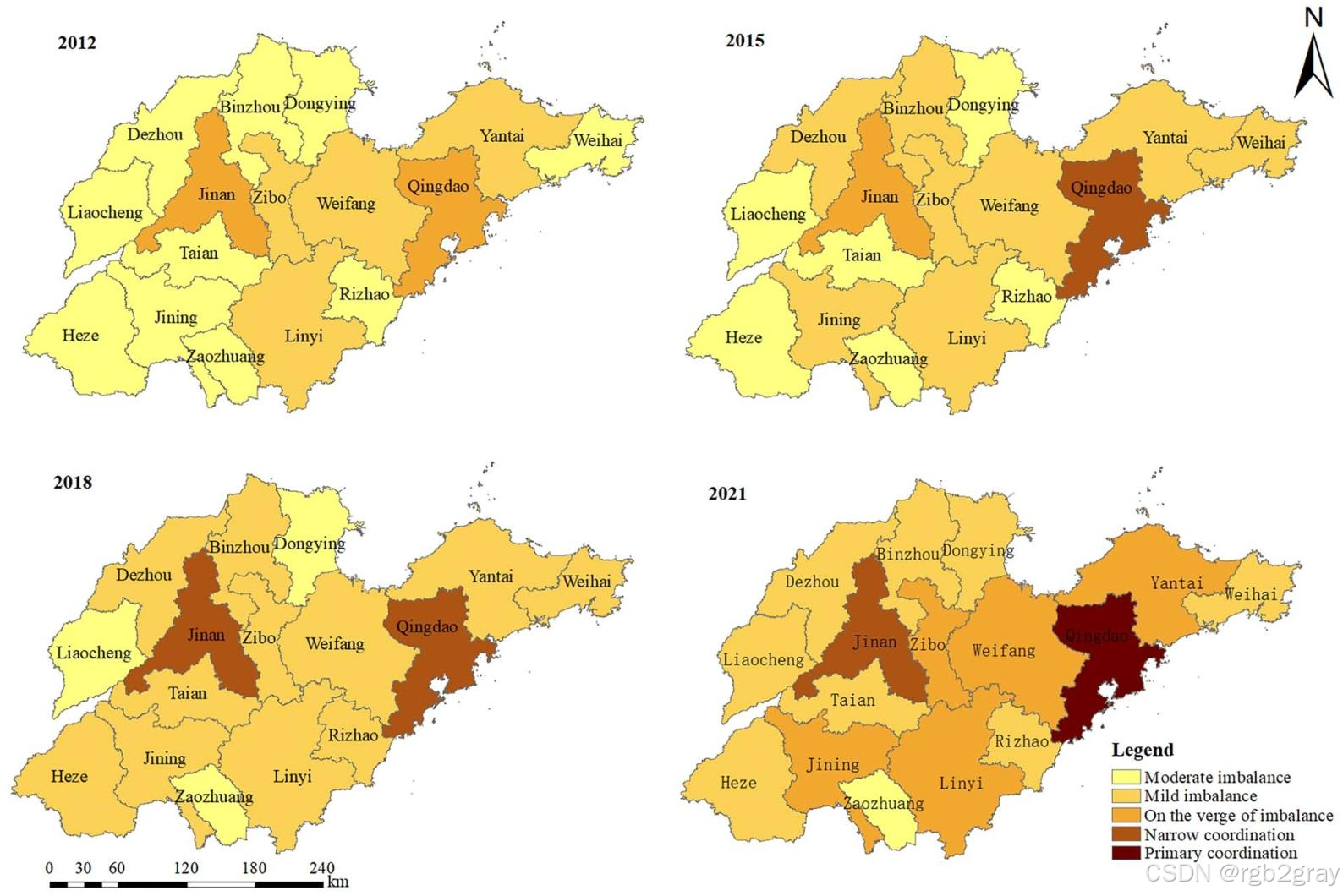
图片位置：空间分布分析部分（文中标注为Fig. 4）
图片内容：《2012、2015、2018、2021年UR与TI耦合协调度空间分布图》，4幅地图对比不同年份的空间差异，采用图例区分"中度失衡""轻度失衡""濒临失衡""勉强协调""初级协调"等级。
关键结论：
1. 空间失衡显著：东部城市（济南、青岛、烟台）协调水平高于西部城市（菏泽、聊城、枣庄）；
2. 动态变化：2012年87.5%的城市处于失衡状态，2021年降至62.5%，青岛升至"初级协调"，济南升至"勉强协调"，但枣庄仍为"中度失衡"；
3. 辐射效应：济南、青岛的高协调水平对周边城市（如淄博、潍坊）产生正向辐射，推动区域协调发展。

3. 耦合协调度影响因素分析（障碍度模型结果）

（1）指标层障碍因素

UR指标层：
- 共性障碍：实际利用外资额（A₁₆）、普通高等教育招生数（A₂₃）是多数城市的前两大障碍，反映对外开放程度不足与人力资源短缺问题；
- 城市异质：济南、青岛的次要障碍为电力消费量（A₄₅），体现发达城市能源需求与供给的矛盾；
- 阶段变化：2017-2021年，多数城市的核心障碍未缓解，部分城市新增生态类障碍（如人均公共绿地面积A₃₁）。
TI指标层：
- 共性障碍：公交运营线路长度（B₁₃）、桥梁数量（B₁₆）、交通运输从业人员数（B₂₂）是多数城市的核心障碍，合计障碍度约60%，反映公共交通覆盖不足、设施建设滞后与人力投入不足；
- 城市异质：济南的独特障碍为人均道路面积（B₁₄），青岛为道路密度（B₁₂），体现核心城市交通资源配置的特殊性；
- 阶段变化：2017-2021年，济南、青岛新增"交通财政支出占比（B₂₁）"障碍，说明核心城市交通管理投入已难以满足需求。

（2）维度层障碍因素

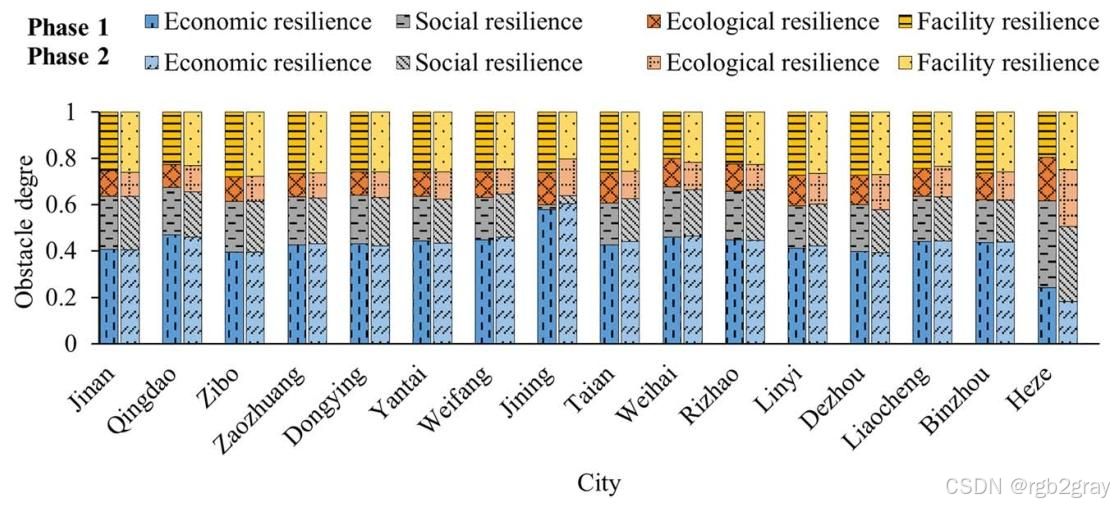
UR维度层：
- 图片位置：UR维度分析部分（文中标注为Fig. 5）
- 图片内容：《2012-2021年UR维度层障碍度》，分组柱状图展示16市在经济、社会、生态、设施韧性4个维度的障碍度（Phase 1与Phase 2）。
- 关键结论：经济韧性障碍度最高（均值42.80%），是核心制约维度；社会韧性（19.85%）、设施韧性（24.89%）次之，生态韧性最低（12.46%）；城市间差异显著（如济宁经济韧性障碍度达60%，Heze社会韧性障碍度达35%）。
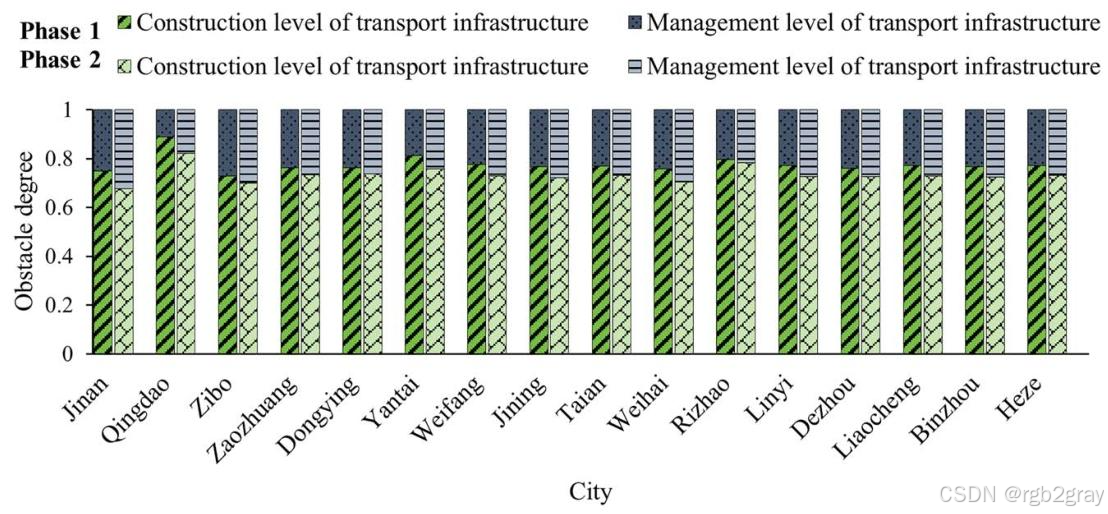
TI维度层：
- 图片位置：TI维度分析部分（文中标注为Fig. 6）
- 图片内容：《2012-2021年TI维度层障碍度》，分组柱状图展示16市在交通基建建设水平、管理水平的障碍度。
- 关键结论：建设水平障碍度均超60%，是主要制约维度；管理水平障碍度呈上升趋势，且仅济南、淄博的建设与管理障碍度差距小于40%，说明全省交通基建管理能力滞后于建设速度。

七、讨论与结论（Discussion and Conclusions）

核心内容：

核心结论：
- 耦合协调机制：UR与TI呈双向正向协同，高UR为TI提供多维度支撑，完善的TI提升UR，二者的耦合协调是高质量城市化的重要保障；
- 时空特征：二者发展水平与耦合协调度均稳步上升，但空间失衡显著，济南、青岛因经济基础、政策支持等优势处于领先地位，东部城市受核心城市辐射效应明显；
- 关键障碍：维度层中经济韧性与交通基建建设水平是共性核心障碍，指标层中对外开放、人力资源、公共交通覆盖等是主要制约因素，且障碍因素存在城市异质性。
研究创新：将UR与TI纳入同一理论框架，结合地理空间进行实证分析，量化了二者的耦合协调机制与区域异质性，弥补了现有研究的不足。
研究局限：
- 指标体系未充分考虑不同类型城市的特异性，可能影响结果普适性；
- 未建立UR与TI的因果关系，耦合协调机制分析仍偏探索性；
- TI评估指标尚未标准化，部分潜在障碍因素未纳入。
未来展望：可扩展至其他类似发展特征的地区，采用更长周期纵向数据，深入分析UR具体维度（如政策框架、社区参与）的影响，完善指标体系与研究方法。

八、政策建议（Policy Recommendations）

核心内容：

提升整体协调水平：将UR理念融入城市建设，从经济、社会、生态等多维度增强UR软硬实力；强化交通基建互联互通，推行公交优先策略，平衡发展与安全。
缩小区域空间差距：发挥济南、青岛的空间溢出效应，推动低协调度城市开展跨区域交通、产业、技术合作；灵活调整政策支持，引导社会资本参与，实现交通资源配置与经济需求匹配；优化教育与人才政策，打造人才吸引与产业发展的良性循环。
靶向破解障碍因素：
- 经济层面：欠发达城市需提升对外开放水平，核心城市需优化能源供给；
- 交通层面：优先投入地铁、轻轨等高效交通设施，加强现有道路、桥梁维护与交通枢纽升级；
- 差异化施策：沿海城市（青岛、烟台）依托区位优势发展特色产业，增强要素吸引力；西部城市聚焦基础交通设施建设与人力资源培育。

python 复制代码

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# 1. 模拟数据（基于文章指标体系，16个城市×10年面板数据）
np.random.seed(42)
cities = ["济南", "青岛", "淄博", "枣庄", "东营", "烟台", "潍坊", "济宁", 
          "泰安", "威海", "日照", "临沂", "德州", "聊城", "滨州", "菏泽"]
years = list(range(2012, 2022))
data = pd.DataFrame({
    "城市": np.repeat(cities, len(years)),
    "年份": np.tile(years, len(cities)),
    # UR核心指标（经济、社会、生态、设施韧性代表性指标）
    "人均GDP": np.random.uniform(5, 15, len(cities)*len(years)),
    "普通高等教育招生数": np.random.uniform(1, 5, len(cities)*len(years)),
    "人均公共绿地面积": np.random.uniform(10, 30, len(cities)*len(years)),
    "污水管网长度": np.random.uniform(500, 2000, len(cities)*len(years)),
    # TI核心指标（建设、管理水平代表性指标）
    "公交运营线路长度": np.random.uniform(100, 800, len(cities)*len(years)),
    "桥梁数量": np.random.uniform(50, 300, len(cities)*len(years)),
    "交通从业人员数": np.random.uniform(2, 10, len(cities)*len(years))
})

# 2. 熵权法计算指标权重
def entropy_weight(data):
    # 数据标准化（正向指标）
    data_std = (data - data.min()) / (data.max() - data.min())
    # 计算信息熵
    p = data_std / data_std.sum(axis=0)
    p = np.where(p == 0, 1e-10, p)  # 避免log(0)
    entropy = -np.sum(p * np.log(p), axis=0) / np.log(len(data))
    # 计算权重
    weight = (1 - entropy) / (1 - entropy).sum()
    return weight

# 分离UR和TI指标并计算权重
ur_cols = ["人均GDP", "普通高等教育招生数", "人均公共绿地面积", "污水管网长度"]
ti_cols = ["公交运营线路长度", "桥梁数量", "交通从业人员数"]
ur_weight = entropy_weight(data[ur_cols])
ti_weight = entropy_weight(data[ti_cols])

# 3. 计算UR和TI综合评价值
data["UR综合值"] = np.dot(data[ur_cols], ur_weight)
data["TI综合值"] = np.dot(data[ti_cols], ti_weight)

# 4. 耦合协调度模型计算
def coupling_coordination(u, t):
    # 耦合度C
    c = 2 * np.sqrt(u * t) / (u + t)
    # 综合发展水平S（α=β=0.5）
    s = 0.5 * u + 0.5 * t
    # 耦合协调度D
    d = np.sqrt(c * s)
    return c, d

data["耦合度"], data["耦合协调度"] = coupling_coordination(data["UR综合值"], data["TI综合值"])

# 5. 可视化：2012-2021年平均耦合协调度时间趋势
avg_coupling = data.groupby("年份")["耦合协调度"].mean().reset_index()
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.figure(figsize=(10, 6))
plt.plot(avg_coupling["年份"], avg_coupling["耦合协调度"], marker="o", linewidth=2, color="#2E86AB")
plt.xlabel("年份", fontsize=12)
plt.ylabel("平均耦合协调度", fontsize=12)
plt.title("山东省16市UR与TI耦合协调度时间演变（2012-2021）", fontsize=14, pad=20)
plt.grid(alpha=0.3)
plt.ylim(0.3, 0.5)  # 贴合文章结果范围（0.3012-0.4018）
plt.savefig("coupling_coordination_trend.png", dpi=300, bbox_inches="tight")
plt.show()

# 输出前5行结果验证
print("耦合协调度计算结果（前5行）：")
print(data[["城市", "年份", "UR综合值", "TI综合值", "耦合协调度"]].head())