电机功率因数深度解析：永磁同步电机的物理机制、控制策略与设计优化研究报告

摘要

在现代机电能量转换系统中，功率因数（Power Factor, PF）不仅是衡量电能利用效率的关键指标，更是决定驱动系统成本、体积及热管理设计的核心参数。随着全球工业电气化进程的加速，特别是电动汽车（EV）与精密工业自动化的普及，永磁同步电机（PMSM）凭借其高功率密度和高效率成为了主流选择。然而，PMSM的功率因数特性具有高度非线性，受到电磁设计参数与控制策略的深度耦合影响。本文旨在提供一份详尽的研究报告，从物理本源出发，系统性地阐述电机功率因数的定义与物理意义，建立PMSM在d−qd-qd−q坐标系下的功率因数数学模型，并深入探讨通过先进控制算法（如MTPA、UPF、弱磁控制）与本体电磁设计优化（如绕组拓扑、转子结构、气隙设计）来提升功率因数的路径。报告最终将视野扩展至系统级优化，分析有源前端（AFE）技术在电网侧功率因数校正中的作用及其与电机本体设计的权衡。

第一章电机功率因数的物理本质与工程意义

1.1 功率因数的基本定义与物理图像

在交流（AC）电路理论中，功率因数定义为有功功率（Active Power, PPP）与视在功率（Apparent Power, SSS）的比值，其数学表达为电压与电流基波相位差 ϕ\phiϕ 的余弦值：

PF=PS=cos⁡ϕ PF = \frac{P}{S} = \cos \phi PF=SP=cosϕ

其中，视在功率 SSS 由有功功率 PPP 和无功功率（Reactive Power, QQQ）矢量合成：

S=P2+Q2 S = \sqrt{P^2 + Q^2} S=P2+Q2

在电机驱动系统中，这三个物理量具有明确的物理对应关系：

有功功率 (PPP)：代表电机轴端输出的机械功率加上系统的电阻损耗（铜损、铁损等）。这是真正用于"做功"的能量流，直接对应于电机的转矩输出和转速。
无功功率 (QQQ)：代表在电源与电机磁场之间往复振荡的能量。在电机中，无功功率主要用于建立和维持气隙磁场（励磁）。对于感性负载（如电机），电流通常滞后于电压，消耗滞后无功。
视在功率 (SSS)：代表逆变器（Inverter）或电网必须提供的总容量。变频器、电缆和开关器件必须根据视在功率（即总电流幅值）进行额定设计，而非仅仅根据有功功率。

物理隐喻与实质：

常引用的"啤酒与泡沫"的比喻虽然直观，但在高性能电机控制中显得过于粗糙。更深层的物理实质是能量的去耦与交换。功率因数低意味着为了传输同样的有功能量，系统必须承载更大的电流分量，这些"多余"的电流分量不参与平均能量传输，却在电阻性元件上产生实实在在的热损耗（I2RI^2RI2R），并占据了逆变器的电流裕量。

1.2 异步电机与同步电机的功率因数差异

理解PMSM功率因数特性的前提，是将其与传统的感应电机（Induction Motor, IM）进行对比。

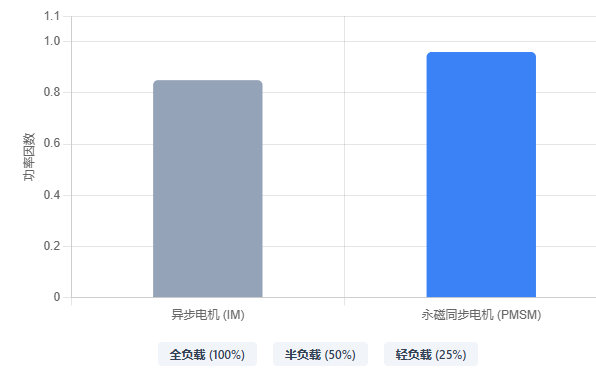
感应电机（IM） ：其转子磁场必须由定子侧的励磁电流感应产生。这意味着电网或逆变器必须始终提供滞后的无功电流分量（idi_did）来建立磁场。因此，感应电机的功率因数天然滞后且永远小于1，通常在满载时为0.8-0.9，轻载时急剧下降。
永磁同步电机（PMSM） ：其转子磁场主要由永磁体（PM）提供。理论上，如果永磁体产生的磁通足以平衡负载所需的反电势，定子就不需要提供励磁分量。这使得PMSM具有独特的功率因数可调性。通过控制定子电流矢量，PMSM可以运行在滞后、单位功率因数（PF=1），甚至超前功率因数状态。

1.3 低功率因数的系统级代价

在电动汽车和工业驱动应用中，忽视功率因数优化将带来显著的工程与经济代价：

影响维度	具体后果	物理机制
逆变器容量	成本增加、体积增大	逆变器容量由视在功率 SSS 决定。若电机 PF=0.7PF=0.7PF=0.7，为输出相同的机械功率，逆变器额定电流需增加42%。
系统效率	铜损增加、热管理压力	线路损耗与电流平方成正比 (Ploss∝I2P_{loss} \propto I^2Ploss∝I2)。低PF导致定子电流 IsI_sIs 增大，显著增加 I2RI^2RI2R 损耗。
电网侧惩罚	运营成本上升	工业用电中，低功率因数会招致电力公司的罚款，且需配置额外的无功补偿装置。
弱磁能力	高速性能受限	低PF往往伴随着较大的电感压降，这会使得电机端电压更快达到逆变器电压极限，限制高速功率输出。

第二章永磁同步电机功率因数的数学建模

为了定量分析和优化PMSM的功率因数，必须建立其在同步旋转坐标系（d−qd-qd−q 轴）下的数学模型。这种变换将三相静止坐标系下的交流量转化为随转子旋转的直流量，极大简化了控制分析。

2.1 d−qd-qd−q 轴电压方程与相量图

在 d−qd-qd−q 坐标系下，假设忽略铁损和磁路饱和的非线性影响，稳态电压方程为：

vd=Rsid−ωeLqiq v_d = R_s i_d - \omega_e L_q i_q vd=Rsid−ωeLqiq

vq=Rsiq+ωeLdid+ωeψpm v_q = R_s i_q + \omega_e L_d i_d + \omega_e \psi_{pm} vq=Rsiq+ωeLdid+ωeψpm

其中：

vd,vqv_d, v_qvd,vq：定子电压的 d,qd, qd,q 轴分量。
id,iqi_d, i_qid,iq：定子电流的 d,qd, qd,q 轴分量。
Ld,LqL_d, L_qLd,Lq：d,qd, qd,q 轴同步电感。
RsR_sRs：定子电阻。
ωe\omega_eωe：电角速度。
ψpm\psi_{pm}ψpm：永磁体磁链。

相量关系：

功率因数角 ϕ\phiϕ 是电压矢量 v\boldsymbol{v}v 与电流矢量 i\boldsymbol{i}i 之间的夹角。在高速大功率电机分析中，通常忽略定子电阻 RsR_sRs 的压降，此时电压方程简化为：

vd≈−ωeLqiq v_d \approx -\omega_e L_q i_q vd≈−ωeLqiq

vq≈ωe(Ldid+ψpm) v_q \approx \omega_e (L_d i_d + \psi_{pm}) vq≈ωe(Ldid+ψpm)

此时，反电势 E0=ωeψpmE_0 = \omega_e \psi_{pm}E0=ωeψpm 位于 qqq 轴。电枢反应产生的电压降主要体现在电感项上。

2.2 功率因数的解析表达式

功率因数 PF=cos⁡ϕPF = \cos \phiPF=cosϕ 可以通过电压矢量角 δ\deltaδ（电压超前 qqq 轴的角度）和电流矢量角 γ\gammaγ（电流超前 qqq 轴的角度，注意定义方向）导出。更直接的方法是利用 d−qd-qd−q 分量计算：

PF=PS=32(vdid+vqiq)32vd2+vq2id2+iq2 PF = \frac{P}{S} = \frac{\frac{3}{2}(v_d i_d + v_q i_q)}{\frac{3}{2} \sqrt{v_d^2 + v_q^2} \sqrt{i_d^2 + i_q^2}} PF=SP=23vd2+vq2 id2+iq2 23(vdid+vqiq)

将简化的电压方程代入，可得 PMSM 功率因数的本征表达式：

cos⁡ϕ=−ωeLqiq⋅id+ωe(Ldid+ψpm)⋅iq(ωeLqiq)2+[ωe(Ldid+ψpm)]2⋅id2+iq2 \cos \phi = \frac{-\omega_e L_q i_q \cdot i_d + \omega_e (L_d i_d + \psi_{pm}) \cdot i_q}{\sqrt{(\omega_e L_q i_q)^2 + [\omega_e (L_d i_d + \psi_{pm})]^2} \cdot \sqrt{i_d^2 + i_q^2}} cosϕ=(ωeLqiq)2+[ωe(Ldid+ψpm)]2 ⋅id2+iq2 −ωeLqiq⋅id+ωe(Ldid+ψpm)⋅iq

化简分子项（有功部分），idi_did 的项在分子中相互抵消（若 Ld=LqL_d=L_qLd=Lq），但对于凸极电机（IPM，Ld≠LqL_d \neq L_qLd=Lq），磁阻转矩项会保留。

更直观的角域表达形式为：

ϕ=arctan⁡(vdvq)−arctan⁡(idiq) \phi = \arctan\left(\frac{v_d}{v_q}\right) - \arctan\left(\frac{i_d}{i_q}\right) ϕ=arctan(vqvd)−arctan(iqid)

代入电压方程（忽略电阻）：

ϕ≈arctan⁡(−LqiqLdid+ψpm)−arctan⁡(idiq) \phi \approx \arctan\left(\frac{-L_q i_q}{L_d i_d + \psi_{pm}}\right) - \arctan\left(\frac{i_d}{i_q}\right) ϕ≈arctan(Ldid+ψpm−Lqiq)−arctan(iqid)

2.3 影响功率因数的关键变量敏感性分析

从上述解析式中，我们可以提取出决定PMSM功率因数的三个核心要素：

电感凸极率 (ξ=Lq/Ld\xi = L_q / L_dξ=Lq/Ld)：

对于内置式永磁电机（IPM），通常 Lq>LdL_q > L_dLq>Ld。较大的 qqq 轴电感会产生巨大的 ωeLqiq\omega_e L_q i_qωeLqiq 电压降，这直接导致 vdv_dvd 增大（负向）。vdv_dvd 的增大会使电压矢量 v\boldsymbol{v}v 向滞后方向大幅偏转，从而增大电压与电流的夹角，导致功率因数下降。这是高转矩密度电机（如Vernier电机）通常功率因数较低的根本原因。

特征电流与弱磁深度 (ψpm/Ld\psi_{pm} / L_dψpm/Ld)：

特征电流 Ich=ψpm/LdI_{ch} = \psi_{pm} / L_dIch=ψpm/Ld 是衡量电机抗去磁能力和弱磁范围的关键。当电机运行在深层弱磁区（高速）时，需要施加巨大的负 idi_did 来抵消 ψpm\psi_{pm}ψpm。此时，电流矢量 i\boldsymbol{i}i 几乎完全倒向负 ddd 轴（纯去磁分量），而有功电流 iqi_qiq 占比减小，导致功率因数急剧恶化。

反电势系数 (kek_eke)：

较高的反电势 E0E_0E0 在基速以下有利于提高功率因数，因为它主导了 qqq 轴电压，使得电压矢量更接近 qqq 轴（即接近有功轴）。然而，过高的反电势会导致电机过早进入弱磁区，从而在高速段牺牲功率因数。

第三章功率因数优化的控制策略

在电机本体设计确定的情况下，控制策略是调节运行点功率因数的唯一手段。不同的控制目标（最大转矩、最高效率、最小容量）对应着 id−iqi_d-i_qid−iq 平面上不同的电流轨迹，从而产生截然不同的功率因数特性。

3.1 基础控制策略：id=0i_d = 0id=0 控制

对于表贴式永磁电机（SPM），由于 Ld≈LqL_d \approx L_qLd≈Lq，没有磁阻转矩。最简单的控制策略是令 id=0i_d = 0id=0，全部电流用于产生转矩（iqi_qiq）。

PF特性 ：在 id=0i_d=0id=0 时，电压方程简化为 vd=−ωLqiqv_d = -\omega L_q i_qvd=−ωLqiq，vq=ωψpmv_q = \omega \psi_{pm}vq=ωψpm。此时功率因数角 tan⁡ϕ=vd/vq=−Lqiq/ψpm\tan \phi = v_d / v_q = -L_q i_q / \psi_{pm}tanϕ=vd/vq=−Lqiq/ψpm。
局限：随着负载电流 iqi_qiq 增加，tan⁡ϕ\tan \phitanϕ 增大，功率因数单调下降。对于电感较大的电机，满载PF可能很低。

3.2 效率最优策略：MTPA（最大转矩电流比）

对于IPM电机，为了利用磁阻转矩，必须施加负的 idi_did。MTPA控制轨迹是连接不同转矩圆与恒转矩双曲线切点的轨迹。

PF特性 ：MTPA追求的是单位电流产生的转矩最大化（Nm/ANm/ANm/A），而非单位视在功率产生的有功最大化（W/VAW/VAW/VA）。在MTPA轨迹上，随着转矩增加，idi_did 负向增加。虽然利用了磁阻转矩，但较大的 idi_did 分量增加了视在功率中的无功部分。
结论：MTPA通常能获得较好的功率因数（0.85-0.95），但并非理论最大值。它是在铜损最小化和转矩最大化之间的权衡，而非PF最大化。

3.3 逆变器容量最优策略：UPF（单位功率因数）控制

UPF控制旨在强制电压矢量与电流矢量同相（ϕ=0\phi = 0ϕ=0），从而使逆变器的容量利用率达到100%。

实现机制 ：控制器根据实时电压方程解算出所需的 idi_did 值，使得 Q=1.5(vqid−vdiq)=0Q = 1.5(v_q i_d - v_d i_q) = 0Q=1.5(vqid−vdiq)=0。这通常要求电机运行在特定的去磁电流点上，以抵消电感的无功效应。
代价分析 ：为了强行拉平功率因数，UPF控制往往需要偏离MTPA轨迹。这意味着为了输出同样的转矩，需要的总电流幅值 IsI_sIs 会比MTPA模式下更大。
效率惩罚 ：IsI_sIs 增大导致铜损（I2RI^2RI2R）增加。因此，UPF是以牺牲电机本体效率（增加发热）为代价，换取逆变器侧容量的节省。
应用场景：UPF策略通常仅用于逆变器容量严格受限、或者对电网侧PF有硬性规定且无前端PFC的场合。

3.4 高速区域的功率因数崩塌与MTPV控制

当电机转速超过基速，进入弱磁（Flux Weakening, FW）区域时，电压达到极限椭圆边界。

深层弱磁的PF行为 ：为了维持电压不超限，必须施加巨大的负 idi_did 去磁。此时，电流矢量主要成分是励磁（去磁）分量，有功分量 iqi_qiq 被压缩。这导致功率因数在高速区迅速下降，甚至降至0.5以下。这种现象被称为"功率因数崩塌"。
MTPV（最大转矩电压比）优化：在深层弱磁区，传统的弱磁轨迹可能并非最优。MTPV控制寻找电压极限椭圆上的最佳工作点，使得在给定电压极限下输出转矩最大。MTPV轨迹实际上是在电压受限条件下对功率因数的一种间接优化，它避免了过度的去磁电流，使得在高转速下的PF优于简单的弱磁控制。

第四章电机本体设计的电磁优化（硬件路径）

控制策略只能在物理极限内进行调节，电机本身的本征功率因数能力（Intrinsic Power Factor Capability）是由电磁设计决定的。要从根本上优化PF，必须在设计阶段处理好电感与磁链的平衡。

4.1 转子拓扑结构的选择：SPM vs. IPM

表贴式（SPM） ：由于永磁体磁导率接近空气，SPM电机的有效气隙很大，导致同步电感 Ld,LqL_d, L_qLd,Lq 很小。
PF优势 ：小电感意味着电枢反应电压降（ωLI\omega L IωLI）很小，反电势 E0E_0E0 主导电压矢量。因此，SPM电机通常具有极高的本征功率因数，容易接近1。
内置式（IPM） ：磁体埋入铁芯，有效气隙小，qqq 轴电感 LqL_qLq 大。
PF挑战 ：大的 LqL_qLq 造成巨大的无功压降。虽然IPM利用了磁阻转矩，但高凸极率（High Saliency）往往伴随着较低的功率因数。
优化方向 ：在IPM设计中，可以通过多层V型 或磁障设计 来压低 LqL_qLq，或者适当增加永磁体用量以提高 ψpm\psi_{pm}ψpm 占比，从而提升PF。

4.2 气隙长度的权衡艺术

气隙长度（ggg）是影响功率因数最敏感的几何参数之一，且其影响具有反直觉性。

感应电机：必须极小化气隙以减小励磁电流，提高PF。
PMSM ：情况恰恰相反。增大气隙 可以显著减小电枢反应电感（Ld,LqL_d, L_qLd,Lq）。
机理：电感减小 →\rightarrow→ 电枢反应电压降减小 →\rightarrow→ 电压矢量偏转角减小 →\rightarrow→ 功率因数提高。
代价：增大气隙会增加磁阻，为了维持同样的空载气隙磁密 BgB_gBg，必须增加永磁体的厚度或用量，显著增加成本。
设计甜点：设计者需在"高PF（大气隙）"与"低磁钢成本（小气隙）"之间寻找平衡。

4.3 绕组形式：分布式 vs. 集中式

分布式绕组（DW）：产生正弦度好的磁动势（MMF），低次谐波含量少，漏感低。
PF表现：由于漏感低，且主电感设计灵活，DW电机通常具有较高的功率因数，适合高性能牵引电机。
分数槽集中绕组（FSCW）：端部短，铜损低，便于制造。
PF陷阱 ：FSCW定子磁动势含有极其丰富的空间谐波。这些谐波不产生平均转矩，只产生脉动转矩和巨大的谐波漏电感。谐波漏抗在高速下产生巨大的无功压降，严重拖累功率因数。
优化：如果必须使用FSCW（为了紧凑性），需通过极槽配合优化（如选取最大公约数大的配合）、不等齿宽设计或转子极弧优化来削弱特定的MMF谐波，降低漏感。

4.4 抑制漏感的设计细节

漏电感（Leakage Inductance）是功率因数的"隐形杀手"，它只消耗无功压降而不做功。

槽漏抗优化：深窄槽虽然利于散热，但会显著增加槽漏抗。优化槽口宽度（Slot Opening）和槽型几何，采用半磁性槽楔，可以在不牺牲太多转矩脉动的情况下降低漏抗。
端部漏抗：优化端部整形工艺，减小端部长度。

第五章系统级权衡：电机优化 vs. 有源前端（AFE）

在工程实践中，必须区分电机功率因数 与电网侧功率因数。

5.1 传统的二极管整流与PFC困境

如果驱动器使用传统的六脉波二极管整流桥，无论电机本体的PF多高，电网侧看到的PF都很低（通常 < 0.9），且含有大量谐波。此时，优化电机本体PF对改善电网侧电能质量毫无帮助，仅能减小电机电缆的电流应力。

5.2 有源前端（AFE）技术的解耦作用

AFE（Active Front End）驱动器采用IGBT整流桥，可以主动控制网侧电流为正弦波且与电压同相。

解耦效应 ：AFE将电网侧PF与电机侧PF完全解耦。网侧可以恒定维持 PF≈1.0PF \approx 1.0PF≈1.0。
系统策略：
方案A（传统）：使用无AFE的驱动器。此时必须花费高昂成本优化电机设计（多用磁钢、大气隙、复杂绕组）以提高电机PF，避免电网罚款和变压器过载。
方案B（现代） ：使用AFE驱动器。此时电机设计可以完全解放，不再受制于PF目标，转而专注于MTPA效率最优 或功率密度最优。虽然AFE成本较高，但可以通过电机成本的降低（少用磁钢、允许FSCW）和系统能效的提升来抵消。

5.3 成本与效益分析

对于大功率系统，方案B往往更具优势。通过AFE解决PF问题，电机可以设计得具有更高的电感（如Vernier电机或高凸极率IPM），从而利用更大的磁阻转矩，提升转矩密度，减小体积。这种"低电机PF + AFE补偿"的架构正在成为高端工业驱动和电动船舶推进的主流选择。

第六章结论与建议

永磁同步电机的功率因数优化是一个跨越材料、几何设计、控制算法与系统架构的多维度工程问题。与感应电机不同，PMSM的功率因数并非定值，而是具有极大的设计自由度与运行可变性。

核心结论：

物理层面 ：电感（特别是 qqq 轴电感和漏感）是限制PMSM高功率因数的主要因素，而反电势是提升基速以下PF的有利因素。
控制层面 ：MTPA 策略虽然不追求单位功率因数，但提供了最佳的系统能效比，是大多数场景的首选。在逆变器容量受限时，可采用UPF 控制，但需接受电机温升增加的代价。在高速区，MTPV控制是维持PF不崩塌的关键。
设计层面 ：若追求极致的电机PF（如无AFE应用），应优先选择SPM转子 、分布式绕组 ，并适当增大气隙。若追求转矩密度，可接受较低的本征PF（如使用IPM或FSCW），并通过系统侧手段补偿。
系统层面 ：随着电力电子成本的下降，采用AFE驱动器 配合高密度（低PF）电机的拓扑结构，在全生命周期成本（TCO）和性能上往往优于单纯追求高PF电机。

工程建议：

对于电动汽车牵引：优先采用IPM电机配合MTPA/MTPV控制。不必强求电机本体的高PF，重点在于通过控制算法在全工况下优化效率图谱（Map）。
对于工业直驱（如风机、传送带）：如果电网侧PF要求严格且不使用AFE，建议采用SPM或低电感设计的IPM，并通过增大有效气隙来提升本征功率因数。
对于伺服系统 ：动态响应优于PF，通常采用 id=0i_d=0id=0 或 MTPA 控制，PF由直流母线电容和PFC电路在网侧解决。

数据附表

表1：不同设计参数变化对PMSM功率因数的影响趋势

参数增加	对电感的影响	对反电势的影响	对功率因数(PF)的影响	物理机制
定子匝数 (NNN)	显著增加 (∝N2\propto N^2∝N2)	线性增加	下降(高速尤甚)	电抗压降 ωLI\omega L IωLI 增长快于反电势，导致电压矢量偏转。
气隙长度 (ggg)	减小	减小 (需更多磁钢补偿)	上升	减小了电枢反应电感，使得电流对磁场的畸变作用减弱。
槽口宽度	减小漏感	无明显影响	上升	降低了槽漏抗压降。
转子凸极率 (ξ\xiξ)	LqL_qLq 增大	无	下降	qqq 轴电感的增大会显著拉大电压与电流的相位差。
磁钢剩磁 (BrB_rBr)	略微减小 (磁饱和)	显著增加	上升(基速下)	增强了主磁场，使反电势在电压构成中占比更高。

表2：PMSM三种主流控制策略的综合对比

特性维度	MTPA (最大转矩电流比)	UPF (单位功率因数)	id=0 控制
核心目标	最小电流产生最大转矩	无功功率为零 (Q=0Q=0Q=0)	线性化转矩控制
电机本体效率	最高(铜损最小)	较低 (需额外去磁电流，铜损增)	中等 (SPM高，IPM低)
逆变器容量利用	较高 (PF ≈0.9\approx 0.9≈0.9)	最高(PF = 1.0)	一般
功率因数	滞后 (0.85 - 0.95)	单位 (1.0)	随负载增加而单调下降
弱磁能力	强	弱 (需切换策略)	弱
典型应用	EV牵引、高性能伺服	并网发电、容量受限驱动	低成本风机水泵