学习Hammerstein-Wiener 模型，以及在回声消除场景中的应用

学习Hammerstein-Wiener 模型，以及在回声消除场景中的应用

• 前言
• [初识Hammerstein-Wiener 的结合过程](#初识Hammerstein-Wiener 的结合过程)
• 什么是Hammerstein-Wiener模型
• • 基本结构：三明治架构
  • [2. 数学表达](#2. 数学表达)
  • [3. 模型优势](#3. 模型优势)
• 在回声消除领域的成功应用
• • [🎯 Hammerstein-Wiener模型应用案例对比](#🎯 Hammerstein-Wiener模型应用案例对比)
  • [📊 关键参数对比](#📊 关键参数对比)
  • [🧮 各案例算法复杂度分析](#🧮 各案例算法复杂度分析)
  • [🚀 技术演进路径](#🚀 技术演进路径)
  • [🎯 总结与选择建议](#🎯 总结与选择建议)
  • 💡项目的启示
• 如何构建Hammerstein-Wiener模型
• • 非线性回声系统的建模
  • Volterra和Hammerstein的关系
  • Hammerstein系统的辨识（标定）
  • • 离线
    • • [分离最小二乘法（Separable Least Squares）](#分离最小二乘法（Separable Least Squares）)
      • [过参数化方法（Overparameterization Method）](#过参数化方法（Overparameterization Method）)
      • [两阶段法（Two-Stage Method）](#两阶段法（Two-Stage Method）)
    • 在线
    • • [加权递推最小二乘（Weighted RLS）](#加权递推最小二乘（Weighted RLS）)
      • [交替RLS（Alternating RLS）](#交替RLS（Alternating RLS）)
      • [变遗忘因子策略（Variable Forgetting Factor）](#变遗忘因子策略（Variable Forgetting Factor）)
      • 双讲鲁棒自适应策略
    • 对于固定腔体回声消除
    • 关键要点
• 参考

前言

Hammerstein-Wiener模型是回声消除领域的瑞士军刀，能处理绝大多数非线性问题。虽然计算和辨识比线性模型复杂，但在以下情况绝对值得：

1. 使用廉价音频硬件（非线性严重）
2. 高音量应用场景（接近饱和区）
3. 专业音频系统（追求极致质量）
4. 汽车、航空等严苛环境

对于固定腔体回声消除问题，如果腔体本身有非线性（如材料非线性），麦克风也可能有非线性，那么HW模型很可能提供最佳解决方案。从历史上看，几乎所有成功的商业回声消除系统，最终都采用了某种形式的HW模型或其变种，忽然对此模型有一种相见恨晚的感觉。而且DS给我检索到了两个3GPP EVS-NNEC和ITU-T G.168 Annex H两个（搜不到）的标准正在制定神经网络和非线性回声消除的行标，这你受得了吗？

初识Hammerstein-Wiener 的结合过程

开篇：故事的开始肯定是Hammerstein（汉默斯坦）这个人名，他是一位德国数学家，于1930年在《数学分析杂志》发表了一篇题为《关于非线性积分方程》的论文，论文提出了非线性积分方程： y ( t ) = ∫ K ( t , τ ) ⋅ f ( τ , x ( τ ) ) d τ y(t) = ∫ K(t,τ)·f(τ, x(τ)) dτ y(t)=∫K(t,τ)⋅f(τ,x(τ))dτ。然后，这个方程和理论继续沉睡了30年。

发展：NASA工程师L. K. Hitz和B. F. Womack在1965年的一份内部报告中，首次将Hammerstein的积分方程离散化为"静态非线性+动态线性"的串联结构，为了简化，他们假设非线性部分无记忆，这是工程化的关键一步。麻省理工学院的K. S. Narendra和J. D. Gallman在1966年的Gallman博士生论文中，提出了分离辨识算法，证明了在持续激励下，模型参数可唯一辨识，至此给出了第一个实用算法。

兴起：Gallman后来去了贝尔实验室，推动了Hammerstein方程进一步的在通信领域长足的进步：

1. 1978年，T. M. Chien提出了Hammerstein模型的LMS自适应算法
2. 1980年，O. Macchi将模型扩展到复数域，用于QAM调制
3. AT&T在长途电话线路中使用该模型进行非线性回声消除

所以有些人认为应该叫"Narendra-Gallman模型，此外，该模型还在控制领域、生物领域等等意想不到的地方取得了辉煌的成就。

突破：1985年，英国学者S. A. Billings和S. Y. Fakhouri做出了关键贡献：证明了Hammerstein模型是Volterra级数的最小参数实现，

提出了基于相关分析的辨识方法，将模型扩展到多输入多输出（MIMO）情况。

与维纳合体：Hammerstein-Wiener模型的诞生源于学术界的一场"融合运动"，

1960年代：Hammerstein模型（非线性-线性）在航天领域成功应用

1970年代：Wiener模型（线性-非线性）在生物医学领域崭露头角

1985年关键会议：IEEE CDC会议上，MIT的D. Westwick和R. Kearney提出："为什么不能同时有输入和输出非线性？"

1987年剑桥大学的Stephen A. Billings（非线性系统辨识的泰斗）发表论文《Identification of Nonlinear Systems - A Survey》，其中正式提出了Hammerstein-Wiener结构，并给出了系统化辨识方法。

1995年MathWorks公司在MATLAB System Identification Toolbox中加入了Hammerstein-Wiener模型辨识工具，使其成为工业界标准。

什么是Hammerstein-Wiener模型

基本结构：三明治架构

Hammerstein-Wiener模型是Hammerstein模型和Wiener模型的串联组合，形成"非线性-线性-非线性"的三明治结构：
输入 u ( t ) → → [ 输入静态非线性 N i n ( ⋅ ) ] → → 中间信号 x ( t ) → → [ 线性动态系统 H ( z ) ] → → 中间信号 v ( t ) → → [ 输出静态非线性 N o u t ( ⋅ ) ] → → 输出 y ( t ) 输入 u(t) →\\→ \bold{[输入静态非线性 N_in(·)]} →\\→ 中间信号 x(t) →\\→ \bold{[线性动态系统 H(z)] } →\\→ 中间信号 v(t) →\\→ \bold{ [输出静态非线性 N_out(·)]} →\\→ 输出 y(t) 输入u(t)→→[输入静态非线性Nin(⋅)]→→中间信号x(t)→→[线性动态系统H(z)]→→中间信号v(t)→→[输出静态非线性Nout(⋅)]→→输出y(t)

2. 数学表达

输入非线性： x ( t ) = f ( u ( t ) ) x(t) = f(u(t)) x(t)=f(u(t))

通常： f ( u ) = c 1 u + c 2 u 2 + c 3 u 3 + . . . f(u) = c₁u + c₂u² + c₃u³ + ... f(u)=c1u+c2u2+c3u3+...

线性动态系统： v ( t ) = H ( z ) ∗ x ( t ) v(t) = H(z) * x(t) v(t)=H(z)∗x(t)

通常用FIR/IIR滤波器表示

输出非线性： y ( t ) = g ( v ( t ) ) y(t) = g(v(t)) y(t)=g(v(t))

通常： g ( v ) = d 1 v + d 2 v 2 + d 3 v 3 + . . . g(v) = d₁v + d₂v² + d₃v³ + ... g(v)=d1v+d2v2+d3v3+...

3. 模型优势

1. 表达能力极强：能描述大多数"温和"的非线性动态系统
2. 物理意义清晰：非线性与线性部分分离，便于理解和解释
3. 辨识相对可行：虽然比单一模型复杂，但有系统化辨识方法

在回声消除领域的成功应用

真实声学回声路径包含多重非线性： 数字信号 → → [ D A C 非线性 ] → [ 功放非线性 ] → [ 扬声器非线性 ] → → [ 空气传播 ( 线性 ) ] → [ 房间反射 ( 线性 ) ] → → [ 麦克风非线性 ] → [ 前置放大非线性 ] → [ A D C 非线性 ] → → 数字信号 数字信号 →\\→ [DAC非线性] → [功放非线性] → [扬声器非线性] →\\→ [空气传播(线性)] → [房间反射(线性)] →\\→ [麦克风非线性] → [前置放大非线性] → [ADC非线性] →\\→ 数字信号 数字信号→→[DAC非线性]→[功放非线性]→[扬声器非线性]→→[空气传播(线性)]→[房间反射(线性)]→→[麦克风非线性]→[前置放大非线性]→[ADC非线性]→→数字信号好巧不巧，这不正合上述的三明治对上号了吗？ 发送端非线性： D A C 、功放、扬声器 → H a m m e r s t e i n 部分 传播路径：空气、房间 → 线性部分 接收端非线性：麦克风、前置放大、 A D C → W i e n e r 部分 发送端非线性：DAC、功放、扬声器 → Hammerstein部分\\ 传播路径：空气、房间 → 线性部分\\ 接收端非线性：麦克风、前置放大、ADC → Wiener部分 发送端非线性：DAC、功放、扬声器→Hammerstein部分传播路径：空气、房间→线性部分接收端非线性：麦克风、前置放大、ADC→Wiener部分

DS给出了几家的成功应用，整理成表格如下：

🎯 Hammerstein-Wiener模型应用案例对比

特性维度	Polycom SoundStation (1998)	宝马iDrive语音控制 (2005)	苹果AirPods Pro (2019)	Zoom背景噪声抑制 (2020)
核心挑战	小型会议室非线性回声	汽车极端环境噪声和失真	微型扬声器严重非线性，功耗限制	海量廉价设备兼容性问题
应用场景	会议室电话系统	车载语音控制系统	真无线耳机通透模式	视频会议软件
非线性处理	3阶多项式输入非线性 + 查找表输出非线性	5阶多项式+死区补偿输入 + 动态压缩输出	3阶分段多项式输入 + 个性化耳道补偿输出	设备指纹识别 + 通用非线性补偿
线性部分	512阶FIR滤波器	自适应FIR滤波器（长度可变）	32阶稀疏FIR（仅8个活跃抽头）	云端可配置FIR参数
辨识方法	离线标定，出厂预置	在线自适应 + 离线标定基础模型	个性化标定（每用户一次）	设备数据库 + 云端模型推送
计算复杂度	中等（1998年DSP水平）	高（汽车级处理器）	极低（H1芯片专用硬件）	可变（云+端协同）
创新点	首次商业大规模应用HW模型	环境自适应双模式切换	个性化耳道响应补偿	海量设备自动识别与适配
性能提升	ERLE提升15dB	语音识别准确率从65%→92%	微型扬声器失真降低12dB	廉价设备回声抑制提升10-20dB
功耗要求	无特别要求	中等（车载电源）	极严格（耳机电池）	客户端中等，云端无限制
商业影响	占据70%会议电话市场	确立高端车载语音标准	通透模式成为行业标杆	疫情期间用户增长300倍
技术遗产	G.167标准推荐模型	车载AEC标准架构	真无线耳机非线性补偿范式	大规模设备兼容性解决方案

📊 关键参数对比

参数	Polycom	宝马	苹果	Zoom
输入非线性阶数	3阶	5阶	3阶（分段）	设备相关
FIR滤波器长度	512	128-512可变	32（稀疏）	64-256
输出非线性形式	查找表	动态范围压缩	个性化查找表	软饱和函数
更新频率	永不	实时自适应	每用户一次	设备首次识别
处理延迟	20ms	<10ms	<5ms	网络相关
内存占用	8KB	16KB	2KB	云端为主
标定时间	15分钟	工厂标定+在线学习	30秒/用户	自动识别

🧮 各案例算法复杂度分析

操作	Polycom (MOPS)	宝马 (MOPS)	苹果 (MOPS)	Zoom客户端 (MOPS)
输入非线性计算	0.5	1.2	0.3	0.8
FIR滤波	5.1	2.5	0.6	1.5
输出非线性计算	0.3	0.8	0.2	0.5
参数更新	0	2.0	0.1	0.3
总计	5.9	6.5	1.2	3.1
适用处理器	TI C54x	Freescale MPC	Apple H1	Intel i5

注：MOPS = 百万次操作/秒，基于16kHz采样率估算

🚀 技术演进路径

发展阶段	代表技术	核心突破	局限性
第一代 (1990s)	Polycom HW模型	非线性回声建模可行性	固定参数，无自适应
第二代 (2000s)	宝马自适应HW	环境自适应，多模式切换	计算复杂度高
第三代 (2010s)	苹果轻量化HW	极致优化，个性化校准	需要用户校准
第四代 (2020s)	Zoom云+端HW	海量设备兼容，自动适配	依赖网络，隐私顾虑

🎯 总结与选择建议

项目特点	推荐借鉴案例	核心采用技术	避免的坑
固定安装，环境稳定	Polycom	离线精密标定 + 固定HW模型	避免过度自适应增加复杂度
资源受限，低功耗	苹果AirPods	分段多项式 + 稀疏FIR	避免高阶多项式，注意数值稳定性
需要应对慢变化	宝马iDrive	基础固定模型 + 慢自适应校正	避免快速自适应引起抖动
面对多种可能配置	Zoom	设备特征识别 + 模型切换	避免单一模型应对所有情况

💡项目的启示

启示要点	具体建议	预期效果
从简单开始	先实现Hammerstein模型，再扩展到HW	快速验证，渐进优化
考虑实际限制	根据处理器能力选择模型复杂度	保证实时性，避免过拟合
利用离线标定	对固定腔体做精密标定，减少在线计算	获得最佳性能，降低功耗
设计可扩展架构	预留自适应模块接口，方便未来升级	长期维护性，适应变化
性能监控	实现ERLE等指标实时监测	及时发现问题，优化参数

如何构建Hammerstein-Wiener模型

非线性回声系统的建模

首先要回顾一下非线性回声过程的建模，引用Nonlinear Acoustic Echo Cancellation网站上的一张图，比较形象：

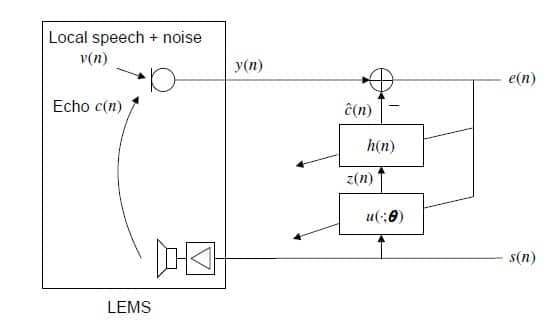
其中用 u ( . ; θ ) u(.;\theta) u(.;θ)建模非线性过程。这个模型是非线性在前的，应该适配Hammerstein-Wiener模型。文中还归类了非线性为有记忆和无记忆的：

有记忆的：扬声器的非线性记忆效应，这是因为高保真扬声器中电声线圈系统的时间常数大于采样间隔所致。

无记忆的：无记忆非线性通常是由于低成本硬件的温度漂移导致扬声器与麦克风之间的采样率失配，或由这类系统的饱和效应所引起。
Volterra AEC一文还对非线性产生的来源做了剖析，认为主要的来源点是喇叭本身，笔者羡慕作者没做过便宜的产品，如果腔体耦合严重，甚至有的将mic和spk共处一室，踏马德就是声学灾难，卷无可卷的生态。

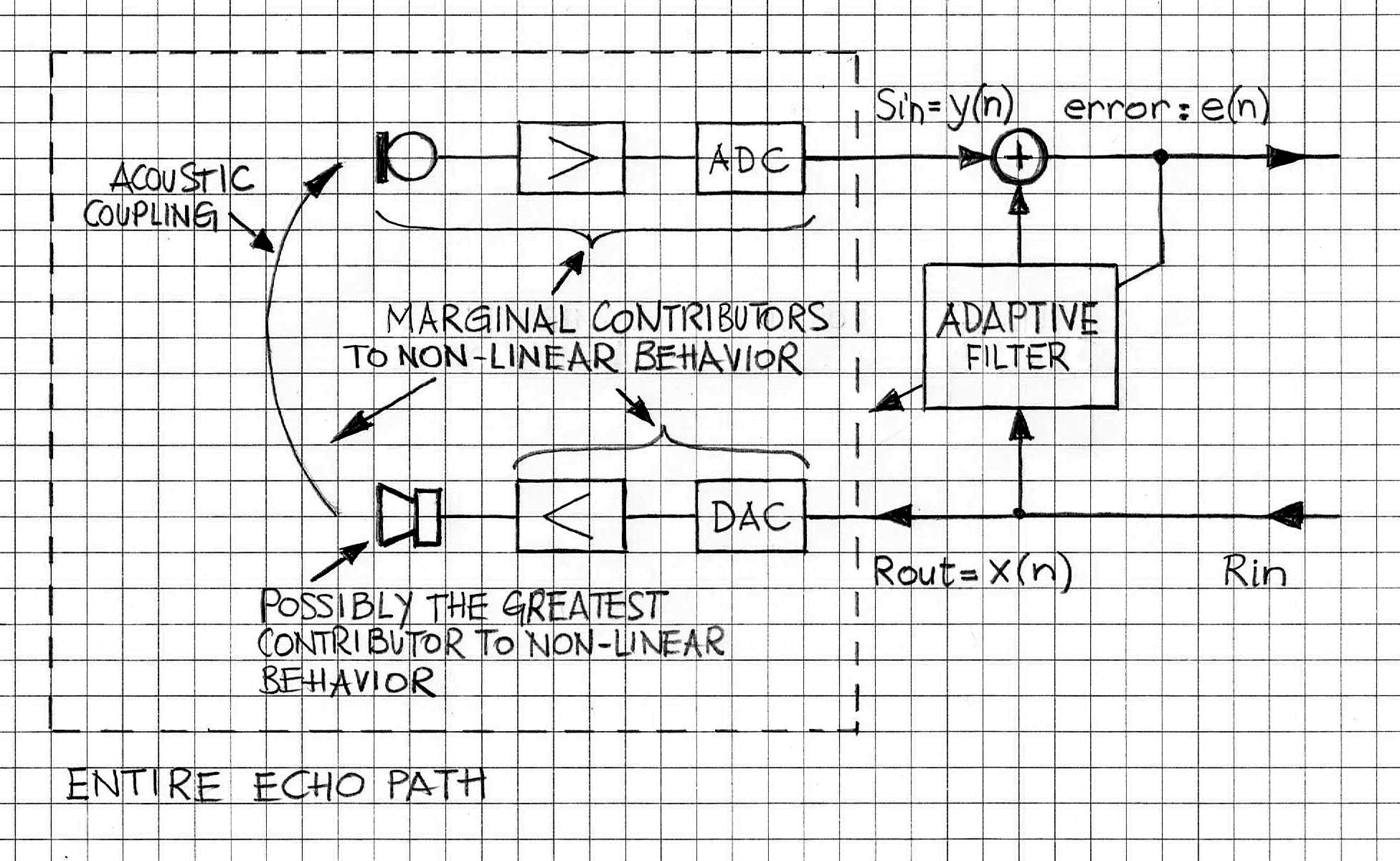
吐槽归吐槽，实际场景可以将非线性和线性设计成一个级联（cascaded）系统，那么就可以如下图

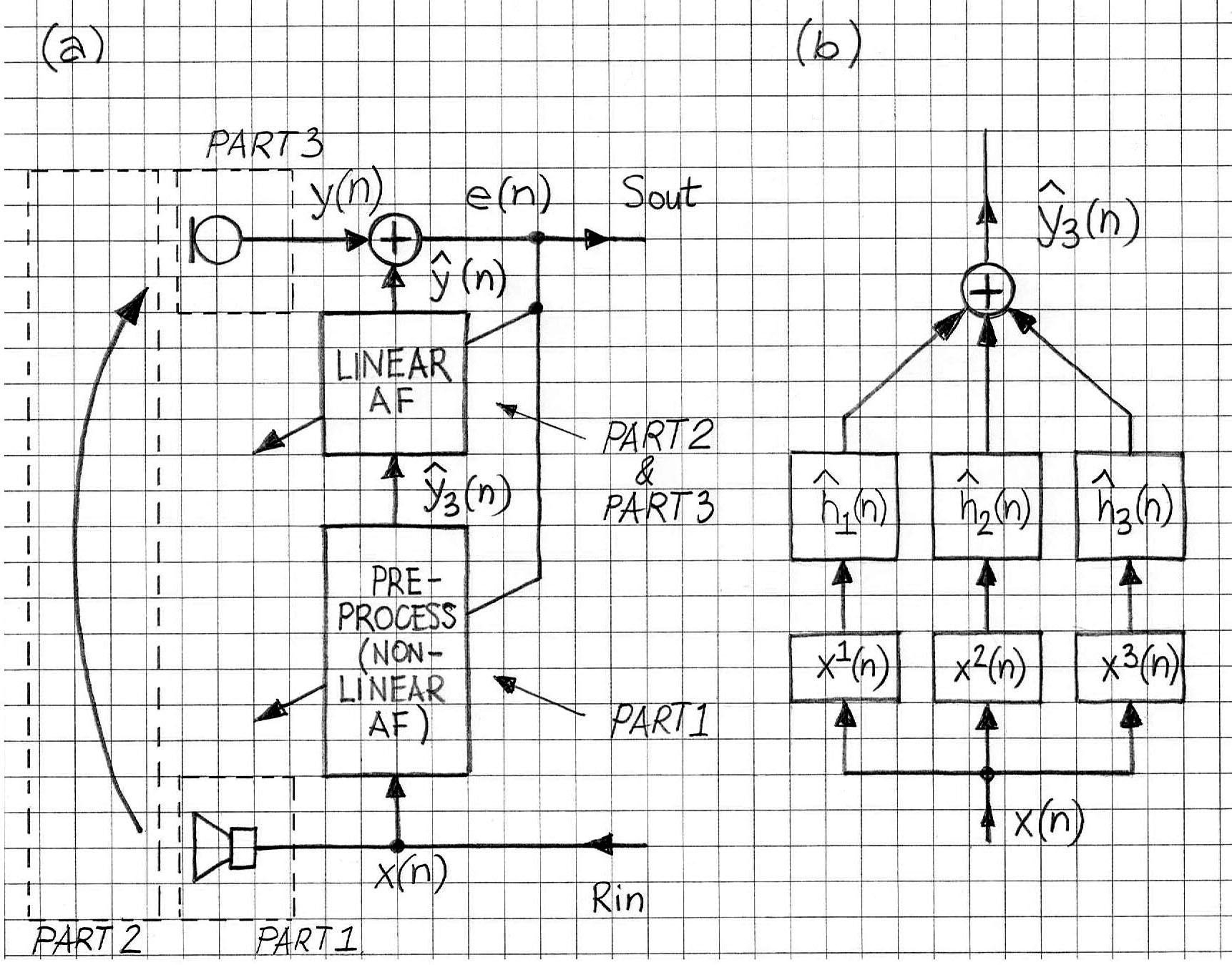
或者这样（来自论文Robust and low-cost cascaded non-linear acoustic echo cancellation）

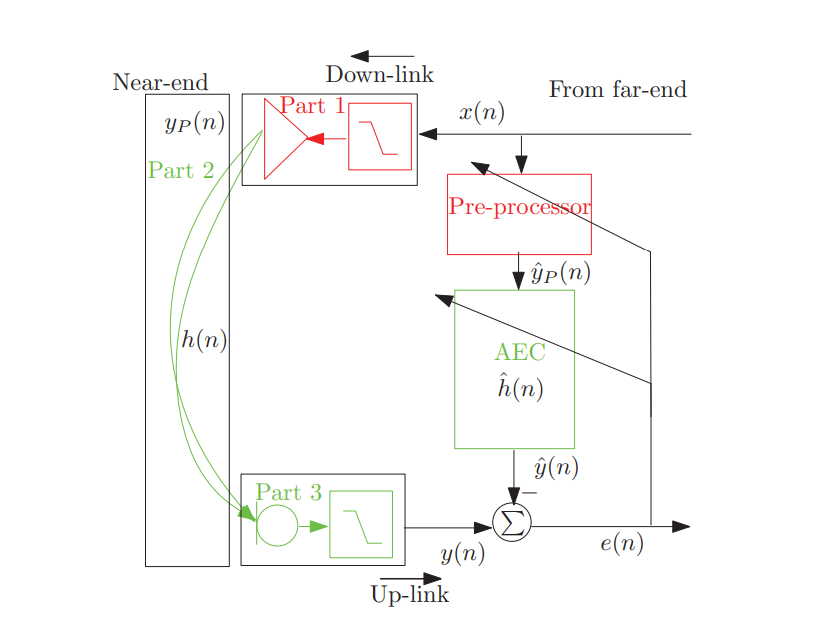
上面三个图的pre-processor是自适应的，volterra形式，Hammerstein我认为是静态估计，实时系统不会再改变了。正如Nonlinear Acoustic Echo Cancellation文末总结的，翻译一下：

在设计非线性声学回声消除器时，最紧迫的问题是使用何种非线性模型，以及将该模型置于回声路径中的何处。使问题复杂化的是这样一种观念：回声路径本身可能并非完全线性的。若假设其为线性，则可以选择将非线性模型置于标准FIR自适应滤波器之前、之后或直接替代它。模型的放置位置应考虑到你试图捕捉的非线性类型。例如，扬声器线圈的模型应置于FIR滤波器之前，而麦克风削波的模型则应置于其后。

在识别非线性特性方面，神经网络提供了最大的灵活性。如文献[3]所示，图3所示的时延前馈网络既可以单独使用，也可以与由NLMS算法适配的标准FIR滤波器级联使用。此外，文献中阐述了多种学习算法，可单独或组合使用。借助神经网络，可能性几乎是无限的。这里请DS 给了建模基本思路如下：

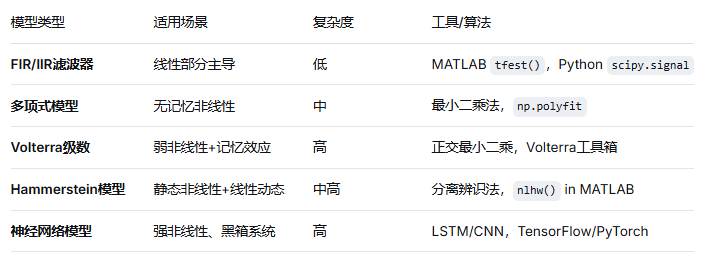
而在回声消除过程中，与维纳模型联合使用的场景不多，那二者如何取舍呢？参考下图

对于腔体非线性，Hammerstein模型通常更合适，因为非线性通常发生在能量输入阶段（如驱动单元）。

Volterra和Hammerstein的关系

一言以蔽之：Hammerstein模型是Volterra级数的最小参数实现，因为它强制所有非线性都发生在同一时刻，不同时刻的输入只能线性叠加。volterra的级数表达 y ( t ) = h 0 + Σ h 1 ( τ ) u ( t − τ ) + Σ Σ h 2 ( τ 1 , τ 2 ) u ( t − τ 1 ) u ( t − τ 2 ) + . . . y(t) = h₀ + Σ h₁(τ)u(t-τ) + ΣΣ h₂(τ₁,τ₂)u(t-τ₁)u(t-τ₂) + ... y(t)=h0+Σh1(τ)u(t−τ)+ΣΣh2(τ1,τ2)u(t−τ1)u(t−τ2)+...Hammerstein的数学表达 y ( t ) = H [ f ( u ( t ) ) ] y(t) = H[ f(u(t)) ] y(t)=H[f(u(t))]举例：一个记忆长度为3，非线性阶数为3的系统，Volterra级数要考虑所有可能的乘积组合：
u ( t ) , u ( t − 1 ) , u ( t − 2 ) 一阶： 3 项 u ( t ) 2 , u ( t ) u ( t − 1 ) , u ( t ) u ( t − 2 ) , u ( t − 1 ) 2 , u ( t − 1 ) u ( t − 2 ) , u ( t − 2 ) 2 二阶： 6 项 u ( t ) 3 , u ( t ) 2 u ( t − 1 ) , . . . 三阶：更多项 u(t), u(t-1), u(t-2) 一阶：3项\\ u(t)², u(t)u(t-1), u(t)u(t-2), u(t-1)², u(t-1)u(t-2), u(t-2)² 二阶：6项\\ u(t)³, u(t)²u(t-1), ... 三阶：更多项 u(t),u(t−1),u(t−2)一阶：3项u(t)2,u(t)u(t−1),u(t)u(t−2),u(t−1)2,u(t−1)u(t−2),u(t−2)2二阶：6项u(t)3,u(t)2u(t−1),...三阶：更多项

Hammerstein模型只有： f ( u ) = c 1 u + c 2 u 2 + c 3 u 3 3 个参数 y ( t ) = a 0 x ( t ) + a 1 x ( t − 1 ) + a 2 x ( t − 2 ) 3 个参数 f(u) = c₁u + c₂u² + c₃u³ 3个参数\\ y(t) = a₀x(t) + a₁x(t-1) + a₂x(t-2) 3个参数 f(u)=c1u+c2u2+c3u33个参数y(t)=a0x(t)+a1x(t−1)+a2x(t−2)3个参数

Hammerstein模型可以看成一个特殊的Volterra级数：
一阶核： h 1 ( τ ) = c 1 h ( τ ) 二阶核： h 2 ( τ , τ ) = c 2 h ( τ ) ，其他为 0 （只在 τ 1 = τ 2 有值） 三阶核： h 3 ( τ , τ , τ ) = c 3 h ( τ ) ，其他为 0 （只在 τ 1 = τ 2 = τ 3 有值） 一阶核：h₁(τ) = c₁h(τ) \\ 二阶核：h₂(τ,τ) = c₂h(τ)，其他为0（只在τ₁=τ₂有值）\\ 三阶核：h₃(τ,τ,τ) = c₃h(τ)，其他为0（只在τ₁=τ₂=τ₃有值） 一阶核：h1(τ)=c1h(τ)二阶核：h2(τ,τ)=c2h(τ)，其他为0（只在τ1=τ2有值）三阶核：h3(τ,τ,τ)=c3h(τ)，其他为0（只在τ1=τ2=τ3有值）Hammerstein模型强制Volterra核有对角化结构：

Hammerstein系统的辨识（标定）

可分为离线和在线两种方法

离线

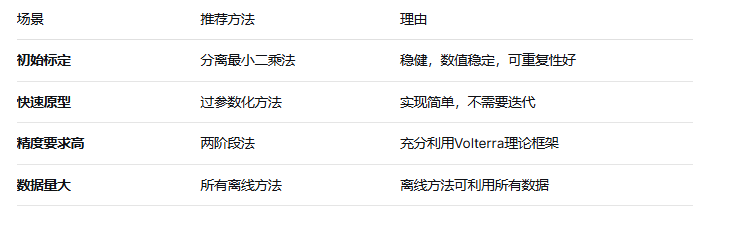
分离最小二乘法（Separable Least Squares）

过参数化方法（Overparameterization Method）

两阶段法（Two-Stage Method）

在线

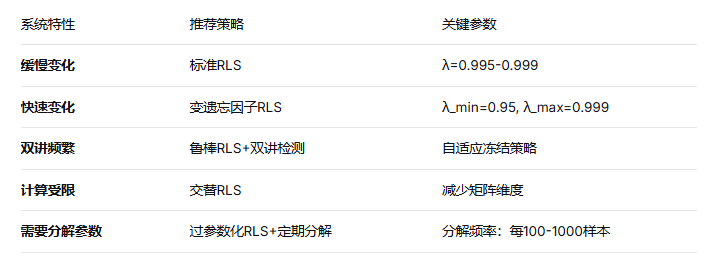
加权递推最小二乘（Weighted RLS）

交替RLS（Alternating RLS）

变遗忘因子策略（Variable Forgetting Factor）

双讲鲁棒自适应策略

对于固定腔体回声消除

1. 离线精确标定

2. 在线自适应微调

3. 性能优化

    	监控ERLE，动态调整遗忘因子
    	
    	检测双讲，冻结或减缓自适应
    	
    	定期检查参数变化，防止发散

关键要点

离线辨识：分离最小二乘法最稳健，过参数化方法最直接

在线辨识：RLS系列算法是标准，变遗忘因子提高鲁棒性

实际应用：总是结合离线标定和在线微调

监控调试：必须实现收敛监控和故障检测

参考

https://www.itu.int/rec/T-REC-G.167-199303-W/en
有色噪声干扰下 Ｈａｍｍｅｒｓｔｅｉｎ非线性系统两阶段辨识
非线性系统辨识：非线性 ARX 和 Hammerstein-Wiener
Efficient Nonlinear Acoustic Echo Cancellation by Partitioned-Block Significance-Aware Hammerstein Group Models
A Cascaded Kernel-Based Approach for Nonlinear Acoustic Echo Cancellation
【Hammerstein模型的级联】快速估计构成一连串哈默斯坦模型的结构元素研究（Matlab代码实现）
Volterra AEC
Non-Linear AEC
Nonlinear acoustic echo cancellation using low-complexity low-rank recursive least-squares algorithms
Nonlinear Acoustic Echo Cancellation
Nonlinear Acoustic Echo Cancellation: Topics in Acoustic Echo and Noise Control