目录
[1. 与eigen相关的词源](#1. 与eigen相关的词源)
[1.1 eigen](#1.1 eigen)
[1.2 eigenvalue, eigenvfunction, eigenvector及相关术语](#1.2 eigenvalue, eigenvfunction, eigenvector及相关术语)
[1.3 词源总结](#1.3 词源总结)
[2. 特征向量和特征值的数学意义](#2. 特征向量和特征值的数学意义)
[3. 线性变换简述](#3. 线性变换简述)
[3.1 从旋转来理解线性变换](#3.1 从旋转来理解线性变换)
[3.1.1 2维空间中旋转矩阵的推导](#3.1.1 2维空间中旋转矩阵的推导)
[3.1.2 3维空间中旋转矩阵的推导](#3.1.2 3维空间中旋转矩阵的推导)
[3.1.3 二维和三维旋转矩阵的属性](#3.1.3 二维和三维旋转矩阵的属性)
[3.2 为什么用矩阵来表示线性变换](#3.2 为什么用矩阵来表示线性变换)
[3.2.1 使用矩阵的关键理由](#3.2.1 使用矩阵的关键理由)
[3.2.2 如何利用矩阵进行线性变换](#3.2.2 如何利用矩阵进行线性变换)
[3.3 线性变换的正式定义](#3.3 线性变换的正式定义)
[3.3 线性变换与矩阵的关系](#3.3 线性变换与矩阵的关系)
[4. 线性变换与特征值的关系](#4. 线性变换与特征值的关系)
[4.1 特征值存在的情况](#4.1 特征值存在的情况)
[4.2 特征值不存在的情况(在实数场中)](#4.2 特征值不存在的情况(在实数场中))
[4.3 如何理解(从几何和代数角度)](#4.3 如何理解(从几何和代数角度))
[5. 如何求得矩阵的特征值(线性变换的特征值)](#5. 如何求得矩阵的特征值(线性变换的特征值))
1. 与 eigen相关的词源
eigen 这个词(或构词前缀) 中古荷兰语 eigen ,来自古荷兰语"*eigan"(to own)("拥有")(注:*号表示后世人们根据一些资料记录的发音创造的拼写),这又来自来自原始西日耳曼语(Proto-West Germanic)"*aigan",这个词又来自原日耳曼语 "aiganą" 。 也就是说,这个词最初是来自日耳曼语的。
eigen基本词义:
(1) own, private(自有的,私有的)
(2) characteristic**,** typical**,**specific(特征的,典型的,特有的)。
1.1 eigen
数学中 eigen 这个术语与 David Hilbert(1862-1943)有关,尽管他可能一直在遵循声学上与 Eigentöne 相同的结构(参见 《H.L.F.Helmholtz的单调感觉理论》 (H.L.F.Helmholtz Lehre von dentonempfindungen))。Eigenfunktion 和 Eigenwert 出现在Hilbert关于积分方程的第一篇通讯《线性积分方程一般理论基础》"Grundzüge einer allgemeinen Theorie der Linearen Integralgleichungen"中(Nachrichten von d. Königl. Ges. d. Wissensch. zu Göttingen (Math.-physik.Kl.)(1904)(第 49-91而))。(1904-1910 年的通信被收集为Grundzüge einer allgemeinen Theorie der Linearen Integralgleichungen(线性积分方程一般理论基础)1912)。在 Whittaker & Watson 的《现代分析课程》(Course of Modern Analysis)中,"Eigenfunktion"转译为"autofunction"。Eigenvektor出现在 Courant & Hilbert 的《数学物理方法》(Methoden der Mathematischen Physik) (1924) 中对有限维情况的阐述中。
Hilbert 最初的出发点是一个非齐性积分方程,其参数为λ ,对应的矩阵为 (I - λA )x = y 。Hilbert将产生这些方程齐性版本的一个非零解的 λ 值称为特征值(德语 Eigenwerte);它们是A 的特征根 (characteristic或latent )之倒数。Courant & Hilbert (1924) 使用κ表示"特征数 (characteristiche Zahl)",λ = (1/κ)表示"特征值 (Eigenwert)";Lichnerowicz(上文)给出了法语的对应表述。"Eigenwert"在J. von Neumann的《Hermitescher泛函算子的一般特征值理论》(Allgemeine Eigenwerttheorie Hermitescher Funktionaloperatoren)(Math.Ann.102(1929)第49-131页)中以不同的方式使用:"Eigenwert是一个数,对于该数,存在一个函数f ≠ 0,使得 Rf = λf ,那么它就是一个特征函数 (Eigenfunktion)。"这成为主流用法,以至于到 1946 年,H. & B. Jeffreys(数学物理方法)将特征值(eigenvalue)视为特征值(characteristic value)和特征根(latent root)的同义词。
20世纪20年代矩阵力学(matrix mechanics)的发展推动了特征值(eigen)术语的使用,因为这一新理论是用Hilbert及其学派的语言表述的。参见M. Born, W.Heisenberg和P. Jordan合著的《量子力学II 》(Zur Quantenmechanik II)( Zeitschrift für Physik,第35卷,1926年,第557-615页)第三章。[英文译本及注释收录于B.L.van der Waerden编辑的《量子力学文献选集》(Sources of Quantum Mechanics)(Dover 出版社,1968年)。]
通过《牛津英语词典》(OED)和JSTOR数据库,我们可以追溯"eigen"一词及其相关术语在英语物理学中的演变过程。在1926年,P. A. M. Dirac在论文《关于量子力学的理论》(On the Theory of Quantum Mechanics)(发表于《皇家学会会刊A辑》(Proc. Royal Soc. A ),第112卷,第661-677页)中写道:"一组可以称为特征函数 (eigenfunction)的独立解"(OED)。"特征值 "(Eigenvalue)一词出现在A.S.Eddington于1927年7月23日写给《自然(Nature)》杂志的一封信中,在信中开头写道:"在那些......试图对Schrödinger[ʃróudiŋə]波动力学有一个大致了解的人中,肯定有许多人发现自己的数学基础不足以理解他的第一个重要问题------确定氢原子的特征值 (eigenvalue)和特征函数(eigenfunction)"(OED)。"特征向量"(Eigenvector)一词出现在R. Brauer和H.Weyl合著的《n维空间中的旋量》(Spinors in n Dimensions)(发表于《美国数学杂志》(Amer. J.Math.),第57卷,1935年,第425-449页)中(JSTOR)。虽然" eigenvalue "," eigenfunction "和" eigenvector "都是德语原文的翻译,但Dirac在《量子力学原理》(Principles of Quantum Mechanics)(1930年,第35页)中提出的"特征态"(eigenstate)是一个新的术语,标志着"eigen"作为一个完全独立的英语词素的出现。"特征态"翻译成德语为Eigenzustand 。
" Proper "(特有的,专有的) 一直是" eigen "的标准英语译法 ------因此,在19世纪,Helmholtz的"Eigentöne"译为"proper tones"。"Proper values"(特征值)和"proper functions"(特征函数)出现在von Neumann的英文著作中,例如在他与S. Bochner合著的《关于算子微分方程的紧致解》(On Compact Solutions of Operational-Differential Equations. I),发表于《数学年刊》(Annals of Mathematics),第二辑,第36卷(1935年),第255-291页。尽管如此,在他1932年出版的《量子力学的数学基础》 (Mathematische Grundlagen der Quantenmechanik)的1949年英文译本中,却使用了" eigenvalue**"(特征值)一词。** Dirac (《量子力学原理》(Principles of Quantum Mechanics))反对使用"proper"这一术语(而赞成使用"eigen"),理由是" proper "在物理学中还有其他含义。
Paul Halmos(见上文)沿用了von Neumann的英文著作中的术语,并在他广为使用的《有限维向量空间》(Finite Dimensional Vector Spaces)(1958年)一书中使用了"proper value"(特征值)。然而,Halmos在《Hilbert空间问题集》(A Hilbert Space Problem Book)(1967年,第x页)中承认了自己的不足:
"For many years I have battled for proper values, and against the one and a half times translated German-English hybrid that is often used to refer to them. I have now become convinced that the war is over, and eigenvalues have won it; in this book I use them."(多年来,我一直在为正确的术语而奋斗,反对那种经过一次半翻译的德语-英语混合词,这种混合词经常用来指代这些术语。现在我确信这场斗争已经结束,eigenvalue这个术语最终胜出;因此,本书中我将使用这个术语。)
2016年,Jan Peter Schäfermeyer写道:
"Some time ago I researched the history of the power and related methods to compute eigenvectors and found out that these methods were used first for differential and integral equations, before they were used for the matrix eigenvalue problem. Here are the sources, mostly in German.( 前段时间,我研究了幂法以及相关的特征向量计算方法的历史,发现这些方法最初是用于求解微分方程和积分方程的 ,之后才应用于矩阵特征值问题。以下是一些参考资料,大部分是德语的。)
An interesting aside, that might be of interest for your webpage, concerns the nomenclature of eigenvalues and eigenfunctions, terms that were quickly adopted in the German literature after Hilbert had proposed them in 1904. Before that, I haven't seen any particular names for these entities. Schwarz simply speaks of a function w and a number c. (一个有趣的题外话,或许对你的网页有所帮助,是关于特征值和特征函数的命名问题。这些术语在Hilbert于 1904 年提出后很快就被德国文献所采用。在此之前,我没有看到任何专门用来称呼这些概念的名称。Schwarz只是简单地用函数 w 和数字c 来指代它们。)
The French were more inventive: Picard in two papers, Comptes Rendus 117 (1893), and C.R. 118 (1894), speaks of "points singuliers" and "valeurs singulieres," but also has no particular name for eigenfunctions(法国人更具创造力:Picard在两篇论文(发表于《法国科学院院刊》第117卷(1893年)和第118卷(1894年))中提到了"奇点"和"奇值",但他也没有为特征函数起特定的名称):
Poincare proposes the names "nombres caracteristiques" and "fonctions harmoniques" in an 1894 paper, and in 1896 "fonctions fondamentales. ( Poincare在 1894 年的一篇论文中提出了"nombres caracteristiques"和"fonctions Harmoniques"的名称,并在 1896 年提出了"fonctions foldamentales"的名称。)
And in the English literature I have found the terms "characteristic numbers" and "characteristic functions" used by Bocher in his 1909 book on integral equations.( 在英文文献中,我发现Bocher在他1909年关于积分方程的著作中使用了"characteristic numbers"和"characteristic functions"这两个术语。)"
1.2 eigenvalue,eigenvfunction, eigenvector及相关术语
"几乎所有形容词 proper , latent , characteristic , eigen 和 secular 与名词 root , number 和 value 的组合都在文献中用来指代我们所谓的特征值" (P. R. Halmos,《有限维向量空间》(Finite Dimensional Vector Spaces)(1958,第102页))。更令人困惑的是,特征值及其倒数都具有重要意义 :在 A. Lichnerowicz 的《线性代数与分析》(Algèbre et analyse linéaires)(1947)中,valeur caractéristique 和 valeur propre 互为倒数,但其英文译本(1967)却使用了 eigenvalue 和 proper value , 这两个词都源自同一个德语单词 Eigenwert 。 这些形容词也与其他类型的名词组合使用,包括方程、解、函数和向量。这些术语的演变贯穿代数、分析、力学以及经典物理学和量子物理学等领域。
现代谱理论的阐述通常从矩阵 A 开始,并将特征值 λ 和特征向量 x 一起引入值或特征向量方程 Ax = λx :任何满足此方程且 x 不为零的 λ 都是特征值 ,相应的 x 则是特征向量。方程 (A -- λI )x = 0 存在非零解 x 的条件是 ( A -- λI ) 的行列式为零,即某个多项式的根具有重要意义。这种有限维情况用来启发对微分方程和积分方程的处理,这些方程涉及无限维空间,其中向量现在是一个函数。历史发展顺序大致与此相反。源自天体力学微分方程的多项式方程首先出现,大约在 1780 年;然后,该方程在大约 1830 年用行列式表示;接着,该方程在大约 1880 年与矩阵联系起来;之后,在大约 1900 年开始研究积分方程;最终,从值或向量方程开始的现代主题顺序在大约 1940 年确立。(基于 Kline 第 29、33、45 和 46 章以及 Hawkins (1975 和 1977)。
"secular"(长期或特征 )一词的早期(但并非最早)用法出现在Jacobi的著名论文中,他在该论文中引入了特征值 算法。该术语(牛津英语词典释义为"持续漫长岁月(continuing through long ages)")让人想起谱理论的起源之一是Laplace和Langrage研究的太阳系长期行为问题。参见 Hawkins (1975)。Cauchy在1829年发表的论文中证明了对称行列式的根是实数,该论文的标题是"关于确定行星运动长期不等式的方程"(Sur l'équation à l'aide de laquelle on détermine les inégalités séculaires des mouvements des planétes);这仅仅表明Cauchy意识到他的问题,即在 的约束条件下选择 x 使
最大化(使用现代记法),会得到一个类似于天体力学中研究的方程。Sylvester的论文标题"关于行星理论中长期不等式的方程"(见下文)在内容上更具误导性。在这种传统下,Courant和Hilbert在《数学物理方法》(Methoden der Mathematischen Physik)(1924)中的"Säkulärgleichung"以及 E. T. Browne 在《美国数学杂志》(American Journal of Mathematics)52卷(1930),843-850页发表的论文"关于长期方程根的分离性质(On the Separation Property of the Roots of the Secular Equation)"中的"secular equation"都指的是对称矩阵的特征方程 。"secular equation"(长期方程 或特征方程 )一词出现在现代数值线性代数文献中。
这些特征术(characteristic terms)语源自 Augustin Louis Cauchy (1789-1857),他引入了术语 l'equation caractéristique,并在他的"Mémoire sur l'integration des équations linéaires"中研究了其根源(Exercises d'analysis et de physical mathématique, 1, 1840, 53 = Oeuvres, (2), 11, 76 (Kline,第 76 页) 801)。Frobenius在他关于矩阵的基础论文《关于线性替换和双线性型》(Über Lineare Substitutionen und bilineare Formen)中介绍短语"die Charakteristische Defineante"时,提到了这本回忆录《纯粹数学和应用数学》(für die reine und angewandte Math.(1874), 84, 1-63) 。在《天体力学的新方法》(Les méthodes nouvelles de la mécanique céleste (1892)) 中, Poincaré 写到了关于特征指数 (exposants (exponents) caractéristiques) 的内容。
JSTOR 上的文献显示,"characteristic"一词及其相关概念家族进一步扩展,并传播到英语中:例如,G. D. Birkhoff 在其论文《常线性微分方程的边值问题和展开问题》(Boundary Value and Expansion Problems of Ordinary Linear Differential Equations)(Trans. American Mathematical Society, 9, (1908), 373-395)中使用了"特征值"(characteristic value);H.Hilton 在其论文《某些齐性线性变换的性质》(Properties of Certain Homogeneous Linear Substitutions)(Annals of Mathematics, 2nd Ser., 15, (1913-1914) 195-201)中使用了"特征根"(characteristic root);W. D. A. Westfall 在其论文《广义Green函数的存在性》(Existence of the Generalized Green's Function)(Annals of Mathematics, 2nd Ser., 10, (1909), 177-180)中使用了**"特征解"** (characteristic solution);J. W. Alexander 在其论文《关于协变张量的类》(On the Class of a Covariant Tensor)(Annals of Mathematics, 2nd Ser., 28, (1926-1927), 245-250)以及 F. D. Murnaghan 和 A. Wintner 在其论文《正交变换下实矩阵的规范形式》(Canonical Form for Real Matrices under Orthogonal Transformations)(Proceedings of the National Academy of Sciences of the United States of America, 17, (1931), 417-420)中使用了**"特征向量"**(characteristic vector)。C. C. MacDuffee 的经典著作《矩阵理论》(Theory of Matrices)(1933)使用了特征根(characteristic root)、特征函数和特征方程,但没有使用特征向量。
"latent"这一概念由James Joseph Sylvester(1814-1897)在其1883年发表的论文《关于行星理论中长期不等式的方程》(On the Equation to the Secular Inequalities in the Planetary Theory)中提出,该论文发表于《哲学杂志》(Phil. Mag.)第16卷第267页,并收录于其《数学论文集》(Coll Math Papers)第四卷第110页。
"It will be convenient to introduce here a notion (which plays a conspicuous part in my new theory of multiple algebra), viz. that of the latent roots of a matrix -- latent in a somewhat similar sense as vapour may be said to be latent in water or smoke in a tobacco-leaf. (在此引入一个概念将会很方便(这个概念在我新的多元代数理论中扮演着重要角色),即矩阵的特征根------这里的"特征"一词的含义与水中的水蒸气或烟叶中的烟雾的"潜藏"含义有些类似。)"
Sylvester的论文《关于泛代数世界中的三条运动定律》(On the Three Laws of Motion in the World of Universal Algebra)( Johns Hopkins University Circulars,第3卷,1884年)中包含了"同余定律......该定律断言,矩阵的特征根遵循对矩阵进行的任何函数运算的规律,且不涉及任何其他矩阵的作用。"(《 Sylvester数学论文集》(Coll Math Papers),第四卷,第146页)。Sylvester也使用了"特征方程 (latent equation)"一词(《泛代数原理讲座》(Lectures on the Principles of Universal Algebra),American J. of Math. VI (1884), 216),(《Sylvester数学论文集》(Coll Math Papers),IV, 208 )。"特征向量( latent vector )"一词出现得较晚,可能直到1937年A. C. Aitken发表的论文《实用数学研究II:矩阵特征根和特征向量的计算》(Studies in Practical Mathematics II. The Evaluation of the Latent Roots and Latent Vectors of a Matrix)( Proc. Royal Soc. Edinburgh, 57, 269-304. Previously H.Turnbull & Aitken)才出现。此前,H. Turnbull和Aitken(《规范矩阵理论》(Theory of Canonical Matrices),1932年)使用了"特征点(latent point)"一词,并将其归功于Sylvester 。
1.3 词源总结
前缀"eigen-"源自德语单词 eigen,意为"据有的(own)、专有的(proper)、特征的(characteristic)或自有的(self)",该词被引入英语,用于数学术语 ,例如特征向量/特征值 。它描述了线性变换的一个基本固有属性 ,以表明变换后的向量只是原向量的缩放版本 (即其"自身"的倍数 ),方向保持不变。这个术语由数学家 David Hilbert于1904年左右引入线性代数领域。
本质上,特征向量是指在应用线性变换后仍然保持在自身张成的空间内(方向不变)的向量,只是被相应的特征值进行了缩放,从而体现了其"自身"或"固有"的特性。
下面是这几个词的德语对应的英语词义:
· Eigen (德语): 对应英语中的词义"own," "proper," "characteristic," "individual"。
·Eigenwert (德语): 对应英语中的词义"own/characteristic value," 因此是 eigenvalue ( λ ) 。
·Eigenvektor (德语): 对应英语中的词义"own/characteristic vector," 因此对应 eigenvector (v).
2. 特征向量和特征值的数学意义
在线性代数中,特征向量 (eigenvector)是指在给定线性变换下方向保持不变 (或方向反转 )的非零向量,因此,特征向量是针对线性变换而言的,可以将特征向量理解为线性变换作用的"方向" 。更准确地说,线性变换 T 的特征向量 v 满足以下条件:当线性变换作用于 v 时, v 会被一个常数因子 λ 缩放,即 T ( v ) = λv 。相应的特征值、特征根或特征值是乘法因子 λ ( 可能是一个负数或复数),可以将特征值理解为线性变换作用的"程度"。
从几何角度来看,向量是具有大小和方向的多维量 (多个方向的分量之合成)。线性变换会对作用于其上的向量进行旋转、拉伸或剪切。线性变换的特征向量是指那些只被缩放(拉伸或收缩)而没有发生旋转或剪切的向量。相应的特征值是特征向量被拉伸或收缩的因子。如果特征值为负,则特征向量的方向会反转 。也就是说,向量的特征值只改变向量的大小,不改变其方向。已知一个线性变换,这个向量就确定了这个线性变换的本质,即保向性,因为称其为特征向量,而在方向不变的情况下,线性变换只是对向量进行伸缩变换,因此这个伸缩变换因子就确定了这个变换的本质,因此其为特征值。
线性变换的特征向量和特征值可以用来描述该变换的特性,因此它们在所有应用线性代数的领域都发挥着重要作用,从地质学到量子力学无所不包。特别地,在许多情况下,一个系统可以用一个线性变换来表示,该变换的输出又作为输入反馈给自身(反馈系统)。在这种应用中,最大的特征值尤为重要,因为它决定了系统在经过多次线性变换后的长期行为 ,而与之对应的特征向量则代表了系统的稳态。
一个特征向量对应一个且只有一个特征值 (因为每一个特征向量各个分量的大小是不同的),但一个特征值可以对应无穷多个特征向量 (它们彼此之间都是标量倍数关系,构成一个特征空间),或者对应几个线性无关的特征向量,具体情况取决于矩阵本身。关键在于,一个特征向量的特性与一个特定的缩放因子(即其特征值)相关联,但许多向量可以共享同一个缩放因子。
3. 线性变换简述
一个线性变换是两个向量空间之间的一个映射(函数),这个映射保留了向量加和标量乘,即,其将直线映射到直线,保持原点不变,保持平行的网格线。通常通过矩阵乘法来实现诸如旋转( rotating**)** 、缩放( scaling**)** 、剪切( shearing**)** 或反射( reflection**)** 向量等操作。它由两个核心属性定义。一个矩阵表现得像一个函数,取输入向量(坐标)并产生输出向量,有效地移动、拉伸或挤压它们所代表的空间。
3.1 从旋转来理解线性变换
旋转矩阵是一种变换矩阵。该矩阵用于在Euclid空间中对向量进行旋转。几何学提供了四种变换:旋转、反射、平移和缩放 。此外,变换矩阵利用矩阵乘法将一个向量变换到另一个向量。当我们想要改变向量的笛卡尔坐标并将其映射到新的坐标系时,我们会借助不同的变换矩阵。
在二维空间中,旋转矩阵的阶数为 2×2。类似地,n 维空间中旋转矩阵的阶数为 n ×n 。旋转矩阵描述了物体或向量在固定坐标系中的旋转。这些矩阵广泛应用于物理学、几何学和工程学的计算中。
3.1.1 2 维空间中旋转矩阵的推导
假设我们在二维空间(用笛卡尔坐标系统表示)中有一个点 ( x , y ), 则连接原点与 ( x , y )点的向量表示为 ( x , y ) ,设这个向量与 x 轴的夹角为 ν ,现在我们将这个向量按逆时针方向旋转角度 θ ,得到新的坐标 ,如下图:
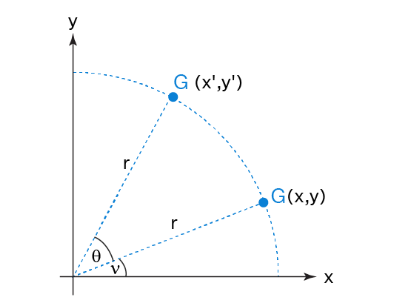
为了方便,我们设向量长度 r = 1 , 则旋转前向量的分量分别为:
x = cos(ν ) , y = sin(ν) 。
而旋转后,该点新的坐标分量分别为:
,
,
展开以上表达式,得到
,
,
代入 cos(ν ) = x , sin(ν ) = y ,消除掉含 ν的项,得到新旧坐标与旋转角之间的关系
,
,
若我们将新旧坐标之间的这种关系用矩阵和向量表示,就成了
,
即,我们将新旧坐标关系的表达式中的系数项提取出来,就构成了一个旋转矩阵,可以看出,新坐标的每一个分量的计算都需要旧坐标的所有分量参与 。
3.1.2 3 维空间中旋转矩阵的推导
在三维空间中,旋转可以绕 x 轴,y 轴或 z 轴发生。绕任一轴发生的旋转称为基本旋转或初等旋转 。下面列出了可以将向量绕任意特定轴旋转一定角度的旋转矩阵。我们假设旋转均为逆时针方向,绕 x 轴旋转的角度为 γ ,绕 y 轴旋转的角度为 β ,绕 z 轴旋转的角度为 α ,绕哪个轴旋转,这个轴的坐标就不变,因此其变换关系式中该轴上的分量不变,需只需计算另两个坐标,且其计算方法同二维的情况。
绕 x 轴沿逆时针旋转角度 γ 的旋转矩阵为
,
绕y 轴沿逆时针旋转角度 β 的旋转矩阵为
,
绕z 轴沿逆时针旋转角度 α 的旋转矩阵为
。
按照惯例,角度为正的旋转角度表示逆时针旋转。然而,如果我们根据右手定则改变符号,也可以表示顺时针旋转。右手定则指出,如果将手指弯曲成环状,指向旋转轴,则拇指指向垂直于旋转平面且与旋转轴方向一致的方向。
现在,我们求得了向量 ( x , y ,z ) 旋转后的新的坐示 ,它们之间的关系为
。
3.1.3 二维和三维旋转矩阵的属性
二维和三维旋转矩阵都具有一些共同的性质。这些属性如下:
· 旋转矩阵始终是方阵。
· 由于旋转矩阵始终是正交矩阵,因此其转置矩阵等于其逆矩阵。
· 旋转矩阵的行列式始终等于 1。
· 旋转矩阵的乘积仍然是旋转矩阵。
· 旋转矩阵两行的**叉积(外积)**等于第三行。
· 旋转矩阵一行与一列的**点积(内积)**等于 1 。
3.2 为什么用矩阵来表示线性变换
矩阵提供了一种具体的、可计算的方式来表示、构成并应用这些变换,将抽象的向量运算(例如旋转、缩放、剪切)转化为简单的矩阵向量乘法,使得这些变换易于计算、串联(矩阵乘法)甚至求逆。在本质上,矩阵是线性映射"配方"的完美存储系统,它将基向量如何缩放、旋转和平移编码化。
3.2.1 使用矩阵的关键理由
(1) 具体表示 :矩阵存储向量变换后标准基向量 (例如 (1,0) 和 (0,1))落点的坐标 ,从而提供完整的图景。
(2) 计算与算法 :矩阵乘法是应用变换的强大工具 ,它允许使用一次运算高效地完成复杂的操作(例如旋转后缩放)。
(3) 变换的组合 :连续变换(一个变换结果作为另一个变换的输入)体现在矩阵运算中只是矩阵乘法 (例如, ),这使得组合变换的计算变得简单。
(4) 可逆性 :如果一个变换可以逆转(例如旋转),则其矩阵具有逆矩阵,从而可以撤销该变换 。即逆变换只需对矩阵求逆即可。
(5) 一一对应关系:对于有限维向量空间,存在直接联系:每一个线性变换都有一个唯一的矩阵(相对于选定的基),并且每一个矩阵都定义了一个线性变换。
3.2.2 如何利用矩阵进行线性变换
(1) 一个线性变换 T 是一个函数,输入一个向量x ,输出一个向量 y 。
(2) 当使用矩阵A 表示这个变换的时候,这个运算就成为Ax = y 。
(3) 矩阵的列会告诉我们,原基向量(例如, ) 被线性变换移动到何处了。
简而言之,矩阵将抽象函数转化为有形的( tangible**)** 、可计算的形式,使线性代数成为一个实用的计算领域。
3.3 线性变换的正式定义
在线性代数中,一个线性映射(map或mapping)是向量空间之间的一种特殊函数 ,它遵循向量加 和标量乘 的基本运算。线性映射的一个标准例子是 m × n 矩阵,它将 n 维向量映射到 m 维向量,并且这种映射方式与向量加和向量之标量乘兼容。
一个线性映射是向量空间的一个同态,因此,线性映射 T :V ⟶ W 满足 T ( ax + by ) = T (ax ) + T (by )(其中,a ,b 是标量,x 和 y 是向量,即向量空间 V 的元素) 。一个线性映射总是将 V 的元素映射到 W 的元素,且 V 的线性子空间满射到 W 的线子空间。
令 V 和 W 为同一个场( field ) K ( 例如实数或复数)上的子空间。若一个函数 f :V ⟶ W 对于任意两个向量 u , v ∈V 以及任意标量 c ∈K 都满足下述两个条件,则称其为一个线性映射:
· 向量加: T ( u + v ) = T (u ) + T (v) ,
· 标量乘 :T ( cu ) = cT (u) 。
以上可推广到多维向量的情况。
3.3 线性变换与矩阵的关系
每一个有限维向量空间之间的线性变换都可以用一个矩阵来表示 。但具体的矩阵取决于所选择的输入 ( 定义域)和输出(上域)空间所选用的基。该矩阵如同一个函数,通过乘法变换向量,并提供了一种强大的方法来计算和理解这些变换,使线性代数更加具体化。
4. 线性变换与特征值的关系
对于线性变换 T : V ⟶ V ( 将一个向量空间映射到其自身),当其基于的场( field )( 例如,复数场 ℂ ) 在代数上封闭且维数有限时,其特征值总是存在。但若变项涉及复缩放( scaling )( 例如,旋转)时,则它们可能在实数场( ℝ ) 中不存在,因为特征值是特征向量用于缩放( shrink / stretch ) 的标量因子;其对于 ℂ 上的方阵都能得到保证,但对实矩阵,可能需要扩展到复数场。
也就是说,线性变换的矩阵可能有一个特征值,也可能不存在特征值,视情况而定。
4.1 特征值存在的情况
(1) 在有限维复向量空间上:复数场 ℂ 上的任意线性变换 T : V ⟶ V 都至少有一个特征值。
(2) 对称矩阵(实数场):一个实对称矩阵总是有实特征值。
(3) 常规方阵:若我们使用 n × n 矩阵( 表示 或
中的变换),则在 ℂ 中存在特征值(特征多项式之根)。
4.2 特征值不存在的情况 ( 在实数场中)
(1) 旋转: 中的一个纯旋转( 例如, T ( x , y )= ( - y , x ) ) 没有实特征值,因为没有哪个实向量仅仅是缩放的,它还会被旋转。
(2) 非代数封闭场:若代数不是代数封闭的( 如 ℝ**) ,若其特征多项式在那个场中没有根,则一个变换没有特征值。例如,** 的根为 i ,-i , 不是实根。
4.3 如何理解 ( 从几何和代数角度)
(1) 几何角度:一个特征值 λ 意味着特征向量仅乘以 λ (拉伸,收缩,剪切),变换后仍处于同一条直线上: T ( v ) = λv 。
(2) 代数角度: 线性变换写成矩阵形式的公式为 Av = λv = λIv ,都移到左边得到方程 ( A -- λI )v = 0 ;若方程 ( A -- λI )v = 0 有一个非零解 v ,则 λ 是一个特征值,意味着矩阵 ( A -- λI ) 是奇异的(不可逆),因此其行列式为零:det( A -- λI ) = 0 。原因在于: 齐性方程组的解由基本解和基本解之组合构成,因此,当我们求解特征向量时,我们实际上是在求解这个齐性方程组的非平凡解!(在这里为 v ≠ 0,如果等于零则无意义**) ,而特征值与特征向量有关。** 我们假设矩阵A -- λI 可逆,我们不妨设其逆为 ,则
。
这表明 v = 0 ,然而,我们要求 v ≠ 0。因此,若要齐性方程 ( A -- λI ) v = 0 有非平凡解,则矩阵 ( A -- λI ) 必不可逆(就有这么奇特),若矩阵不可逆,则必有其行列式等于0,即 det ( A -- λI ) = 0 。因此,求解这个多项式(称为特征多项式)方程的根,即得到矩阵的特征值,而这个变换矩阵的所有特征值就构成了这个矩阵的谱( spectrum ), 用符号 σ ( A ) 表示。
5. 如何求得矩阵的特征值(线性变换的特征值)
为了求变换(矩阵)的特征值,首先将变换表示为方阵 ( A ),然后求解特征方程 det( A -- λI ) = 0,得到标量 λ ,其中 I 为单位矩阵,λ 表示特征值,即特征向量的缩放因子 。该过程涉及求得所得多项 式方程(特征多项式) 的根,从而获得具体的特征值,从而也就求得了其特征向量。
具体步骤:
(1) 将变换表示为方阵 ( A) 。
(2) 构成矩阵 ( A -- λI) 。
(3) 计算矩阵 ( A -- λI) 的行列式。
(4) 置行列式 det( A -- λI ) = 0 ,针对变量 λ 求解方程的根。
**(5)**行列式方程构成的多项式方程的根即为变换的特征值。