🎬 胖咕噜的稞达鸭 :个人主页
🔥 个人专栏 : 《数据结构》《C++初阶高阶》
《Linux系统学习》
《算法入门》
⛺️技术的杠杆,撬动整个世界!

一维前缀和
cpp
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n, q;//n是数组元素的个数,q表示第几个
cin >> n >> q;
//1.申请一个数组
vector<int>arr(n + 1);//多申请一个元素,因为下标要从1开始
for (int i = 1; i <= n; i++)cin >> arr[i];
//2.形成一个前缀和数组
vector<long long> dp(n + 1); //long long 处理边界情况
for (int i = 1; i <= n; i++)dp[i] = dp[i - 1] + arr[i];
//3.使用前缀和数组来计算任意一段区间的和
int l = 0, r = 0;
while (q--) {
cin >> l >> r;
cout << dp[r] - dp[l - 1] << endl;//如果要计算dp[2]-dp[0];再用这个公式,算出来就是dp[2]-dp[-1],我们假定dp[0]=0;
}
return 0;
}二维数组二维前缀和
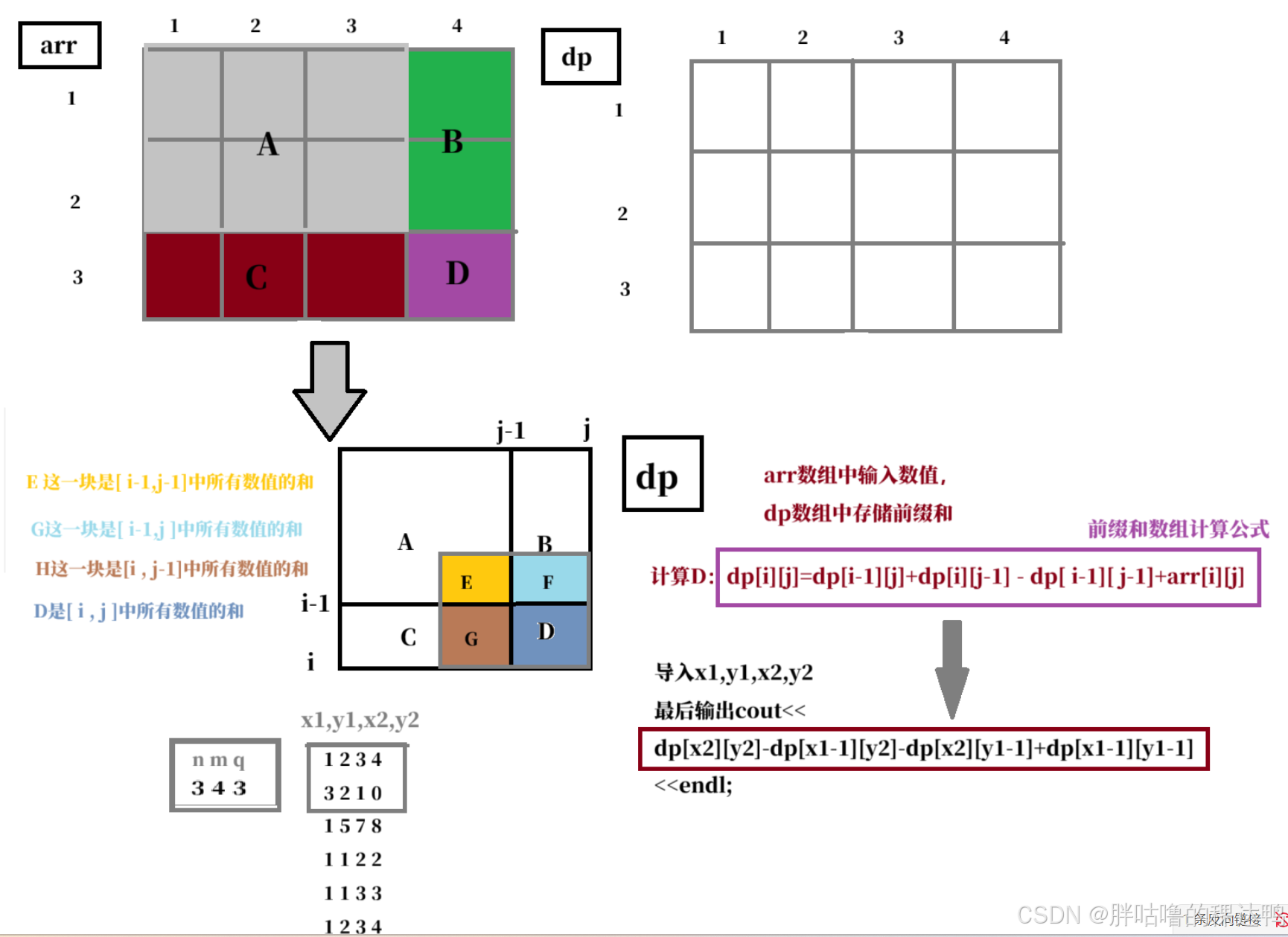
题目描述:
要求把[i,j]位置的元素计算出来,也即是二维数组,计算1到i,1到j所有下标的数值,可以类似于计算面积;看图更清楚
cpp
#include <iostream>
#include <vector>
using namespace std;
//dp[i][j]表示从【1,1】的位置到【i,j】位置,这段区间里面所有元素的和
//dp[i][j]=dp[i-1]dp[j]+dp[j-1][i]+arr[i][j]-dp[i-1][j-1]
int main() {
//1.读入数据
int n=0,m=0,q=0;
cin >> n >> m >> q;
vector<vector<int>> arr(n+1,vector<int>(m+1));
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin >> arr[i][j];
//2.预处理前缀和矩阵
vector<vector<long long>>dp(n+1,vector<long long>(m+1))
for(int i = 1;i<=n;i++)
for(int j=1;j<=m;j++)
dp[i][j]=dp[i-1][j]+dp[i][j-1]+arr[i][j]-dp[i-1][j-1];
//3.使用前缀和数组
int x1=0,x2=0,y1=0,y2=0;
while(q--)
{
cin>>x1>>y1>>x2>>y2;
cout<<dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]<<endl;
}
return 0;
}
// 64 位输出请用 printf("%lld")寻找数组的中心下标
解法:用前缀和
用f来表示前缀和数组,g来表示后缀和数组。
f[ i]表示[0,i-1]区间,所有元素的和;f [ i ]=f[i-1] + nums[i-1];
g[i]表示[i+1,n-1]区间,所有元素的和。g[i ]=g[i+1]+nums[i+1].
然后去判断是否f[i]== g[i].
处理细节:f(0)=0;g(n-1)=0;
cpp
class Solution {
public:
int pivotIndex(vector<int>& nums) {
int n =nums.size();
vector<int>f(n),g(n);
//预处理前缀和数组和后缀和数组
for(int i=1;i<n;i++)
f[i]=f[i-1]+nums[i-1];
for(int i = n-2;i>=0;i--)
g[i]=g[i+1]+nums[i+1];
//使用
for(int i =0;i<n;i++)
if(f[i] == g[i])
return i;
return -1;
}
};除自身以外数组的乘积
https://leetcode.cn/problems/product-of-array-except-self/description/
题解:返回除了这个数字之外的前面一段数组和后面一段数组的积。
解法:前缀积和后缀积
用f来表示前缀积数组,g来表示后缀积数组。
f[ i]表示[0,i-1]区间,所有元素的积;f [ i ]=f[i-1] * nums[i-1];
g[i]表示[i+1,n-1]区间,所有元素的积。g[i ]=g[i+1] * nums[i+1].
处理细节问题,如果前缀积的第一个和后缀积的最后一个为0,结果就会发生变化,所以f[0 ] = g[ n-1] =1
cpp
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
//计算nums的长度
int n = nums.size();
vector<int> f(n),g(n);
//处理细节问题,这道题涉及到乘积问题,所以前缀和的第一个数字和后缀和的最后一个数字一定是等于1,不然累积下来结果不对
f[0] = g[n-1] = 1;
for(int i = 1;i<n;i++)
f[i] = f[i-1] * nums[i-1];
for(int i = n-2;i>=0;i--)
g[i] = g[i+1] * nums[i+1];
//定义一个数组返回最后的值
vector<int>ret(n);
for(int i = 0;i< n;i++)
{
ret[i]=f[i] * g[i];
}
return ret;
}
};和为k的子数组
https://leetcode.cn/problems/subarray-sum-equals-k/description/

题解:本题涉及到数组中元素的个数及每一个元素,建议使用哈希表+前缀和的方式求解;
题目要求求解的是和为k的子数组,那么我们可以倒着加,假设最后一个元素为i,那就需要在【0,i-1】中寻找和为k的元素数组,定义一个sum ,用来统计遍历到的元素的和,
sum - k:如果存在某个之前的前缀和等于 sum - k,那么:
从那个位置到当前位置的子数组和 = sum - (sum - k) = k
举个例子:
数组: [1, 2, 3], k = 3
遍历过程:
- num=1: sum=1, sum-k=-2 → 不存在,不累加
- num=2: sum=3, sum-k=0 → hash[0]=1 → 找到1个子数组 [1,2](这一步也就解释了为什么需要hash[0]=1)
- num=3: sum=6, sum-k=3 → hash[3]=1 → 找到1个子数组 [3]
随后,更新哈希表,将当前前缀和sum在哈希表中的计数加1,如果sum不存在,hash[sum]会初始化为0然后加1。
cpp
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
unordered_map<int ,int>hash;//统计前缀和出现的次数
hash[0]=1;//hash表中0出现了一次
int sum = 0,ret = 0;
for(auto x : nums)
{
sum += x;//计算当前位置的前缀和
if(hash.count(sum - k))ret += hash[sum-k];//检查hash.count()是否存在
hash[sum]++;//将当前前缀和 sum 在哈希表中的计数加1
//如果 sum 不存在,hash[sum] 会初始化为0然后加1
}
return ret;
}
};和可被k整除的子数组
https://leetcode.cn/problems/subarray-sums-divisible-by-k/description/

同余定理:
(a-b)/p = k......0
可以说明
|
|
|
\ /
a % p = b % p 举个例子:
(26-12)/ 7 = 2
(12 % 7)= (26 % 7) = 5
其实本质也就是取余数,(12 + 2*7)/7 = 12 % 7;
也就是(a + p * k) % p = a % p;2.C++,java中【负数 % 正数】的结果以及修正
负数 % 正数 = 负数 ---> a % p + p所以在正负数中统一取模:
(a % p + p )% p前缀和+哈希表
设想有一个i,从【0,i】中有一个前缀和x,
(sum - x) % k = 0;//在[0,i]中有一段区间能够被k整除
|
|
|
\ /
sum % k = x % k;///在[0,i-1]区间内,找到有多少个前缀和的余数等于(sum % k + k) % k用一个哈希表<int,int>(前缀和的余数,次数)
cpp
class Solution {
public:
int subarraysDivByK(vector<int>& nums, int k)
{
unordered_map<int,int>hash; hash[0 % k]=1;//0这个数的余数
int sum = 0,ret = 0 ;
for(auto x : nums)
{
sum += x;
int r = (sum % k + k) % k;//修正之后的余数
if(hash.count(r))ret += hash[r];//统计结果
hash[r]++;
}
return ret;
}
};连续数组
[525. 连续数组 - 力扣(LeetCode)](https://leetcode.cn/problems/contiguous-array/description/)\]()
![!\[\[2 5.png\]\]](https://i-blog.csdnimg.cn/direct/19b31ae7e63f409c8d676cefbd091600.png)


```cpp
class Solution {
public:
int findMaxLength(vector