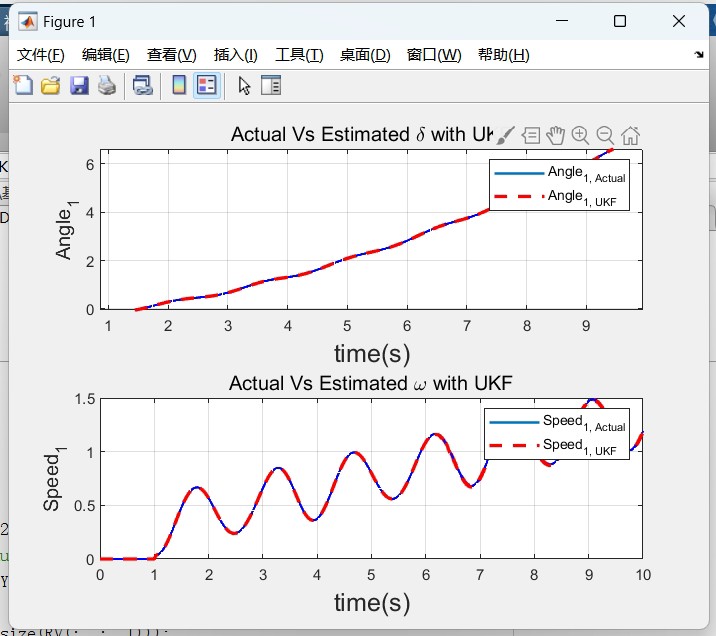
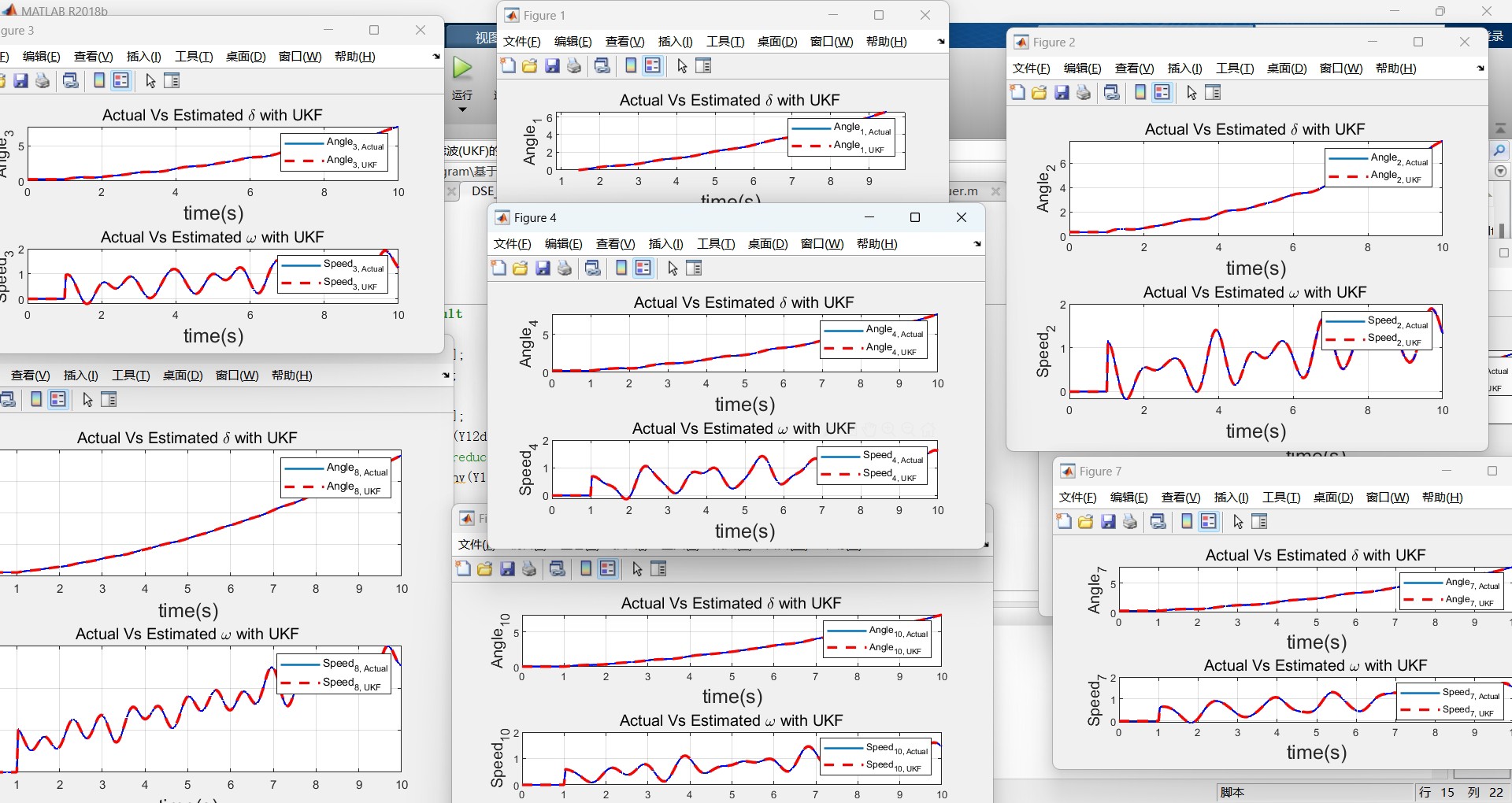
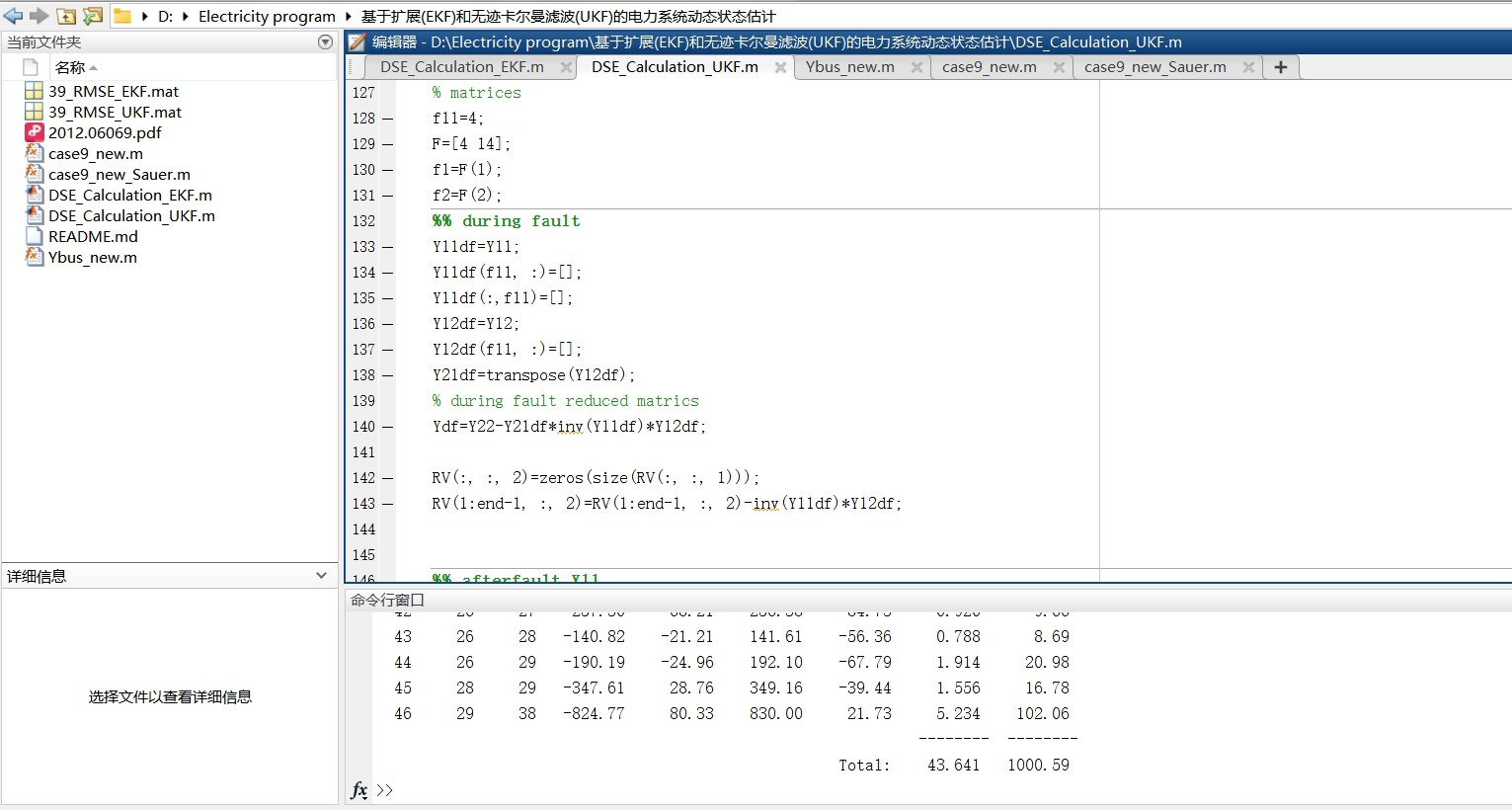
复现《基于扩展(EKF)和无迹卡尔曼滤波(UKF)的电力系统动态状态估计

复现《基于扩展(EKF)和无迹卡尔曼滤波(UKF)的电力系统动态状态估计》该程序对应文章《Power System Dynamic State Estimation Using Extended and Unscented Kalman Filters》，电力系统状态的准确估计对于提高电力系统的可靠性、弹性、安全性和稳定性具有重要意义，虽然近年来测量设备和传输技术的发展大大降低了测量和传输误差，但这些测量仍然不能完全没有测量噪声。因此，需要对噪声测量值进行过滤，从而获得准确的电力系统运行动态。本程序采用两种方法，分别是扩展卡尔曼滤波(EKF)和无迹卡尔曼滤波(UKF)，对电力系统进行动态状态估计，以39节点系统为算例验证了方法的有效性。注：该程序需要安装matpower插件，否则运行会报错。

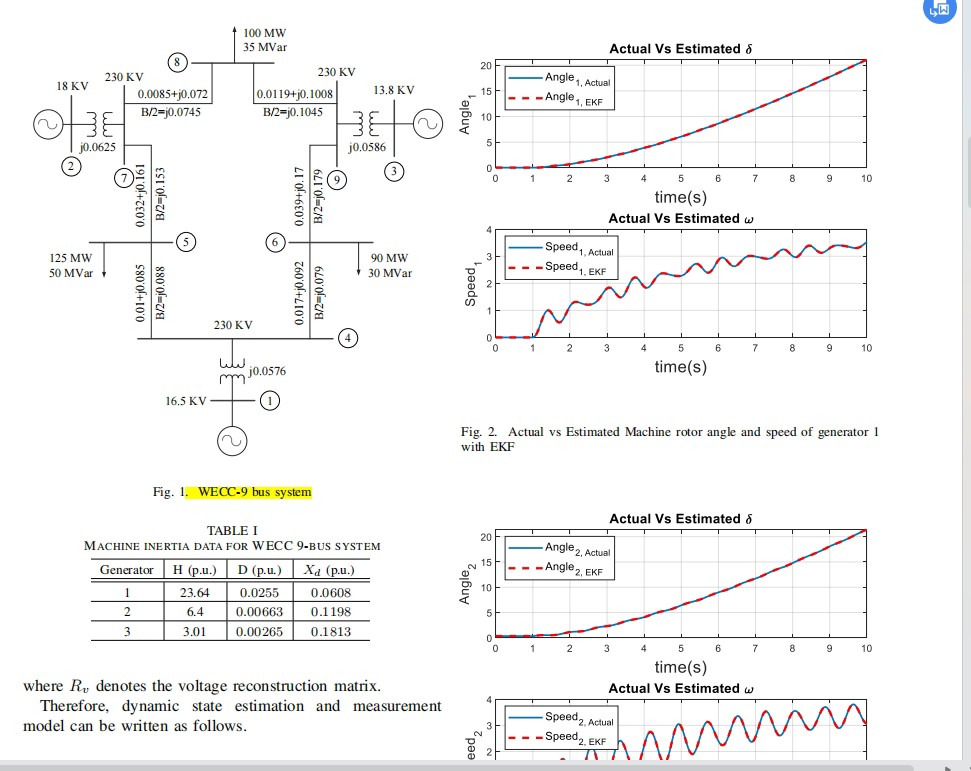
在电力系统领域，准确估计系统状态对提升其可靠性、弹性、安全性与稳定性至关重要。尽管测量设备和传输技术不断进步，测量噪声依旧无法完全消除。所以，对噪声测量值进行过滤，获取准确的电力系统运行动态成为关键，而这篇文章采用的扩展卡尔曼滤波（EKF）和无迹卡尔曼滤波（UKF）方法就为我们提供了有效的解决思路，今天就来尝试复现相关程序。

前置条件：安装matpower插件

值得注意的是，该程序运行依赖matpower插件，如果没有安装，运行时将会报错。具体的安装过程可参考matpower官方文档，按照对应系统和Matlab版本进行正确安装。

扩展卡尔曼滤波（EKF）

EKF原理简述

EKF是一种用于非线性系统状态估计的方法，它通过对非线性系统进行一阶泰勒展开线性化，从而应用卡尔曼滤波框架进行状态估计。

代码实现示例（Matlab）

matlab 复制代码

% 假设已经有了系统模型函数f(x, u)和观测函数h(x)
% 初始化参数
x_hat = zeros(n, 1); % 初始状态估计
P = eye(n); % 初始估计协方差
Q = Q_matrix; % 过程噪声协方差
R = R_matrix; % 观测噪声协方差

for k = 1:num_steps
    % 预测步骤
    x_hat_minus = f(x_hat, u(:, k));
    F = jacobian(f(x_hat, u(:, k)), x_hat);
    P_minus = F * P * F' + Q;
    
    % 更新步骤
    y = h(x_hat_minus);
    H = jacobian(h(x_hat_minus), x_hat_minus);
    K = P_minus * H' / (H * P_minus * H' + R);
    x_hat = x_hat_minus + K * (z(:, k) - y);
    P = (eye(n) - K * H) * P_minus;
end

代码分析

初始化部分 ：首先初始化状态估计 x_hat 为零向量，估计协方差 P 为单位矩阵，同时设定过程噪声协方差 Q 和观测噪声协方差 R。这些初始值的设定对后续估计结果有一定影响，需要根据实际系统特性进行调整。
预测步骤 ：通过系统模型函数 f(x, u) 预测下一时刻状态 xhatminus。然后计算系统的雅克比矩阵 F，用于近似非线性系统的线性化，进而更新预测协方差 P_minus。
更新步骤 ：利用观测函数 h(x) 计算预测观测值 y，并计算观测雅克比矩阵 H。通过卡尔曼增益 K 的计算，结合实际观测值 z 对预测状态进行更新，同时更新估计协方差 P。

无迹卡尔曼滤波（UKF）

UKF原理简述

UKF则是采用确定性采样策略，通过一组Sigma点来近似非线性系统的概率分布，相较于EKF，它在处理高度非线性系统时可能具有更好的性能。

代码实现示例（Matlab）

matlab 复制代码

% 假设已经有了系统模型函数f(x, u)和观测函数h(x)
% 初始化参数
x_hat = zeros(n, 1); % 初始状态估计
P = eye(n); % 初始估计协方差
Q = Q_matrix; % 过程噪声协方差
R = R_matrix; % 观测噪声协方差
lambda = alpha^2 * (n + kappa) - n; % UKF参数计算
Wm = [lambda / (n + lambda), 0.5 / (n + lambda) * ones(1, 2 * n)]; % 均值权重
Wc = [lambda / (n + lambda) + (1 - alpha^2 + beta), 0.5 / (n + lambda) * ones(1, 2 * n)]; % 协方差权重

for k = 1:num_steps
    % 产生Sigma点
    X = [x_hat, x_hat + chol((n + lambda) * P)', x_hat - chol((n + lambda) * P)'];
    
    % 预测步骤
    X_minus = zeros(n, 2 * n + 1);
    for i = 1:2 * n + 1
        X_minus(:, i) = f(X(:, i), u(:, k));
    end
    x_hat_minus = Wm * X_minus;
    P_minus = zeros(n, n);
    for i = 1:2 * n + 1
        P_minus = P_minus + Wc(i) * (X_minus(:, i) - x_hat_minus) * (X_minus(:, i) - x_hat_minus)';
    end
    P_minus = P_minus + Q;
    
    % 更新步骤
    Y = zeros(m, 2 * n + 1);
    for i = 1:2 * n + 1
        Y(:, i) = h(X_minus(:, i));
    end
    y_hat = Wm * Y;
    P_yy = zeros(m, m);
    P_xy = zeros(n, m);
    for i = 1:2 * n + 1
        P_yy = P_yy + Wc(i) * (Y(:, i) - y_hat) * (Y(:, i) - y_hat)';
        P_xy = P_xy + Wc(i) * (X_minus(:, i) - x_hat_minus) * (Y(:, i) - y_hat)';
    end
    P_yy = P_yy + R;
    K = P_xy / P_yy;
    x_hat = x_hat_minus + K * (z(:, k) - y_hat);
    P = P_minus - K * P_yy * K';
end

代码分析

初始化部分 ：同样先初始化状态估计、估计协方差、噪声协方差等。这里还计算了UKF特有的参数 lambda，以及均值权重 Wm 和协方差权重 Wc，这些参数决定了Sigma点的分布和权重分配。
产生Sigma点 ：根据当前状态估计和协方差，通过Cholesky分解产生一组Sigma点 X，这些点能够更好地近似非线性系统的概率分布。
预测步骤 ：将Sigma点通过系统模型函数 f(x, u) 得到预测的Sigma点 Xminus*，进而计算预测状态 x* hatminus**和预测协方差 P minus，并考虑过程噪声 Q。
更新步骤 ：将预测的Sigma点通过观测函数 h(x) 得到预测观测值 Y，计算预测观测均值 yhat*，以及交叉协方差 P* xy 和观测协方差 P_yy。通过卡尔曼增益 K 的计算，结合实际观测值 z 对预测状态进行更新，同时更新估计协方差 P。

通过以39节点系统为算例，利用上述EKF和UKF方法进行动态状态估计，验证了这两种方法在电力系统状态估计中的有效性。这不仅有助于我们更好地理解电力系统的运行动态，也为实际工程应用提供了理论和方法支持。希望大家在复现过程中能进一步探索和优化这些算法，为电力系统的发展贡献自己的力量。