DASCTF 2025下半年|矩阵博弈,零度突围 Crypto -- Serration详解
Serration
题目描述:
cmd
They say Montgomery is resistant to SCA, so please drop me Montgomery form messages and help me find out the speed-determining steps to optimize my project!main.py
python
from Crypto.Util.number import *
from hashlib import sha256
import socketserver
import signal
import os
import string
import random
from sympy.ntheory.modular import crt
from line_profiler import LineProfiler
flag = b'flag{Hello_this_is_local_test}' # os.getenv('DASFLAG')
def euclide_ext(a, b):
x, xx, y, yy = 1, 0, 0, 1
while b:
q = a // b
a, b = b, a % b
x, xx = xx, x - xx * q
y, yy = yy, y - yy * q
return x, y, a
class Montgomery:
n: int
k: int
r: int
r_inv: int
n_inv: int
def __init__(self, n, k):
"""预计算n'"""
self.n = n
self.k = k
self.r = 2 ** k
self.r_inv, self.n_inv, gcd = euclide_ext(self.r, self.n)
self.n_inv = -self.n_inv # 满足 r · r_inv - n · n' = 1
if gcd != 1:
raise ValueError("gcd(r,n) must be 1")
if self.r * self.r_inv - self.n * self.n_inv != 1:
raise ValueError(
f"For ({self.r} that created from {2} ** {k},{n}) doesn't exists diophantine equation decision"
)
self.r_inv = self.r_inv % self.n
def mon_pro(self, a_n, b_n):
"""蒙哥马利乘法"""
# T = \bar{a} * \bar{b}
t = a_n * b_n
# m = T · n'(mod r) <-- (t * self.n_inv % self.r)
# u = (T + m · n) / r <-- r = 2 ** k
u = (t + (t * self.n_inv % self.r) * self.n) >> self.k
if u > self.n:
u -= self.n
return u
def mon_exp(self, a: int, e: int):
"""蒙哥马利模幂"""
# \bar{a} = a · r (mod n)
a = a * self.r % self.n
# x 初始化位 r (mod n)
x = self.r % self.n
for i in reversed(range(0, e.bit_length())):
"""快速幂算法扫描(存在侧信道计时攻击)<-->《碰碰碰,撞撞撞》侧信道攻击???"""
x = self.mon_pro(x, x)
if (e & (1 << i)) :
x= self.mon_pro(x, a)
return self.mon_pro(x, 1)
class Task(socketserver.BaseRequestHandler):
def _recvall(self):
BUFF_SIZE = 2048
data = b''
while True:
part = self.request.recv(BUFF_SIZE)
data += part
if len(part) < BUFF_SIZE:
break
return data.strip()
def send(self, msg, newline=True):
try:
if newline:
msg += b'\n'
self.request.sendall(msg)
except:
pass
def recv(self, prompt=b'> '):
self.send(prompt, newline=False)
return self._recvall()
def handle(self):
bits=1024
p=getPrime(bits)
q=getPrime(bits)
e=getPrime(bits-10)
n=p*q
print(p,",",q)
print(flag)
print(f"p = {p}")
print(f"q = {q}")
print(f"n = {n}")
# P --> 蒙哥马利域上
P=Montgomery(p,bits)
# Q --> 蒙哥马利域上
Q=Montgomery(q,bits)
# 已知(n, e)
self.send(str((n,e)).encode())
# signal.alarm(300)
for i in range(800):
lp = LineProfiler()
lp.add_function(Q.mon_pro)
lp_exp = lp(P.mon_exp)
lq_exp = lp(Q.mon_exp)
self.send(b"leave message 4 me",newline=False)
m=int(self.recv())
cp=lp_exp(m,e)
cq=lq_exp(m,e)
c=crt([p,q],[cp,cq])
d={}
for i in lp.code_map:
for j in lp.code_map[i]:
d[j]=(lp.code_map[i][j]['total_time'], lp.code_map[i][j]['nhits'])
self.send(str(d).encode())
self.send(b"can you break me?",newline=False)
guess=int(self.recv())
if guess in {p,q}:
self.send(flag.encode())
else:
self.send(b"sorry~")
exit
class ThreadedServer(socketserver.ThreadingMixIn, socketserver.TCPServer):
pass
class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
pass
if __name__ == "__main__":
HOST, PORT = '127.0.0.1', 9999
print("HOST:POST " + HOST+":" + str(PORT))
server = ForkedServer((HOST, PORT), Task)
server.allow_reuse_address = True
server.serve_forever()Analysis
-
根据题目描述我们可以获悉这道题目考察的为RSA(蒙哥马利模幂)的侧信道攻击。
-
首先,针对于RSA 而言,侧信道发生在平方-乘 处是比较常见的,但是分析代码,我们能够获得的侧信道数据并不是在平方-乘 这里,后面仔细想想,侧信道如果发生在这里,应该是在解密阶段,直接通过侧信道攻击获取解密指数d ,在这里,题目会指数e ,两者都在指明,侧信道攻击并不发生在平方-乘这里。
-
此后,我们看针对于RSA 而言,我们能够获得的关键信息是什么?连接靶机后,进行调试,我们可以选择加密的明文m,此后可以得到模乘的次数以及
pythonif u > self.n: u -= self.n发生的次数,这里大概率是论文题目了,非常用侧信道攻击一般人不是一时半会儿能实验验证的。A Timing Attack against RSA with the Chinese Remainder Theorem在解析这篇论文之前,先复习一下课程内学习的蒙哥马利模幂运算究竟是如何进行的(由于课程实验作业的原因,这里先对蒙哥马利的原理以及基础实现先留个坑)先写下蒙哥马利模幂执行的伪代码,后面有时间再进行补充。
- z : = a ′ b ′ 2. r : = ( z ( m o d R ) ) m ∗ ( m o d R ) 3. s : = ( z + r m ) / R 4. if s ≥ m then s : = s − m 5. return s \begin{aligned} &1.\quad z := a' b' \\ &2.\quad r := (z \pmod{R}) m^* \pmod{R} \\ &3.\quad s := (z + rm) / R \\ &4.\quad \text{if } s \ge m \text{ then } s := s - m \\ &5.\quad \text{return } s& \end{aligned} 1.z:=a′b′2.r:=(z(modR))m∗(modR)3.s:=(z+rm)/R4.if s≥m then s:=s−m5.return s
-
接下来就是分析这篇论文了:

这里讲一下论文的关键部分,那就是蒙哥马利在实现的过程中,涉及到一个便于计算机完成除法 操作的域,该域与我们常规计算的整数域是同构的,我们将需要将我们需要进行模幂运算的数据转化为蒙哥马利域 中,在该域中进行计算,在蒙哥马利域 上完成模幂运算后在逆映射回整数域上,由此我们完成了模幂运算的一个加速效果,而该论文则是对于采用蒙哥马利运算,中国剩余定理辅助完成模幂运算的RSA,通过适应性选择明文攻击完成对模数N进行分解的攻击
论文发现,对于上面我们提到的蒙哥马利的执行流程中,存在:
步骤3计算出的 s s s 实际上是 a ′ b ′ R − 1 ( m o d m ) a'b'R^{-1} \pmod m a′b′R−1(modm) 的一个代表元,但它可能并未完全约减到 [ 0 , m − 1 ] [0, m-1] [0,m−1] 区间,而是落在 [ 0 , 2 m − 1 ] [0, 2m-1] [0,2m−1] 区间内。步骤4的条件减法(Extra Reduction)用于将其归一化。
-
如果 s < m s < m s<m,步骤4不执行,仅包含基本的乘法和位移操作。
-
如果 s ≥ m s \ge m s≥m,步骤4执行,产生额外的减法操作。
在硬件或软件实现中,这种条件分支会导致执行时间的差异。尽管单次差异极小(可能仅几个时钟周期),但在一次模幂运算中会进行成百上千次蒙哥马利乘法,这些微小的差异会叠加 。
-
-
这完全符合我们遇到的这道2025DASCTF 的这道赛题,不过是,原论文中是针对于解密过程发生的攻击策略,但是这道题目是针对于加密过程进行的,但是RSA 的加密与解密过程都涉及到模幂 运算,因此攻击时完全适用的,但是在这里需要注意的就是,一般情况下,解密时的私钥参数d 是很大的,这也是论文可以完成攻击的一个前提,正如上面所说在硬件或软件实现中,这种条件分支会导致执行时间的差异。尽管单次差异极小(可能仅几个时钟周期),但在一次模幂运算中会进行成百上千次蒙哥马利乘法,这些微小的差异会叠加 。这也是为何出题人会对加密指数e采用如此大数的原因。
-
对于论文中提到的相关内容,我们可以连接上靶机进行简单的输入尝试:
python# q.bit_length() = 1024 q = 170359112421709529452284198507203565795845987977151535793657862209010553480001372002306100837287226849203409554246553108061021877954233011552749968739407151690783744431499104730376382582847220297130683081244692948484863921167059475129354785479793248971761145259155430813597935999325436979040203326957036239241 R = 2 ** 1024 a_list = [19, 37, 55, 73, 91, 109, 127, 145, 163, 182, 200, 218] max_diff = 163 * R % q diff = 975493260312425680650428216623229608715209469727349157757921132012351621008731655063324105121661754702731692999428615301199842470928014630995654538201643325069062550904254903711316251667491495327485406119062182125702220009798160927304934381181461523152567601399817139310357094548409114727449278947654075691 # Why??? # 163为何特殊? # 为何形成一个周期为18的diff相同? # 猜测:蒙哥马利域上的特殊点。这里简单解释一下我当时测试的一个场景,那就是我发现对于q 发生步骤4(最终减法)的次数会呈现出周期,这里说的周期是,例如在m=19 时,步骤4 发生的次数为250次 左右,此后19~37 的过程中,步骤4 发生的次数会逐渐增大,但是当m=37 时,就会突然降到250次 左右,这里体现出的周期性就是论文攻击的原理,详细解释一下就是:
在进行蒙哥马利模幂计算前,我们需要先把整数域上的数字转化到蒙哥马利域上去,计算公式就是 a ′ = a ⋅ R ( m o d p ) , 其中 R 一般取 2 p . b i t _ l e n g t h ( ) ,为何会呈现出周期性呢?而且发生周期的参数 m 都会有一个特点,那就是形成了一个等差数列 设周期参数 m 有 m 0 , m 1 , m 2 ,其中 m 2 − m 1 ≡ m 1 − m 0 ( m o d q ) ,这变相地反映了一件事就是,设 t e m p ≡ R ( m o d p ) 设周期为 T ,则有 ( T − 1 ) ⋅ t e m p < p 且 T ⋅ t e m p > p (或 T ⋅ t e m p < p 且 ( T + 1 ) ⋅ t e m p > p ) \begin{aligned} &在进行蒙哥马利模幂计算前,我们需要先把整数域上的数字转化到蒙哥马利域上去,计算公式就是a'=a\cdot R(mod\ p),\\ &其中R一般取2^{p.bit\_length()},为何会呈现出周期性呢?而且发生周期的参数m都会有 一个特点,那就是形成了一个等差数列\\ &设周期参数m有m_0,m_1,m_2,其中m_2-m_1\equiv m_1-m_0\ (mod\ q),这变相地反映了一件事就是,设temp \equiv R\ (mod\ p)\\ &设周期为T,则有(T - 1)\cdot temp < p 且T\cdot temp > p(或T\cdot temp < p 且(T + 1)\cdot temp > p)& \end{aligned} 在进行蒙哥马利模幂计算前,我们需要先把整数域上的数字转化到蒙哥马利域上去,计算公式就是a′=a⋅R(mod p),其中R一般取2p.bit_length(),为何会呈现出周期性呢?而且发生周期的参数m都会有一个特点,那就是形成了一个等差数列设周期参数m有m0,m1,m2,其中m2−m1≡m1−m0 (mod q),这变相地反映了一件事就是,设temp≡R (mod p)设周期为T,则有(T−1)⋅temp<p且T⋅temp>p(或T⋅temp<p且(T+1)⋅temp>p) -
上述我们进行地一个选择明文是直接进行递增遍历的,但是真实攻击肯定不能如此,因为我们虽然在不断缩小p 的范围,但是题目只给了我们600 次交互机会以及必须限时5min ,我们需要完全复现论文中的攻击方法,论文指出:
引理 1 译文 1 : ( i ) 蒙哥马利算法需要额外约减步骤当且仅当: a ′ b ′ R m + a ′ b ′ m ∗ ( m o d R ) R ≥ 1 ( i i ) 设随机变量 B 在 Z m 上均匀分布。除非比率 R / gcd ( R , Ψ ( a ) ) 极小,否则对于 a ∈ Z m : Prob ( extra reduction in Ψ ∗ ( Ψ ( a ) B ) ) = Ψ ( a ) 2 R ... ( 2 ) 同样地: Prob ( extra reduction in Ψ ∗ ( B 2 ) ) = m 3 R ... ( 3 ) \begin{aligned} &引理 1 译文 1:\\ &(i) 蒙哥马利算法需要额外约减步骤当且仅当:\\ &\frac{a' b'}{Rm} + \frac{a' b' m^* \pmod R}{R} \ge 1\\ &(ii) 设随机变量 B 在 \mathbb{Z}m 上均匀分布。除非比率 R/\gcd(R, \Psi(a)) 极小,否则对于 a \in \mathbb{Z}m:\\ & \text{Prob}(\text{extra reduction in } \Psi*(\Psi(a)B)) = \frac{\Psi(a)}{2R} \quad \dots(2)\\ 同样地:\\ &\text{Prob}(\text{extra reduction in } \Psi*(B^2)) = \frac{m}{3R} \quad \dots(3)& \end{aligned} 同样地:引理1译文1:(i)蒙哥马利算法需要额外约减步骤当且仅当:Rma′b′+Ra′b′m∗(modR)≥1(ii)设随机变量B在Zm上均匀分布。除非比率R/gcd(R,Ψ(a))极小,否则对于a∈Zm:Prob(extra reduction in Ψ∗(Ψ(a)B))=2RΨ(a)...(2)Prob(extra reduction in Ψ∗(B2))=3Rm...(3) -
这就是我们攻击完成的理论依据,但是我对其进行如下总结:
想象我们在整数轴上连续增加输入值 u u u。
- 当 u u u 在两个 p i p_i pi 的倍数之间(例如 k p i < u < ( k + 1 ) p i k p_i < u < (k+1) p_i kpi<u<(k+1)pi)逐渐增加时, u ( m o d p i ) u \pmod{p_i} u(modpi) 也随之线性增加。
根据公式(7),额外约减的概率线性上升,导致平均执行时间缓慢增加。 - 关键时刻发生在 u u u 跨越 p i p_i pi 的倍数时。当 u u u 从 k p i − ϵ k p_i - \epsilon kpi−ϵ 变为 k p i + ϵ k p_i + \epsilon kpi+ϵ 时, u ( m o d p i ) u \pmod{p_i} u(modpi) 从一个接近 p i p_i pi 的最大值瞬间跌落至接近 0 0 0 的最小值。
- 物理效应:这一数学上的"跌落"会导致额外约减的概率发生剧烈的阶跃式下降。反映在侧信道上,就是总执行时间的突然减少。
- 攻击策略:攻击者只需寻找这个时间上的"断崖",就能精确定位 k p i k p_i kpi 的位置。由于攻击者已知 n n n,只要找到 p 1 p_1 p1 或 p 2 p_2 p2 的任何倍数,通过计算 gcd ( u , n ) \gcd(u, n) gcd(u,n) 即可分解 n n n。(这个过程是需要我们不断地进行二分逼近精确定位 k p i k p_i kpi,具体可见Demo代码部分。)
在原文的总结中,时间体现在总执行时间 的突然减少,但是为了赛题的可解性以及不必要的噪声,我们这道题目变得更加简单,我们只需要统计发生最终减法的次数就可以了,下面是我做的一个论文的攻击实验复现:
- 当 u u u 在两个 p i p_i pi 的倍数之间(例如 k p i < u < ( k + 1 ) p i k p_i < u < (k+1) p_i kpi<u<(k+1)pi)逐渐增加时, u ( m o d p i ) u \pmod{p_i} u(modpi) 也随之线性增加。
Demo
python
# sage 10.7
from sympy.ntheory.modular import crt
from Crypto.Util.number import getPrime, GCD, inverse
def euclide_ext(a, b):
x, xx, y, yy = 1, 0, 0, 1
while b:
q = a // b
a, b = b, a % b
x, xx = xx, x - xx * q
y, yy = yy, y - yy * q
return x, y, a
class Montgomery:
def __init__(self, n, k):
self.n = n
self.k = k
self.r = 1 << k
self.r_inv, self.n_inv, gcd = euclide_ext(self.r, self.n)
self.n_inv = -self.n_inv
mask = (1 << k) - 1
self.n_inv = self.n_inv & mask
self.r_inv = self.r_inv % self.n
def mon_pro(self, a_n, b_n):
"""蒙哥马利乘法"""
# T = \bar{a} * \bar{b}
t = a_n * b_n
# m = T · n'(mod r) <-- (t * self.n_inv % self.r)
# u = (T + m · n) / r <-- r = 2 ** k
u = (t + (t * self.n_inv % self.r) * self.n) >> self.k
if u > self.n:
u -= self.n
self.counter += 1
return u
def mon_exp(self, a: int, e: int):
# 清零,只计算当前的counter
self.counter = 0
"""蒙哥马利模幂"""
# \bar{a} = a · r (mod n)
a = a * self.r % self.n
# x 初始化位 r (mod n)
x = self.r % self.n
for i in reversed(range(0, e.bit_length())):
"""NO:快速幂算法扫描(存在侧信道计时攻击)<-->《碰碰碰,撞撞撞》侧信道攻击???"""
x = self.mon_pro(x, x)
if (e & (1 << i)) :
x= self.mon_pro(x, a)
# print(f"counter = {self.counter}")
return self.mon_pro(x, 1)
def attack_oracle_sampled(u_start, n, R_inv_n, e, P_ctx, Q_ctx, window_size = 6):
total_cost = 0
for offset in range(0, window_size * 2, 2):
u_target = u_start + offset
m = (u_target * R_inv_n) % n
P_ctx.mon_exp(m % P_ctx.n, e)
Q_ctx.mon_exp(m % Q_ctx.n, e)
total_cost += (P_ctx.counter + Q_ctx.counter)
return total_cost
def attack():
bits = 1024
p = getPrime(bits)
q = getPrime(bits)
e = getPrime(bits - 10)
n = p * q
print(f"p = {p}")
print(f"n = {n}")
print(f"e = {e}")
P = Montgomery(p, bits)
Q = Montgomery(q, bits)
R = 1 << bits
R_inv_n = inverse(R, n)
print("Beginning attack...")
delta = R // 100
u_curr = R - delta
SAMPLE_SIZE = 6
t_curr = attack_oracle_sampled(u_curr, n, R_inv_n, e, P, Q, SAMPLE_SIZE)
found_interval = None
threshold = -30 * SAMPLE_SIZE
for step in range(100):
u_next = u_curr - delta
if u_next < 0: break
t_next = attack_oracle_sampled(u_next, n, R_inv_n, e, P, Q, SAMPLE_SIZE)
diff = t_curr - t_next
if diff < threshold:
found_interval = (u_next, u_curr)
break
u_curr = u_next
t_curr = t_next
low, high = found_interval
# Low Bound = High Reduction Count (Time Max)
# High Bound = Low Reduction Count (Time Min)
time_left_baseline = attack_oracle_sampled(low, n, R_inv_n, e, P, Q, SAMPLE_SIZE)
time_right_baseline = attack_oracle_sampled(high, n, R_inv_n, e, P, Q, SAMPLE_SIZE)
print(f"Baseline Left (High Cost): {time_left_baseline}")
print(f"Baseline Right (Low Cost): {time_right_baseline}")
while (high - low) > 500:
mid = (low + high) // 2
t_mid = attack_oracle_sampled(mid, n, R_inv_n, e, P, Q, SAMPLE_SIZE)
dist_to_left = abs(t_mid - time_left_baseline)
dist_to_right = abs(t_mid - time_right_baseline)
if dist_to_left < dist_to_right:
# 说明 mid 的表现更像左边(高约简),说明 mid < p
# p 在 mid 右边
low = mid
time_left_baseline = t_mid
else:
# 说明 mid 的表现更像右边(低约简),说明 mid > p
# p 在 mid 左边
high = mid
time_right_baseline = t_mid
print(f"Interval narrowed to size {high - low}")
P.<x> = PolynomialRing(Zmod(n))
f = x + low
roots = f.small_roots(X=2**480, beta=0.5, epsilon=0.03)
if roots:
root = int(roots[0])
p = low + root
if p > 1 and n % p == 0:
print(f"Successfully search p: {p}")
return
if __name__ == "__main__":
attack()
- 这里就是按照查找n 与我们找到的kp 的公因数来进行分解的n ,但是论文中还提及到的一种方法就是,可以利用Coppersmith 进行小根求解,进一步增大攻击的力度,而这道题目就是后者的这种攻击情况,而并不意味着我们完成的Demo 就失效了,取公因数的方法就在于你有足够多的适应性选择明文攻击 的机会,能够准确找到kp 才能完成攻击,但是题目中给出的600 次交互次数使得我们没法准确地通过二分搜索找到准确的kp ,也没法将其限制到一个小范围中(如果我们知道**[p - 1000, p + 1000]**是可以进行爆破的,1000只是代表一个小范围),论文中也给出了一个大致的参数数据:
| 模数长度 (n) | R 参数 | 优化步长参数 (s) | 平均所需测量次数 | 单次决策错误率 (perr) |
|---|---|---|---|---|
| 512 bit | 2 256 2^{256} 2256 | 11 | 0.71 log 2 n 0.71 \log_2 n 0.71log2n | - |
| 1024 bit | 2 512 2^{512} 2512 | 46 | 560 ( ≈ 0.55 log 2 n ) 560 (\approx 0.55 \log_2 n) 560(≈0.55log2n) | 0.00094 |
| 2048 bit | 2 1024 2^{1024} 21024 | 625 | 0.51 log 2 n 0.51 \log_2 n 0.51log2n | 0.000005 |
之后我们就可以开始写交互脚本完成赛题的求解了,这里由于后续也懒得改一个完全自动化的脚本来获取flag 了,在完成攻击后,我们可能需要手动消耗一下600 次剩余的交互次数,进而进入挑战环节,输入p或q 进行应答获取flag即可。
Exp
python
from pwn import *
from sympy.ntheory.modular import crt
from Crypto.Util.number import inverse, GCD
from tqdm import tqdm
def euclide_ext(a, b):
x, xx, y, yy = 1, 0, 0, 1
while b:
q = a // b
a, b = b, a % b
x, xx = xx, x - xx * q
y, yy = yy, y - yy * q
return x, y, a
class Montgomery:
def __init__(self, n, k):
self.n = n
self.k = k
self.r = 1 << k
self.r_inv, self.n_inv, gcd = euclide_ext(self.r, self.n)
self.n_inv = -self.n_inv
mask = (1 << k) - 1
self.n_inv = self.n_inv & mask
self.r_inv = self.r_inv % self.n
def mon_pro(self, a_n, b_n):
t = a_n * b_n
u = (t + (t * self.n_inv % self.r) * self.n) >> self.k
if u > self.n:
u -= self.n
self.counter += 1
return u
def mon_exp(self, a: int, e: int):
self.counter = 0
a = a * self.r % self.n
x = self.r % self.n
for i in reversed(range(0, e.bit_length())):
x = self.mon_pro(x, x)
if (e & (1 << i)):
x = self.mon_pro(x, a)
return self.mon_pro(x, 1)
def get_data(response):
response = eval(response)
# 48:nhits
if 48 in response:
total_time, nhits = response[48]
return nhits
def attack(io, n, e, R_inv_n, u_start, window_size=6):
total_cost = 0
for i in range(0, window_size * 2, 2):
u_target = u_start + i
m = (u_target * R_inv_n) % n
io.sendlineafter(b"> ", str(m).encode())
response = io.recvline().strip().decode()
if response.startswith("{"):
counter = get_data(response)
total_cost += counter
else:
print(f"Unexpected response: {response}")
return total_cost
def search(io, n, e, R_inv_n, low, high, times, sample_size=1):
print(f"Getting baseline costs...")
time_left_baseline = attack(io, n, e, R_inv_n, low, sample_size)
time_right_baseline = attack(io, n, e, R_inv_n, high, sample_size)
print(f"Baseline Left (High Cost): {time_left_baseline}")
print(f"Baseline Right (Low Cost): {time_right_baseline}")
# 二分
for i in tqdm(range(times)):
if high - low <= 500:
break
mid = (low + high) // 2
# print(f"Search iteration {i+1}: mid={mid}, interval=[{low}, {high}], size={high-low}")
t_mid = attack(io, n, e, R_inv_n, mid, sample_size)
# 距离判决
dist_to_left = abs(t_mid - time_left_baseline)
dist_to_right = abs(t_mid - time_right_baseline)
if dist_to_left < dist_to_right:
# mid < p
low = mid
time_left_baseline = t_mid
# print(f"Left -> {mid}")
else:
# mid > p
high = mid
time_right_baseline = t_mid
# print(f"Right -> {mid}")
return low, high
def factor_n(n, low, high):
"""尝试分解n"""
print(f"Attempting to factor n with interval [{low}, {high}]")
R.<x> = PolynomialRing(Zmod(n))
f = x + low
roots = f.small_roots(X=2**490, beta=0.5, epsilon=0.02)
if roots:
root = int(roots[0])
p_guess = low + root
if p_guess > 1 and n % p_guess == 0:
print(f"[+] Found factor with Coppersmith: {p_guess}")
return p_guess
return None
def main():
io = remote("127.0.0.1", 9999)
# (n, e)
response = io.recvline().strip().decode()
print(f"Received from server: {response}")
if response.startswith("("):
n_str, e_str = response[1:-1].split(",")
n = int(n_str.strip())
e = int(e_str.strip())
print(f"n = {n}")
print(f"e = {e}")
bits = 1024
R = 1 << bits
R_inv_n = inverse(R, n)
print(f"Beginning attack...")
delta = R // 100
u_curr = R - delta
SAMPLE_SIZE = 2
found_interval = None
# 初始成本
print(f"Initial scanning...")
t_curr = attack(io, n, e, R_inv_n, u_curr, SAMPLE_SIZE)
# 边界
threshold = -30 * SAMPLE_SIZE
for step in range(100):
u_next = u_curr - delta
if u_next < 0:
break
# print(f"Step {step+1}: u={u_curr} -> {u_next}")
t_next = attack(io, n, e, R_inv_n, u_next, 1)
diff = t_curr - t_next
if diff < threshold:
found_interval = (u_next, u_curr)
print(f"Found: [{u_next}, {u_curr}]")
break
u_curr = u_next
t_curr = t_next
low, high = found_interval
print(f"Search...")
low, high = search(io, n, e, R_inv_n, low, high, 565) # 待解决:times计算
print(f"Final range: [{low}, {high}], size={high-low}")
factor = factor_n(n, low, high)
if factor is not None:
print(f"p = {factor}")
io.interactive()
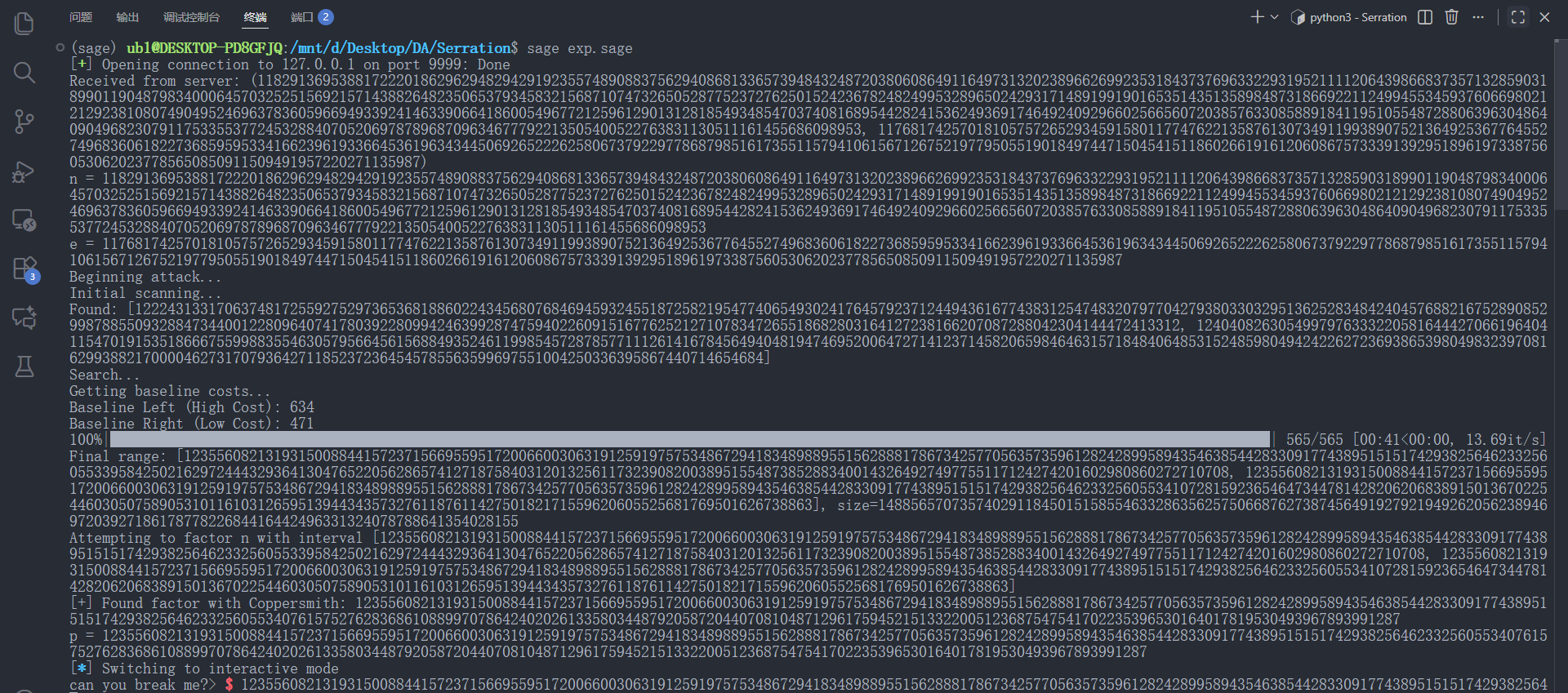
if __name__ == "__main__":
main()