目录
[【202. 快乐数】](#【202. 快乐数】)
[【11. 盛水最多容器】](#【11. 盛水最多容器】)
引言:
常见的双指针有两种形式,一种是对撞指针,一种是快慢指针。
对撞指针:一般用于顺序结构中,也称左右指针。
• 对撞指针从两端向中间移动。一个指针从最左端开始,另一个从最右端开始,然后逐渐往中间逼近。
• 对撞指针的终止条件一般是两个指针相遇或者错开(也可能在循环内部找到结果直接跳出循环),也就是:
◦ left == right (两个指针指向同一个位置)
◦ left > right (两个指针错开)
快慢指针:又称为龟兔赛跑算法,其基本思想就是使用两个移动速度不同的指针在数组或链表等序列 结构上移动。 如果我们要研究的问题出现循环往复的情况时,均可考虑使用快 慢指针的思想。快慢指针的实现方式有很多种,最常用的一种就是:
• 在一次循环中,每次让慢的指针向后移动一位,而快的指针往后移动两位,实现一快一慢。
++注意:++这里的指针并不是C语言中学的 int*,char*的指针(地址),而是用变量记录数组下标(指针),变量++或--相当于指向 指针的移动。
【283.移动零】
1、题目描述

2、实现核心及思路
解题思路:
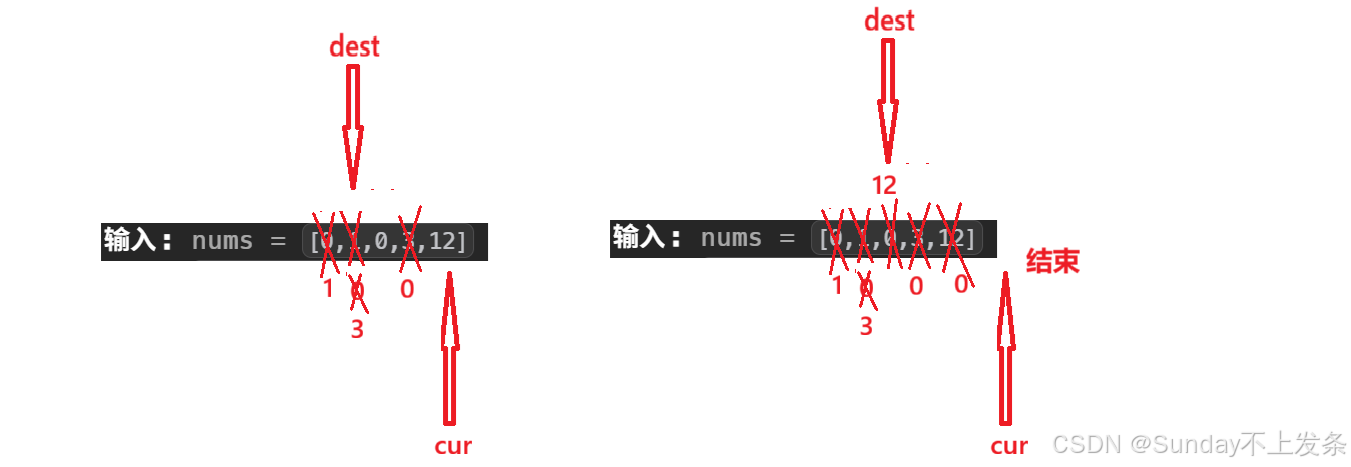
这里对撞指针(左右指针)的方案肯定是行不通的,因为题目要求移动 0 元素的同时还要保证非零元素的相对顺序。所以,我们采用两个指针都从数组的左端出发,把非零的元素依次找到放在前面,最后剩下 0 自然就排在数组后面了。
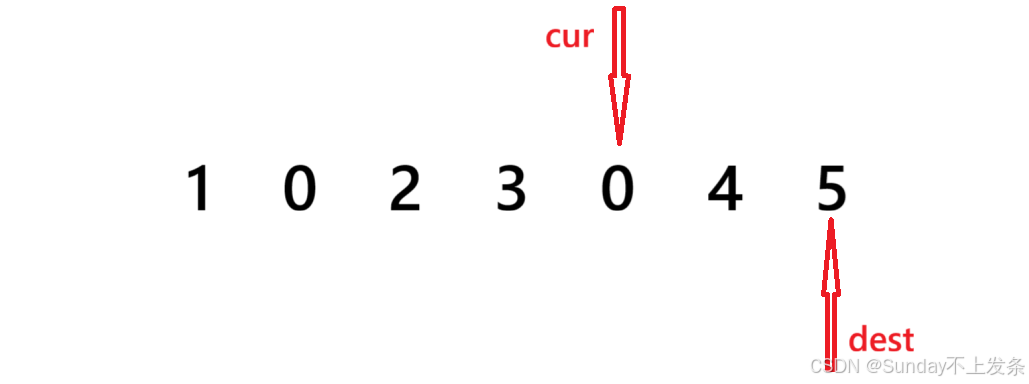
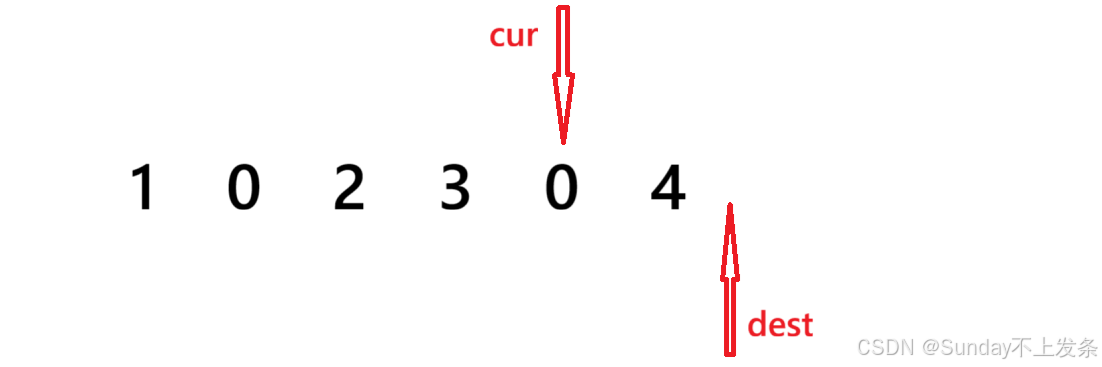
(1)刚开始让一个指针cur 先指向数组的第一个元素,另一个指针 dest 初始化为 -1。cur 用来找非零元素,dest 用来确定 cur 之前的 0 元素。
(2)当 cur 指向的元素为零则 cur++,继续向后找非零元素来将前面的 0 交换到后面;
(3)当 cur 指向的元素不为 0,则让 dest 向前移动一位(dest++),因为此时cur 之前的元素要么全为 0,要么dest 和 cur 指向同一个元素。然后,交换 cur 和 dest 指向的元素,cur 继续向后移动(cur++)。
(4)结束条件:当 cur 走到数组尾部的时候意味着所有非零元素都找到了,结束。
思路可视化:
代码实现:
cpp
class Solution {
public:
void moveZeroes(vector<int>& nums)
{
int size=nums.size();
// 定义双指针
int dest=-1;
int cur=0; // 指向数组第一个元素
while(cur<size)
{
// 找到非零元素
if(nums[cur]!=0)
{
dest++;
swap(nums[dest],nums[cur]);
}
cur++;
}
}
};代码测试:
cpp
int main()
{
Solution s;
vector<int> v1{ 1,0,2,0,3,0,4 };
vector<int> v2{ 0,0,0,6,5,4 };
s.moveZeroes(v1);
for (auto e : v1) { cout << e << " "; }
cout << endl;
s.moveZeroes(v2);
for (auto e : v2) { cout << e << " "; }
return 0;
}
【1089.复写零】
1、题目描述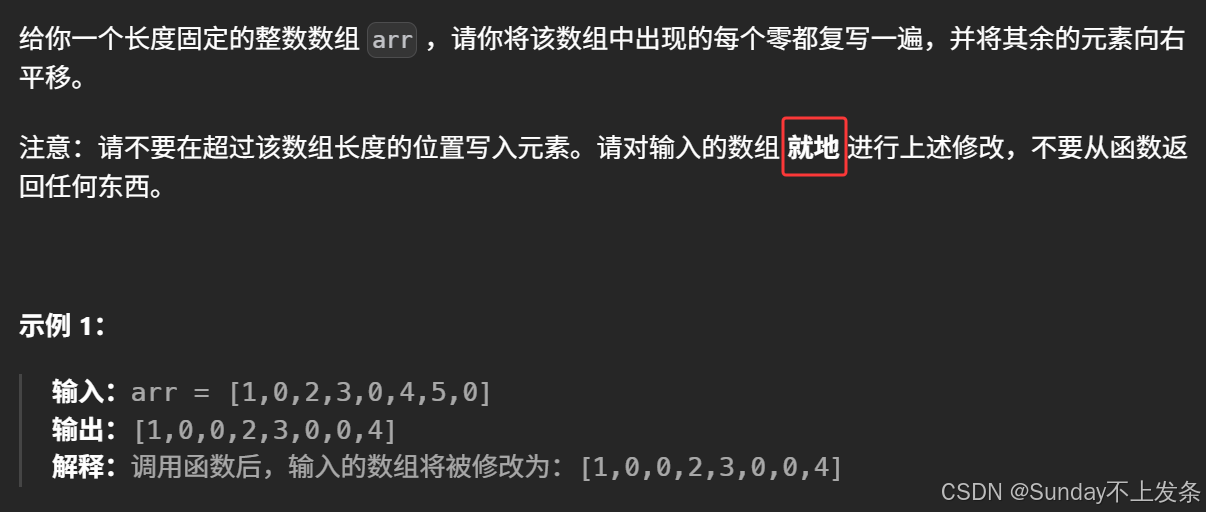
2、实现核心及思路
解题思路:
**解法一:**额外创建一个等大的数组,然后从头开始遍历原数组,遇到非零元素正常写入新数组,遇到 0 元素,写入两次,当新数组写满就终止。
这种解法肯定是我们第一时间想到的,但题目明确限制在原数组上操作。
**解法二:**观察示例1可知,最终的输出结果即将原来的5 和 0 覆盖了,因为复写了两个 0 元素。所以,我们只需要将 [1,0,2,3,0,4]这部分数据按要求进行复写零。但如果,我们从前往后遍历进行复写零时就会出现覆盖 0 元素后一个元素的问题,所以,我们考虑从 4 开始向前遍历数组来复写零,并把遍历到的元素从原数组的最后依次往左边放。非零元素写一次,0 元素写两次。
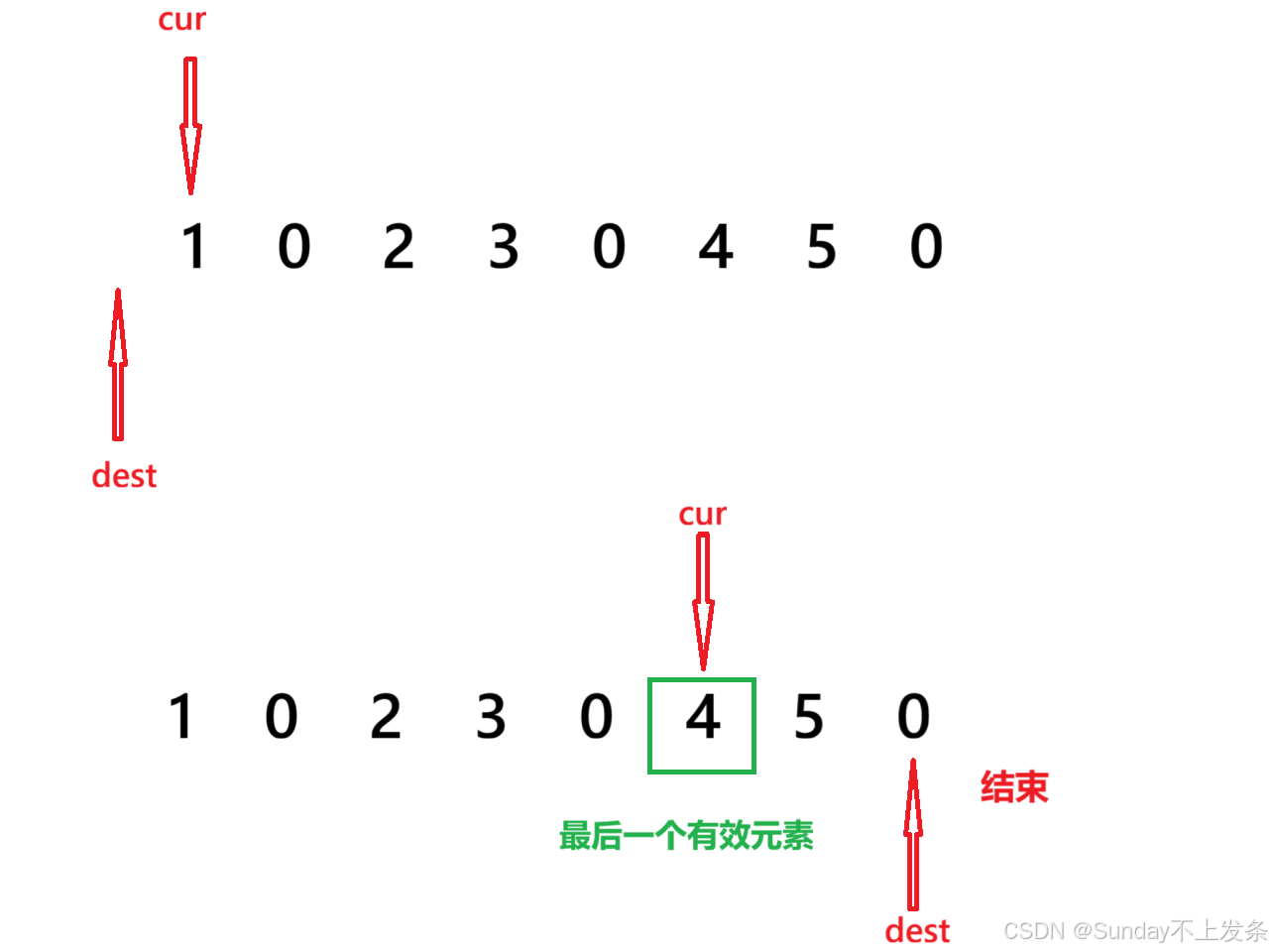
⭐️⭐️所以,我们的问题就转化为了:先找最后一个有效元素(相当于上面的" 4 "),然后从最后一个有效元素开始从后往前遍历复写零。
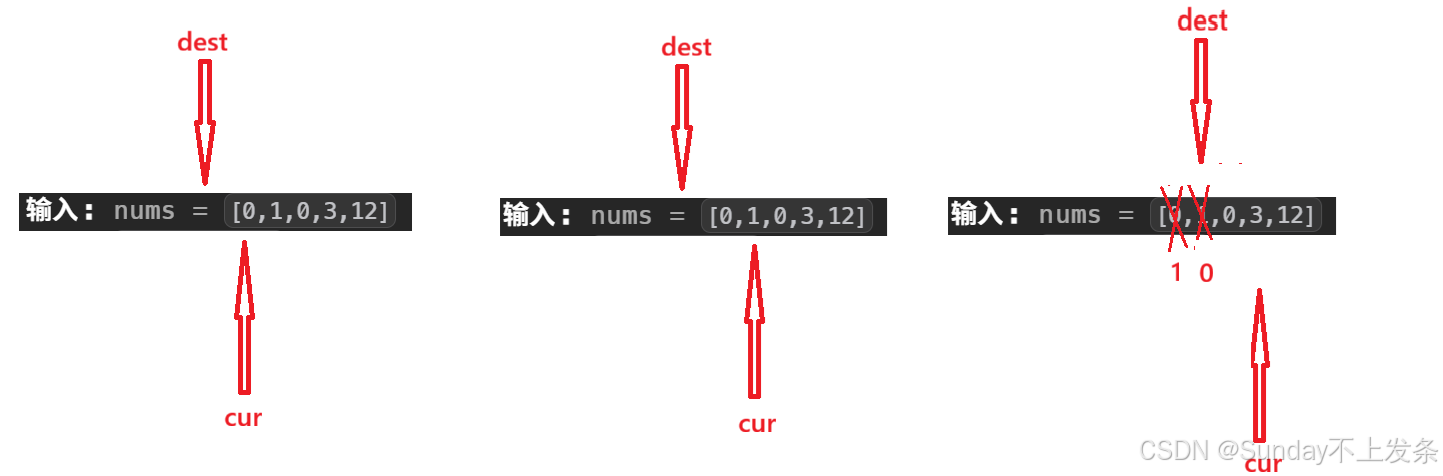
步骤一:利用双指针法找最后一个有效元素位置,让cur指针开始指向第一个元素,然后遍历数组,同时定义 dest指针(初始化为-1,即相当于指向数组起始位置的前一个位置)。当 cur 指向非零元素,left 向后移动一位,当 cur 指向零元素left 向后移动两位(即为复写零留出位置)。
结束条件:当 dest 指向的位置到数组的末尾时,即复写零后刚好能将数组写满。设数组大小为size,则dest < size - 1。
++细节一:++
面对这种情形,即当进入循环后发现dest 移动两次后到了数组的末尾,此时,我们不能再让cur 向前移动了,如果再移动数组空间大小就不够复写两个 0 了。所以,在 cur++ 之前我们还要判断dest 是否已经 不满足 dest < size - 1了。
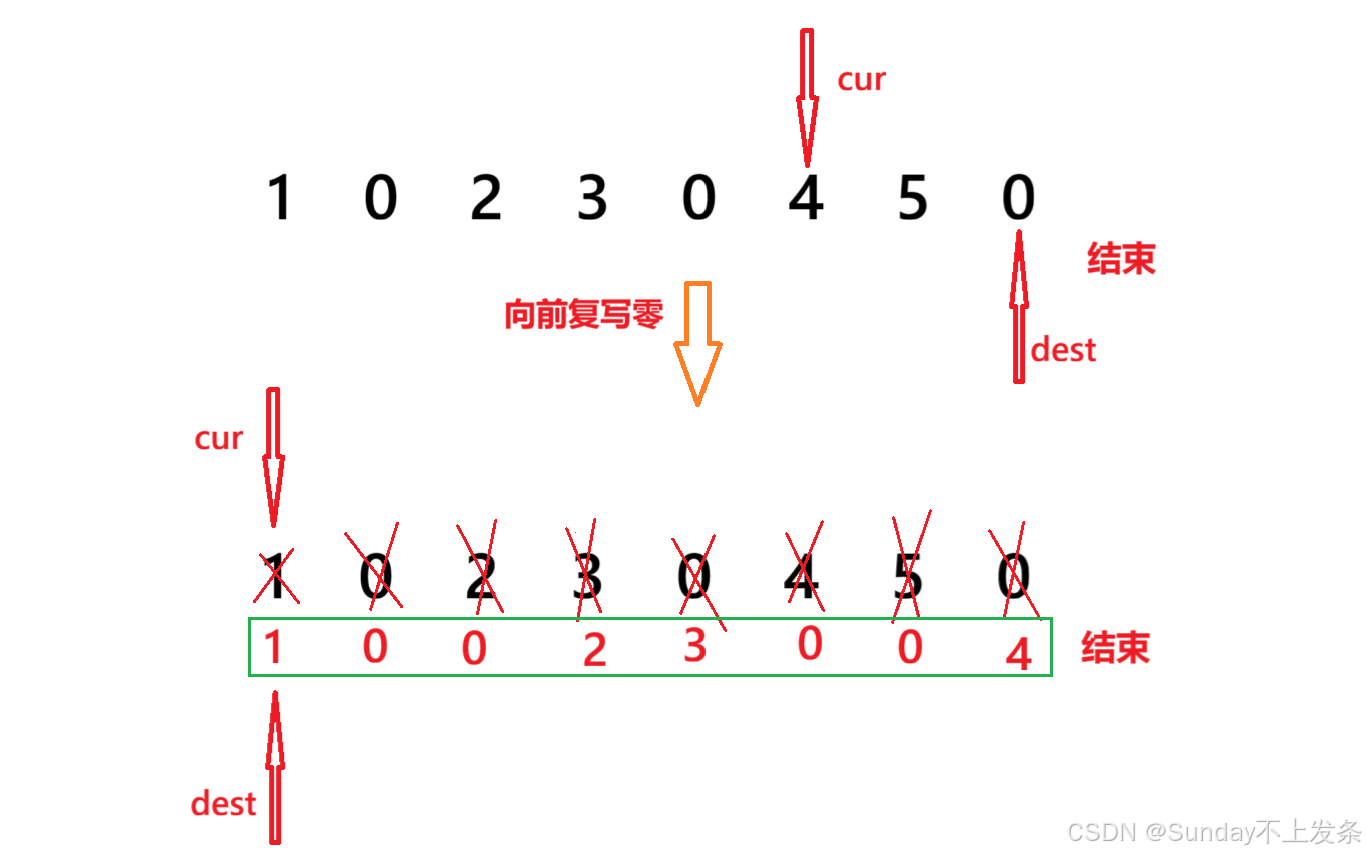
步骤二:继续利用双指针法,cur 指针已经指向了最后一个有效数据,所以让 dest 指向数组的最后。从 cur 指向的位置 开始向前遍历数组来复写零,当遍历到非零元素,dest 指向位置处仅将该元素写一次,然后 cur--,dest--,继续向前遍历;当遍历到 0 元素,dest 指向位置处先写一次 0 ,然后dest向左移动(dest--),并再写一次 0,然后 cur--,dest-- ... 以此类推。
结束条件:当 cur 遍历到数组的起始位置,即复写结束。cur >= 0
++细节二:++
当cur 指向最后一个有效数据且为 0 时,dest 需要向后移动两次,但是数组空间大小只剩下一个位置,即dest 出了数组。意味着我们在先前复写零时,cur 指向的这个 0 元素只能复写一次,所以,我们需要单独处理。
思路可视化:
代码实现:
cpp
class Solution {
public:
void duplicateZeros(vector<int>& arr)
{
int cur = 0; // 指向数组首元素
int dest = -1; // 指向数组开头之前
int size = arr.size();
while (dest < size - 1) // 结束条件:dest到数组末尾或之后
{
if (arr[cur] == 0) dest += 2; // 遍历到 0 元素,dest 向后移动两位
else
dest++; // 非零元素,dest 正常向后移动一位
if (dest < size - 1) cur++; // 细节一
}
if (dest >= size) // 细节二:处理最后一个 0 元素只复写一次
{
arr[size - 1] = 0;
dest = size - 2;
cur--;
}
while (cur >= 0) // 结束条件
{
if (arr[cur] == 0) // 复写零
{
arr[dest--] = 0;
arr[dest--] = 0;
}
else
arr[dest--] = arr[cur];
cur--; // 向前遍历
}
}
};代码测试:
cpp
int main()
{
Solution s;
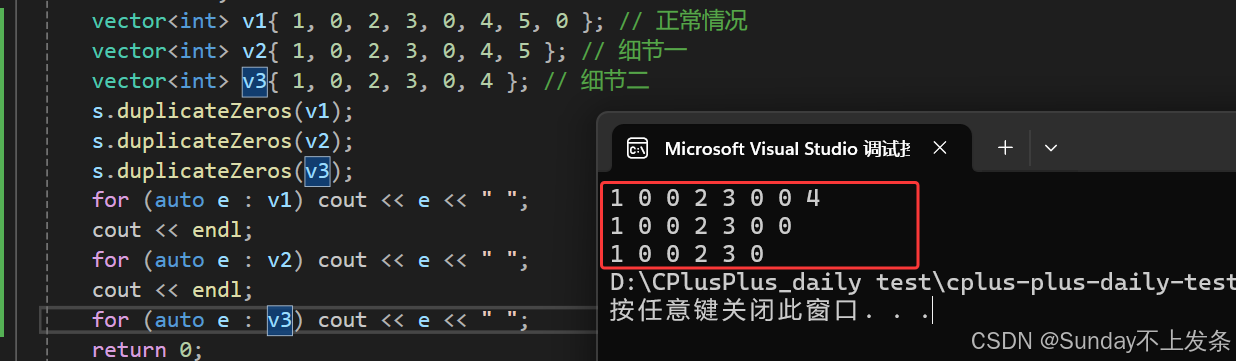
vector<int> v1{ 1, 0, 2, 3, 0, 4, 5, 0 }; // 正常情况
vector<int> v2{ 1, 0, 2, 3, 0, 4, 5 }; // 细节一
vector<int> v3{ 1, 0, 2, 3, 0, 4 }; // 细节二
s.duplicateZeros(v1);
s.duplicateZeros(v2);
s.duplicateZeros(v3);
for (auto e : v1) cout << e << " ";
cout << endl;
for (auto e : v2) cout << e << " ";
cout << endl;
for (auto e : v3) cout << e << " ";
return 0;
}
【202.快乐数】
1、题目描述

2、实现核心及思路
解题思路:

对于n = 19,经过求和后,最终结果变为了1,即19为快乐数;n = 2,经过求和,最终又回到了起点。
**结论:**对于每个非零整数,进行上面的操作,要么最终得到1,要么继续回到一个求和过程中的某一个值(非1),但不一定回到最开始(像2这样)。
即经过不断的求和(按上面的规则),最会进入到一个循环当中,得到1 的这种情况也不例外,1求和还是1,也是循环。而对于这种循环的问题:我们均可以用快慢指针的方法解决。

假设慢指针一次走一步,快指针一次走两步,那么快指针一定先入环,但由于两者的速度差,最终肯定会相遇(结束条件)。
这里我们先不做证明!!!(后面会补充)
对于这个题而言:慢指针走一步即对应一次求和一次,快指针走两步即对应连续求和两次。
结束条件:当快慢指针相遇。
然后判断:如果相遇时,快慢指针指向的和为 1 ,这个数即为快乐数;反之,则不是。
代码实现:
cpp
class Solution {
public:
// 求和函数
int Sum(int n)
{
int sum = 0;
while(n)
{
int a = n%10;
sum += pow(a,2);
n/=10;
}
return sum;
}
bool isHappy(int n)
{
int slow = Sum(n); // 慢指针
int fast = Sum(n); // 快指针
fast = Sum(fast);
while(slow != fast) // 结束条件
{
slow = Sum(slow);
fast = Sum(fast);
fast = Sum(fast);
}
if(slow == 1)
return true;
else
return false;
}
};【11.盛水最多容器】
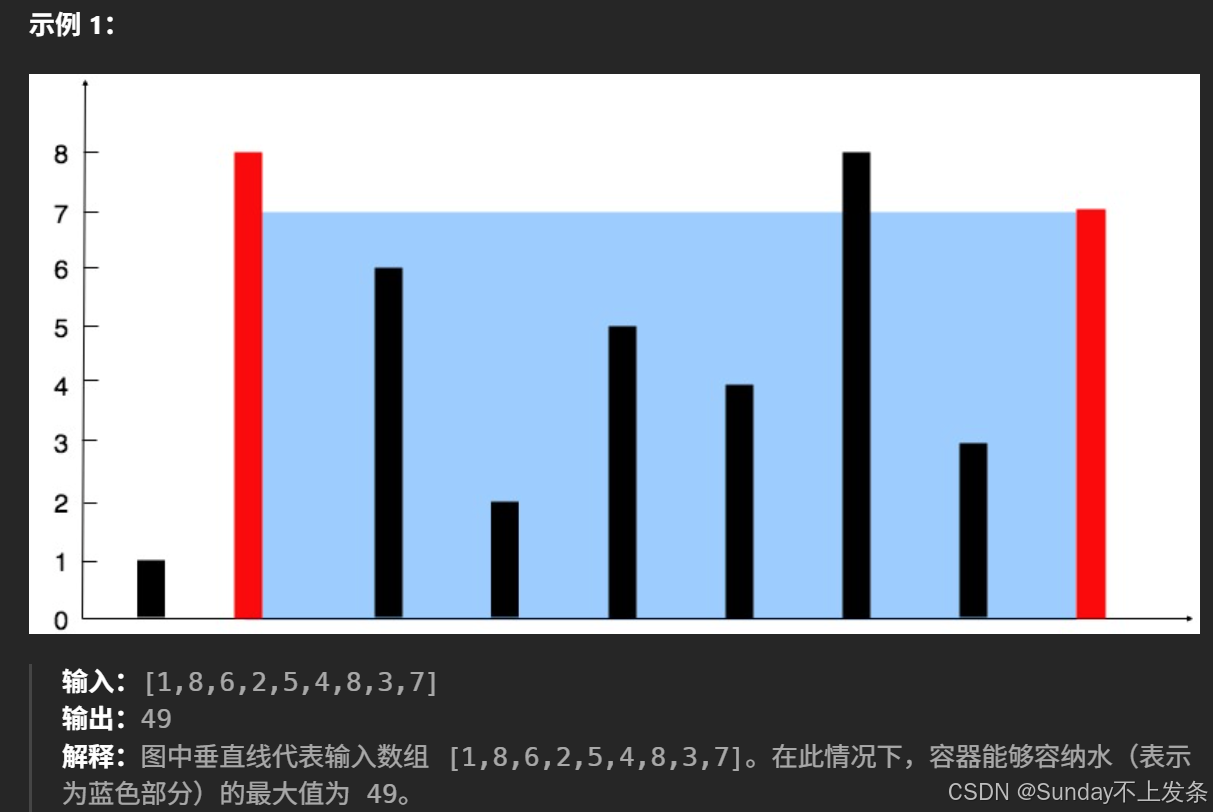
1、题目描述
2、实现核心及思路
解题思路:
***解法一:***暴力解法,两次for循环,算出所有的体积,找出最大值。
解法二: 对撞指针(左右指针),left 和 right 指针向右向左找符合的桶(区间)。主要是依靠单调性,当left 和 right 向内移动时,宽度一定是变短的,体积 V = 宽度 * 高,所以要想找到最大的体积,只能依靠找到更大的高度。
所以,让left 和 right 中指向高度较小的一个向内移动, 找更大的高度,才有可能使体积更大。
同时,每次计算一个体积,通过比较获得最大体积。
💡库当中有一个 max 函数可以帮我们找两个数中的较大值,头文件<algorithm>
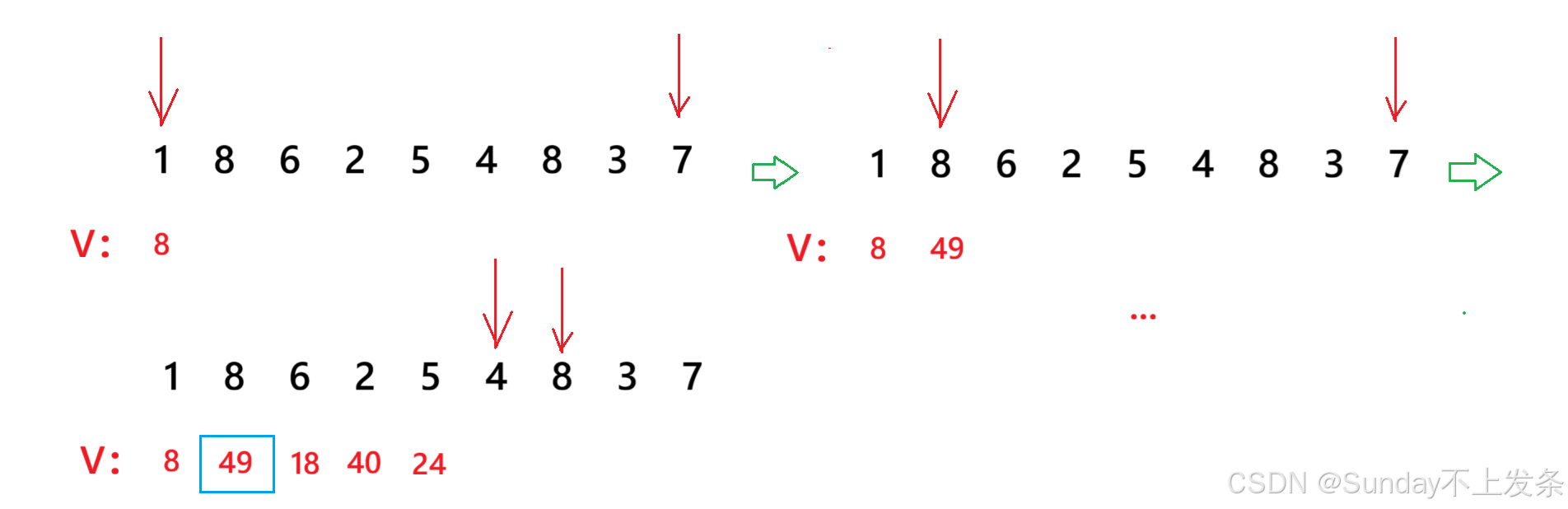
思路可视化:
代码实现:
cpp
class Solution {
public:
int maxArea(vector<int>& height)
{
int left = 0; // 左指针
int right = height.size() - 1; // 右指针
int m = 0;
while(left < right)
{
int h = height[left] > height[right] ? height[right] : height[left]; // 找较小边
int V = (right - left) * h; // 计算体积
m = max(m,V); // 更新体积的值
if(height[left] < height[right]) left++;
else right--;
}
return m;
}
};