本文涉及知识点
计算几何
四种定义
线段定义:多边形P是凸多边形当且仅当 ∀ A , B ∈ P \forall A,B \in P ∀A,B∈P,线段AB都在P内。
内角定义:严格凸,多边形的内角 < 18 0 ∘ <180^\circ <180∘。容许平角:多边形的内角 ≤ 18 0 ∘ \le 180^\circ ≤180∘。
转向相同:令端点顺时针(逆时针)依次为 P 0 , P 1 ⋯ P n − 1 P_0,P_1\cdots P_{n-1} P0,P1⋯Pn−1,令 P 0 = P n , P 1 = = P n P_0=P_n,P_1==P_n P0=Pn,P1==Pn。
P i P i + 1 ⃗ × P i + 1 P i 2 ⃗ , 0 < i < n \vec {P_iP_{i+1}} \times \vec{ P_{i+1}P_{i_2}},0<i<n PiPi+1 ×Pi+1Pi2 ,0<i<n符号相同。
半平面:多边形可以表示为有限个半平面的交集,且每个边所在的直线定义一个包含整个多边形的半平面。
半平面
通过直线定义:
ax+by < c 和ax+by > c。都是开半平面。
ax+by ≥ \ge ≥c和ax+by ≤ \le ≤ c都是闭半平面。
ax+by>c ⟺ \iff ⟺ -ax-by<-c。
通过向量定义:
已知点P和方向向量 v ⃗ \vec v v ,X是点 P ⃗ X × v ≤ 0 \vec PX \times v \le 0 P X×v≤0
定义一 → \rightarrow → 定义二
连通内角和超过 18 0 ∘ 180^\circ 180∘的顶点B,B的相邻顶点AC。除AC外,线段上的其它点多在多边形外。

定义二 → \rightarrow → 定义一
用数学归纳法证明。三角形一定符合。如果n(n>3)个顶点。如果AB全部在 △ a b c \triangle abc △abc,则证毕。如果AB全部不在 △ a b c \triangle abc △abc中,用边ac代替ab、bc。n-=1,待证明不变。如果AB和ac相交于C,不失一般性,令A在三角形内,则AC全部在三角形内,用边ac代替ab、bc。
定义二 ⟺ \iff ⟺定义三,
这个好理解,不赘述。
定义三 → \rightarrow → 定义四
证明过程较复杂,暂且放放。
定义四 → \rightarrow → 定义一

对每个半平面单独处理,以半平面的分界直线为新坐标的x轴,AC所在为y轴正方向。
P(- ∞ , 0 ) \infty,0) ∞,0)。则 ∠ X P A < ∠ X P B < ∠ X P C \angle XPA < \angle XPB <\angle XPC ∠XPA<∠XPB<∠XPC,故B一定在同一个半平面。
定义一 → \rightarrow → 定义四
性质一 :P在任意边所在直线的一侧。
假定P在直线AB两侧都有点。旋转平移简单多边形P,使得边AB和y轴重合,且原点在AB上。
由于AB是边界线,故P1(-无穷小,0)和P2(无穷小,0)一个在P内,一个在P外。不失一般性,令后者在P内。令在AB左边的点是P3,根据定义P3,P2在P内,线段P3P2上的点全部在P内,即(-无穷小,y0)也在P内,而(无穷小,y0)也在P内,和边界线两则一个在P内,一个在P外,矛盾。
P边所在的直线构成的平面集便是定义四。
反例
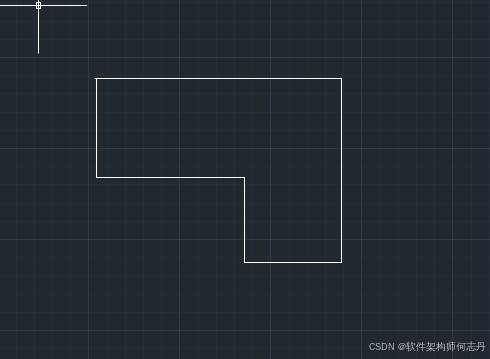
这个凹多边形,无法通过半平面集表示。
水平排除左下,右下也排除了。
竖直排除左下,左上也排除了。

扩展阅读
| 我想对大家说的话 |
|---|
| 工作中遇到的问题,可以按类别查阅鄙人的算法文章,请点击《算法与数据汇总》。 |
| 学习算法:按章节学习《喜缺全书算法册》,大量的题目和测试用例,打包下载。重视操作 |
| 有效学习:明确的目标 及时的反馈 拉伸区(难度合适) 专注 |
| 员工说:技术至上,老板不信;投资人的代表说:技术至上,老板会信。 |
| 闻缺陷则喜(喜缺)是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
| 失败+反思=成功 成功+反思=成功 |
视频课程
先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法 用**C++**实现。
