基于萤火虫算法优化BP神经网络(FA - BP)实现多输出数据回归预测

基于萤火虫算法优化BP神经网络(FA-BP)的多输出数据回归预测FA-BP多输出数据回归 matlab代码注：暂无Matlab版本要求--推荐2018B版本及以上

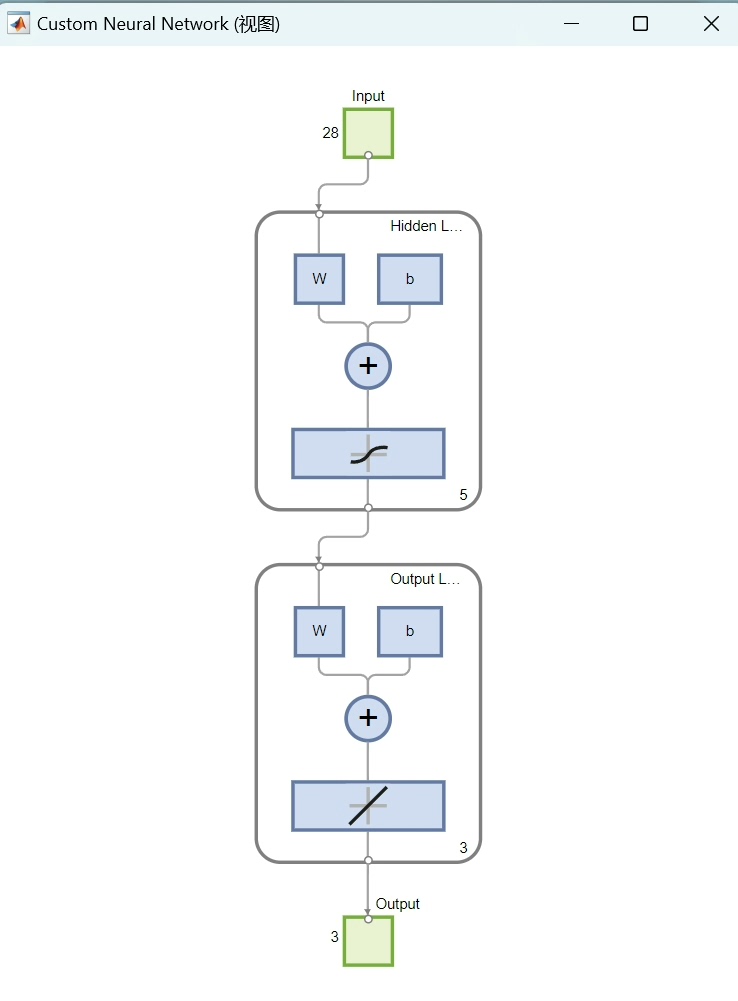
在数据预测领域，BP神经网络是一种常用且有效的模型，但它容易陷入局部最优解。而萤火虫算法（Firefly Algorithm，FA）具有较强的全局搜索能力，将两者结合（FA - BP）可以提升多输出数据回归预测的性能。下面我们就来看看如何使用Matlab实现基于FA - BP的多输出数据回归预测。

1. BP神经网络基础

BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络。在Matlab中，搭建一个简单的BP神经网络示例代码如下：

matlab 复制代码

% 创建一个简单的BP神经网络
inputLayerSize = 2; % 输入层神经元个数
hiddenLayerSize = 10; % 隐藏层神经元个数
outputLayerSize = 1; % 输出层神经元个数
net = feedforwardnet(hiddenLayerSize);
net.inputs{1}.size = inputLayerSize;
net.outputs{2}.size = outputLayerSize;

这段代码中，我们先定义了输入层、隐藏层和输出层的神经元个数，然后使用feedforwardnet函数创建了一个前馈神经网络net，并根据我们设定的神经元个数调整了网络输入和输出的大小。

2. 萤火虫算法原理

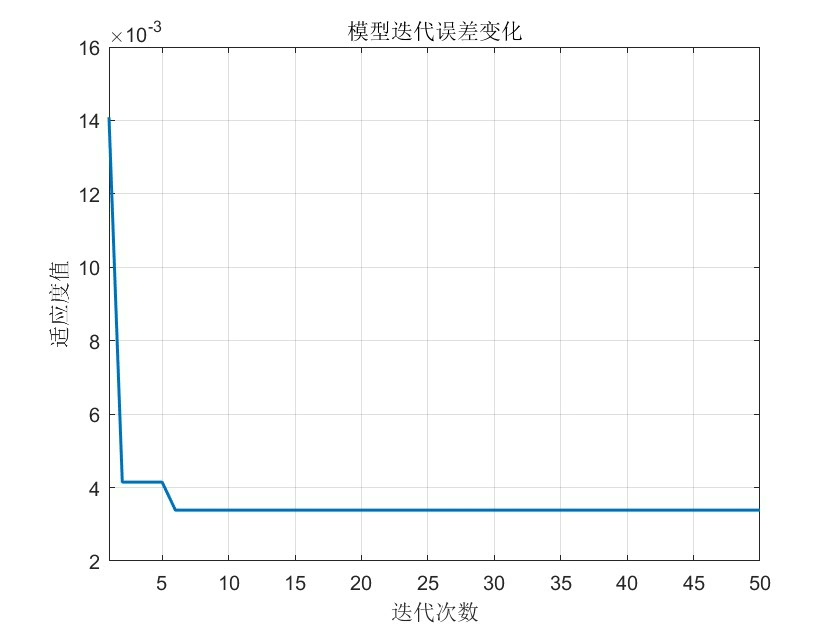
萤火虫算法模拟了萤火虫发光吸引同伴靠近的行为。在优化问题中，每个萤火虫代表一个可能的解，萤火虫的亮度对应解的质量（适应度）。较亮的萤火虫会吸引较暗的萤火虫向其移动，通过不断迭代，萤火虫逐渐向全局最优解聚集。

3. FA - BP实现多输出数据回归预测Matlab代码

数据准备

假设我们有一个多输入多输出的数据集，以下是简单的数据加载与划分示例：

matlab 复制代码

% 加载数据，假设数据文件名为data.mat
load('data.mat'); 
inputData = data(:, 1:end - 2); % 输入数据，假设最后两列为输出
outputData = data(:, end - 1:end); 

% 划分训练集和测试集
[trainInd, testInd] = dividerand(size(inputData, 1), 0.7, 0.3);
trainInput = inputData(trainInd, :);
trainOutput = outputData(trainInd, :);
testInput = inputData(testInd, :);
testOutput = outputData(testInd, :);

这里我们从data.mat文件加载数据，将数据划分为输入和输出部分，然后按照70%训练集，30%测试集的比例进行划分。

萤火虫算法优化BP神经网络

matlab 复制代码

% 定义萤火虫算法参数
n = 50; % 萤火虫数量
maxGen = 100; % 最大迭代次数
alpha = 0.2; % 步长因子
beta0 = 1; % 光吸收系数
gamma = 1; % 亮度衰减系数

% BP神经网络参数
inputLayerSize = size(inputData, 2);
hiddenLayerSize = 15;
outputLayerSize = size(outputData, 2);

% 初始化萤火虫位置（对应BP神经网络的权重和阈值）
fireflies = zeros(n, (inputLayerSize * hiddenLayerSize + hiddenLayerSize) + (hiddenLayerSize * outputLayerSize + outputLayerSize));
for i = 1:n
    fireflies(i, :) = randn(1, (inputLayerSize * hiddenLayerSize + hiddenLayerSize) + (hiddenLayerSize * outputLayerSize + outputLayerSize));
end

% 迭代优化
for gen = 1:maxGen
    % 计算适应度（这里使用BP神经网络预测误差作为适应度）
    fitness = zeros(n, 1);
    for i = 1:n
        net = createNet(fireflies(i, :), inputLayerSize, hiddenLayerSize, outputLayerSize);
        trainResult = sim(net, trainInput');
        fitness(i) = sum(sum((trainResult - trainOutput').^2));
    end

    % 更新萤火虫位置
    for i = 1:n
        for j = 1:n
            if fitness(i) > fitness(j)
                r = norm(fireflies(i, :) - fireflies(j, :));
                beta = beta0 * exp(-gamma * r^2);
                fireflies(i, :) = fireflies(i, :) + beta * (fireflies(j, :) - fireflies(i, :)) + alpha * (randn(size(fireflies(i, :))));
            end
        end
    end
end

% 根据最优萤火虫位置创建最终的BP神经网络
[~, bestIndex] = min(fitness);
bestWeights = fireflies(bestIndex, :);
finalNet = createNet(bestWeights, inputLayerSize, hiddenLayerSize, outputLayerSize);

在这段代码中，我们首先定义了萤火虫算法的参数，包括萤火虫数量、最大迭代次数等。然后初始化了萤火虫的位置，这些位置实际上对应BP神经网络的权重和阈值。在每次迭代中，我们计算每个萤火虫的适应度，这里以BP神经网络在训练集上的预测误差作为适应度。然后根据萤火虫之间的亮度关系（适应度大小）更新萤火虫的位置。最后根据最优萤火虫的位置创建最终的BP神经网络。

创建BP神经网络函数

matlab 复制代码

function net = createNet(weights, inputLayerSize, hiddenLayerSize, outputLayerSize)
    net = feedforwardnet(hiddenLayerSize);
    net.inputs{1}.size = inputLayerSize;
    net.outputs{2}.size = outputLayerSize;

    % 设置权重和阈值
    start = 1;
    end1 = inputLayerSize * hiddenLayerSize;
    IW = reshape(weights(start:start + end1 - 1), hiddenLayerSize, inputLayerSize);
    start = start + end1;
    end2 = hiddenLayerSize;
    b1 = weights(start:start + end2 - 1)';
    start = start + end2;
    end3 = hiddenLayerSize * outputLayerSize;
    LW = reshape(weights(start:start + end3 - 1), outputLayerSize, hiddenLayerSize);
    start = start + end3;
    end4 = outputLayerSize;
    b2 = weights(start:start + end4 - 1)';

    net.IW{1, 1} = IW;
    net.b{1} = b1;
    net.LW{2, 1} = LW;
    net.b{2} = b2;
end

这个函数根据传入的权重和阈值创建BP神经网络。它从权重向量中提取输入层到隐藏层的权重IW、隐藏层阈值b1、隐藏层到输出层的权重LW以及输出层阈值b2，并将它们设置到创建的BP神经网络中。

预测与评估

matlab 复制代码

% 预测
testResult = sim(finalNet, testInput');

% 评估指标
mse = mean(mean((testResult - testOutput').^2));
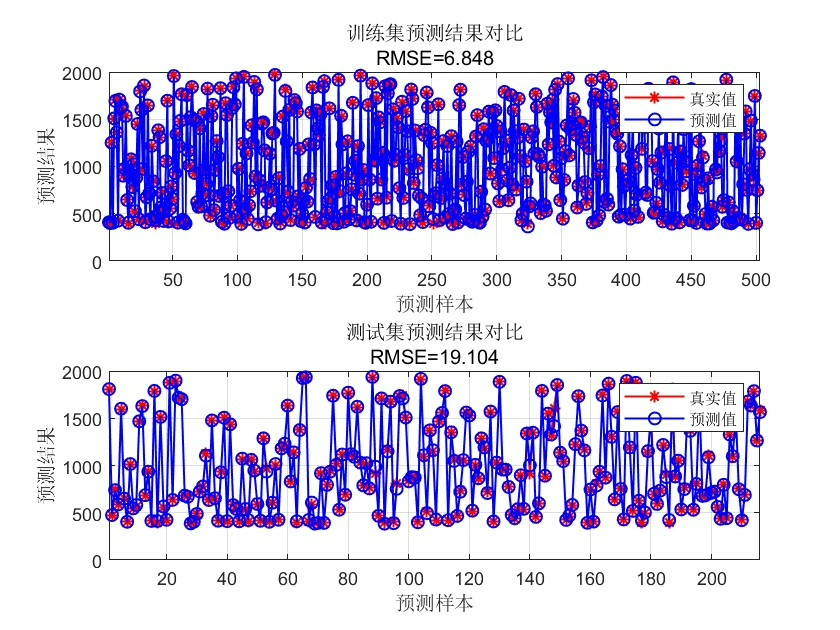
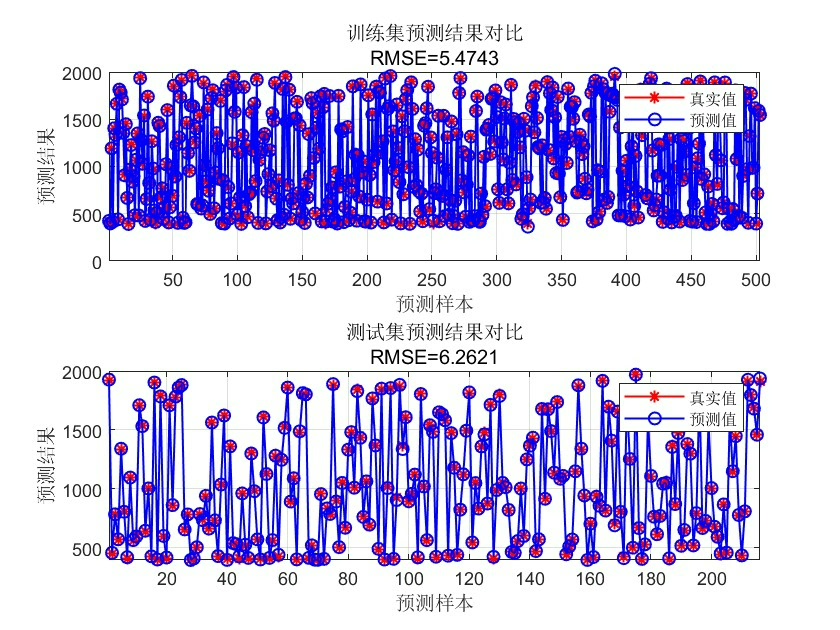
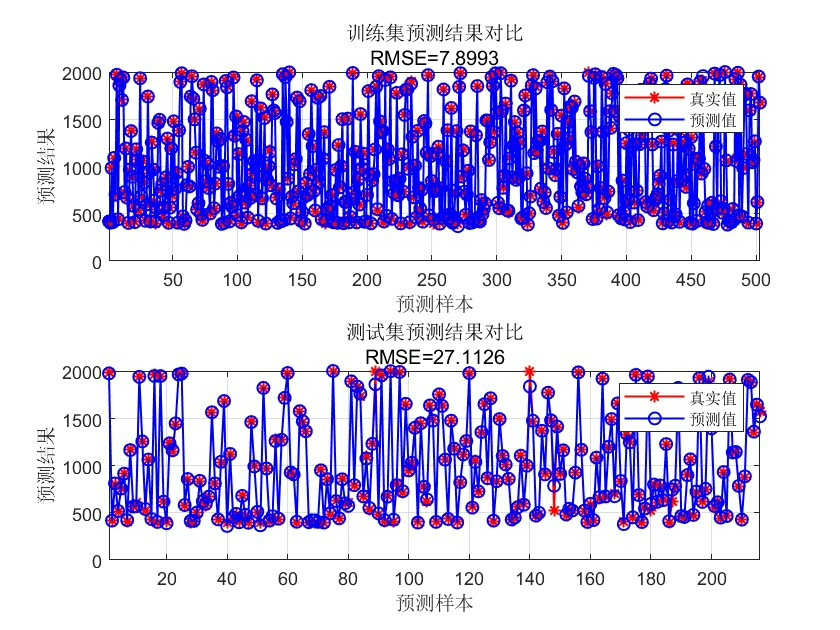
rmse = sqrt(mse);

最后，我们使用最终的FA - BP神经网络对测试集进行预测，并计算均方误差（MSE）和均方根误差（RMSE）来评估预测性能。

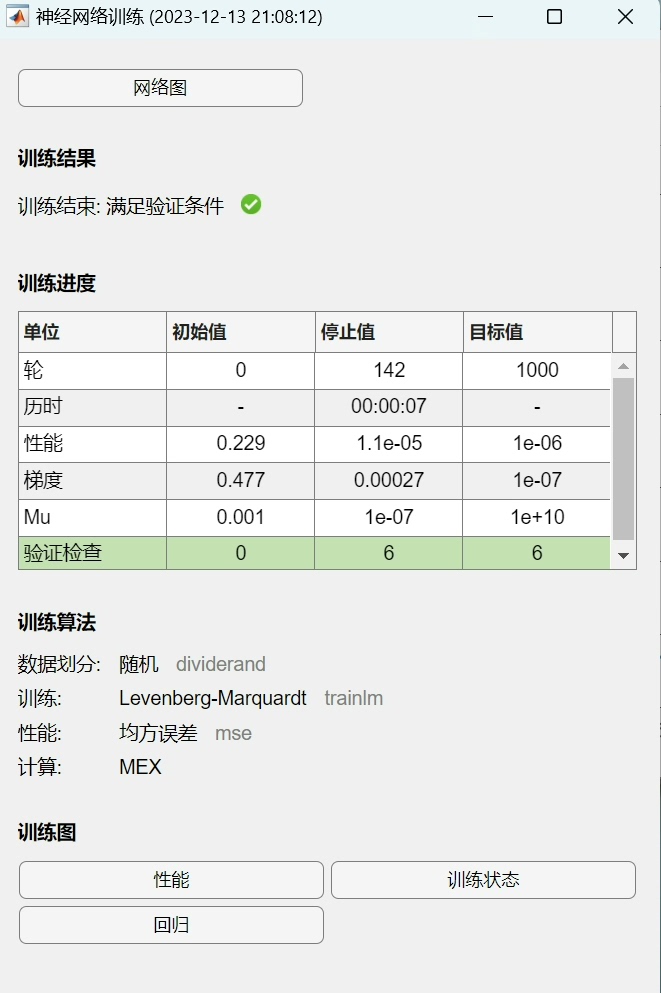
通过以上Matlab代码实现，我们利用萤火虫算法优化了BP神经网络，提升了多输出数据回归预测的效果。希望这篇博文能帮助你在相关领域的研究和应用中有所收获。