【牛客BM30】二叉搜索树与双向链表:java中以引用代指针操作的艺术与陷阱
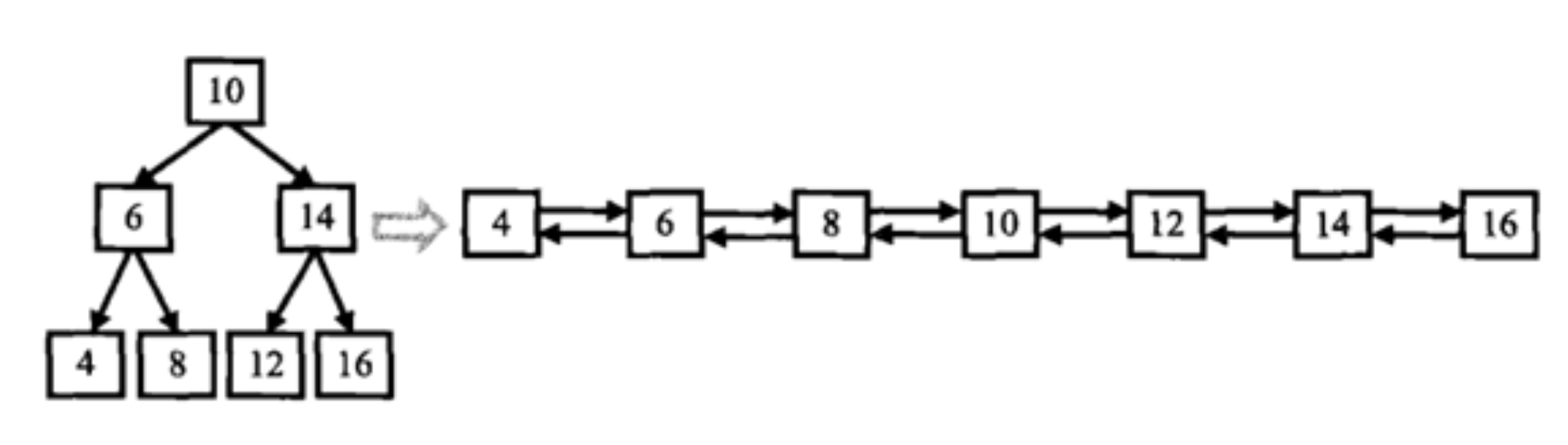
在数据结构面试中,"将二叉搜索树(BST)转换成有序的双向链表" 是一道考察指针操作、递归思维以及边界条件处理的经典题目。
题目要求我们在 O(1)O(1)O(1) 空间复杂度 (原地操作)下完成转换,这意味着我们不能创建新节点,只能改变原有树节点 left 和 right 指针的指向。
今天我们就来拆解这个问题的核心思路,并复盘一个容易被忽视的"空指针陷阱"。
1. 核心思路:中序遍历 + 全局前驱
为什么是中序遍历?
二叉搜索树(BST)的一个核心性质是:其中序遍历(左 -> 根 -> 右)的结果是严格递增有序的 。
题目要求生成的双向链表也是有序的。因此,解题的大框架必然是中序遍历。
怎么把树变成链表?
我们需要在遍历的过程中,修改节点的指针。
- 树节点的
left指针 →\rightarrow→ 双向链表的prev指针。 - 树节点的
right指针 →\rightarrow→ 双向链表的next指针。
关键变量:prev
为了将当前节点(cur)与前一个遍历到的节点连接起来,我们需要一个全局变量 prev 来记录**"在中序遍历中,上一个访问完的节点"**。
算法流程(非常类似中序遍历的递归写法)
只不过中序遍历是在递归左子树和右子树之间加上System.out.print("root.val" +" ");
而由图可以看出来,这二叉树转的双向链表顺序明显满足中序遍历。
- 递归左子树:先处理左边,把左边已经转换好。
- 处理当前节点(连接操作) :
- 将当前节点
root的左指针指向prev(root.left = prev)。 - 如果
prev不为空,将prev的右指针指向当前节点 (prev.right = root)。 - 更新
prev:当前节点处理完毕,它变成了下一个节点的"前驱",所以prev = root。
- 将当前节点
- 递归右子树:继续处理右边。
2. 代码深度解析
java
public class Solution {
// 全局变量,记录中序遍历过程中"上一个"处理过的节点
TreeNode prev = null;
public TreeNode Convert(TreeNode pRootOfTree) {
// 【问题核心】为什么要单独判断空?后面会详细解答
if(pRootOfTree == null) return null;
// 1. 执行中序遍历,修改指针
ConvertChild(pRootOfTree);
// 2. 寻找链表头节点
// 转换完后,pRootOfTree 还在树的根节点位置(也就是链表的中间某处)
// 双向链表的头节点应该是"最左侧"的节点
TreeNode head = pRootOfTree;
while(head.left != null){
head = head.left;
}
return head;
}
// 辅助函数:标准的中序遍历框架
public void ConvertChild(TreeNode root){
if(root == null) return; // 递归终止条件
// 1. 递归左子树
ConvertChild(root.left);
// 2. 核心连接逻辑
root.left = prev; // 当前节点的左指针指向前驱
if(prev != null){
prev.right = root; // 前驱的右指针指向当前节点(双向绑定)
}
prev = root; // 移动 prev 指针,当前节点成为下一个节点的前驱
// 3. 递归右子树
ConvertChild(root.right);
}
}3. 灵魂拷问:为什么必须在 Convert 中加判空?
这是本题最容易踩坑的地方。
问题描述 :
明明在 ConvertChild 函数的第一行已经写了 if(root == null) return;,为什么在主函数 Convert 开头不加 if(pRootOfTree == null) return null; 就会导致部分测试用例(空树)不通过?
详细解答 :
这里的判空不是为了防止递归出错,而是为了防止后续寻找头节点时的空指针异常。
让我们模拟一下输入为空树 {} 的情况:
- 假设没有
Convert函数里的判空。 - 输入
pRootOfTree为null。 - 调用
ConvertChild(null)。进入辅助函数,触发if(root == null) return;,函数直接结束,没问题。 - 回到
Convert主函数,继续往下执行。 - 执行
TreeNode head = pRootOfTree;,此时head被赋值为null。 - 执行
while(head.left != null)。- 程序试图访问
null.left。 - 💥 崩!抛出
java.lang.NullPointerException。
- 程序试图访问
结论 :
ConvertChild 中的判空是递归的终止条件 (Base Case),它保证了递归能正常结束。
而 Convert 中的判空是防御性编程 ,它保护了后续寻找 head 的逻辑(head.left)不操作空对象。
如果不加这一句,当输入是空树时,程序会在寻找头节点时崩溃。
4. 寻找头节点的两种策略
在代码中,我们通过 while 循环往左走来寻找头节点。其实还有一种不需要循环的方法:
由于 prev 在遍历结束后会指向链表的尾节点 (中序遍历的最后一个节点),我们可以利用 prev 一路往左推(利用 left 指针),或者记录最开始的 head。
但在本题的结构下,直接从 pRootOfTree 往左找 head 是最直观的,因为转换后的链表依然保持了 left 指向更小元素的特性。
5. 总结
这道题考察了三个核心点:
- 理解 BST 性质:中序遍历即有序。
- 双指针操作 :在遍历过程中动态修改
left和right,像缝衣服一样把节点串起来。 - 鲁棒性 :处理
input == null的边界情况,避免后续逻辑空指针异常。