解密GPT的生成魔法：自回归模型

Niuguangshuo2025-12-16 14:22

当你和AI聊天时，它回答的每句话，其实都是一个字一个字"猜"出来的。它只做一件事：根据已经说出的所有字，猜出下一个最可能的字。

你问："今天天气？"

AI心里在猜：看到"今天天气" → 猜下一个是 "很" 。看到"今天天气很" → 猜下一个是 "好" 。看到"今天天气很好" → 猜下一个是 "。"于是回答诞生了："今天天气很好。"

这个"每次只猜下一个字"的简单规则，就是自回归模型。它支撑着所有智能对话AI的回答。

一、自回归模型

1.1 核心公式：概率的链条

自回归模型的核心思想可以用一个优雅的公式表达：

P ( x 1 , x 2 , . . . , x T ) = ∏ t = 1 T P ( x t ∣ x 1 , x 2 , . . . , x t − 1 ) P(x_1, x_2, ..., x_T) = \prod_{t=1}^{T} P(x_t | x_1, x_2, ..., x_{t-1}) P(x1,x2,...,xT)=t=1∏TP(xt∣x1,x2,...,xt−1)

分解理解：

  • x 1 , x 2 , . . . , x T x_1, x_2, ..., x_T x1,x2,...,xT 表示一个由T个词组成的序列
  • P ( x 1 , x 2 , . . . , x T ) P(x_1, x_2, ..., x_T) P(x1,x2,...,xT) 是这个序列出现的概率
  • P ( x t ∣ x 1 , x 2 , . . . , x t − 1 ) P(x_t | x_1, x_2, ..., x_{t-1}) P(xt∣x1,x2,...,xt−1) 是在给定前t-1个词的条件下，第t个词出现的概率
  • ∏ \prod ∏ 表示连乘，将所有条件概率相乘得到整个序列的概率

直观例子 ：对于句子"我爱学习"
P ( 我, 爱, 学习 ) = P ( 我 ) × P ( 爱 ∣ 我 ) × P ( 学习 ∣ 我, 爱 ) P(\text{我, 爱, 学习}) = P(\text{我}) \times P(\text{爱} | \text{我}) \times P(\text{学习} | \text{我, 爱}) P(我, 爱, 学习)=P(我)×P(爱∣我)×P(学习∣我, 爱)

1.2 自回归的条件概率分解

在深度学习中，我们通过神经网络参数化这个条件概率：
P ( x t ∣ x 1 , . . . , x t − 1 ) = Softmax ( f θ ( x 1 , . . . , x t − 1 ) ) P(x_t | x_1, ..., x_{t-1}) = \text{Softmax}(f_\theta(x_1, ..., x_{t-1})) P(xt∣x1,...,xt−1)=Softmax(fθ(x1,...,xt−1))

其中：

  • f θ f_\theta fθ 是参数为θ的神经网络（如Transformer）
  • Softmax函数将网络输出转换为概率分布
  • 模型在每一步输出一个在词汇表上的概率分布

二、训练数据构建

2.1 准备训练材料：海量文本

想象我们要训练AI理解中文，就需要准备一个庞大的"语料库"------这就像给AI准备的"语文课本"，包含了各种类型的文本： 新闻文章、小说、百科知识、社交媒体对话、论坛讨论、学术论文、技术文档、诗歌、歌词、剧本...

处理过程如下：

  1. 收集文本：从各种渠道获取海量文字
  2. 清洗整理：去掉错别字、乱码、无关内容
  3. 分词处理：将连续的文字切成有意义的单元

2.2 核心技巧：向右位移

训练自回归模型的关键在于如何教AI玩"猜词游戏"。我们通过"向右位移"的方法，将一句话拆解成多个"猜词"练习。

工作原理很简单 ：

给定一个完整的句子序列，我们构建：

  • 输入：从第一个词到倒数第二个词
  • 目标：从第二个词到最后一个词

用公式表示：
给定序列: [ x 1 , x 2 , x 3 , x 4 , x 5 ] \text{给定序列: }[x_1, x_2, x_3, x_4, x_5] 给定序列: [x1,x2,x3,x4,x5]
输入: [ x 1 , x 2 , x 3 , x 4 ] \text{输入: }[x_1, x_2, x_3, x_4] 输入: [x1,x2,x3,x4]
目标: [ x 2 , x 3 , x 4 , x 5 ] \text{目标: }[x_2, x_3, x_4, x_5] 目标: [x2,x3,x4,x5]

假设我们的句子是："机器学习是人工智能的重要分支"

第一步：分词处理

首先将这句话切割成有意义的单元（token）：

python 复制代码 
['机器', '学习', '是', '人工', '智能', '的', '重要', '分支']

第二步：添加特殊标记

为了让AI知道一句话从哪里开始、到哪里结束，我们添加两个特殊标记：

  • <BOS>：序列开始（Beginning of Sequence）
  • <EOS>：序列结束（End of Sequence）

添加后的完整序列：

python 复制代码 
[<BOS>, 机器, 学习, 是, 人工, 智能, 的, 重要, 分支, <EOS>]

第三步：向右位移构建训练对

输入（AI看到的） 目标（AI要猜的） 训练目标
[] [机器] 根据开始标记，猜第一个词是"机器"
[, 机器] [学习] 根据"机器"，猜下一个是"学习"
[, 机器, 学习] [是] 根据"机器学习"，猜下一个是"是"
... ... ...
[, 机器, 学习, 是, 人工, 智能, 的, 重要, 分支] [] 根据完整句子，猜下一个是结束标记

第四步：实际训练处理

在实际训练中，我们不是创建多个独立训练对，而是用一次性构建的方式：

  • 输入：[<BOS>, 机器, 学习, 是, 人工, 智能, 的, 重要, 分支]
  • 目标：[机器, 学习, 是, 人工, 智能, 的, 重要, 分支, <EOS>]

为什么可以一次性构建：

  • Transformer的并行架构：可以同时处理序列的所有位置
  • 因果掩码：确保每个位置只看到前面的信息，保持因果性
    高效训练：一次前向传播完成所有时间步的学习
    数学等价：一次性训练与传统逐位训练数学上等价

简单来说：Transformer就像一个"多任务学习"模型，一次性学习所有"基于前文预测下一个词"的任务，但通过因果掩码确保每个预测只依赖于前面的内容。

第五步：滑动窗口：处理长文本的关键

在实际应用中，我们通常面对的是很长的文本，比如一篇文章、一本书。这时候就不能用"向右位移"的方法处理整个文本了，为此，我们引入了滑动窗口技术。滑动窗口包含两个关键参数：

  1. 窗口长度：每次能看到多少个词
  2. 窗口位移：每次滑动多少个词

参数设置：窗口长度 = 4， 窗口位移 = 2

窗口位置 输入窗口内容 目标窗口内容
窗口1 [<BOS>, 机器, 学习, 是, 人工] [机器, 学习, 是, 人工, <EOS>]
窗口2 [<BOS>, 是, 人工, 智能, 的] [是, 人工, 智能, 的, <EOS>]
窗口3 [<BOS>, 智能, 的, 重要, 分支] [智能, 的, 重要, 分支, <EOS>]
... ... ...

2.3 损失函数：衡量"猜对"的程度

在训练过程中，我们需要一个标准来衡量AI"猜词"的水平。这就是损失函数 的作用。
计算原理：

  • 在每个位置，AI会给出对下一个词的"猜测"（一个概率分布）
  • 我们将这个猜测与真实的词比较
  • 计算它们之间的差异（使用交叉熵损失）

用数学公式表示：
L = − ∑ t = 1 T − 1 log ⁡ P ( x t + 1 ∣ x 1 , . . . , x t ) \mathcal{L} = -\sum_{t=1}^{T-1} \log P(x_{t+1} | x_1, ..., x_t) L=−t=1∑T−1logP(xt+1∣x1,...,xt)

当AI看到"机器学习是"时：

  • 它可能认为下一个是"人工智能"的概率是0.7
  • 是"深度学习"的概率是0.2
  • 是"一个"的概率是0.1

如果真实的下一个词是"人工智能"，那么损失就是：

  • 理想情况：AI应该100%确定是"人工智能"
  • 实际情况：AI只有70%确定
  • 损失值 = -log(0.7) ≈ 0.36

三、训练技巧：教师强制策略

3.1 教师强制（Teacher Forcing）的定义

教师强制是一种训练策略，在训练时总是使用真实的前一个词 作为当前步的输入，而不是使用模型自己可能错误的预测结果。

训练步骤 教师强制模式 自由运行模式
第一步 输入: [<BOS>] → 预测: "机器" 输入: [<BOS>] → 预测: "机器"
第二步 输入: [<BOS>, 机器] → 预测: "学习" 输入: [<BOS>, 预测1] → 预测: ?
第三步 输入: [<BOS>, 机器, 学习] → 预测: "是" 输入: [<BOS>, 预测1, 预测2] → 预测: ?
第四步 输入: [<BOS>, 机器, 学习, 是] → 预测: "人工" 输入: [<BOS>, 预测1, 预测2, 预测3] → 预测: ?

假设在自由运行模式下，模型在某个位置预测错误了：

教师强制模式（理想情况）：

python 复制代码 
步骤1: 输入[BOS] → 预测"机器" ✓
步骤2: 输入[BOS, 机器] → 预测"学习" ✓  
步骤3: 输入[BOS, 机器, 学习] → 预测"是" ✓
步骤4: 输入[BOS, 机器, 学习, 是] → 预测"人工" ✓
步骤5: 输入[BOS, 机器, 学习, 是, 人工] → 预测"智能" ✓
...
每一步都有正确的输入，能学到正确的关系

自由运行模式（假设步骤4预测错误）：

python 复制代码 
步骤1: 输入[BOS] → 预测"机器" ✓
步骤2: 输入[BOS, 机器] → 预测"学习" ✓
步骤3: 输入[BOS, 机器, 学习] → 预测"是" ✓
步骤4: 输入[BOS, 机器, 学习, 是] → 预测"技术" ✗（应该是"人工"）
步骤5: 输入[BOS, 机器, 学习, 是, 技术] → 预测"的" ✗（输入已经错了）
步骤6: 输入[BOS, 机器, 学习, 是, 技术, 的] → 预测"重要" ?（完全偏离了）
...
一个错误导致后续所有步骤都学不到正确关系

教师强制的优势

  1. 训练稳定：避免错误累积传播
  2. 收敛快速：每一步都有正确的"老师"指导
  3. 并行计算：可以同时计算所有位置的损失
  4. 梯度稳定：反向传播时梯度不会因错误预测而发散

3.2 暴露偏差问题与解决方法

暴露偏差 是教师强制策略的一个根本问题：训练时使用真实数据，但推理时使用模型自己的预测，导致输入分布不一致。

阶段 输入来源 输入质量 结果
训练时 使用训练集中的真实词 100%正确 模型在"理想条件"下学习
推理时 使用模型自己生成的词 可能包含错误 模型在"现实条件"下工作

例子说明：

训练时，模型学习的是：

  • 看到[<BOS>, 机器, 学习, 是] → 应该输出"人工"

但推理时，模型面对的是：

  • 看到[<BOS>, 机器, 学习, 是] → 输出"人工"（假设正确）
  • 下一步：看到[<BOS>, 机器, 学习, 是, 人工] → 输出"智能"
  • 再下一步：看到[<BOS>, 机器, 学习, 是, 人工, 智能] → 输出"的"

问题在于：如果模型在推理时某一步出错了（比如把"人工"输出成了"技术"），它从来没有在训练时见过"输入包含错误"的情况，不知道该如何处理。

解决方法

1. 计划采样（Scheduled Sampling）

这是一种折中方案：训练时不完全使用真实数据，也不完全使用模型预测，而是按一定概率混合 。在每个训练步骤，以概率ε使用真实的前一个词，以概率(1-ε)使用模型自己预测的词。
输入 t = { 真实词 t − 1 以概率 ϵ 预测词 t − 1 以概率 1 − ϵ \text{输入}t = \begin{cases} \text{真实词}{t-1} & \text{以概率 } \epsilon \\ \text{预测词}_{t-1} & \text{以概率 } 1-\epsilon \end{cases} 输入t={真实词t−1预测词t−1以概率 ϵ以概率 1−ϵ

训练过程：训练初期：ε接近1.0（几乎全用真实数据）；训练后期：ε逐渐减小（增加使用模型预测的比例）

2. 课程学习
  1. 第一阶段：完全使用教师强制，让模型先学会基本规律
  2. 第二阶段：逐渐引入模型自己的预测
  3. 第三阶段：完全或大部分使用模型预测
3. 波束搜索（推理时使用）

这不是训练技巧，而是推理时的补救措施：
普通贪婪解码：

复制代码 
看到"机器" → 选概率最高的"学习"
看到"机器学习" → 选概率最高的"是"
看到"机器学习是" → 选概率最高的"人工"
...

波束搜索（波束宽度=2）：通过保留多个候选序列，降低了单步错误导致全局失败的风险。

复制代码 
第一步：保留2个最可能的词 ["学习"(0.6), "技术"(0.3)]
第二步：对每个候选，扩展下一个词
  - "学习" + "是"(0.5) → 得分0.6×0.5=0.3
  - "学习" + "的"(0.2) → 得分0.6×0.2=0.12
  - "技术" + "是"(0.4) → 得分0.3×0.4=0.12
  - "技术" + "领域"(0.3) → 得分0.3×0.3=0.09
保留得分最高的2个序列 ["学习 是", "技术 是"]
第三步：继续扩展...

四、Transformer架构：自回归的引擎

4.1 后续掩码：因果关系的守护者

在自回归模型中，最核心的要求是：生成第t个词时，只能看到前面t-1个词，不能看到未来的词。这就是后续掩码（Causal Mask，也叫因果掩码）要确保的事情。

假设我们要生成机器学习是人工智能的重要分支这句话。在生成过程中：

  • 当AI生成第3个词"是"时，它只能看到[机器, 学习]
  • 当AI生成第5个词"智能"时，它只能看到[机器, 学习, 是, 人工]
  • 绝对不能让它看到"的"、"重要"、"分支"这些未来的词

但Transformer的注意力机制天生可以让每个位置看到所有位置。后续掩码就是在计算注意力时，用一个"眼罩"遮住未来的位置。

后续掩码是一个下三角矩阵 ，形状为[序列长度, 序列长度]。矩阵的每个位置M[i][j]表示：

  • 如果j ≤ i（当前位置i可以看位置j），则M[i][j] = 0
  • 如果j > i（当前位置i不能看未来的位置j），则M[i][j] = -∞

对于长度为4的序列，掩码矩阵为：

python 复制代码 
M = [[0, -∞, -∞, -∞],
     [0,  0, -∞, -∞],
     [0,  0,  0, -∞],
     [0,  0,  0,  0]]

注意力计算公式原本是：
Attention ( Q , K , V ) = softmax ( Q K T d k ) V \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V Attention(Q,K,V)=softmax(dk QKT)V

加入后续掩码后变成：
Attention ( Q , K , V ) = softmax ( Q K T d k + M ) V \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}} + M\right)V Attention(Q,K,V)=softmax(dk QKT+M)V

在PyTorch中，后续掩码的实现涉及特殊的梯度处理。我们来看一下具体细节：

python 复制代码 
import torch
import torch.nn.functional as F

def causal_attention(q, k, v):
    """带后续掩码的注意力计算"""
    # q, k, v的形状: [batch_size, seq_len, d_model]
    batch_size, seq_len, d_model = q.shape
    
    # 1. 计算注意力分数
    # scores形状: [batch_size, seq_len, seq_len]
    scores = torch.matmul(q, k.transpose(-2, -1)) / (d_model ** 0.5)
    
    # 2. 创建后续掩码（下三角矩阵）
    # 方法1：使用torch.tril
    mask = torch.tril(torch.ones(seq_len, seq_len))  # 下三角全1矩阵
    # 将1变成True（保留），0变成False（掩码）
    mask = mask.bool()
    
    # 3. 应用掩码
    # 将mask为False的位置（上三角）填充为非常大的负数
    # 这样在softmax中，这些位置的权重会变成0
    scores = scores.masked_fill(~mask, -1e9)
    
    # 4. 计算注意力权重
    attn_weights = F.softmax(scores, dim=-1)
    
    # 5. 加权求和
    output = torch.matmul(attn_weights, v)
    
    return output, attn_weights

梯度更新的特殊处理 ：

在PyTorch中，masked_fill操作和后续的梯度计算有一个关键特性：

  1. 掩码位置不参与梯度计算 ：

    当我们在scores上执行masked_fill(~mask, -1e9)时，被填充为-1e9的位置：

    • 在正向传播中，这些值被设为常数-1e9
    • 在反向传播中，这些常数位置的梯度为0

  2. softmax的数值稳定性：

    • 将未来位置设为-1e9，经过softmax后，这些位置的权重为：
      e − 1 e 9 e s 0 + e s 1 + . . . + e − 1 e 9 + . . . ≈ 0 \frac{e^{-1e9}}{e^{s_0} + e^{s_1} + ... + e^{-1e9} + ...} \approx 0 es0+es1+...+e−1e9+...e−1e9≈0
    • 由于数值下溢，实际上这些位置对输出没有任何贡献
    • 因此，这些位置在反向传播中也不会产生有效的梯度

  3. 梯度流向示意图：

    python 复制代码 
    正向传播：
位置0: 只计算基于位置0的梯度
位置1: 计算基于位置0、1的梯度
位置2: 计算基于位置0、1、2的梯度
...

反向传播：
位置2的梯度 ← 只能流向位置0、1、2的参数
位置1的梯度 ← 只能流向位置0、1的参数
位置0的梯度 ← 只能流向位置0的参数

nn.MultiheadAttention 是 PyTorch 提供的官方多头注意力实现，其内部已经优化了注意力计算。在自回归模型中，我们可以通过简单的方式实现因果掩码。

python 复制代码 
import torch
import torch.nn as nn

# 创建 MultiheadAttention
d_model = 512
n_heads = 8
mha = nn.MultiheadAttention(
    embed_dim=d_model,
    num_heads=n_heads,
    batch_first=True,  # 输入形状为 (batch, seq, feature)
    dropout=0.1
)

# 创建输入
batch_size = 2
seq_len = 10
x = torch.randn(batch_size, seq_len, d_model)

# 创建因果掩码
def create_causal_mask(seq_len, device):
    """创建因果掩码（上三角矩阵）"""
    # 上三角矩阵，对角线上方为True（需要屏蔽）
    mask = torch.triu(torch.ones(seq_len, seq_len, device=device), diagonal=1).bool()
    return mask

# 计算自注意力
causal_mask = create_causal_mask(seq_len, x.device)
output, attn_weights = mha(x, x, x, attn_mask=causal_mask)

4.2 位置编码：顺序的记忆

Transformer还有一个重要组件：位置编码。这是为了让模型知道词在序列中的位置。在传统的RNN中，词是一个接一个处理的，天然知道顺序。但Transformer是并行处理 所有词的，它本身不知道"机器"在第1位，"学习"在第2位。位置编码就是给每个位置一个独特的"位置指纹"。Transformer使用正弦和余弦函数来生成位置编码：

对于位置pos，维度i（从0到d/2-1）：
P E ( p o s , 2 i ) = sin ⁡ ( p o s 1000 0 2 i / d ) PE_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{2i/d}}\right) PE(pos,2i)=sin(100002i/dpos)
P E ( p o s , 2 i + 1 ) = cos ⁡ ( p o s 1000 0 2 i / d ) PE_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{2i/d}}\right) PE(pos,2i+1)=cos(100002i/dpos)

其中：

  • pos：词在序列中的位置（0, 1, 2, ...）
  • i：维度索引
  • d：模型的维度（如768）

每个词有两个部分的信息：

  1. 词嵌入：表示这个词本身的含义

  2. 位置编码：表示这个词在序列中的位置

    词嵌入(机器) + 位置编码(位置0) = 输入的"机器"
    词嵌入(学习) + 位置编码(位置1) = 输入的"学习"
    词嵌入(是) + 位置编码(位置2) = 输入的"是"
    ...

五、推理过程：从概率到文本

当AI模型训练完成后，我们需要让它生成文本 ，这就是推理过程。推理的本质是：模型基于已有的文本，预测下一个最可能的词，然后重复这个过程。

5.1 基础解码策略

贪婪解码：选择最确定的路

贪婪解码是最简单的策略：每一步都选择概率最高的词。

数学表达：
x t = arg ⁡ max ⁡ P ( x ∣ x 1 , . . . , x t − 1 ) x_t = \arg\max P(x | x_1, ..., x_{t-1}) xt=argmaxP(x∣x1,...,xt−1)

假设模型已经生成了"机器学习是"，现在要生成下一个词。模型给出的概率分布是：

  • "人工"：概率0.6
  • "深度"：概率0.3
  • "神经"：概率0.1

贪婪解码会选择概率最高的"人工"。

完整生成过程：

python 复制代码 
步骤1: 输入"机器" → 概率分布: 学习(0.7), 技术(0.2), 科学(0.1) → 选择"学习"
步骤2: 输入"机器学习" → 概率分布: 是(0.6), 的(0.3), 方法(0.1) → 选择"是"
步骤3: 输入"机器学习是" → 概率分布: 人工(0.6), 深度(0.3), 神经(0.1) → 选择"人工"
步骤4: 输入"机器学习是人工" → 概率分布: 智能(0.8), 智能的(0.1), 智能是(0.05) → 选择"智能"
...
最终: "机器学习是人工智能的重要分支"

优点 ：简单快速
缺点：可能错过更好的整体序列（因为每一步只考虑当前最优）

束搜索：保留多条候选路径

束搜索 维护k个最可能的序列，每一步扩展这些序列，然后保留概率最高的k个。维护Top-k序列： { ( s 1 , p 1 ) , ( s 2 , p 2 ) , . . . , ( s k , p k ) } \{(s_1, p_1), (s_2, p_2), ..., (s_k, p_k)\} {(s1,p1),(s2,p2),...,(sk,pk)}。假设我们要生成"机器学习是人工智能"，束搜索过程（束宽k=2）如下：

python 复制代码 
初始: 只有开始标记<BOS>

步骤1: 基于<BOS>生成第一个词
  候选1: "机器" (概率0.7)
  候选2: "计算" (概率0.2)
  候选3: "数据" (概率0.1)
  保留前2个: ["机器", "计算"]

步骤2: 扩展两个候选
  扩展"机器":
    "机器学习" (概率0.7 × 0.6 = 0.42)
    "机器技术" (概率0.7 × 0.3 = 0.21)
  扩展"计算":
    "计算科学" (概率0.2 × 0.5 = 0.10)
    "计算机" (概率0.2 × 0.4 = 0.08)
  合并后保留前2:
    "机器学习" (0.42)
    "机器技术" (0.21)

步骤3: 继续扩展
  扩展"机器学习":
    "机器学习是" (0.42 × 0.6 = 0.252)
    "机器学习在" (0.42 × 0.3 = 0.126)
  扩展"机器技术":
    "机器技术是" (0.21 × 0.4 = 0.084)
    "机器技术的" (0.21 × 0.5 = 0.105)
  保留前2:
    "机器学习是" (0.252)
    "机器学习在" (0.126)

继续这个过程，最终选择概率最高的完整序列。

优点 ：比贪婪解码找到更好序列的概率更高
缺点：计算量随束宽k线性增长

5.2 随机采样策略：增加多样性

随机采样不是每次都选概率最高的词，而是根据概率分布随机选择。这让生成更有创造性。

温度采样

温度采样 通过温度参数τ调整概率分布的"平滑度"：
P ′ ( x ) = exp ⁡ ( log ⁡ P ( x ) / τ ) ∑ x ′ exp ⁡ ( log ⁡ P ( x ′ ) / τ ) P'(x) = \frac{\exp(\log P(x) / \tau)}{\sum_{x'}\exp(\log P(x') / \tau)} P′(x)=∑x′exp(logP(x′)/τ)exp(logP(x)/τ)

其中τ是温度参数：

  • τ < 1：分布更尖锐（更确定，更少随机性）
  • τ = 1：原始分布
  • τ > 1：分布更平滑（更多随机性）

假设模型在某个位置给出的原始概率分布是：

  • "人工"：概率0.6
  • "深度"：概率0.3
  • "神经"：概率0.1
  1. 低温（τ=0.5，更确定）：
python 复制代码 
原始logits: log(0.6)=-0.51, log(0.3)=-1.20, log(0.1)=-2.30
除以τ: -0.51/0.5=-1.02, -1.20/0.5=-2.40, -2.30/0.5=-4.60
取exp: exp(-1.02)=0.36, exp(-2.40)=0.09, exp(-4.60)=0.01
归一化: "人工":0.36/(0.36+0.09+0.01)=0.78
        "深度":0.09/0.46=0.20
        "神经":0.01/0.46=0.02
结果：高概率词更高，低概率词更低
  1. 中温（τ=1.0，原始分布）：
python 复制代码 
保持原始概率："人工":0.6, "深度":0.3, "神经":0.1
  1. 高温（τ=2.0，更随机）：
python 复制代码 
除以τ: -0.51/2=-0.255, -1.20/2=-0.60, -2.30/2=-1.15
取exp: exp(-0.255)=0.77, exp(-0.60)=0.55, exp(-1.15)=0.32
归一化: "人工":0.77/(0.77+0.55+0.32)=0.47
        "深度":0.55/1.64=0.34
        "神经":0.32/1.64=0.19
结果：分布更均匀，低概率词概率提升

Top-k采样：限定候选池

Top-k采样：只从概率最高的k个词中随机选择。

例子（k=3）：

python 复制代码 
原始概率分布（前10个词）：
"人工":0.6, "深度":0.3, "神经":0.05, "机器":0.02, "计算":0.01, "算法":0.005, ...

Top-3候选："人工"(0.6), "深度"(0.3), "神经"(0.05)
重新归一化：总和=0.6+0.3+0.05=0.95
新分布："人工":0.6/0.95=0.63, "深度":0.3/0.95=0.32, "神经":0.05/0.95=0.05
从新分布中随机采样

Top-p采样（核采样）：按概率累积筛选

Top-p采样：从累积概率达到p的最小词集中采样。

python 复制代码 
按概率从高到低排序：
"人工":0.6, "深度":0.3, "神经":0.05, "机器":0.02, "计算":0.01, "算法":0.005,...

计算累积概率：
"人工":0.6
"人工"+"深度":0.9（达到p=0.9）
"人工"+"深度"+"神经":0.95（超过p=0.9）

取最小词集使累积概率≥0.9：{"人工", "深度"}
重新归一化：总和=0.6+0.3=0.9
新分布："人工":0.6/0.9=0.67, "深度":0.3/0.9=0.33
从新分布中随机采样

六、代码示例：手搓一个简单的 GPT

python 复制代码 
import random
import re
import warnings
from collections import Counter

import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.data import Dataset, DataLoader

warnings.filterwarnings('ignore')

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# ==================== 1. 设置和工具函数 ====================
SEED = 42
torch.manual_seed(SEED)
torch.cuda.manual_seed(SEED)
np.random.seed(SEED)
random.seed(SEED)
torch.backends.cudnn.deterministic = True

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(f"使用设备: {device}")

# 示例语料
corpus = [
    "机器学习是人工智能的重要分支，它使计算机能够从数据中学习。",
    "深度学习是机器学习的一个子集，使用神经网络来模拟人脑的工作方式。",
    "自然语言处理是人工智能的另一个重要领域，专注于计算机和人类语言之间的交互。",
    "Transformer模型在自然语言处理任务中表现出色，特别是在机器翻译和文本生成方面。",
    "自回归模型如GPT通过预测下一个词来生成连贯的文本。",
    "注意力机制是Transformer的核心，它允许模型在处理序列时关注不同部分的信息。",
    "预训练语言模型通过大规模无监督学习获得通用语言理解能力，然后可以通过微调适应特定任务。",
    "迁移学习使得我们可以在一个任务上学到的知识应用到另一个相关任务上，大大提高了模型效率。",
    "计算机视觉是人工智能的另一个重要分支，专注于让计算机理解和解释视觉信息。",
    "强化学习通过试错的方式让智能体学习如何在一系列动作中获得最大化的累积奖励。"
]


def clean_text(text):
    text = re.sub(r'[^\w\u4e00-\u9fa5，。！？；：,.!?;:\s]', '', text)
    text = re.sub(r'\s+', ' ', text)
    return text.strip()


def tokenize(text):
    tokens = []
    for char in text:
        if char.strip():
            tokens.append(char)
    return tokens


# ==================== 2. 数据预处理 ====================
cleaned_corpus = [clean_text(text) for text in corpus]
tokenized_corpus = [tokenize(text) for text in cleaned_corpus]

vocab_counter = Counter()
for tokens in tokenized_corpus:
    vocab_counter.update(tokens)

VOCAB_SIZE = 5000
special_tokens = ['<PAD>', '<UNK>', '<BOS>', '<EOS>']
vocab_items = special_tokens + [word for word, _ in vocab_counter.most_common(VOCAB_SIZE - len(special_tokens))]

word2idx = {word: idx for idx, word in enumerate(vocab_items)}
idx2word = {idx: word for idx, word in enumerate(vocab_items)}


# ==================== 3. Word2Vec词向量训练 ====================
class Word2VecEmbeddings:
    def __init__(self, tokenized_corpus, vector_size=128, window=5, min_count=1):
        self.tokenized_corpus = tokenized_corpus
        self.vector_size = vector_size
        self.window = window
        self.min_count = min_count
        self.model = None

    def train(self):
        # 在实际应用中，应该使用更大的语料训练Word2Vec
        # 这里为了简化，我们使用随机初始化
        self.model = type('obj', (object,), {'wv': {}})
        return self.model

    def get_embedding_matrix(self, word2idx):
        vocab_size = len(word2idx)
        embedding_matrix = np.random.randn(vocab_size, self.vector_size) * 0.1

        for word, idx in word2idx.items():
            if word in special_tokens:
                if word == '<PAD>':
                    embedding_matrix[idx] = np.zeros(self.vector_size)
                else:
                    embedding_matrix[idx] = np.random.randn(self.vector_size) * 0.01
            else:
                # 随机初始化非特殊标记
                embedding_matrix[idx] = np.random.randn(self.vector_size) * 0.1

        return torch.FloatTensor(embedding_matrix)


w2v = Word2VecEmbeddings(tokenized_corpus, vector_size=128)
embedding_matrix = w2v.get_embedding_matrix(word2idx)


# ==================== 4. 数据集和数据加载器 ====================
class TextDataset(Dataset):
    def __init__(self, tokenized_corpus, word2idx, max_len=100):
        self.tokenized_corpus = tokenized_corpus
        self.word2idx = word2idx
        self.max_len = max_len
        self.unk_idx = word2idx.get('<UNK>', 1)

    def __len__(self):
        return len(self.tokenized_corpus)

    def __getitem__(self, idx):
        tokens = self.tokenized_corpus[idx]
        tokens_with_special = ['<BOS>'] + tokens + ['<EOS>']

        if len(tokens_with_special) > self.max_len:
            tokens_with_special = tokens_with_special[:self.max_len]

        indices = [self.word2idx.get(token, self.unk_idx) for token in tokens_with_special]
        return torch.tensor(indices, dtype=torch.long)

    def collate_fn(self, batch):
        lengths = [len(seq) for seq in batch]
        max_len = max(lengths)

        padded_seqs = torch.full((len(batch), max_len), self.word2idx['<PAD>'], dtype=torch.long)

        for i, seq in enumerate(batch):
            seq_len = len(seq)
            padded_seqs[i, :seq_len] = seq

        # 创建padding掩码
        key_padding_mask = padded_seqs == self.word2idx['<PAD>']

        labels = padded_seqs.clone()

        for i in range(len(batch)):
            seq_len = lengths[i]
            if seq_len > 1:
                labels[i, :seq_len - 1] = padded_seqs[i, 1:seq_len]
                labels[i, seq_len - 1] = self.word2idx['<EOS>']
            else:
                labels[i, 0] = self.word2idx['<EOS>']

            labels[i, seq_len:] = -100

        return padded_seqs, key_padding_mask, labels, torch.tensor(lengths)


dataset = TextDataset(tokenized_corpus, word2idx, max_len=50)
dataloader = DataLoader(
    dataset,
    batch_size=2,
    shuffle=True,
    collate_fn=dataset.collate_fn
)


# ==================== 5. Transformer模型 ====================
class PositionalEncoding(nn.Module):
    def __init__(self, d_model, max_len=5000):
        super().__init__()
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-np.log(10000.0) / d_model))

        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)

        pe = pe.unsqueeze(0)
        self.register_buffer('pe', pe)

    def forward(self, x):
        return x + self.pe[:, :x.size(1)]


class TransformerBlock(nn.Module):
    def __init__(self, d_model, n_heads, d_ff, dropout=0.1):
        super().__init__()
        self.self_attn = nn.MultiheadAttention(d_model, n_heads, dropout=dropout, batch_first=True)
        self.feed_forward = nn.Sequential(
            nn.Linear(d_model, d_ff),
            nn.ReLU(),
            nn.Dropout(dropout),
            nn.Linear(d_ff, d_model)
        )
        self.norm1 = nn.LayerNorm(d_model)
        self.norm2 = nn.LayerNorm(d_model)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, attn_mask=None, key_padding_mask=None):
        attn_output, _ = self.self_attn(x, x, x, attn_mask=attn_mask, key_padding_mask=key_padding_mask)
        x = self.norm1(x + self.dropout(attn_output))
        ff_output = self.feed_forward(x)
        x = self.norm2(x + self.dropout(ff_output))
        return x


class AutoRegressiveTransformer(nn.Module):
    def __init__(self, vocab_size, d_model=128, n_heads=4, n_layers=4,
                 d_ff=512, max_len=100, dropout=0.1, embedding_matrix=None):
        super().__init__()
        self.vocab_size = vocab_size
        self.d_model = d_model
        self.n_heads = n_heads

        if embedding_matrix is not None:
            self.embedding = nn.Embedding.from_pretrained(embedding_matrix, freeze=False, padding_idx=0)
        else:
            self.embedding = nn.Embedding(vocab_size, d_model, padding_idx=0)

        self.positional_encoding = PositionalEncoding(d_model, max_len)
        self.transformer_layers = nn.ModuleList([
            TransformerBlock(d_model, n_heads, d_ff, dropout)
            for _ in range(n_layers)
        ])
        self.dropout = nn.Dropout(dropout)
        self.output_layer = nn.Linear(d_model, vocab_size)

        self._init_weights()

    def _init_weights(self):
        for p in self.parameters():
            if p.dim() > 1:
                nn.init.xavier_uniform_(p)

    def create_causal_mask(self, seq_len, device):
        mask = torch.triu(torch.ones(seq_len, seq_len, device=device), diagonal=1).bool()
        return mask

    def forward(self, input_ids, key_padding_mask=None, lengths=None):
        batch_size, seq_len = input_ids.shape
        device = input_ids.device

        x = self.embedding(input_ids)
        x = x * np.sqrt(self.d_model)
        x = self.positional_encoding(x)
        x = self.dropout(x)

        # 创建因果掩码
        causal_mask = self.create_causal_mask(seq_len, device)

        for layer in self.transformer_layers:
            x = layer(x, attn_mask=causal_mask, key_padding_mask=key_padding_mask)

        logits = self.output_layer(x)
        return logits

    def generate_with_visualization(self, prompt, max_len=50, temperature=1.0, top_k=None, top_p=None):
        """
        生成文本，并记录推理过程的详细信息
        返回生成的文本和推理步骤的详细信息
        """
        self.eval()
        device = next(self.parameters()).device

        tokens = tokenize(clean_text(prompt))
        indices = [word2idx.get('<BOS>', 2)] + [word2idx.get(token, 1) for token in tokens]

        # 记录每一步的推理信息
        inference_steps = []

        with torch.no_grad():
            for step in range(max_len):
                input_tensor = torch.tensor([indices], device=device)
                logits = self.forward(input_tensor)
                last_logits = logits[0, -1, :]

                if temperature != 1.0:
                    last_logits = last_logits / temperature

                probs = F.softmax(last_logits, dim=-1)

                # 记录原始概率分布
                original_probs = probs.clone()

                # 采样策略
                if top_k is not None:
                    top_k_probs, top_k_indices = torch.topk(probs, min(top_k, len(probs)))
                    probs = torch.zeros_like(probs)
                    probs[top_k_indices] = top_k_probs
                    probs = probs / probs.sum()

                if top_p is not None and top_p < 1.0:
                    sorted_probs, sorted_indices = torch.sort(probs, descending=True)
                    cumulative_probs = torch.cumsum(sorted_probs, dim=-1)
                    sorted_indices_to_remove = cumulative_probs > top_p
                    if sorted_indices_to_remove[0]:
                        sorted_indices_to_remove[0] = False
                    indices_to_remove = sorted_indices[sorted_indices_to_remove]
                    probs[indices_to_remove] = 0
                    probs = probs / probs.sum()

                # 从分布中采样
                next_idx = torch.multinomial(probs, 1).item()

                # 记录这一步的详细信息
                current_input = ''.join([idx2word.get(idx, '<UNK>') for idx in indices[1:]])  # 跳过BOS
                selected_token = idx2word.get(next_idx, '<UNK>')
                selected_prob = probs[next_idx].item()

                # 获取前3个最可能的候选词（使用原始概率）
                topk_values, topk_indices = torch.topk(original_probs, min(3, len(original_probs)))  # 修改为3
                candidates = [idx2word.get(idx.item(), '<UNK>') for idx in topk_indices]
                candidate_probs = topk_values.cpu().numpy()  # 转换为numpy用于记录

                inference_steps.append({
                    'step': step + 1,
                    'current_input': current_input,
                    'candidates': candidates,
                    'candidate_probs': candidate_probs,
                    'selected_token': selected_token,
                    'selected_prob': selected_prob
                })

                # 添加到序列
                indices.append(next_idx)

                # 如果生成了结束标记，停止
                if idx2word.get(next_idx, '<UNK>') == '<EOS>':
                    break

        generated_tokens = []
        for idx in indices[1:]:  # 跳过BOS
            token = idx2word.get(idx, '<UNK>')
            if token == '<EOS>':
                break
            generated_tokens.append(token)

        generated_text = ''.join(generated_tokens)
        return generated_text, inference_steps

    def generate(self, prompt, max_len=50, temperature=1.0, top_k=None, top_p=None):
        """普通生成函数，不记录详细信息"""
        generated_text, _ = self.generate_with_visualization(
            prompt, max_len, temperature, top_k, top_p
        )
        return generated_text


# ==================== 6. 训练函数 ====================
def train_epoch(model, dataloader, criterion, optimizer, device, clip=1.0):
    model.train()
    total_loss = 0
    total_tokens = 0

    for batch_idx, (inputs, key_padding_mask, labels, lengths) in enumerate(dataloader):
        inputs = inputs.to(device)
        key_padding_mask = key_padding_mask.to(device)
        labels = labels.to(device)

        logits = model(inputs, key_padding_mask, lengths)
        loss = criterion(logits.view(-1, model.vocab_size), labels.view(-1))

        optimizer.zero_grad()
        loss.backward()
        torch.nn.utils.clip_grad_norm_(model.parameters(), clip)
        optimizer.step()

        num_tokens = (labels != -100).sum().item()
        total_loss += loss.item() * num_tokens
        total_tokens += num_tokens

    avg_loss = total_loss / total_tokens if total_tokens > 0 else 0
    return avg_loss


def evaluate(model, dataloader, criterion, device):
    model.eval()
    total_loss = 0
    total_tokens = 0

    with torch.no_grad():
        for inputs, key_padding_mask, labels, lengths in dataloader:
            inputs = inputs.to(device)
            key_padding_mask = key_padding_mask.to(device)
            labels = labels.to(device)

            logits = model(inputs, key_padding_mask, lengths)
            loss = criterion(logits.view(-1, model.vocab_size), labels.view(-1))

            num_tokens = (labels != -100).sum().item()
            total_loss += loss.item() * num_tokens
            total_tokens += num_tokens

    avg_loss = total_loss / total_tokens if total_tokens > 0 else 0
    perplexity = np.exp(avg_loss)
    return avg_loss, perplexity


# ==================== 7. 可视化函数 ====================
def visualize_inference_steps(inference_steps, prompt, save_path="inference_visualization.png"):
    """
    可视化推理过程的每一步
    """
    if not inference_steps:
        print("没有推理步骤可可视化")
        return

    # 限制最多显示10步
    display_steps = inference_steps[:8]  # 只取前10步

    # 计算需要多少个子图
    n_steps = len(display_steps)
    n_cols = 4
    n_rows = (n_steps + 1) // n_cols

    fig, axes = plt.subplots(n_rows, n_cols, figsize=(15, 5 * n_rows))
    if n_steps == 1:
        axes = np.array([[axes]])
    elif n_rows == 1:
        axes = axes.reshape(1, -1)
    elif n_cols == 1:
        axes = axes.reshape(-1, 1)

    fig.suptitle(f"推理过程可视化 - 提示: '{prompt}' (显示前{min(9, len(inference_steps))}步)", fontsize=16, y=1.02)

    for i, step_info in enumerate(display_steps):
        row = i // n_cols
        col = i % n_cols
        ax = axes[row, col]

        candidates = step_info['candidates'][:3]  # 只取前3个候选词
        probs = step_info['candidate_probs'][:3]  # 只取前3个概率
        selected_token = step_info['selected_token']
        selected_prob = step_info['selected_prob']
        current_input = step_info['current_input']

        # 如果当前输入太长，截断显示
        if len(current_input) > 20:
            current_input = current_input[:20] + "..."

        # 为被选中的token设置不同的颜色
        colors = ['lightblue'] * len(candidates)
        for j, cand in enumerate(candidates):
            if cand == selected_token:
                colors[j] = 'red'
                break

        # 绘制柱状图
        bars = ax.bar(range(len(candidates)), probs, color=colors, edgecolor='black')
        ax.set_xticks(range(len(candidates)))
        ax.set_xticklabels(candidates, rotation=45, ha='right', fontsize=8)
        ax.set_ylabel('概率')
        ax.set_ylim([0, max(probs) * 1.2 if len(probs) > 0 else 1.0])

        # 添加概率值标签
        for j, (bar, prob) in enumerate(zip(bars, probs)):
            height = bar.get_height()
            ax.text(bar.get_x() + bar.get_width() / 2., height + 0.001,
                    f'{prob:.3f}', ha='center', va='bottom', fontsize=7, rotation=90)

        # 设置标题
        title = f"步骤 {step_info['step']}: 已生成 '{current_input}'"
        title += f"\n选中: '{selected_token}' (概率: {selected_prob:.3f})"
        ax.set_title(title, fontsize=10)

        # 添加网格
        ax.yaxis.grid(True, linestyle='--', alpha=0.7)

    # 隐藏多余的子图
    for i in range(n_steps, n_rows * n_cols):
        row = i // n_cols
        col = i % n_cols
        axes[row, col].axis('off')

    plt.tight_layout()
    plt.savefig(save_path, dpi=150, bbox_inches='tight')
    plt.show()
    print(f"可视化已保存到: {save_path}")


def train_model():
    VOCAB_SIZE = len(word2idx)
    D_MODEL = 128
    N_HEADS = 4
    N_LAYERS = 4
    D_FF = 512
    MAX_LEN = 50
    DROPOUT = 0.1

    model = AutoRegressiveTransformer(
        vocab_size=VOCAB_SIZE,
        d_model=D_MODEL,
        n_heads=N_HEADS,
        n_layers=N_LAYERS,
        d_ff=D_FF,
        max_len=MAX_LEN,
        dropout=DROPOUT,
        embedding_matrix=embedding_matrix
    ).to(device)

    criterion = nn.CrossEntropyLoss(ignore_index=-100)
    optimizer = optim.Adam(model.parameters(), lr=0.001, betas=(0.9, 0.98), eps=1e-9)
    scheduler = optim.lr_scheduler.StepLR(optimizer, step_size=5, gamma=0.5)

    num_epochs = 20

    for epoch in range(num_epochs):
        train_loss = train_epoch(model, dataloader, criterion, optimizer, device)
        val_loss, perplexity = evaluate(model, dataloader, criterion, device)
        scheduler.step()

    return model


# ==================== 9. 推理示例 ====================
def inference_examples(model):
    test_prompts = ["机器学习", "人工智能", "深度学习模型", "人工智能技术"]
    strategies = [
        ("贪婪解码", {"temperature": 0.1, "top_k": None, "top_p": None}),
        ("温度采样(τ=0.8)", {"temperature": 0.8, "top_k": None, "top_p": None}),
        ("温度采样(τ=1.2)", {"temperature": 1.2, "top_k": None, "top_p": None}),
        ("Top-k采样(k=10)", {"temperature": 1.0, "top_k": 10, "top_p": None}),
        ("Top-p采样(p=0.9)", {"temperature": 1.0, "top_k": None, "top_p": 0.9}),
    ]

    print("\n" + "=" * 60)
    print("推理示例:")
    print("=" * 60)

    for prompt in test_prompts:
        print(f"\n提示: '{prompt}'")
        for strategy_name, params in strategies:
            generated = model.generate(prompt, max_len=30, **params)
            print(f"  {strategy_name}: {generated}")
        print("-" * 40)


# ==================== 10. 详细推理过程 ====================
def detailed_inference_visualization(model, prompt="机器学习", strategy_name="贪婪解码",
                                     temperature=0.1, top_k=None, top_p=None, max_steps=10):  # 修改为10步
    """
    执行详细的推理过程并可视化
    """
    print(f"\n{'=' * 60}")
    print(f"详细推理过程: 提示='{prompt}', 策略={strategy_name}")
    print(f"{'=' * 60}")

    # 使用可视化生成函数
    generated_text, inference_steps = model.generate_with_visualization(
        prompt, max_len=max_steps, temperature=temperature, top_k=top_k, top_p=top_p
    )

    print(f"生成结果: {generated_text}")
    print(f"\n推理步骤详情 (显示前{min(10, len(inference_steps))}步):")

    for step in inference_steps[:10]:  # 只显示前10步
        print(f"\n步骤 {step['step']}:")
        print(f"  当前输入: '{step['current_input']}'")
        print(f"  候选词 (前3个):")
        for cand, prob in zip(step['candidates'][:3], step['candidate_probs'][:3]):  # 只显示前3个
            marker = " ✓" if cand == step['selected_token'] else ""
            print(f"    '{cand}': {prob:.4f}{marker}")
        print(f"  选中: '{step['selected_token']}' (概率: {step['selected_prob']:.4f})")

    # 可视化
    if inference_steps:
        save_path = f"inference_{prompt}_{strategy_name}.png"
        visualize_inference_steps(inference_steps, prompt, save_path)


if __name__ == "__main__":
    model = train_model()
    inference_examples(model)
    detailed_inference_visualization(
        model,
        prompt="人工智能",
        strategy_name="温度采样",
        temperature=0.8,
        max_steps=10
    )

    print("\n模型训练和推理完成！")
python 复制代码 
提示: '机器学习'
  贪婪解码: 机器学习是人工智能的重要分支，它使计算机能够从数据中学习。
  温度采样(τ=0.8): 机器学习是人工智能的另一个重要分支，它使计算机中学习获得最大通过测任
  温度采样(τ=1.2): 机器学习是人工<BOS>能使获得们可和以个奖它错动别是在核心解人工。
  Top-k采样(k=10): 机器学习是人工智能的重要分支，它使计算机能型理解中学习。
  Top-p采样(p=0.9): 机器学习是人工智能的另一个重要领域，专注于让计算机能体学习。
----------------------------------------

提示: '人工智能'
  贪婪解码: 人工智能的重要分支，它使计算机能体学习获得最大化的文本。
  温度采样(τ=0.8): 人工智能专注意力模型使贯的信算机能的相关任务中表现出色，它拟通过相关
  温度采样(τ=1.2): 人工智能移子过大言另一
  Top-k采样(k=10): 人工智能的知效率智能体学习通过大规f到的核心，特定学习是人类语言模型
  Top-p采样(p=0.9): 人工智能的方式让智能的移s序列成连注于让何在一个关任务特互。
----------------------------------------

提示: '深度学习模型'
  贪婪解码: 深度学习模型在一个任务上学习的另一个任务中表现出色，专注于计算机器翻译和
  温度采样(τ=0.8): 深度学习模型在处们可以在一个子集，释络来注于关注于计算机何在一个重要间的
  温度采样(τ=1.2): 深度学习模型Po注于forme域a语言拟人中nm任务子络网人脑的G支<UNK>。
  Top-k采样(k=10): 深度学习模型效分的一个言分支，它使计算机器学习获得我们可以作er的交下个
  Top-p采样(p=0.9): 深度学习模型理络提的分练个子一个学习<PAD>能的文本到的方式。
----------------------------------------

提示: '人工智能技术'
  贪婪解码: 人工智能<UNK><UNK>ransformermer模型在机器学习。
  温度采样(τ=0.8): 人工智能<UNK><UNK>习获得通过大强个重要领域应在一系列动作中学习获得过微调适应知
  温度采样(τ=1.2): 人工智能<UNK><UNK>关我们重特器之成类别言之间的可获得最预允经专不同
  Top-k采样(k=10): 人工智能<UNK><UNK>Transformer模型在处理解和文本。
  Top-p采样(p=0.9): 人工智能<UNK><UNK>得我T练语言度了模型在处理解和文本大规视觉部是人脑部信息。
----------------------------------------

============================================================
详细推理过程: 提示='人工智能', 策略=温度采样
============================================================
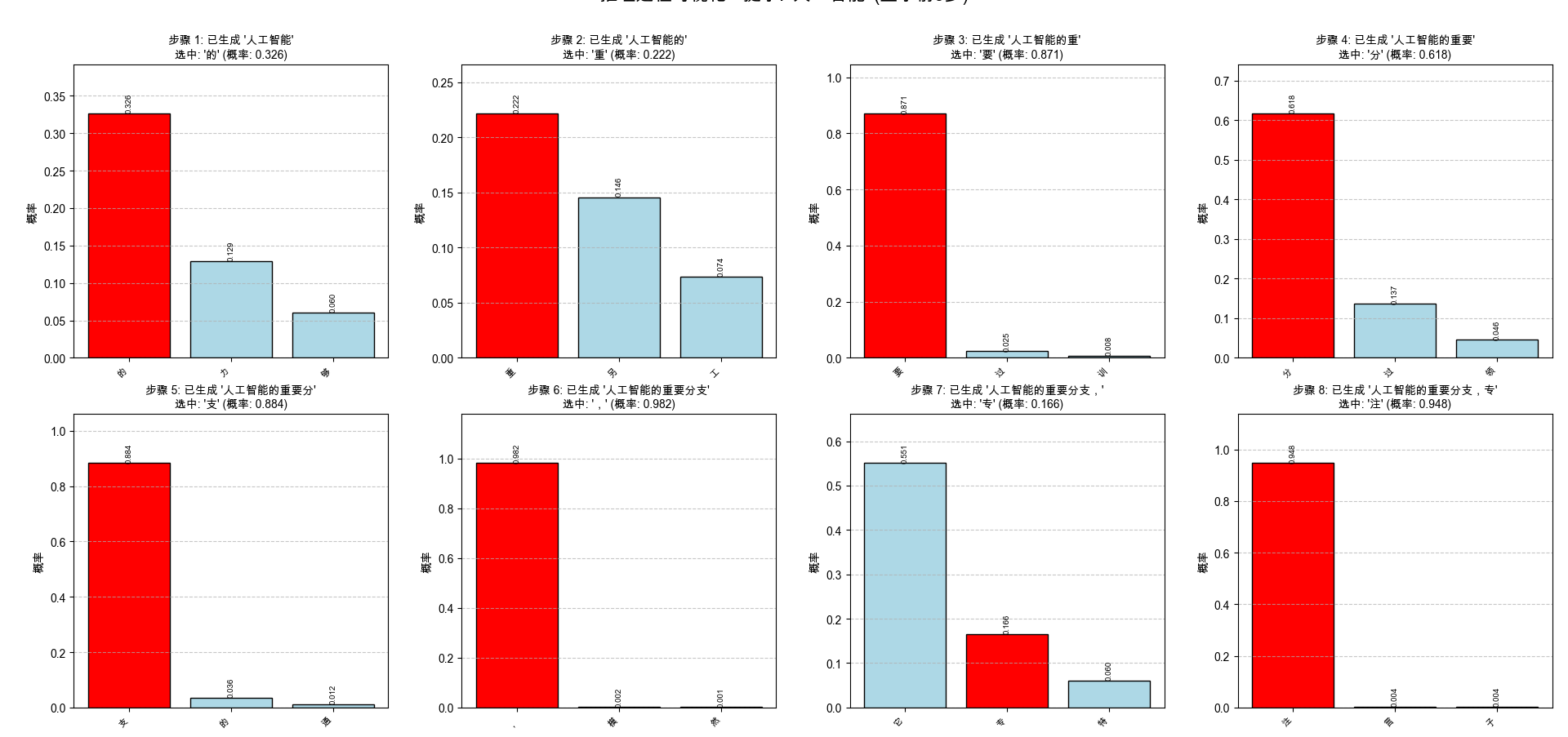
生成结果: 人工智能的重要分支，专注于让

推理步骤详情 (显示前10步):

步骤 1:
  当前输入: '人工智能'
  候选词 (前3个):
    '的': 0.3264 ✓
    '力': 0.1290
    '够': 0.0600
  选中: '的' (概率: 0.3264)

步骤 2:
  当前输入: '人工智能的'
  候选词 (前3个):
    '重': 0.2218 ✓
    '另': 0.1457
    '工': 0.0736
  选中: '重' (概率: 0.2218)

步骤 3:
  当前输入: '人工智能的重'
  候选词 (前3个):
    '要': 0.8711 ✓
    '过': 0.0248
    '训': 0.0077
  选中: '要' (概率: 0.8711)

步骤 4:
  当前输入: '人工智能的重要'
  候选词 (前3个):
    '分': 0.6177 ✓
    '过': 0.1368
    '领': 0.0459
  选中: '分' (概率: 0.6177)

步骤 5:
  当前输入: '人工智能的重要分'
  候选词 (前3个):
    '支': 0.8837 ✓
    '的': 0.0361
    '通': 0.0123
  选中: '支' (概率: 0.8837)

步骤 6:
  当前输入: '人工智能的重要分支'
  候选词 (前3个):
    '，': 0.9817 ✓
    '模': 0.0023
    '然': 0.0014
  选中: '，' (概率: 0.9817)

步骤 7:
  当前输入: '人工智能的重要分支，'
  候选词 (前3个):
    '它': 0.5508
    '专': 0.1657 ✓
    '特': 0.0605
  选中: '专' (概率: 0.1657)

步骤 8:
  当前输入: '人工智能的重要分支，专'
  候选词 (前3个):
    '注': 0.9476 ✓
    '言': 0.0038
    '子': 0.0036
  选中: '注' (概率: 0.9476)

步骤 9:
  当前输入: '人工智能的重要分支，专注'
  候选词 (前3个):
    '于': 0.8476 ✓
    '意': 0.0239
    '不': 0.0134
  选中: '于' (概率: 0.8476)

步骤 10:
  当前输入: '人工智能的重要分支，专注于'
  候选词 (前3个):
    '计': 0.3456
    '让': 0.2211 ✓
    '模': 0.0449
  选中: '让' (概率: 0.2211)

当输入prompt为"人工智能技术"时，模型将"技术"编码为连续的"<UNK>"，导致生成质量严重下降。

根本原因：

  1. 训练数据太小（仅10个句子），词汇表只包含训练数据中出现过的字符
  2. "技"和"术"两个字从未在训练数据中出现，因此不在词汇表。
  3. 推理时，不在词汇表中的字符被编码为""
  4. 结果影响：模型看到"<UNK>"后失去有效上下文- 生成内容变得不合理甚至包含乱码- 一旦开始生成""，容易陷入恶性循环。

解决方案：

  1. 扩大训练数据，增加词汇覆盖
  2. 推理时屏蔽"<UNK>"的概率
  3. 使用更好的分词策略

本代码实现了一个完整的自回归Transformer语言模型，核心功能包括：

  1. 数据预处理：中文文本清洗、分词、词汇表构建
  2. 词向量训练：Word2Vec预训练词向量初始化
  3. 模型架构：完整的Transformer解码器
  4. 训练过程：自回归语言模型训练
  5. 推理生成：多种采样策略生成文本
  6. 可视化：推理过程的详细可视化

这个代码展示了自回归Transformer语言模型的完整实现，从数据预处理到模型训练，再到多种推理策略和可视化。虽然模型规模较小，但包含了GPT等大语言模型的核心原理：

  1. 自回归：逐词生成，每个词基于前面所有词
  2. Transformer架构：多头注意力、前馈网络、残差连接
  3. 多种采样策略：平衡生成质量与多样性
  4. 训练-推理一致性：训练时的右移策略与推理时的生成过程一致
相关推荐
Java后端的Ai之路7 小时前
【分析式AI】-分类与回归的区别以及内联
人工智能·分类·数据挖掘·回归·aigc
亿坊电商7 小时前
跨境出口电商系统如何提升出口电商业务的效率和可管理性？
数据挖掘·数据分析·系统架构
六行神算API-天璇8 小时前
技术实践：用大模型平台重构医疗数据分析Pipeline
人工智能·重构·数据挖掘·数据分析
大千AI助手8 小时前
GPT-Neo：开源大型自回归语言模型的实现与影响
人工智能·gpt·机器学习·开源·大模型·大千ai助手·gpt-neo
桂花饼8 小时前
[首发实测] GPT-5.2 pro 接入指南：SWE-bench 80% 胜率的“工程级”模型，Python 如何实现低成本调用？
python·gpt·ai编程·大模型实战·gemini 3 pro·claude opus 4.5
AAD555888999 小时前
轴体分类识别：基于Decoupled-Solo-Light模型的中心轴、铁质轴和尼龙轴自动检测与分类系统
人工智能·分类·数据挖掘
子夜江寒9 小时前
数据处理：下采样与SMOTE过采样
回归
Dekesas96959 小时前
基于YOLO11-seg的白蚁种类智能识别与分类系统——利用深度学习技术实现白蚁图像分割与多类别精准识别
深度学习·数据挖掘
albert-einstein10 小时前
JBoss 4.x JBossMQ JMS 反序列化漏洞 CVE-2017-7504(参考peiqi文库以及gpt)
gpt
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04【AutoGLM部署】本地私有化部署AI手机Agent05Open-AutoGLM Windows 安装部署教程06Cursor 又偷偷更新，这个功能太实用：Visual Editor for Cursor Browser07在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）08【超详细教程】手把手教你从微软官网免费下载Windows 10官方原版ISO镜像（2025最新版）09安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）10BongoCat - 跨平台键盘猫动画工具