从零构建一个多目标多传感器融合跟踪器 多目标多传感器融合跟踪算法原理
在当今的科技领域,多目标多传感器融合跟踪技术应用广泛,从智能交通中的车辆行人跟踪,到军事领域的目标监测等都离不开它。今天咱们就来聊聊如何从零构建这样一个跟踪器,顺便深入探究下相关算法原理。
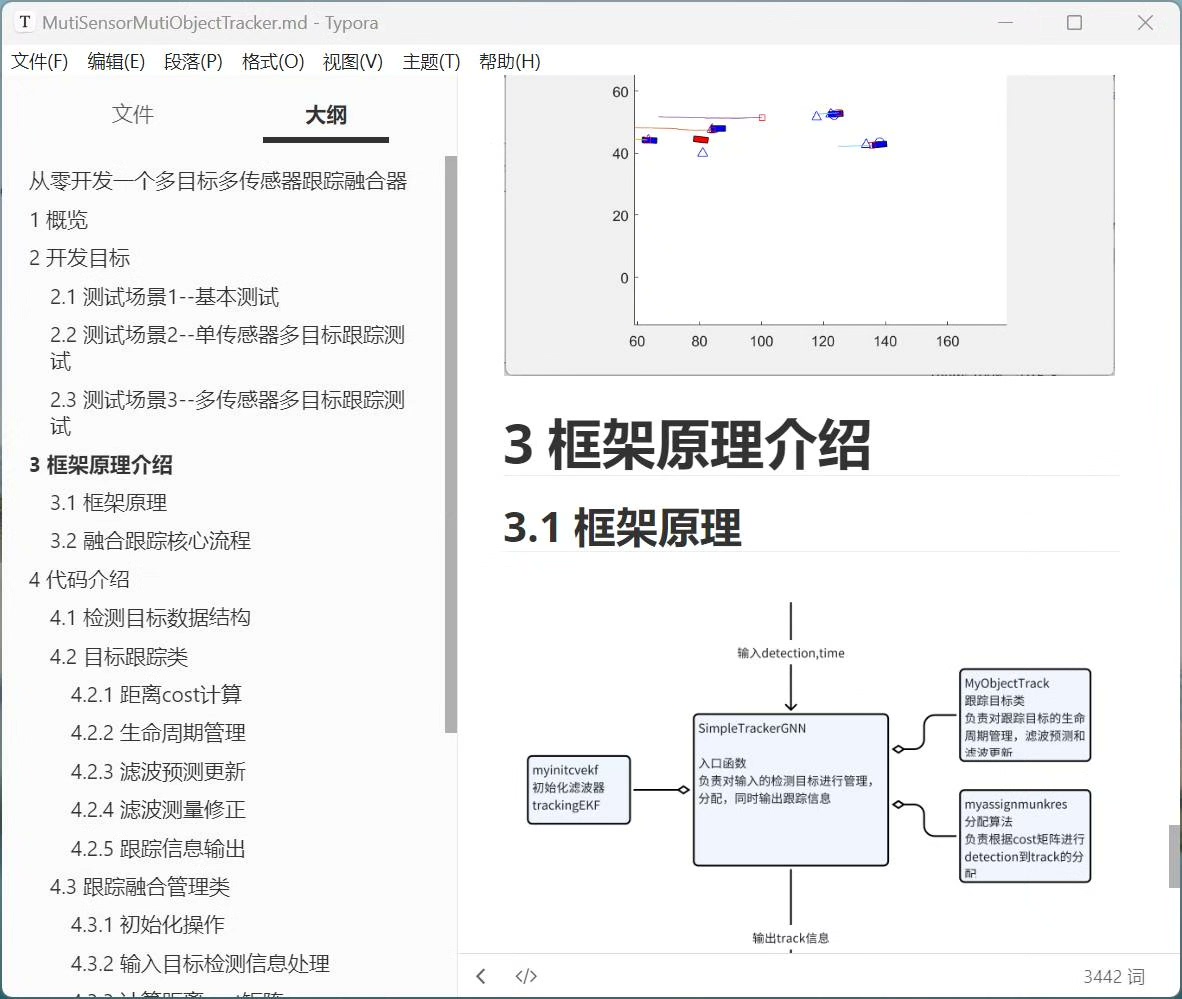
多目标多传感器融合跟踪算法原理
数据关联
在多目标跟踪里,数据关联是个关键环节。简单说,就是要把不同传感器在不同时刻收集到的数据,正确地对应到实际场景中的各个目标。比如有两个摄像头同时监测一个广场,一个摄像头在某时刻检测到一个物体,另一个摄像头也检测到物体,我们要判断这两个检测是不是对应同一个目标。
假设有一个简单的场景,有两个传感器,传感器1检测到目标位置列表 det1 = [(10, 20), (30, 40)],传感器2检测到 det2 = [(12, 22), (32, 42)]。这里数据关联就是要找到最合理的对应关系。一种简单的方法是计算距离,比如欧氏距离。
python
import math
def euclidean_distance(point1, point2):
return math.sqrt((point1[0] - point2[0])**2 + (point1[1] - point2[1])**2)
det1 = [(10, 20), (30, 40)]
det2 = [(12, 22), (32, 42)]
for i in range(len(det1)):
for j in range(len(det2)):
dist = euclidean_distance(det1[i], det2[j])
print(f"距离 between det1[{i}] and det2[{j}] is {dist}")上述代码通过计算不同检测点之间的欧氏距离,帮助我们直观地了解各个检测数据间的相似程度,从而辅助数据关联决策。但实际场景要复杂得多,会有遮挡、噪声等干扰,所以还会用到更高级的算法,比如匈牙利算法,它能有效解决二分图最大匹配问题,从而更好地完成数据关联。
状态估计
状态估计就是根据传感器收集的数据,推测目标的实际状态,像位置、速度等。常见的方法是卡尔曼滤波。卡尔曼滤波基于线性系统状态空间模型,它分为预测和更新两个步骤。
预测步骤:
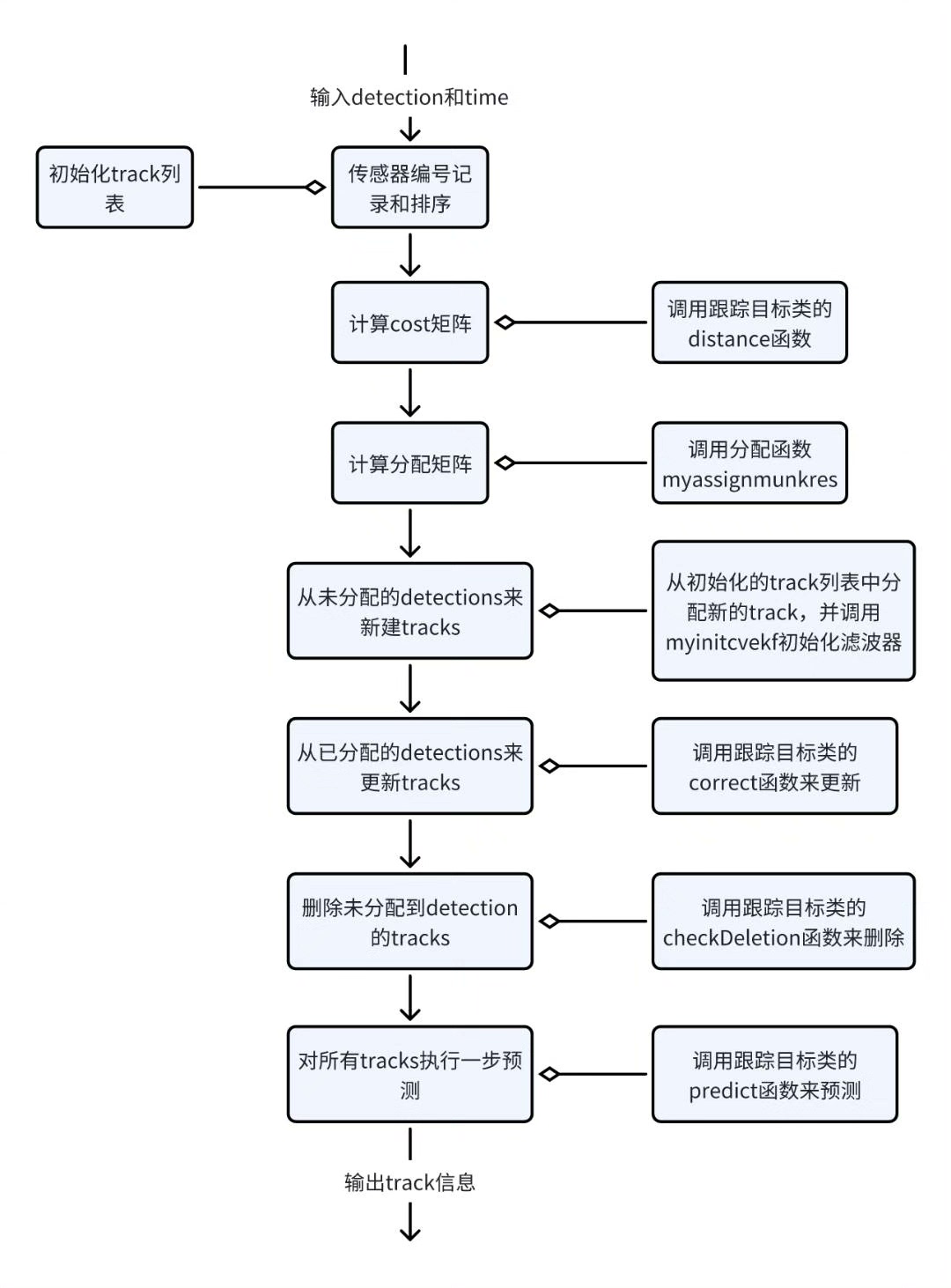
\[ \hat{X}{k|k - 1} = A\hat{X}{k - 1|k - 1} + Bu_{k} \]
\[ P*{k|k - 1} = AP*{k - 1|k - 1}A^{T}+Q \]
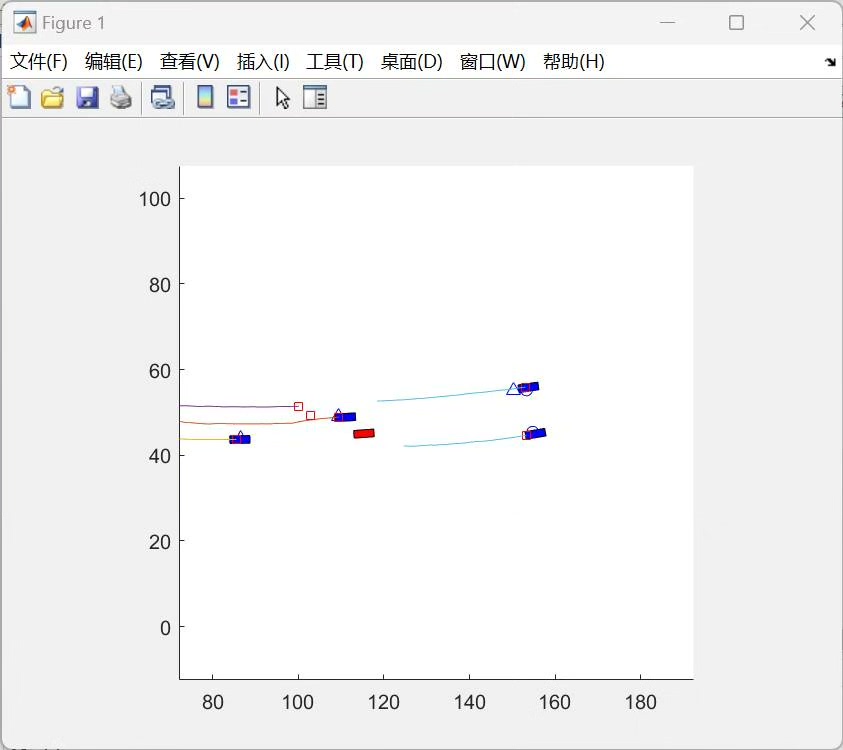
这里 \(\hat{X}{k|k - 1}\) 是基于上一时刻估计的当前时刻状态预测值,\(A\) 是状态转移矩阵,\(u{k}\) 是控制量,\(P_{k|k - 1}\) 是预测协方差,\(Q\) 是过程噪声协方差。
更新步骤:
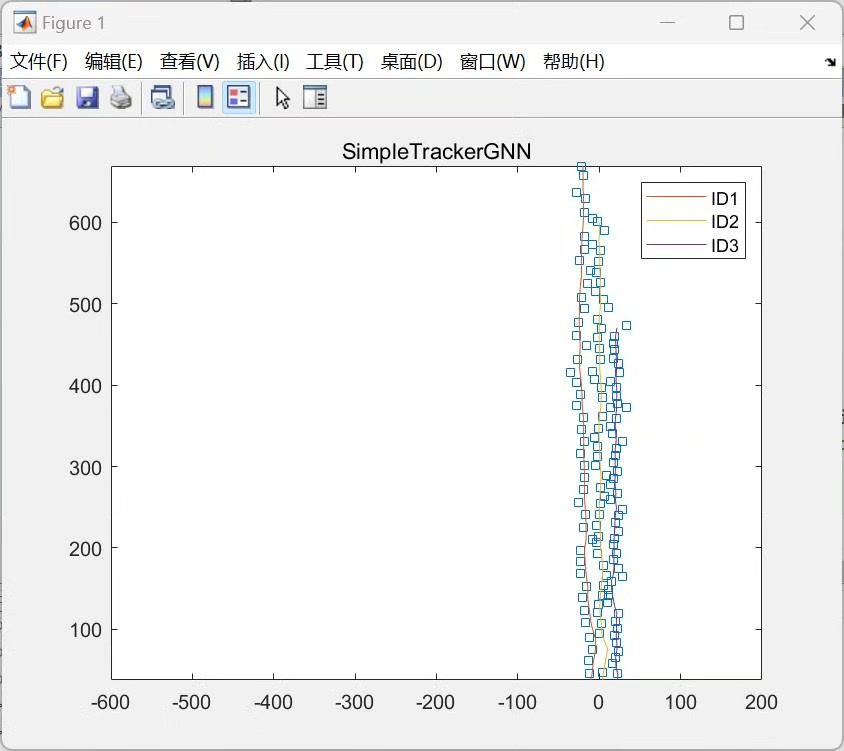
\[ K*{k} = P*{k|k - 1}H^{T}(HP_{k|k - 1}H^{T}+R)^{-1} \]
\[ \hat{X}{k|k} = \hat{X} {k|k - 1}+K*{k}(Z*{k}-H\hat{X}_{k|k - 1}) \]
\[ P*{k|k} = (I - K*{k}H)P_{k|k - 1} \]
\(K*{k}\) 是卡尔曼增益,\(H\) 是观测矩阵,\(Z*{k}\) 是观测值,\(R\) 是观测噪声协方差。
下面是一个简单的卡尔曼滤波Python实现:
python
import numpy as np
class KalmanFilter:
def __init__(self, dt, u_x, u_y, std_acc, x_std_meas, y_std_meas):
# dt 时间间隔,u_x, u_y 控制量,std_acc 加速度噪声,x_std_meas, y_std_meas 测量噪声
self.dt = dt
self.u = np.matrix([[u_x], [u_y]])
self.x = np.matrix([[0], [0], [0], [0]])
self.P = np.eye(4)
self.Q = np.matrix([[(self.dt**4)/4*std_acc**2, 0, (self.dt**3)/2*std_acc**2, 0],
[0, (self.dt**4)/4*std_acc**2, 0, (self.dt**3)/2*std_acc**2],
[(self.dt**3)/2*std_acc**2, 0, (self.dt**2)*std_acc**2, 0],
[0, (self.dt**3)/2*std_acc**2, 0, (self.dt**2)*std_acc**2]])
self.R = np.matrix([[x_std_meas**2, 0],
[0, y_std_meas**2]])
self.A = np.matrix([[1, 0, self.dt, 0],
[0, 1, 0, self.dt],
[0, 0, 1, 0],
[0, 0, 0, 1]])
self.H = np.matrix([[1, 0, 0, 0],
[0, 1, 0, 0]])
def predict(self):
self.x = np.dot(self.A, self.x) + self.u
self.P = np.dot(np.dot(self.A, self.P), self.A.T) + self.Q
return self.x
def update(self, z):
y = z - np.dot(self.H, self.x)
S = self.R + np.dot(self.H, np.dot(self.P, self.H.T))
K = np.dot(np.dot(self.P, self.H.T), np.linalg.inv(S))
self.x = self.x + np.dot(K, y)
I = np.eye(self.x.shape[0])
self.P = (I - np.dot(K, self.H)) * self.P
return self.x这段代码实现了一个基本的二维卡尔曼滤波器,能根据给定的参数对目标状态进行预测和更新。
从零构建跟踪器
初始化
首先要初始化跟踪器的参数,像传感器的参数(例如分辨率、测量范围等),以及跟踪算法所需的参数(如卡尔曼滤波的噪声参数)。
python
# 初始化传感器参数
sensor1_params = {
"resolution": (640, 480),
"range": 100
}
# 初始化卡尔曼滤波参数
dt = 0.1
u_x = 0
u_y = 0
std_acc = 1
x_std_meas = 0.1
y_std_meas = 0.1
kf = KalmanFilter(dt, u_x, u_y, std_acc, x_std_meas, y_std_meas)数据采集与预处理
从各个传感器采集数据后,要进行预处理。比如图像传感器采集的图像可能要进行去噪、目标检测等操作。假设我们用OpenCV进行目标检测:
python
import cv2
# 加载预训练模型
net = cv2.dnn.readNetFromCaffe('deploy.prototxt', 'weights.caffemodel')
def detect_objects(frame):
(h, w) = frame.shape[:2]
blob = cv2.dnn.blobFromImage(cv2.resize(frame, (300, 300)), 0.007843, (300, 300), 127.5)
net.setInput(blob)
detections = net.forward()
detected_objects = []
for i in range(0, detections.shape[2]):
confidence = detections[0, 0, i, 2]
if confidence > 0.5:
idx = int(detections[0, 0, i, 1])
box = detections[0, 0, i, 3:7] * np.array([w, h, w, h])
(startX, startY, endX, endY) = box.astype("int")
detected_objects.append((startX, startY, endX, endY))
return detected_objects这段代码利用预训练的Caffe模型对输入图像进行目标检测,返回检测到的目标位置。
融合与跟踪
将预处理后的数据进行融合,这里就用到前面提到的数据关联和状态估计方法。通过数据关联确定不同传感器数据的对应关系,再用状态估计预测目标的下一状态。
python
# 假设已经有来自两个传感器的检测数据
sensor1_detections = [(100, 200, 150, 250), (300, 400, 350, 450)]
sensor2_detections = [(105, 205, 155, 255), (305, 405, 355, 455)]
# 数据关联(简单距离匹配示例)
associated_detections = []
for det1 in sensor1_detections:
min_dist = float('inf')
best_match = None
for det2 in sensor2_detections:
dist = euclidean_distance((det1[0], det1[1]), (det2[0], det2[1]))
if dist < min_dist:
min_dist = dist
best_match = det2
associated_detections.append((det1, best_match))
# 状态估计与跟踪
for assoc in associated_detections:
measurement = np.matrix([[assoc[0][0]], [assoc[0][1]]])
predicted_state = kf.predict()
updated_state = kf.update(measurement)
print(f"预测状态: {predicted_state}, 更新后状态: {updated_state}")这段代码展示了简单的数据关联和状态估计过程,实际应用中会更加复杂,可能涉及多传感器融合算法如加权融合、贝叶斯融合等。
从零构建一个多目标多传感器融合跟踪器是个复杂但有趣的过程,从理解算法原理到一步步实现,每个环节都充满挑战与惊喜,希望这篇文章能给你一些启发,让你在这个领域迈出探索的步伐。