【强化学习实验】- 策略梯度算法

涛涛北京2025-12-16 18:57

1.实验内容

策略梯度算法文章中2.2 策略梯度算法。

通俗总结

① 优胜劣汰

② 学如逆水行舟，不进则退。

2.实验目标

2.1 构建策略模型

python 复制代码

class PolicyNet(torch.nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(PolicyNet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
    # 输入就是state, 输出就是一个action分布
    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = self.fc2(x)
        return F.softmax(x, dim=1)

2.2 目标函数及其 loss函数

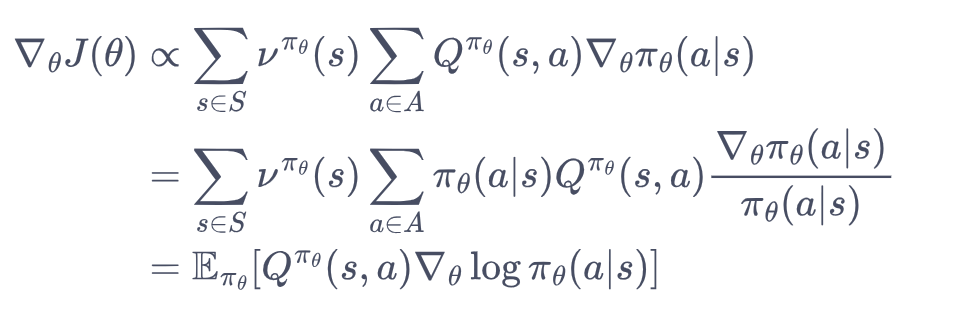
loss = -微分对象=-Q*log概率

python 复制代码

def update(self, transition_dict):
    state_list  = transition_dict['states']
    action_list = transition_dict['actions']
    reward_list = transition_dict['rewards']
    # 每个episode为单位, 计算动作价值的累计收益
    G = 0
    
    # 倒放数据，计算动作的累计收益
    self.optimizer.zero_grad()
    for i in range(len(reward_list)-1, -1, -1):
        state = torch.tensor([state_list[i]]).to(self.device)
        action = torch.tensor([action_list[i]]).view(-1, 1).to(self.device)
        G = reward_list[i] + self.gamma*G
        logP = torch.log(self.policy_net(state).gather(1, action))
        loss = -G*logP
        loss.backward()
    self.optimizer.step()

2.3 思考算法的优缺点

a、仅使用sar数据，可能会限制算法的能力上线

b、无偏，但是方差比较大

3.完整代码

见附件

4.实验结果

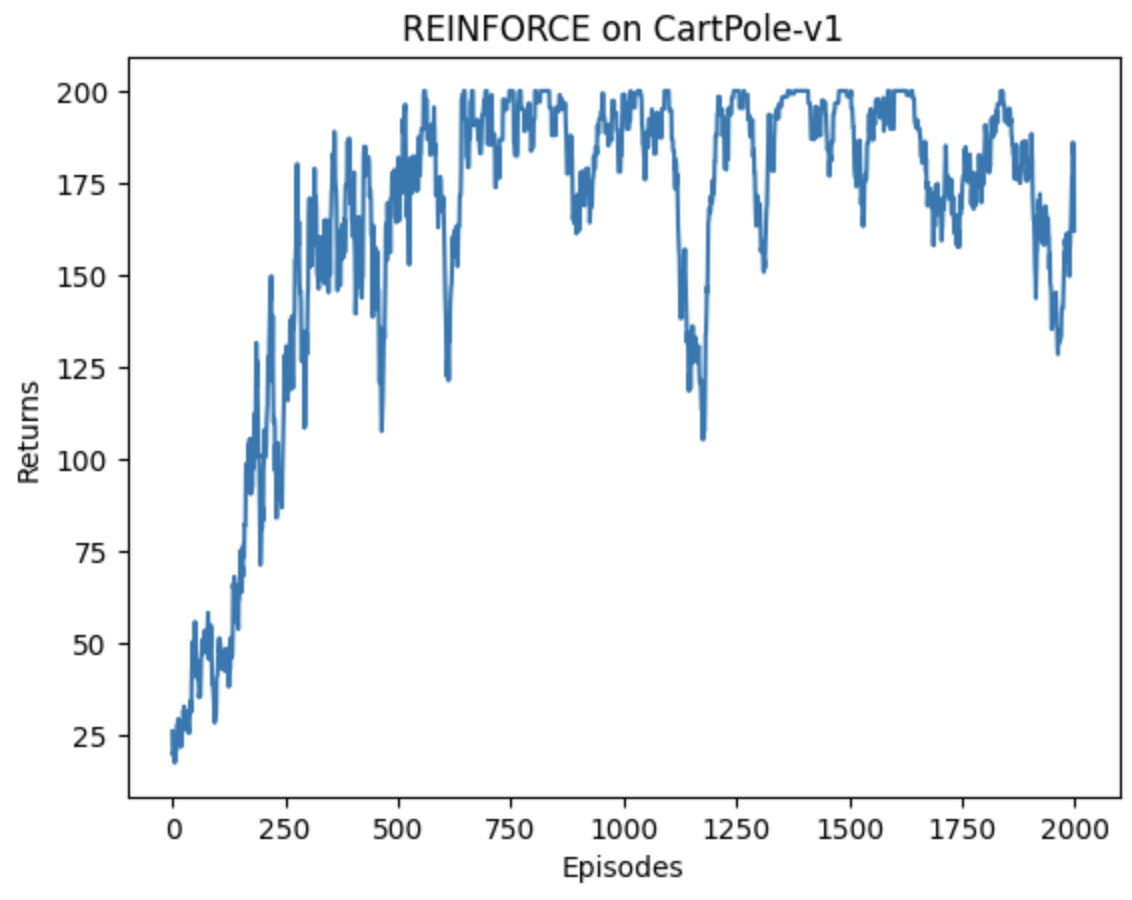
模型训练750个epoch接近收敛，而后震荡收敛。

尝试扩大epoch，效果如下：

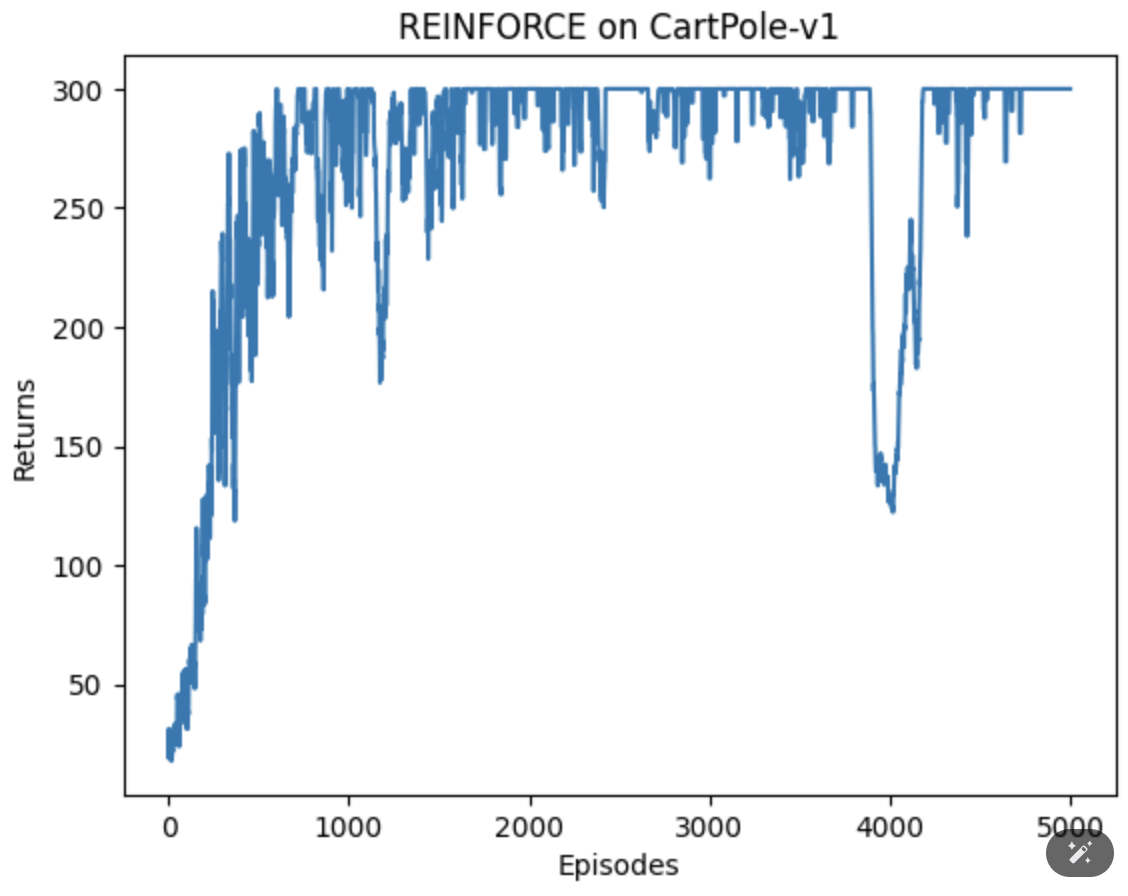
结论：总的来说，可以收敛，但是收敛效果并不是很好，后续和AC算法做一下对比。

有没有小伙伴知道为啥后期收敛效果不好？欢迎评论指教。