
一、AVL树部分
1. 图像部分
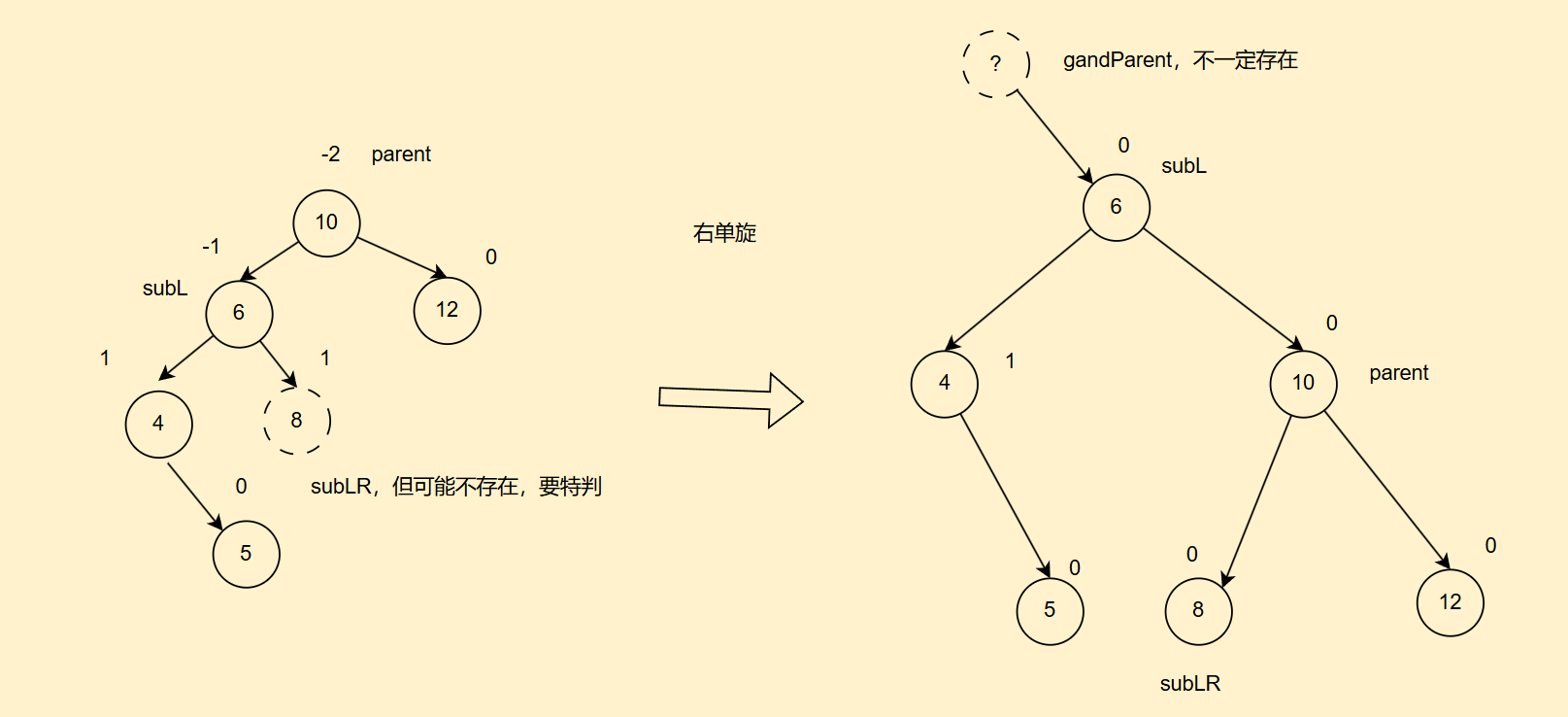
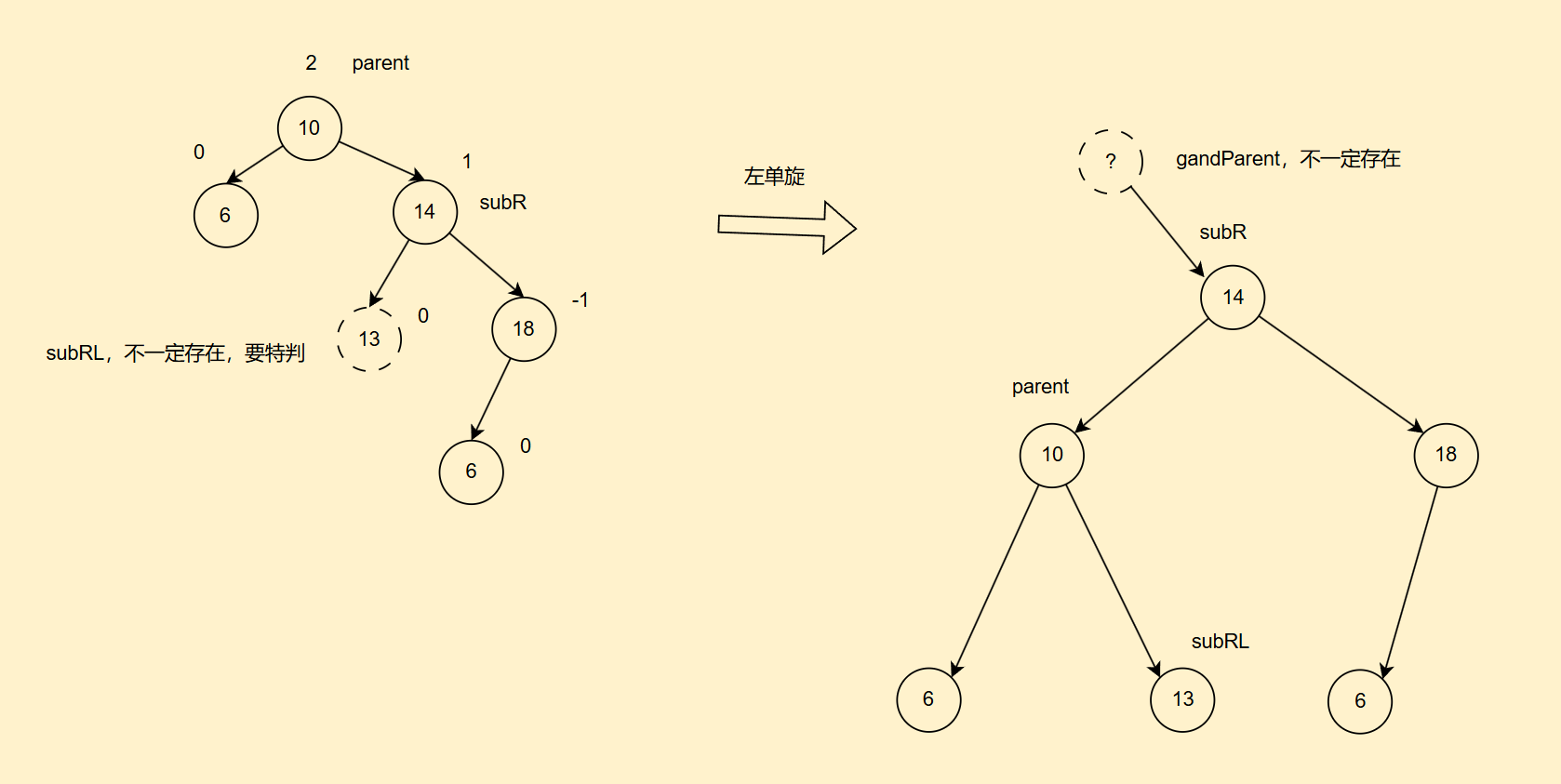
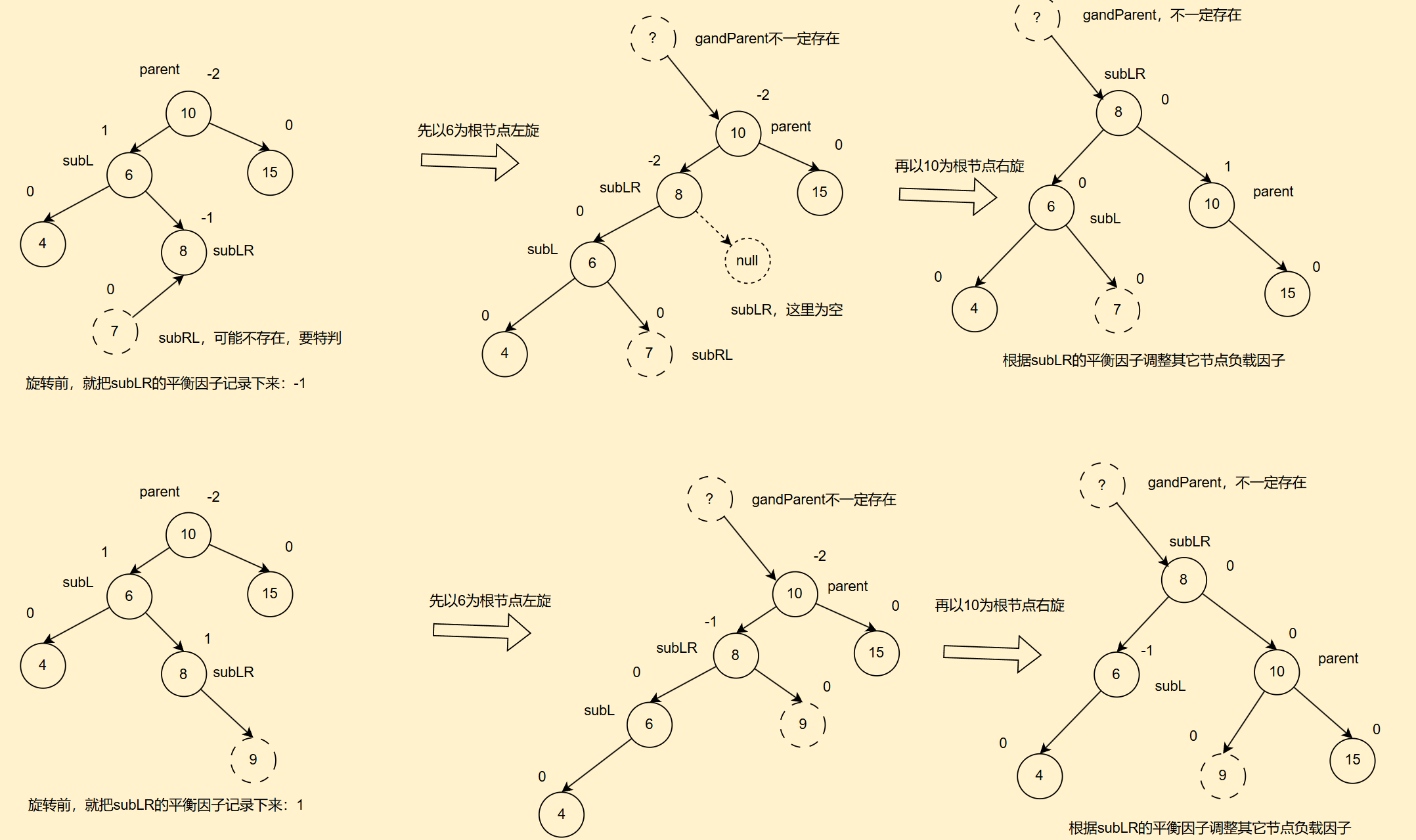
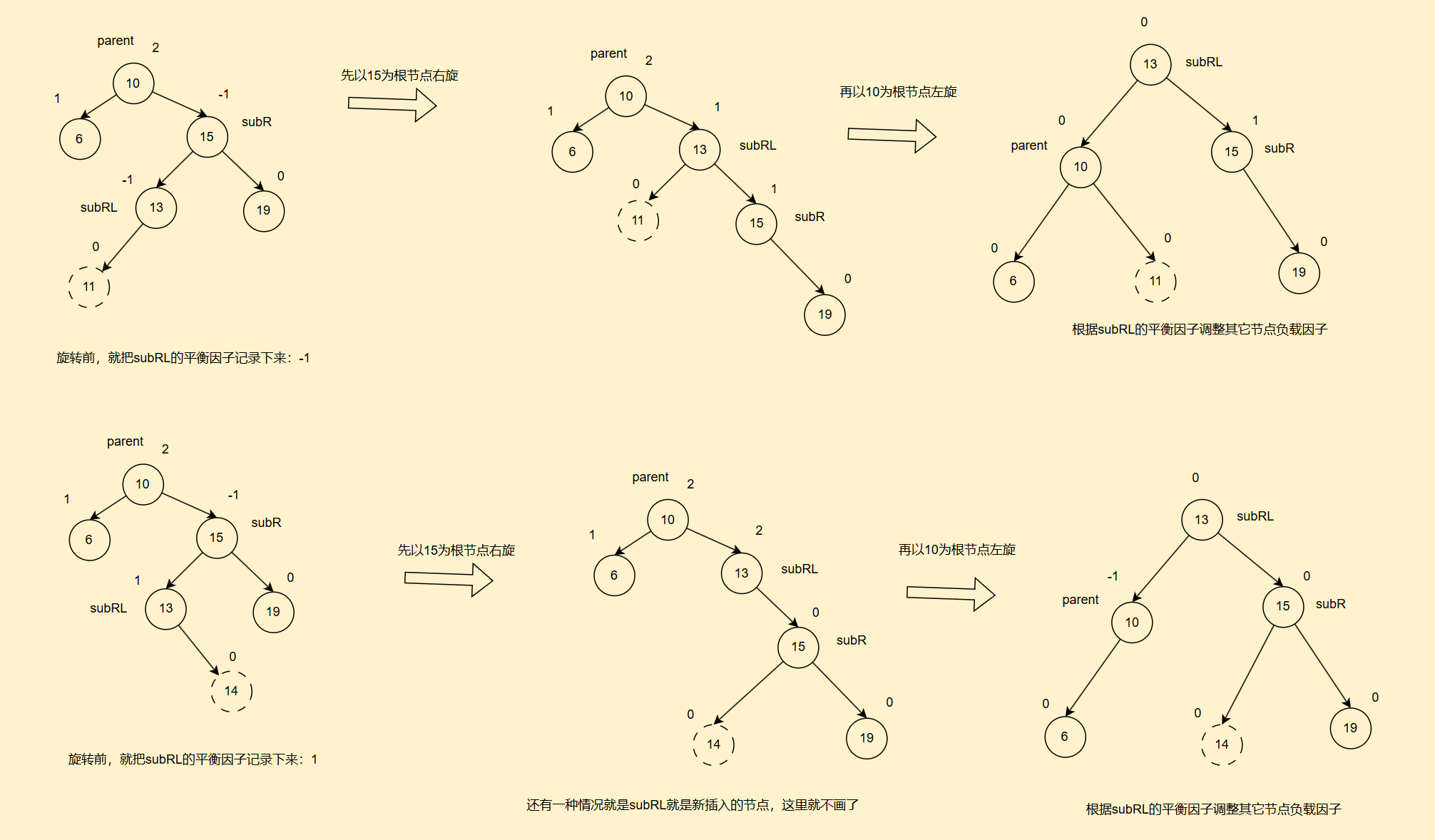
2. 代码部分
java
/**
* @author pluchon
* @create 2026-01-31-10:53
* 作者代码水平一般,难免难看,请见谅
*/
//模拟实现AVL树,本质上还是一个二叉搜索树
public class AVLTree {
//使用孩子双亲表示法
static class AVLTreeNode {
public AVLTreeNode left = null; // 节点的左孩子
public AVLTreeNode right = null; // 节点的右孩子
public AVLTreeNode parent = null; // 节点的双亲
public int val = 0;
//当前节点的平衡因子=右子树高度-左子树的高度
public int bf = 0;
public AVLTreeNode(int val) {
this.val = val;
}
}
//我们规定每个节点的值只能出现一次,后期可以加上计数器
//给一个根节点
private static AVLTreeNode root;
//----插入----
public boolean insert(int value){
//1.先按照正常逻辑插入节点
AVLTreeNode node = new AVLTreeNode(value);
//首先判断根节点是不是空
if(root == null){
root = node;
return true;
}
//如果根节点不是空,则要找到插入位置
AVLTreeNode parent = null;
AVLTreeNode current = root;
while(current != null) {
//开始寻找位置
if (current.val < value) {
//说明插入的值更大,到右边去
parent = current;
current = current.right;
} else if (current.val > value) {
//说明插入的值更小,到左边去
parent = current;
current = current.left;
} else {
//出现重复值
return false;
}
}
//此时current所在的null就是新节点要插入的位置
//此时parent在current(空节点)的父节点
//此时再判断parent值
if(parent.val > value){
parent.left = node;
}else{
parent.right = node;
}
//赋予parent
node.parent = parent;
//2.调整负载因子,此时node的平衡因子默认就是0
//3.同时根据情况判断何种旋转
while(parent != null){
if(parent.right == node){
//说明新插入的节点在parent的右边
parent.bf++;
}else{
parent.bf--;
}
//此时再判断当前一轮更新完毕后的平衡因子
if(parent.bf == 0){
//此时左右子树已经达到平衡了,无需调整,直接跳出循环
break;
}else if(parent.bf == 1 || parent.bf == -1){
//此时只是说明当前的左右子树平衡了,但是不代表连接当前parent的更大子树是平衡的
//因此我们仍需"向上走查看"
node = parent;
//当前parent节点的双亲节点
parent = parent.parent;
}else{
//开启旋转,原则:同号单旋,异号双旋
//说明此时parent.bf == 2 或 parent.bf == -2
//----------------------------------------
//分别是:右子树过高&左子树过高
if(parent.bf == 2){
if(node.bf == 1){
//左单旋
rotateLeft(parent);
}else{
//先右旋,再左旋的双旋
rotateRL(parent);
}
}else{
if(node.bf == 1){
//先左旋,再右旋的双旋
rotateLR(parent);
}else{
//右单旋
rotateRight(parent);
}
}
//旋转完成后整棵树高度已平衡
break;
}
}
//最后返回true
return true;
}
//右单旋
public static void rotateRight(AVLTreeNode parent){
//定义好节点,subL-->node,subLR-->node.right(要转移到节点)
AVLTreeNode subL = parent.left;
AVLTreeNode subLR = subL.right;
//开始迁移
parent.left = subLR;
//此时注意,只有在subLR不为空节点条件下,才可以修改其双亲指向
if(subLR != null){
subLR.parent = parent;
}
//继续修改指向
subL.right = parent;
//注意我们parent有可能是其它节点的子节点,为了避免修改双亲指针丢失原来双亲节点,因此要保存
AVLTreeNode grandParent = parent.parent;
//修改原parent双亲节点
parent.parent = subL;
//此时再判断parent是否是根节点,即是否是一棵独立的子树
if(parent == root){
//根节点变更
root = subL;
//整棵树的起始,自然无双亲节点
subL.parent = null;
}else{
//此时说明parent是其它更高一级的父节点的子节点
//判断位置
if(grandParent.right == parent){
//在右边
grandParent.right = subL;
}else{
//在左边
grandParent.left = subL;
}
//指向正确的双亲节点
subL.parent = grandParent;
}
//调整平衡因子
subL.bf = parent.bf = 0;
}
//左单旋
public static void rotateLeft(AVLTreeNode parent){
AVLTreeNode subR = parent.right;
AVLTreeNode subRL = subR.left;
//开始迁移
parent.right = subRL;
//判断是否为空,改变其双亲节点指向
if(subRL != null){
subRL.parent = parent;
}
//记录原parent的双亲节点
AVLTreeNode grandParent = parent.parent;
//继续调整
subR.left = parent;
//修改原parent双亲节点
parent.parent = subR;
//开始判断
if(parent == root){
//变更整棵树的根节点
root = subR;
root.parent = null;
}else{
//说明原根节点还有它的双亲节点指向它
//看看parent位于什么位置
if(grandParent.right == parent){
grandParent.right = subR;
}else{
grandParent.left = subR;
}
//改变双亲节点指向
subR.parent = grandParent;
}
//调整平衡因子
subR.bf = parent.bf = 0;
}
//先左旋再右旋
public static void rotateLR(AVLTreeNode parent){
//记录节点
AVLTreeNode subL = parent.left;
AVLTreeNode subLR = subL.right;
//提前记录平衡因子,后续有大用
int bf = subLR.bf;
//旋转
rotateLeft(parent.left);
rotateRight(parent);
//调整平衡因子
if(bf == 1) {
//插入在 subLR 的右子树
parent.bf = subLR.bf = 0;
subL.bf = -1;
}else if (bf == -1) {
//插入在 subLR 的左子树
parent.bf = 1;
subLR.bf = subL.bf = 0;
}else if (bf == 0) {
//特殊情况
//subLR自身就是新节点
parent.bf = subLR.bf = subL.bf = 0;
}
//完毕
}
//先右旋再左旋
public static void rotateRL(AVLTreeNode parent){
//记录节点
AVLTreeNode subR = parent.right;
AVLTreeNode subRL = subR.left;
//提前记录平衡因子,后续有大用
int bf = subRL.bf;
//旋转
rotateRight(parent.right);
rotateLeft(parent);
//调整平衡因子
if(bf == 1) {
parent.bf = -1;
subRL.bf = subR.bf = 0;
} else if (bf == -1) {
parent.bf = subRL.bf = 0;
subR.bf = 1;
} else {
parent.bf = subRL.bf = subR.bf = 0;
}
//完毕
}
//----删除----
public boolean remove(int val){ // 去掉 static 方便管理 root
//寻找要删除的节点
AVLTreeNode parent = null;
AVLTreeNode current = root;
while(current != null){
if(current.val < val){
parent = current;
current = current.right;
}else if(current.val > val){
parent = current;
current = current.left;
}else{
//此时找到了我们要删除的节点,执行删除逻辑
removeNode(parent,current);
//删除成功
return true;
}
}
//删除失败
return false;
}
//删除节点核心逻辑
public void removeNode(AVLTreeNode parent,AVLTreeNode current){
// 用于记录真正开始调整平衡因子的起点节点及其父节点
AVLTreeNode updatePos = current; // 记录当前节点,用于判定删除方向
AVLTreeNode updateParent = parent;
//这个写过,要分三种情况
if(current.left == null){//左节点位空
//再分三种情况,根节点root/在parent左子树上/在parent右子树上
if(current == root){
root = current.right;
if(root != null) root.parent = null;
}else if(current == parent.left){
parent.left = current.right;
if(current.right != null) current.right.parent = parent;
}else if(current == parent.right){
parent.right = current.right;
if(current.right != null) current.right.parent = parent;
}
}else if(current.right == null){//右节点为空
if(current == root){
root = current.left;
if(root != null) root.parent = null;
}else if(current == parent.left){
parent.left = current.left;
if(current.left != null) current.left.parent = parent;
}else if(current == parent.right){
parent.right = current.left;
if(current.left != null) current.left.parent = parent;
}
}else{//都不为空情况
//需要去寻找左子树的最大值,值赋予被删除的这个节点
AVLTreeNode leftMax = current.left;
AVLTreeNode leftMaxParent = current;
//搜索:左子树的最大值应该一直往右找
while(leftMax.right != null){
leftMaxParent = leftMax;
leftMax = leftMax.right;
}
//此时搜索到了,赋值
current.val = leftMax.val;
// 物理删除 leftMax 节点,并重新确定调整起点
updatePos = leftMax;
updateParent = leftMaxParent;
if(leftMaxParent.left == leftMax){
leftMaxParent.left = leftMax.left;
}else{
leftMaxParent.right = leftMax.left;
}
if(leftMax.left != null) leftMax.left.parent = leftMaxParent;
}
//正式调整平衡因子
fixAfterDeletion(updateParent, updatePos);
}
public void fixAfterDeletion(AVLTreeNode parent, AVLTreeNode node){
while(parent != null){
//不能直接用 == 判断,因为指针可能已经改了
//如果 parent 的左孩子是 node,或者原本 node 的值小于 parent 的值
//node != null && node.val < parent.val是为了保证在值替换删除的时候也很准
/*
左子树的所有节点值一定小于父节点,右子树的所有节点值一定大于父节点
如果 node.val < parent.val,那么无论 node 现在在哪里,它曾经一定属于 parent 的左子树
既然删掉的是左边的东西,右边就相对变重了,所以 parent.bf++ 是绝对正确的
*/
if(parent.left == node || (node != null && node.val < parent.val)){
parent.bf++;
}else{
parent.bf--;
}
//判断bf值,决定后续动作
if(parent.bf == 1 || parent.bf == -1){
break;
}else if(parent.bf == 0){
node = parent;
parent = parent.parent;
}else{
AVLTreeNode pParent = parent.parent;
if (parent.bf == 2) {//右边过重
AVLTreeNode subR = parent.right;
//空指针预防:只有在 subR 存在时才读取 bf
if (subR != null && subR.bf == 1) {
rotateLeft(parent);
node = subR;
parent = pParent;
} else if (subR != null && subR.bf == -1) {
rotateRL(parent);
node = parent.parent;
parent = pParent;
} else if (subR != null) {
rotateLeft(parent);
parent.bf = 1;
subR.bf = -1;
break;
}
} else {//parent.bf == -2
AVLTreeNode subL = parent.left;
if (subL != null && subL.bf == -1) {
rotateRight(parent);
node = subL;
parent = pParent;
} else if (subL != null && subL.bf == 1) {
rotateLR(parent);
node = parent.parent;
parent = pParent;
} else if (subL != null) {
rotateRight(parent);
parent.bf = -1;
subL.bf = 1;
break;
}
}
}
}
}
//------以下是辅助测试方法------
// 中序遍历:验证是否还是二叉搜索树(应该是升序)
public void inOrder(AVLTreeNode root) {
if (root == null) return;
inOrder(root.left);
System.out.print(root.val + " ");
inOrder(root.right);
}
// 获取高度:辅助验证平衡性
private int height(AVLTreeNode root) {
if (root == null) return 0;
return Math.max(height(root.left), height(root.right)) + 1;
}
// 综合验证:检查每个节点的平衡因子是否正确,且高度差是否异常
public boolean isBalanced(AVLTreeNode root) {
if (root == null) return true;
int leftH = height(root.left);
int rightH = height(root.right);
// 验证平衡因子是否匹配实际高度差
if (rightH - leftH != root.bf) {
System.out.println("节点 " + root.val + " 平衡因子异常!实际 bf: " + (rightH - leftH) + ", 记录 bf: " + root.bf);
return false;
}
// 验证高度差绝对值是否超过 1
if (Math.abs(rightH - leftH) >= 2) {
System.out.println("节点 " + root.val + " 失衡!高度差: " + Math.abs(rightH - leftH));
return false;
}
return isBalanced(root.left) && isBalanced(root.right);
}
//------测试------
public static void main(String[] args) {
AVLTree tree = new AVLTree();
// --- 测试 1: RR 型 (触发左单旋) ---
System.out.println("--- 测试 1: RR 型 (左单旋) ---");
int[] rrArray = {10, 20, 30};
for (int x : rrArray) tree.insert(x);
System.out.print("中序遍历: "); tree.inOrder(root);
System.out.println("\n是否平衡: " + tree.isBalanced(root));
// 清空根节点进行下一轮测试 (如果是 static root)
root = null;
// --- 测试 2: LL 型 (触发右单旋) ---
System.out.println("\n--- 测试 2: LL 型 (右单旋) ---");
int[] llArray = {30, 20, 10};
for (int x : llArray) tree.insert(x);
System.out.print("中序遍历: "); tree.inOrder(root);
System.out.println("\n是否平衡: " + tree.isBalanced(root));
root = null;
// --- 测试 3: LR 型 (触发左右双旋) ---
System.out.println("\n--- 测试 3: LR 型 (左右双旋) ---");
int[] lrArray = {30, 10, 20};
for (int x : lrArray) tree.insert(x);
System.out.print("中序遍历: "); tree.inOrder(root);
System.out.println("\n是否平衡: " + tree.isBalanced(root));
root = null;
// --- 测试 4: RL 型 (触发右左双旋) ---
System.out.println("\n--- 测试 4: RL 型 (右左双旋) ---");
int[] rlArray = {10, 30, 20};
for (int x : rlArray) tree.insert(x);
System.out.print("中序遍历: "); tree.inOrder(root);
System.out.println("\n是否平衡: " + tree.isBalanced(root));
root = null;
// --- 测试 5: 综合随机大量数据 ---
System.out.println("\n--- 测试 5: 综合压力测试 ---");
int[] data = {16, 3, 7, 11, 9, 26, 18, 14, 15};
for (int x : data) tree.insert(x);
System.out.print("中序遍历: "); tree.inOrder(root);
System.out.println("\n最终是否平衡: " + tree.isBalanced(root));
//----压测----
// --- 测试 6: 连续递增 (RR 压力测试) ---
System.out.println("\n--- 测试 6: 连续递增 (多次 RR) ---");
int[] data6 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
root = null; // 重置
for (int x : data6) tree.insert(x);
System.out.println("中序遍历: "); tree.inOrder(root);
System.out.println("\n是否平衡: " + tree.isBalanced(root));
// --- 测试 7: 连续递减 (LL 压力测试) ---
System.out.println("\n--- 测试 7: 连续递减 (多次 LL) ---");
int[] data7 = {10, 9, 8, 7, 6, 5, 4, 3, 2, 1};
root = null;
for (int x : data7) tree.insert(x);
System.out.println("中序遍历: "); tree.inOrder(root);
System.out.println("\n是否平衡: " + tree.isBalanced(root));
// --- 测试 8: 嵌套 LR/RL ---
System.out.println("\n--- 测试 8: 嵌套双旋测试 ---");
int[] data8 = {50, 25, 75, 15, 35, 65, 85, 30, 40};
root = null;
for (int x : data8) tree.insert(x);
System.out.println("中序遍历: "); tree.inOrder(root);
System.out.println("\n是否平衡: " + tree.isBalanced(root));
// --- 测试 9: 锯齿插入 ---
System.out.println("\n--- 测试 9: 锯齿形 (RL 深度触发) ---");
int[] data9 = {100, 50, 150, 120, 130, 110, 125};
root = null;
for (int x : data9) tree.insert(x);
System.out.println("中序遍历: "); tree.inOrder(root);
System.out.println("\n是否平衡: " + tree.isBalanced(root));
// --- 测试 10: 密集型测试 ---
System.out.println("\n--- 测试 10: 大规模密集数据 ---");
int[] data10 = {20, 10, 30, 5, 15, 25, 35, 2, 8, 12, 18, 22, 28, 32, 38};
root = null;
for (int x : data10) tree.insert(x);
System.out.println("中序遍历: "); tree.inOrder(root);
System.out.println("\n最终验证: " + tree.isBalanced(root));
// --- 测试 11: 基础删除测试 (叶子/单孩子/双孩子) ---
System.out.println("\n--- 测试 11: 基础删除测试 ---");
root = null;
int[] data11 = {50, 30, 70, 20, 40, 60, 80};
for (int x : data11) tree.insert(x);
System.out.println("删除叶子 20:"); tree.remove(20);
System.out.println("是否平衡: " + tree.isBalanced(root));
System.out.println("删除单孩子 70 (80 顶替):"); tree.remove(70);
System.out.println("是否平衡: " + tree.isBalanced(root));
System.out.println("删除根节点 50 (左子树最大值顶替):"); tree.remove(50);
System.out.print("中序遍历: "); tree.inOrder(root);
System.out.println("\n是否平衡: " + tree.isBalanced(root));
// --- 测试 12: 删除触发单旋 ---
System.out.println("\n--- 测试 12: 删除触发单旋 (LL/RR) ---");
root = null;
int[] data12 = {40, 20, 50, 10, 30}; // 构造一个稍微偏左的树
for (int x : data12) tree.insert(x);
System.out.println("删除 50 触发右单旋:");
tree.remove(50);
System.out.print("中序遍历: "); tree.inOrder(root);
System.out.println("\n是否平衡: " + tree.isBalanced(root));
// --- 测试 13: 删除触发双旋 ---
System.out.println("\n--- 测试 13: 删除触发双旋 (LR/RL) ---");
root = null;
int[] data13 = {40, 20, 50, 25};
for (int x : data13) tree.insert(x);
System.out.println("删除 50 触发 LR 双旋:");
tree.remove(50);
System.out.print("中序遍历: "); tree.inOrder(root);
System.out.println("\n是否平衡: " + tree.isBalanced(root));
// --- 测试 14: 连环旋转压测 (最核心测试) ---
// 构造一棵特殊树,使得删除一个节点后,失衡信号一路上传触发多次旋转
System.out.println("\n--- 测试 14: 连环旋转压测 (Cascading Rotations) ---");
root = null;
int[] data14 = {50, 25, 80, 15, 35, 60, 90, 10, 20, 30, 40, 70, 100, 5, 65};
for (int x : data14) tree.insert(x);
System.out.println("删除 100 可能会引发连锁反应:");
tree.remove(100);
System.out.print("中序遍历: "); tree.inOrder(root);
System.out.println("\n最终验证: " + tree.isBalanced(root));
// --- 测试 15: 全量随机删除测试 ---
System.out.println("\n--- 测试 15: 顺序删除清理全树 ---");
int[] data15 = {16, 3, 7, 11, 9, 26, 18, 14, 15};
root = null;
for (int x : data15) tree.insert(x);
System.out.println("开始清空树...");
for (int x : data15) {
tree.remove(x);
if (root != null && !tree.isBalanced(root)) {
System.out.println("错误:删除 " + x + " 后失衡!");
}
}
System.out.println("清空完成,当前根节点: " + root);
}
}二、红黑树部分
1. 删除节点的四种情况示意图
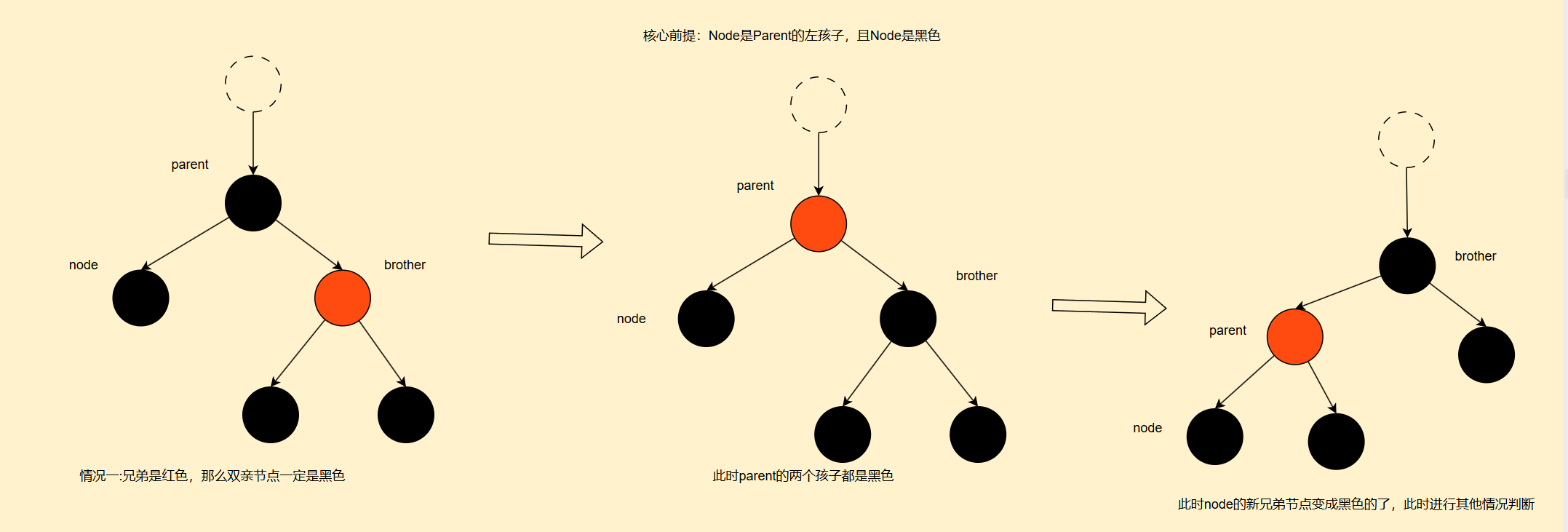
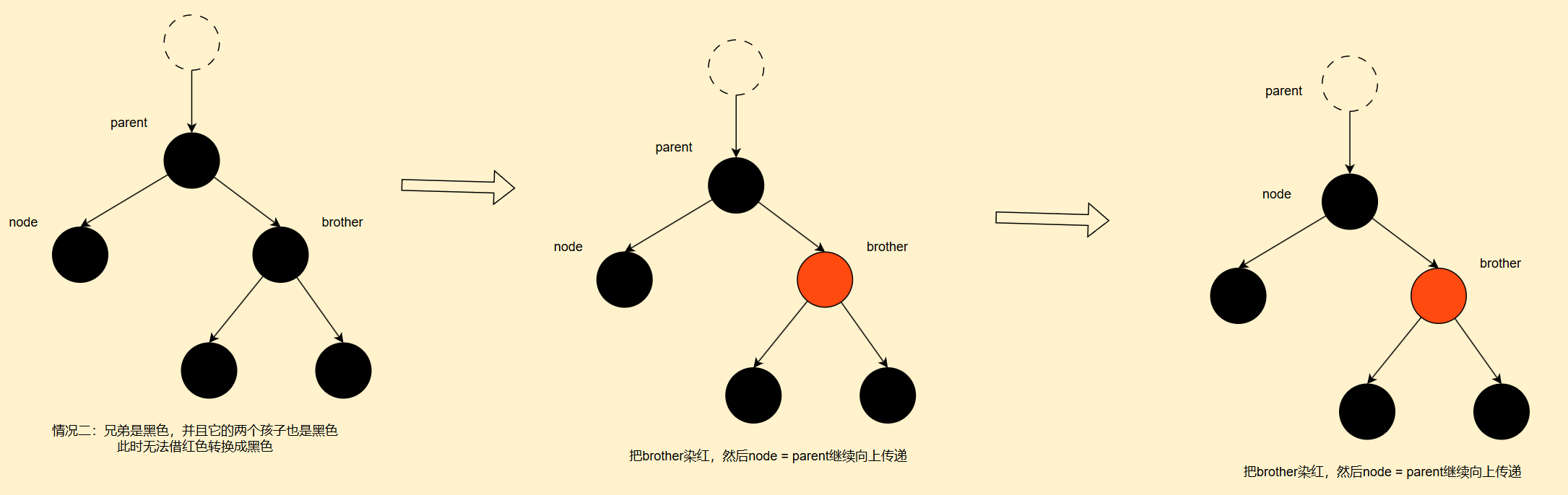
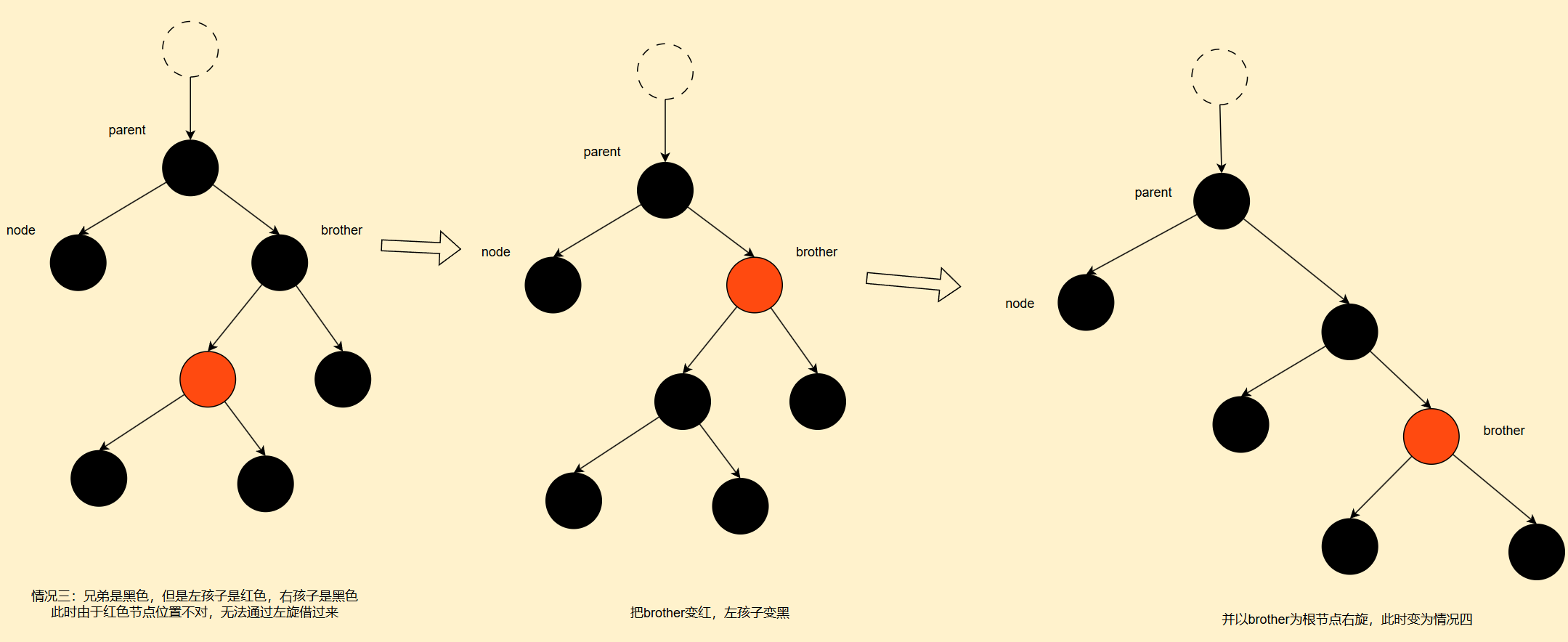
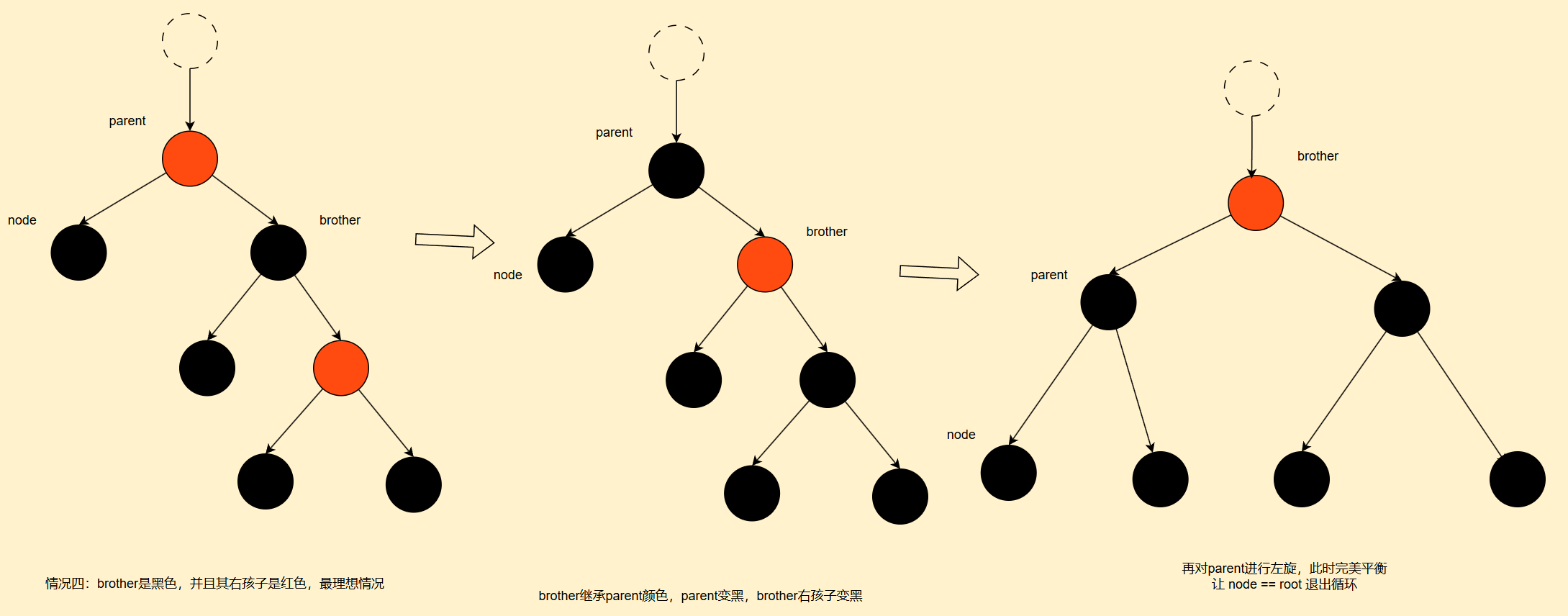
2. 代码部分
java
public enum Color {
BLACK,RED;
}
java
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Random;
/**
* @author pluchon
* @create 2026-02-04-14:06
* 作者代码水平一般,难免难看,请见谅
*/
public class RBTree {
static class RBTreeNode {
public RBTreeNode left;
public RBTreeNode right;
public RBTreeNode parent;
public int val;
public Color color = Color.RED;
public RBTreeNode(int val) {
this.val = val;
}
}
public static RBTreeNode root;
//插入
public boolean insert(int value){
//1. 首先按照正常的二叉搜索树插入节点
RBTreeNode node = new RBTreeNode(value);
//首先判断根节点是不是空
if(root == null){
root = node;
root.color = Color.BLACK;
return true;
}
//如果根节点不是空,则要找到插入位置
RBTreeNode parent = null;
RBTreeNode current = root;
while(current != null) {
if (current.val < value) {
parent = current;
current = current.right;
} else if (current.val > value) {
parent = current;
current = current.left;
} else {
return false;
}
}
if(parent.val > value){
parent.left = node;
}else{
parent.right = node;
}
node.parent = parent;
//重新让current指向新插入的节点,用于后续平衡调整
current = node;
//2. 此时进行调整
while(parent != null && parent.color == Color.RED){
RBTreeNode grandParent = parent.parent;
if(grandParent == null) break; // 安全检查
if(grandParent.left == parent){
RBTreeNode parentBrother = grandParent.right;
if(parentBrother != null && parentBrother.color == Color.RED){
parent.color = Color.BLACK;
parentBrother.color = Color.BLACK;
grandParent.color = Color.RED;
current = grandParent;
parent = current.parent;
}else{
if(parent.right == current){
rotateLeft(parent);
//交换指针,确保下一步单旋时逻辑正确
RBTreeNode temp = parent;
parent = current;
current = temp;
}
rotateRight(grandParent);
parent.color = Color.BLACK;
grandParent.color = Color.RED;
}
}else{
RBTreeNode parentBrother = grandParent.left;
if(parentBrother != null && parentBrother.color == Color.RED){
parent.color = Color.BLACK;
parentBrother.color = Color.BLACK;
grandParent.color = Color.RED;
current = grandParent;
parent = current.parent;
}else{
if(parent.left == current){
rotateRight(parent);
RBTreeNode temp = parent;
parent = current;
current = temp;
}
rotateLeft(grandParent);
parent.color = Color.BLACK;
grandParent.color = Color.RED;
}
}
}
root.color = Color.BLACK;
return true;
}
//删除
public boolean remove(int val){ // 去掉 static 方便管理 root
//寻找要删除的节点
RBTreeNode parent = null;
RBTreeNode current = root;
while(current != null){
if(current.val < val){
parent = current;
current = current.right;
}else if(current.val > val){
parent = current;
current = current.left;
}else{
//此时找到了我们要删除的节点,执行删除逻辑
removeNode(parent,current);
//删除成功
return true;
}
}
//删除失败
return false;
}
//二叉搜索树的删除逻辑
public static void removeNode(RBTreeNode parent, RBTreeNode current) {
//记录真正被物理删除的节点的颜色
Color removedColor;
//updatePos应该是"接替者",updateParent 是接替者的父节点
RBTreeNode updatePos;
RBTreeNode updateParent;
if (current.left == null) {
//情况A: 左为空,右孩子顶上去
removedColor = current.color;
updatePos = current.right;
//顶替者是右孩子
updateParent = parent;
if (current == root) {
root = updatePos;
if (root != null) root.parent = null;
} else if (current == parent.left) {
parent.left = updatePos;
if (updatePos != null) updatePos.parent = parent;
} else {
parent.right = updatePos;
if (updatePos != null) updatePos.parent = parent;
}
} else if (current.right == null) {
//情况B: 右为空,左孩子顶上去
removedColor = current.color;
updatePos = current.left;
//顶替者是左孩子
updateParent = parent;
if (current == root) {
root = updatePos;
if (root != null) root.parent = null;
} else if (current == parent.left) {
parent.left = updatePos;
if (updatePos != null) updatePos.parent = parent;
} else {
parent.right = updatePos;
if (updatePos != null) updatePos.parent = parent;
}
} else {
//情况C: 都不为空,找左子树最大值 (前驱)
RBTreeNode leftMax = current.left;
RBTreeNode leftMaxParent = current;
while (leftMax.right != null) {
leftMaxParent = leftMax;
leftMax = leftMax.right;
}
//把leftMax的值给current,改为删除leftMax节点
current.val = leftMax.val;
//真正消失在树里的颜色是leftMax的
removedColor = leftMax.color;
//leftMax是最大值,只可能有左孩子
updatePos = leftMax.left;
updateParent = leftMaxParent;
//物理删除leftMax
if (leftMaxParent.left == leftMax) {
leftMaxParent.left = updatePos;
} else {
leftMaxParent.right = updatePos;
}
if (updatePos != null) updatePos.parent = leftMaxParent;
}
//只有删除黑色节点,才需要通过AdjustColor补齐那一层黑色
if (removedColor == Color.BLACK) {
AdjustColor(updatePos, updateParent);
}
}
//调整颜色
public static void AdjustColor(RBTreeNode node, RBTreeNode parent) {
//如果node是红色,直接染黑就补全了缺失的黑色,循环结束
// 如果node到达根节点,黑色少一层也无妨,循环结束
while (node != root && (node == null || node.color == Color.BLACK)) {
if (node == parent.left) {
RBTreeNode brother = parent.right;
//1.兄弟是红色
if (brother != null && brother.color == Color.RED) {
brother.color = Color.BLACK;
parent.color = Color.RED;
rotateLeft(parent);
brother = parent.right; // 刷新兄弟节点
}
//2. 兄弟的两个孩子都是黑色 (包含 null)
if ((brother.left == null || brother.left.color == Color.BLACK) &&
(brother.right == null || brother.right.color == Color.BLACK)) {
brother.color = Color.RED;
node = parent; // 向上冒泡
parent = (node != null) ? node.parent : null;
} else {
//3.兄弟右孩子是黑色,左孩子是红色
if (brother.right == null || brother.right.color == Color.BLACK) {
if (brother.left != null) brother.left.color = Color.BLACK;
brother.color = Color.RED;
rotateRight(brother);
brother = parent.right; // 刷新兄弟
}
//4.兄弟右孩子是红色
brother.color = parent.color;
parent.color = Color.BLACK;
if (brother.right != null) brother.right.color = Color.BLACK;
rotateLeft(parent);
node = root; // 强制结束
}
} else {
// 镜像对称:node 是右孩子
RBTreeNode brother = parent.left;
if (brother != null && brother.color == Color.RED) {
brother.color = Color.BLACK;
parent.color = Color.RED;
rotateRight(parent);
brother = parent.left;
}
if ((brother.right == null || brother.right.color == Color.BLACK) &&
(brother.left == null || brother.left.color == Color.BLACK)) {
brother.color = Color.RED;
node = parent;
parent = (node != null) ? node.parent : null;
} else {
if (brother.left == null || brother.left.color == Color.BLACK) {
if (brother.right != null) brother.right.color = Color.BLACK;
brother.color = Color.RED;
rotateLeft(brother);
brother = parent.left;
}
brother.color = parent.color;
parent.color = Color.BLACK;
if (brother.left != null) brother.left.color = Color.BLACK;
rotateRight(parent);
node = root;
}
}
}
//不管是因为问题上移遇到了红节点,还是接替者本身就是红节点,只要我能把你染黑,我就能平掉那笔'黑债'
//如果实在没红节点可染,最后把根节点染黑也是符合性质要求的
if (node != null) node.color = Color.BLACK;
}
//验证部分
public boolean isValidRBTree(){
if(root == null) return true;
if(root.color != Color.BLACK) return false;
int expectedBlackCount = 0;
RBTreeNode current = root;
while(current != null){
if(current.color == Color.BLACK) expectedBlackCount++;
current = current.left;
}
// 具体校验逻辑
return checkStructure(root, 0, expectedBlackCount);
}
//参数逻辑:pathBlackNodeCount是累加值,expectedBlackCount是目标值
public static boolean checkStructure(RBTreeNode root, int pathBlackNodeCount, int expectedBlackCount){
if(root == null){
return pathBlackNodeCount == expectedBlackCount;
}
RBTreeNode parent = root.parent;
if(parent != null && parent.color == Color.RED && root.color == Color.RED){
return false;
}
if(root.color == Color.BLACK){
pathBlackNodeCount++; //这里累加当前路径的黑节点
}
//同事城楼才返回
return checkStructure(root.left, pathBlackNodeCount, expectedBlackCount)
&& checkStructure(root.right, pathBlackNodeCount, expectedBlackCount);
}
//右单旋
public static void rotateRight(RBTreeNode parent){
RBTreeNode subL = parent.left;
RBTreeNode subLR = subL.right;
parent.left = subLR;
if(subLR != null){
subLR.parent = parent;
}
subL.right = parent;
RBTreeNode grandParent = parent.parent;
parent.parent = subL;
if(parent == root){
root = subL;
subL.parent = null;
}else{
if(grandParent.right == parent) grandParent.right = subL;
else grandParent.left = subL;
subL.parent = grandParent;
}
}
//左单旋
public static void rotateLeft(RBTreeNode parent){
RBTreeNode subR = parent.right;
RBTreeNode subRL = subR.left;
parent.right = subRL;
if(subRL != null){
subRL.parent = parent;
}
RBTreeNode grandParent = parent.parent;
subR.left = parent;
parent.parent = subR;
if(parent == root){
root = subR;
root.parent = null;
}else{
if(grandParent.right == parent) grandParent.right = subR;
else grandParent.left = subR;
subR.parent = grandParent;
}
}
//中序遍历
public static void inorder(RBTreeNode root){
if(root == null) return;
inorder(root.left);
System.out.print(root.val + " ");
inorder(root.right);
}
// 辅助方法:计算高度
public static int getTreeHeight(RBTreeNode node) {
if (node == null) return 0;
return Math.max(getTreeHeight(node.left), getTreeHeight(node.right)) + 1;
}
public static void main(String[] args) {
RBTree tree = new RBTree();
System.out.println("--- 基础测试:1-10 顺序插入 ---");
for (int i = 1; i <= 10; i++) tree.insert(i);
System.out.println("合法性验证: " + tree.isValidRBTree());
System.out.print("中序遍历结果: ");
inorder(RBTree.root);
System.out.println();
System.out.println("\n--- 极端测试:大数据量压测 (10万) ---");
RBTree bigTree = new RBTree();
List<Integer> list = new ArrayList<>();
for (int i = 0; i < 100000; i++) list.add(i);
Collections.shuffle(list);
long start = System.currentTimeMillis();
for (int v : list) bigTree.insert(v);
long end = System.currentTimeMillis();
System.out.println("耗时: " + (end - start) + "ms");
System.out.println("合法性验证: " + bigTree.isValidRBTree());
// --- 补充测试 1:顺序删除测试 ---
System.out.println("--- 补充测试 1:顺序删除测试 ---");
for (int i = 1; i <= 100; i++) tree.insert(i);
boolean isOk = true;
for (int i = 1; i <= 100; i++) {
tree.remove(i);
if (!tree.isValidRBTree()) {
System.out.println("删除 " + i + " 后,红黑树失效!");
isOk = false;
break;
}
}
System.out.println("顺序删除验证结果: " + (isOk ? "PASS" : "FAIL"));
System.out.println("\n--- 补充测试 2:混合随机压测 ---");
RBTree mixTree = new RBTree();
Random random = new Random();
List<Integer> activeNodes = new ArrayList<>();
//随机插入 10000 个
for (int i = 0; i < 10000; i++) {
int val = random.nextInt(100000);
if (mixTree.insert(val)) {
activeNodes.add(val);
}
}
System.out.println("成功插入节点数: " + activeNodes.size());
Collections.shuffle(activeNodes);
//删除数量不能超过 activeNodes 的实际大小
int deleteTarget = Math.min(activeNodes.size(), 5000);
int deleteCount = 0;
for (int i = 0; i < deleteTarget; i++) {
int toRemove = activeNodes.get(i);
if (mixTree.remove(toRemove)) {
deleteCount++;
if (!mixTree.isValidRBTree()) {
System.out.println("随机删除出错!值: " + toRemove);
isOk = false;
break;
}
}
}
System.out.println("成功随机删除节点数: " + deleteCount + ",合法性验证: " + mixTree.isValidRBTree());
System.out.println("\n--- 补充测试 3:性能高度测试 ---");
// 插入 10 万个随机数,查看高度
RBTree perfTree = new RBTree();
for (int i = 0; i < 100000; i++) {
perfTree.insert(random.nextInt(1000000));
}
int height = getTreeHeight(perfTree.root);
System.out.println("10万节点红黑树高度: " + height);
System.out.println("理论最大高度约为: " + (2 * (Math.log(100000) / Math.log(2))));
}
}感谢你的阅读