岛屿数量
题目描述
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
'1','1','1','1','0'\], \['1','1','0','1','0'\], \['1','1','0','0','0'\], \['0','0','0','0','0'
]
输出:1
示例 2:
输入:grid = [
'1','1','0','0','0'\], \['1','1','0','0','0'\], \['0','0','1','0','0'\], \['0','0','0','1','1'
]
输出:3
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 '0' 或 '1'
求解
不管岛屿是啥形状,都满足:
- 单元格值为 1(陆地);
- 上下左右四个方向相连(斜向不算,比如 (0,0) 和 (1,1) 不算连通);
就属于同一个岛屿。
可以把 DFS 理解为"找人":
- 你站在一块陆地上(起点),喊一声 "我的同伙都出来!";
count++ - 你的上下左右邻居(陆地)听到后,各自再喊一声(递归),让他们的邻居也出来;上下左右都dfs;
- 直到所有连通的陆地都被喊到(标记为 0),这一群人就是 "一个岛屿";
- 你继续逛网格,遇到新的、没被喊过的陆地,重复上述过程,每遇到一次就多一个岛屿。
DFS求解代码如下:
js
var numIslands = function(grid) {
if (!grid || grid.length === 0 || grid[0].length === 0) {
return 0;
}
// 求连通分量 的数量
let ans = 0;
let m = grid.length;
let n = grid[0].length;
const dfs = (x, y) => {
if (x < 0 || x >= m || y < 0 || y >= n || grid[x][y] !== '1') {
return
}
grid[x][y] = '0';
dfs(x - 1, y);
dfs(x + 1, y);
dfs(x, y - 1);
dfs(x, y + 1);
}
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (grid[i][j] === '1') {
ans++;
dfs(i, j);
}
}
}
return ans;
};也可以使用广度优先搜索进行解答:
BFS(广度优先搜索)的核心是「层层扩散」:找到一块未访问的陆地后,用队列存储当前陆地的所有邻接陆地,逐个处理并标记为已访问,直到队列空(当前岛屿的所有连通陆地都处理完)。
和 DFS 相比,DFS 是「一条路走到黑」(递归 / 栈),BFS 是「先扫平当前层,再扫下一层」(队列),最终统计「触发 BFS 的次数」就是岛屿数量。
js
var numIslands = function(grid) {
if (!grid || grid.length === 0 || grid[0].length === 0) {
return 0;
}
let m = grid.length;
let n = grid[0].length;
let ans = 0;
let dirs = [[-1, 0], [1, 0], [0, -1], [0, 1]];
const bfs = (x, y) => {
const queue = [[x, y]];
grid[x][y] = '0';
while(queue.length > 0) {
let [currX, currY] = queue.shift();
for (let [a, b] of dirs) {
let dx = currX + a;
let dy = currY + b;
if (dx >= 0 && dx < m && dy >= 0 && dy < n && grid[dx][dy] === '1') {
grid[dx][dy] = '0';
queue.push([dx, dy]);
}
}
}
}
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (grid[i][j] === '1') {
ans++;
bfs(i, j);
}
}
}
return ans;
};方法3:并查集
并查集(Union-Find)的核心是管理连通性:
- 将每个「陆地单元格 (i,j)」映射为唯一的一维编号(如
i * n + j),海洋单元格无需处理; - 遍历所有陆地单元格,将其与上下左右的陆地单元格合并(归为同一个连通集合);
- 最终统计「独立的连通集合数量」,即为岛屿数量。
先把 "岛屿问题" 翻译成并查集的语言:
岛屿问题的核心是:统计网格中 "相互连通的陆地" 组成的独立集合数量(一个集合 = 一个岛屿)。
并查集的核心是:管理元素的连通性,统计独立集合的数量。
两者的核心诉求完全一致,我们只需要做一个 "翻译":
| 岛屿问题的概念 | 并查集的概念 | 具体对应方式 |
|---|---|---|
| 单个陆地单元格 (i,j) | 并查集中的 "元素" | 把二维坐标 (i,j) 映射成唯一的数字(比如 i*列数 + j),每个陆地就是一个元素 |
| 两个陆地连通(上下左右) | 两个元素属于 "同一个集合" | 用 union 操作把这两个元素合并到同一个集合 |
| 一个岛屿 | 一个 "独立的连通集合" | 并查集最终的 count(独立集合数)就是岛屿数 |
| 海洋单元格 | 无意义,不参与并查集操作 | 直接跳过 |
第二步:用 "小学生排队" 的例子理解(超通俗)
假设网格里的陆地是一群小学生,每个小学生初始时 "自己站一队"(对应并查集初始时每个陆地是独立集合):
- 规则:如果两个小学生是 "邻居"(上下左右相邻),就要站到同一队里(对应 union 合并);
- 最终:有多少 "独立的队伍",就有多少个岛屿。
举个具体的网格例子:
html
[1, 1]
[1, 0]对应小学生(陆地):
(0,0) → 编号 0,(0,1) → 编号 1,(1,0) → 编号 2(海洋 (1,1) 跳过)。
-
步骤 1:初始状态
每个小学生自己站一队,共 3 队(count=3):
plaintext队0:[0] 队1:[1] 队2:[2] -
步骤 2:处理邻居关系
(0,0) 和 (0,1) 是邻居 → 合并 0 和 1,队数减 1(count=2):
plaintext队0:[0,1] 队2:[2](0,0) 和 (1,0) 是邻居 → 合并 0 和 2,队数减 1(count=1):
plaintext队0:[0,1,2] -
步骤 3:最终结果
只剩 1 支队伍 → 对应 1 个岛屿(和实际一致)。
回到代码,拆解核心流程(对应上面的例子),用这个 2x2 的网格,一步步走并查集的代码逻辑:
- 初始化并查集
网格总单元格数 = 2*2=4 → 并查集 parent 数组长度 = 4(索引 0-3);
初始parent = [0,1,2,3](每个元素父节点是自己),rank = [1,1,1,1],count 先初始化为 0(后续统计陆地数)。 - 统计陆地数 + 合并连通陆地
遍历网格每个单元格:
(0,0) 是陆地 → 陆地数 = 1;检查右 (0,1)、下 (1,0) 都是陆地:
合并 0 和 1 → parent[1]=0,rank[0]=2,count(此时还没设初始值,先记合并次数);
合并 0 和 2 → parent[2]=0,rank[0] 仍为 2;
(0,1) 是陆地 → 陆地数 = 2;检查下 (1,1) 是海洋,无合并;
(1,0) 是陆地 → 陆地数 = 3;检查右 (1,1) 是海洋,无合并;
(1,1) 是海洋 → 跳过。 - 计算最终岛屿数
初始陆地数 = 3(每个陆地独立成队);
合并了 2 次 → 3-2=1 → 最终岛屿数 = 1。
对比 DFS/BFS,理解并查集的优势:【问题】"DFS/BFS 也能解决,为啥要用并查集?"
- DFS/BFS 是 "遍历式":找到一块陆地,就 "逛完" 整个岛屿并标记,统计逛的次数;
- 并查集是 "合并式":先把所有陆地拆成独立元素,再按连通关系合并,统计最终的独立集合数。
并查集的优势在于:
- 动态场景更友好:如果网格是 "动态的"(比如随时加 / 删陆地),DFS/BFS 需要重新遍历,而并查集只需新增 / 撤销合并操作;
- 批量处理连通性:如果需要多次查询 "两个陆地是否属于同一个岛屿",并查集的 find 操作是 O (1),比 DFS/BFS 反复遍历快得多。
代码如下:
js
var numIslands = function(grid) {
let m = grid.length;
let n = grid[0].length;
// 并查集
class UnionClass {
constructor(size) {
this.parent = new Array(size).fill(0).map((_, idx) => idx);
this.rank = new Array(size).fill(1);
this.count = 0;
}
// 查找根节点
find (x) {
if (this.parent[x] !== x) {
this.parent[x] = this.find(this.parent[x]);
}
return this.parent[x];
}
union(x, y) {
let rootX = this.find(x);
let rootY = this.find(y);
if (rootX === rootY) return;
if (this.rank[rootX] > this.rank[rootY]) {
this.parent[rootY] = rootX;
} else if (this.rank[rootX] < this.rank[rootY]) {
this.parent[rootX] = rootY;
} else {
this.parent[rootY] = rootX;
this.rank[rootX]++
}
this.count--;
}
setCount(num) {
this.count = num;
}
getCount() {
return this.count;
}
}
const getIndex = (i, j) => i * n + j;
let dirs = [[1, 0], [0, 1]];
let landCount = 0;
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (grid[i][j] === '1') {
landCount++;
}
}
}
let uf = new UnionClass(m * n);
uf.setCount(landCount);
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (grid[i][j] === '1') {
for (let [a, b] of dirs) {
let newX = a + i;
let newY = b + j;
if (newX < m && newY < n && grid[newX][newY] === '1') {
uf.union(getIndex(i, j), getIndex(newX, newY));
}
}
}
}
}
return uf.getCount()
};
};腐烂的橘子
题目描述
在给定的 m x n 网格 grid 中,每个单元格可以有以下三个值之一:
值 0 代表空单元格;
值 1 代表新鲜橘子;
值 2 代表腐烂的橘子。
每分钟,腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1 。
示例 1:
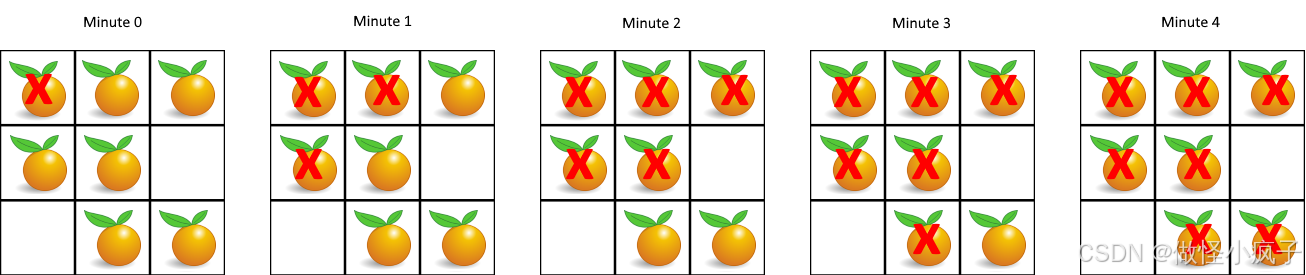
输入:grid = [[2,1,1],[1,1,0],[0,1,1]]
输出:4
示例 2:
输入:grid = [[2,1,1],[0,1,1],[1,0,1]]
输出:-1
解释:左下角的橘子(第 2 行, 第 0 列)永远不会腐烂,因为腐烂只会发生在 4 个方向上。
示例 3:
输入:grid = [[0,2]]
输出:0
解释:因为 0 分钟时已经没有新鲜橘子了,所以答案就是 0 。
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 10
grid[i][j] 仅为 0、1 或 2
求解
该题主要使用BFS,因为DFS是有优先级的,而BFS的一层是等价的。所以要么用多线程,要么就用BFS使得同一时刻的橘子在同一层使其等价,模拟同时进行感染,计算时间。
主要思路:使用 队列 存储当前的腐烂橘子,时间每过1,腐烂扩散;扩散的腐烂橘子 作为新的队列元素继续腐烂。
js
var orangesRotting = function(grid) {
// 广度搜索
let m = grid.length;
let n = grid[0].length;
let queue = [] // 腐烂的橘子
let fresh = 0; // 新鲜橘子数量
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (grid[i][j] === 1) fresh++;
if (grid[i][j] === 2) queue.push([i, j]);
}
}
let time = 0;
let dirs = [[-1, 0], [1, 0], [0, -1], [0, 1]];
while (queue.length > 0 && fresh > 0) {
let size = queue.length;
for (let i = 0; i < size; i++) {
let [x, y] = queue.shift();
for (let [a, b] of dirs) {
let newX = a + x;
let newY = b + y;
if (newX >= 0 && newX < m && newY >= 0 && newY < n && grid[newX][newY] === 1) {
grid[newX][newY] = 2;
fresh--;
queue.push([newX, newY]);
}
}
}
time++
}
return fresh === 0 ? time : -1;
};课程表
题目描述
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
例如,先修课程对 [0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:true
解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
示例 2:
输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
输出:false
解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
提示:
1 <= numCourses <= 2000
0 <= prerequisites.length <= 5000
prerequisites[i].length == 2
0 <= ai, bi < numCourses
prerequisites[i] 中的所有课程对 互不相同
求解
该题主要是使用 拓扑排序,主要针对有向无环图,只要所有的课程的依赖关系为有向无环图,那肯定能修完,要是不是,则有环,就返回false;
经典实现:Kahn 算法(入度表 + 队列,贪心策略)
核心思想:
- 先找到所有入度为 0 的节点,作为排序起点;
- 把起点加入结果,然后 "移除" 该节点的所有出边(即减少其邻接节点的入度);
- 重复步骤 1-2,直到所有节点都加入结果(成功),或图中还有节点但无入度为 0 的节点(失败,说明有环)。
代码:
js
var canFinish = function(numCourses, prerequisites) {
// 邻接表 + 入度表
let adj = new Array(numCourses).fill(0).map(() => []);
let inDress = new Array(numCourses).fill(0);
for (let [u, v] of prerequisites) {
// u ⬅ v
adj[v].push(u);
inDress[u]++;
}
let queue = []; // 队列:存储 入度为0的课程
for (let i = 0; i < inDress.length; i++) {
if (inDress[i] === 0) queue.push(i);
}
let count = 0;
while(queue.length > 0) {
let v = queue.shift();
count++;
// 删掉所有出边
for (let u of adj[v]) {
inDress[u]--;
if (inDress[u] === 0) queue.push(u);
}
}
return count === numCourses;
};图论相关知识
一、图论核心基础概念
1.图的分类(定义 + 场景)
| 类型 | 定义 | 典型场景 |
|---|---|---|
| 无向图 | 边无方向,A-B 等价于 B-A | 社交网络(好友关系)、岛屿问题 |
| 有向图 | 边有方向,A→B 不等价于 B→A | 任务依赖、课程表(先修课) |
| 加权图 | 边带权重(数值),如 A-B (5) 表示边权重为 5 | 最短路径(网络延迟时间) |
| 有向无环图 | (DAG)有向图中不存在环 | 拓扑排序、动态规划(DAG 最长路) |
2.图的存储方式
(1)邻接表(推荐,稀疏图首选)
定义:用数组 / 哈希表 存储每个顶点的邻接顶点列表,空间复杂度 O ( V + E ) O(V+E) O(V+E)(V = 顶点数,E = 边数)。代码实现:
javascript
// 无向图邻接表(顶点 0~n-1)
function buildUndirectedGraph(n, edges) {
const adj = new Array(n).fill(0).map(() => []);
for (const [u, v] of edges) {
adj[u].push(v);
adj[v].push(u); // 无向图:双向添加
}
return adj;
}
// 有向加权图邻接表
function buildDirectedWeightedGraph(n, edges) {
const adj = new Array(n).fill(0).map(() => []);
for (const [u, v, w] of edges) {
adj[u].push([v, w]); // 存储 [邻接顶点, 权重]
}
return adj;
}
// 示例:无向图 edges = [[0,1],[1,2],[0,2]]
const adj = buildUndirectedGraph(3, [[0,1],[1,2],[0,2]]);
console.log(adj); // [[1,2], [0,2], [1,0]](2)邻接矩阵定义:
二维数组 graph[i][j] 表示顶点 i 到 j 是否有边(无权图:0/1;加权图:权重 /∞),空间复杂度 O ( V 2 ) O(V^2) O(V2)(稠密图首选)。代码实现:
javascript
// 无向无权图邻接矩阵
function buildAdjMatrix(n, edges) {
const matrix = new Array(n).fill(0).map(() => new Array(n).fill(0));
for (const [u, v] of edges) {
matrix[u][v] = 1;
matrix[v][u] = 1; // 无向图双向置1
}
return matrix;
}
// 示例:edges = [[0,1],[1,2]]
const matrix = buildAdjMatrix(3, [[0,1],[1,2]]);
console.log(matrix);
// [[0,1,0], [1,0,1], [0,1,0]]3.图的核心术语
- 度:无向图中顶点的边数(如邻接表中 adj[i].length);
- 入度 / 出度:有向图中,入度 = 指向该顶点的边数,出度 = 该顶点指向其他的边数;
- 连通分量 :无向图中最大连通子图(如岛屿数量就是连通分量数);
- 强连通分量:有向图中,子图内任意两点互相可达。
二、核心图论算法(定义 + 完整实现)
1.图的遍历:DFS(深度优先搜索)
(1)定义
从起点出发,优先遍历「当前顶点的邻接顶点」,直到无法前进后回溯,本质是 "一条路走到黑",可用递归 / 栈实现。
(2)适用场景
路径查找、环检测、连通分量统计(如岛屿数量)。
(3)代码实现(递归版,无向图遍历)
javascript
// 遍历无向图,统计连通分量(岛屿数量核心逻辑)
function dfsTraverse(adj) {
const n = adj.length;
const visited = new Array(n).fill(false); // 标记是否访问过
let componentCount = 0; // 连通分量数
// 递归DFS
const dfs = (u) => {
visited[u] = true; // 标记已访问
for (const v of adj[u]) { // 遍历所有邻接顶点
if (!visited[v]) {
dfs(v); // 递归访问未访问的邻接顶点
}
}
};
// 遍历所有顶点(处理非连通图)
for (let i = 0; i < n; i++) {
if (!visited[i]) {
componentCount++;
dfs(i);
}
}
return componentCount;
}
// 示例:adj = [[1,2], [0,2], [1,0]]
console.log(dfsTraverse([[1,2], [0,2], [1,0]])); // 输出 1(全连通)2.图的遍历:BFS(广度优先搜索)
(1)定义
从起点出发,优先遍历「当前顶点的所有邻接顶点」,再遍历邻接顶点的邻接顶点,本质是 "层层扩散",用队列实现。
(2)适用场景
无权图最短路径、层次遍历(如腐烂的橘子)、拓扑排序(Kahn 算法)。
(3)代码实现(队列版,腐烂的橘子核心逻辑)
javascript
// BFS遍历,模拟扩散过程(腐烂的橘子)
function bfsTraverse(grid) {
const m = grid.length, n = grid[0].length;
const queue = []; // 存储待扩散的节点(行、列)
let fresh = 0; // 新鲜橘子数量
const dirs = [[-1,0],[1,0],[0,-1],[0,1]]; // 上下左右
// 初始化:将所有腐烂橘子入队,统计新鲜橘子
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (grid[i][j] === 2) queue.push([i, j]);
if (grid[i][j] === 1) fresh++;
}
}
let time = 0; // 扩散时间
// BFS核心
while (queue.length > 0 && fresh > 0) {
const size = queue.length; // 当前层节点数(控制层次)
for (let i = 0; i < size; i++) {
const [x, y] = queue.shift();
// 遍历四个方向
for (const [dx, dy] of dirs) {
const nx = x + dx, ny = y + dy;
if (nx >=0 && nx < m && ny >=0 && ny < n && grid[nx][ny] === 1) {
grid[nx][ny] = 2; // 腐烂
fresh--;
queue.push([nx, ny]);
}
}
}
time++; // 一层遍历完,时间+1
}
return fresh === 0 ? time : -1; // 全部腐烂返回时间,否则-1
}
// 示例:grid = [[2,1,1],[1,1,0],[0,1,1]]
console.log(bfsTraverse([[2,1,1],[1,1,0],[0,1,1]])); // 输出 43.拓扑排序(针对 DAG)
(1)定义
将有向无环图(DAG)的顶点排序,使得所有有向边 u→v 中,u 排在 v 前面,解决 "依赖顺序" 问题(如课程表)。
(2)常用实现:Kahn 算法(入度表 + BFS)
核心逻辑:
- 统计所有顶点的入度;
- 入度为 0 的顶点入队(无依赖,可优先处理);
- 出队时删除该顶点的所有出边(邻接顶点入度 - 1),入度为 0 则入队;
- 最终若排序结果长度 = 顶点数,说明无环,否则有环。
(3)代码实现(课程表核心逻辑)
javascript
// 拓扑排序:判断是否可以完成所有课程(课程表 I)
function canFinish(numCourses, prerequisites) {
const adj = new Array(numCourses).fill(0).map(() => []); // 邻接表
const inDegree = new Array(numCourses).fill(0); // 入度表
// 构建邻接表+入度表
for (const [v, u] of prerequisites) { // u→v(修v前先修u)
adj[u].push(v);
inDegree[v]++;
}
const queue = [];
// 入度为0的课程入队
for (let i = 0; i < numCourses; i++) {
if (inDegree[i] === 0) queue.push(i);
}
let count = 0; // 已完成的课程数
while (queue.length > 0) {
const u = queue.shift();
count++;
// 删除u的所有出边
for (const v of adj[u]) {
inDegree[v]--;
if (inDegree[v] === 0) queue.push(v);
}
}
return count === numCourses; // 全部完成则无环
}
// 示例:numCourses=2, prerequisites=[[1,0]]
console.log(canFinish(2, [[1,0]])); // 输出 true(可完成)
// 示例:numCourses=2, prerequisites=[[1,0],[0,1]]
console.log(canFinish(2, [[1,0],[0,1]])); // 输出 false(有环)4.并查集(Union-Find)
(1)定义
一种高效管理「连通性」的数据结构,支持两个核心操作:
find(x):查找 x 的根节点(路径压缩优化);union(x,y):合并 x 和 y 所在集合(按秩合并优化)。
(2)适用场景
连通分量统计、冗余连接、岛屿数量(替代 DFS/BFS)。
(3)代码实现(带路径压缩 + 按秩合并)
javascript
class UnionFind {
constructor(n) {
this.parent = new Array(n).fill(0).map((_, idx) => idx); // 父节点初始指向自己
this.rank = new Array(n).fill(1); // 秩(树的高度)
}
// 查找根节点(路径压缩:直接指向根,降低树高)
find(x) {
if (this.parent[x] !== x) {
this.parent[x] = this.find(this.parent[x]); // 递归压缩
}
return this.parent[x];
}
// 合并两个集合(按秩合并:矮树挂到高树下)
union(x, y) {
let rootX = this.find(x);
let rootY = this.find(y);
if (rootX === rootY) return false; // 已连通,合并失败
// 按秩合并
if (this.rank[rootX] > this.rank[rootY]) {
this.parent[rootY] = rootX;
} else if (this.rank[rootX] < this.rank[rootY]) {
this.parent[rootX] = rootY;
} else {
this.parent[rootY] = rootX;
this.rank[rootX]++;
}
return true;
}
}
// 示例:统计连通分量(岛屿数量)
function countComponents(n, edges) {
const uf = new UnionFind(n);
for (const [u, v] of edges) {
uf.union(u, v);
}
// 统计根节点数量(连通分量数)
const roots = new Set();
for (let i = 0; i < n; i++) {
roots.add(uf.find(i));
}
return roots.size;
}
// 示例:n=5, edges=[[0,1],[1,2],[3,4]]
console.log(countComponents(5, [[0,1],[1,2],[3,4]])); // 输出 2(两个连通分量)