算法题
题目1:14. 最长公共前缀 - 力扣(LeetCode)
题目分析
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串
""。
题目示例
示例 1:
输入:strs = ["flower","flow","flight"] 输出:"fl"示例 2:
输入:strs = ["dog","racecar","car"] 输出:"" 解释:输入不存在公共前缀。提示:
1 <= strs.length <= 2000 <= strs[i].length <= 200strs[i]如果非空,则仅由小写英文字母组成
算法原理
解法1:字符串两两比较
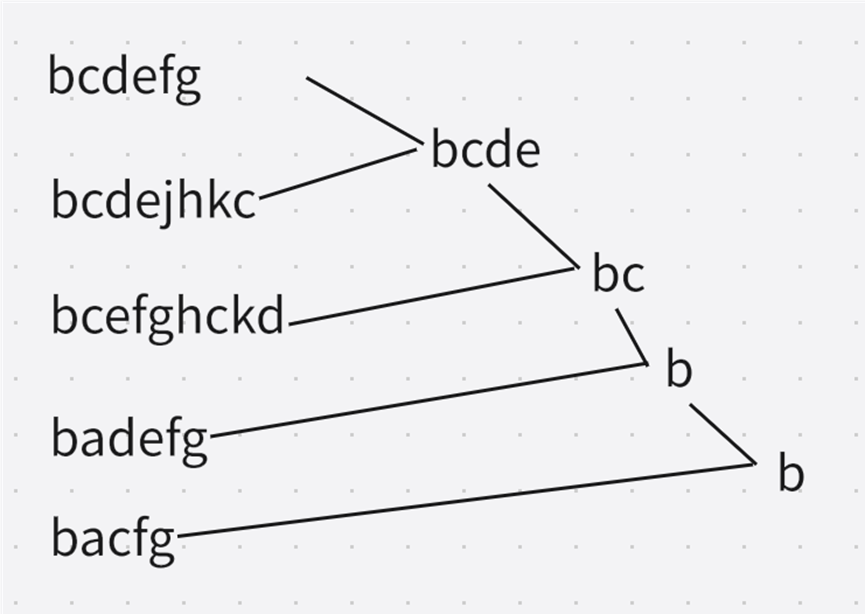
如何找到两个字符串的前缀,使用指针。就相当于获取两个字符串相等的部分。
代码实现
cpp
class Solution {
public:
// 求两个字符串的前缀
string PrefixStr(const string& str1, const string& str2)
{
int i = 0;
// 避免下标越界
for(; i < str1.length() && i < str2.length(); i++)
{
if(str1[i] != str2[i]) { break; }
}
// 从0开始,截取i个字符
return str1.substr(0, i);
}
string longestCommonPrefix(vector<string>& strs) {
// 解法1:字符串两两比较
string ret = strs[0];
for(int i = 1; i < strs.size(); i++)
{
ret = PrefixStr(ret, strs[i]);
}
return ret;
}
};解法2:统一比较
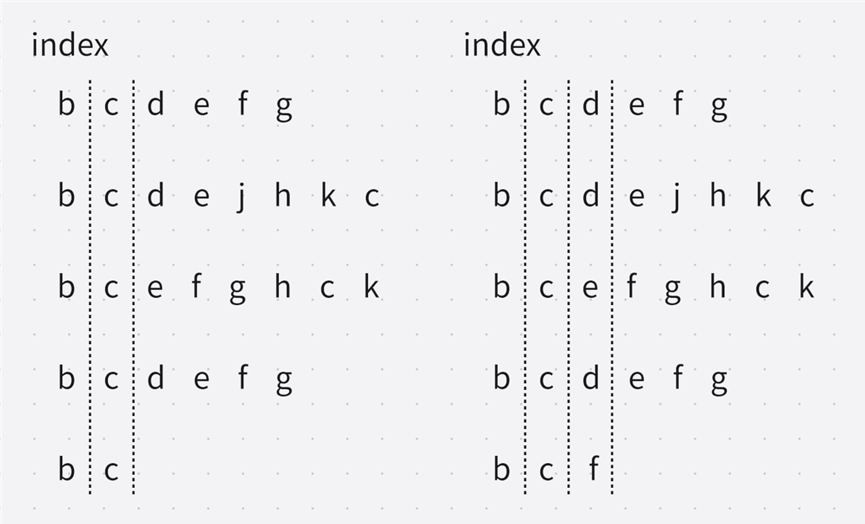
当某个字符串的下标越界了/遍历到的字符不相等时,停止遍历。
代码实现
cpp
class Solution {
public:
string longestCommonPrefix(vector<string>& strs) {
// 解法2:统一比较
// 以第一个字符串的长度为基准
for(int i = 0; i < strs[0].length(); i++)
{
// 进行比较的基准值就是第一个字符串的第i个字符
char privot = strs[0][i];
// 遍历strs中的每一个字符串
for(int j = 1; j < strs.size(); j++)
{
// 当某个字符串的字符不等于基准值时,返回
// 或者i的大小等于字符串的长度,返回
if(strs[j].length() == i || strs[j][i] != privot) { return strs[0].substr(0, i); }
}
}
// 如果遍历比较所有字符串,仍然没有结果,返回第一个字符串
return strs[0];
}
};题目2:5. 最长回文子串 - 力扣(LeetCode)
题目分析
给你一个字符串
s,找到s中最长的 回文 子串。
如果字符串向前和向后读都相同,则它满足 回文性。
题目示例
示例 1:
输入:s = "babad" 输出:"bab" 解释:"aba" 同样是符合题意的答案。示例 2:
输入:s = "cbbd" 输出:"bb"提示:
1 <= s.length <= 1000s仅由数字和英文字母组成
算法原理
解法:中心扩展算法
中心扩展算法就是暴力解法,只不过是借助了回文子串的特性。一般的暴力枚举,固定一个字符,向后遍历,判断子串是否是回文子串,时间复杂度为O(N^3)。
中心扩展算法:
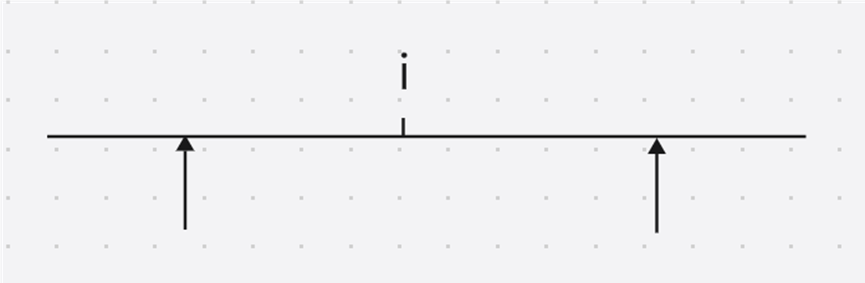
以 i 为中心,向左向右枚举观察能扩展到哪?为什么要这么做?因为这就是回文串的特性,字符串向前和向后读都相同。当确定好中心点后,定义两个指针分别从中心点开始向左向右移动,若两指针指向位置的字符相等时,继续移动,若不想等,那么这两个指针指向的区域就是回文串。这样枚举出来的回文子串都是奇数长度的,但是有可能最终结果是偶数,这样一来需要优化。
在两个指针开始指向中心点时,先找奇数最长的回文子串,再找偶数最长的子串。
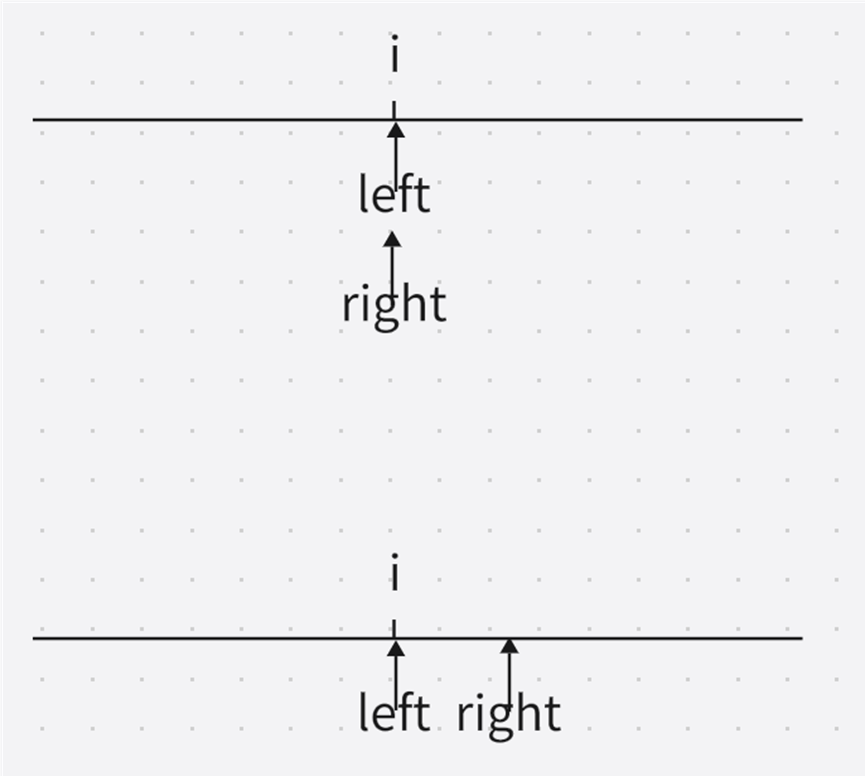
算法步骤
固定一个中心点
从中心点开始,向两边扩展(注意:奇数长度以及偶数长度都需要考虑)
奇数:left和right指针指向中心点位置;偶数:left 指向中心点位置,right 指向中心点右边的位置
注意:题目最终的结果是返回最长的回文子串,因此需要记录子串的起始位置与长度
代码实现
cpp
class Solution {
public:
string longestPalindrome(string s) {
int len = s.length();
// 记录子串的起始位置和最长回文串的长度
int flag = -1, maxlen = -1;
// 找中心点
for(int mid = 0; mid < len; mid++)
{
// 定义两个指针
int left = mid, right = mid; // 指向的相同的位置
// 先找奇数长度
while(left >= 0 && right < len && s[left] == s[right])
{
left--;
right++;
}
// 记录当前子串的起始位置与长度
if(right - left - 1 > maxlen)
{
maxlen = right - left - 1;
flag = left + 1;
}
// 再找偶数长度
left = mid, right = mid + 1; // 错开指向
while(left >= 0 && right < len && s[left] == s[right])
{
left--;
right++;
}
// 记录当前子串的起始位置与长度
if(right - left - 1 > maxlen)
{
maxlen = right - left - 1;
flag = left + 1;
}
}
return s.substr(flag, maxlen);
}
};题目3:67. 二进制求和 - 力扣(LeetCode)
题目分析
给你两个二进制字符串
a和b,以二进制字符串的形式返回它们的和。
这就是一个高精度加法的题目。二进制运算:逢二进一
题目示例
示例 1:
输入:a = "11", b = "1" 输出:"100"示例 2:
输入:a = "1010", b = "1011" 输出:"10101"提示:
1 <= a.length, b.length <= 104a和b仅由字符'0'或'1'组成- 字符串如果不是
"0",就不含前导零
算法原理
解法:模拟列竖式运算

代码实现
cpp
class Solution {
public:
string addBinary(string a, string b) {
// 相加是从末尾开始的,因此指针的初始指向字符串的末尾
int cur1 = a.length() - 1, cur2 = b.length() - 1;
int tmp = 0; // 记录相加的结果
string ret; // 返回值
// 循环 只要字符串a/b没有加完,或者还有进位
while(cur1 >= 0 || cur2 >= 0 || tmp)
{
if(cur1 >= 0) { tmp += a[cur1--] - '0'; }
if(cur2 >= 0) { tmp += b[cur2--] - '0'; }
ret += tmp % 2 + '0';
tmp /= 2; // 进位
}
// 存的时候是倒着存,返回要正着返回
reverse(ret.begin(), ret.end());
return ret;
}
};题目4:43. 字符串相乘 - 力扣(LeetCode)
题目分析
给定两个以字符串形式表示的非负整数
num1和num2,返回num1和num2的乘积,它们的乘积也表示为字符串形式。**注意:**不能使用任何内置的 BigInteger 库或直接将输入转换为整数。
题目示例
示例 1:
输入: num1 = "2", num2 = "3" 输出: "6"示例 2:
输入: num1 = "123", num2 = "456" 输出: "56088"提示:
1 <= num1.length, num2.length <= 200num1和num2只能由数字组成。num1和num2都不包含任何前导零,除了数字0本身。
算法原理
解法1:模拟列竖式运算
两个字符串 num1 和 num2,从 num1 中取末尾字符与 num2 中的每个字符相乘,使用变量 tmp 记录相乘的结果乘,然后将结果与返回值 ret 累加在一起。
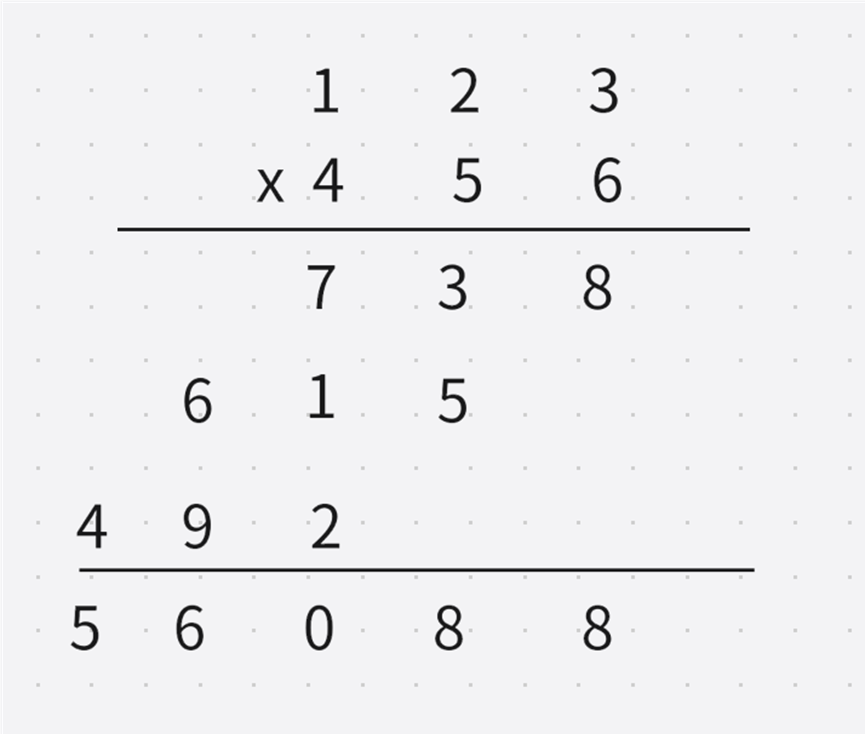
细节处理:
高位相乘的时候,需要补上'0',与738相加的不是615,而是6150。
对于高精度的题目,首先需要将源字符串逆序,上一道题目没有逆序是因为只是简单的加法。先将 num1 逆序,那么"123"就是"321",将 num2 中的字符5与"321"相乘,5的下标为1,因此记录相乘的结果 tmp 先加上一个字符'0',接下来将相乘时的结果尾插在 tmp 中,最终计算的结果再逆序返回即可
处理前导'0',如果 num1 和 num2 中有个字符串就是"0",需要特殊处理
解法1的思路很简单,但是代码不容易写,推荐使用解法2。
解法2:无进位相乘然后相加,最后处理进位
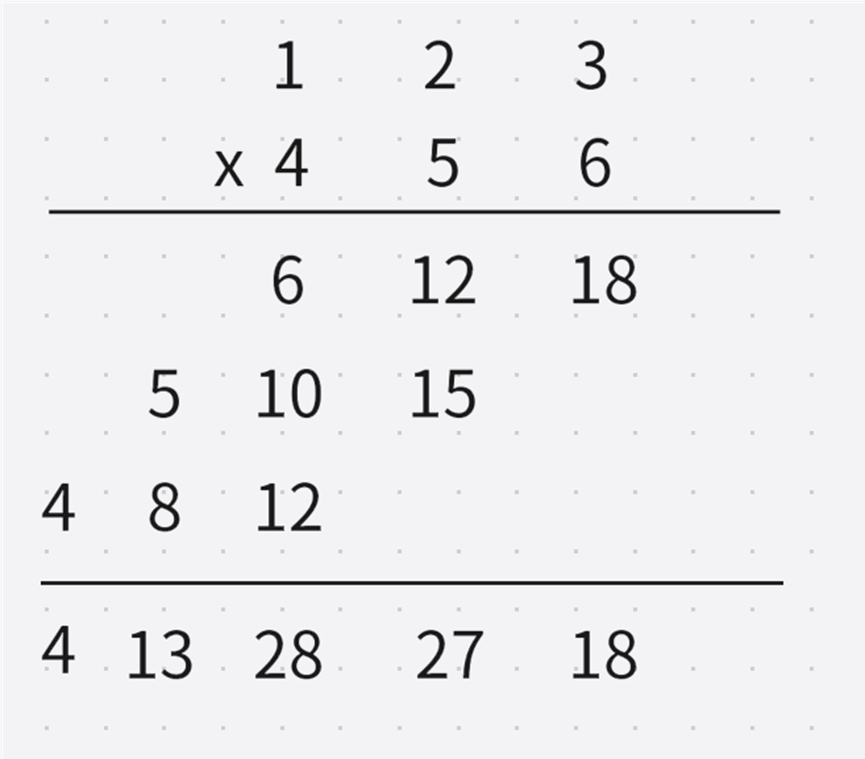
得到这么一个数组之后,再处理进位。
处理18,进位1,剩8
处理27,27加上进位的1,进位2,剩8
处理28,28加上进位的2,进位3,剩0
处理13,13加上进位的3,进位1,剩6
处理4,4加上进位的1,无进位,剩5
最终结果:56088
为什么会得到正确的结果?两个方法都要进位,只是进位的时机不一样。
依旧先将字符串逆序,解法1是使用字符串记录相乘的结果,这里使用数组记录相乘的结果,数组开多大,若 num1 的长度为 m,num2 的长度为 n,那么两数字字符串相乘结果的长度一定是m+n-1。

0下标和0下标的字符相乘,结果存到0下标位置
0下标和1下标的字符相乘,结果存到1下标位置
0下标和2下标的字符相乘,结果存到2下标位置
1下标和0下标的字符相乘,结果存到1下标位置
1下标和1下标的字符相乘,结果存到2下标位置
1下标和2下标的字符相乘,结果存到3下标位置
2下标和0下标的字符相乘,结果存到2下标位置
2下标和1下标的字符相乘,结果存到3下标位置
2下标和2下标的字符相乘,结果存到4下标位置
m下标和n下标的字符相乘,结果存到m+n下标位置
得到数组之后,接下来处理进位,就是模拟相加。此外需要处理前导'0'问题。
代码实现
cpp
class Solution {
public:
string multiply(string num1, string num2) {
// 求出两字符串的长度,方便创建数组tmp
int m = num1.length(), n = num2.length();
// 处理前导'0'问题 (字符串单独为0)
if((m == 1 && num1[0] == '0') || (n == 1 && num2[0] == '0')) { return "0"; }
// 逆序两个字符串
reverse(num1.begin(), num1.end());
reverse(num2.begin(), num2.end());
// 创建一个数组存储字符相乘的结果
vector<int> tmp(m + n - 1); // 初始化为0
// 无进位相乘,再相加
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
int num = (num1[i] - '0') * (num2[j] - '0'); // 字符相乘的结果
// i下标和j下标的字符相乘,结果与i+j下标位置存储的元素相加
tmp[i+j] += num;
}
}
string ret; // 返回值
int temp = 0, i = 0; // 存储相加的结果
// 处理返回值
while(i < tmp.size() || temp != 0)
{
if(i < tmp.size())
{
temp = tmp[i++] + temp;
}
ret += (temp%10 + '0');
temp /= 10; // 进位
}
// 处理前导'0'问题
// 要保存最后的'0',因此判断条件有字符串的长度要大于1
//while(ret.length() > 1 && ret.back() == '0') { ret.pop_back(); }
// 逆序
reverse(ret.begin(), ret.end());
return ret;
}
};