数据结构------平衡二叉树
平衡二叉树定义
"平衡因子(Balanced Factor,简称BF)": B F ( T ) = h L − h R BF(T)=h_L-h_R BF(T)=hL−hR,其中 h L h_L hL和 h R h_R hR分别为T的左、右子树的高度。
平衡二叉树(Balanced Binary Tree),是空树,或者 任一结点左、右子树高度差的绝对值不超过1,即 ∣ B F ( T ) < = 1 ∣ |BF(T)<=1| ∣BF(T)<=1∣
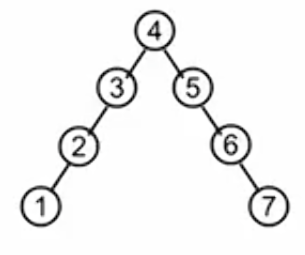
上图就不是平衡二叉树
AVL树
AVL 树(Adelson-Velsky and Landis Tree)是一种 自平衡的二叉搜索树,对任意结点,其左右子树的高度差(平衡因子)绝对值不超过 1。
AVL= 平衡二叉树+二叉搜索(排序)树
AVL = 三位苏联学者的名字首字母
Adelson-Velsky
Velsky
Landis
📌 这是世界上第一种被提出的平衡二叉搜索树(1962 年)。
性质:给定结点数为n的AVL树的最大高度为 O ( l o g 2 n ) O(log_2n) O(log2n)
AVL树的调整
当给一个AVL树插入一个新结点后,可能会出现不平衡的状态。此时,就需要进行旋转来调整,恢复道平衡的状态。
RR 右单旋
插入新结点后,
A是问题出现的结点,它的平衡因子变成了-2,由此出现了不平衡。
E是插入新结点的父结点。E在A的右子树的右结点,所以叫RR插入,需要进行RR旋转(右单旋)
F是新插入的结点,F的左右没有影响,主要是看E和A的位置关系。
D是这个变换中,唯一被更换父节点的结点
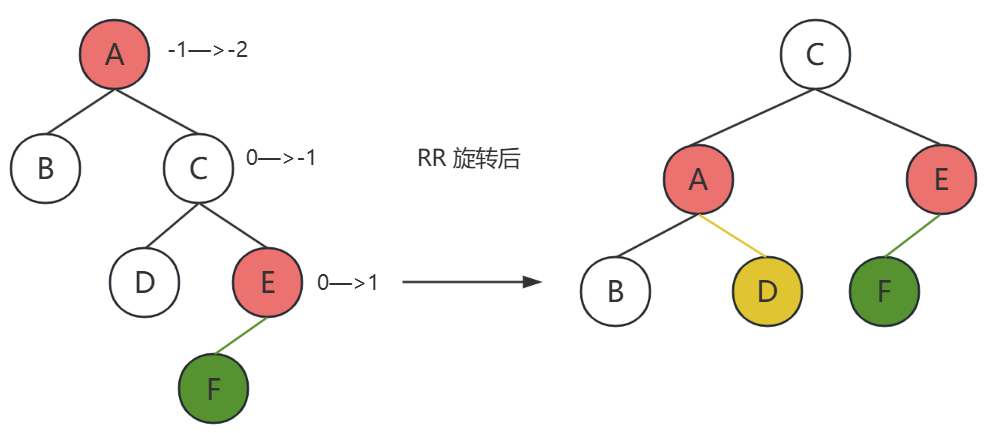
上图是AVL树RR旋转的最下端截取,因为AVL插入引起的不平衡一定是对最下端造成的影响,上层结点的平衡因子都被+1,只要解决这3层,上层的问题都被解决。
LL 左单旋
插入新结点后,
A是问题出现的结点,它的平衡因子变成了2,由此出现了不平衡。
D是新结点插入的结点。D在A的左子树的左结点,所以叫LL插入,需要进行LL旋转(左单旋)
F是新插入的结点
E是这个变换中,唯一被更换父节点的结点
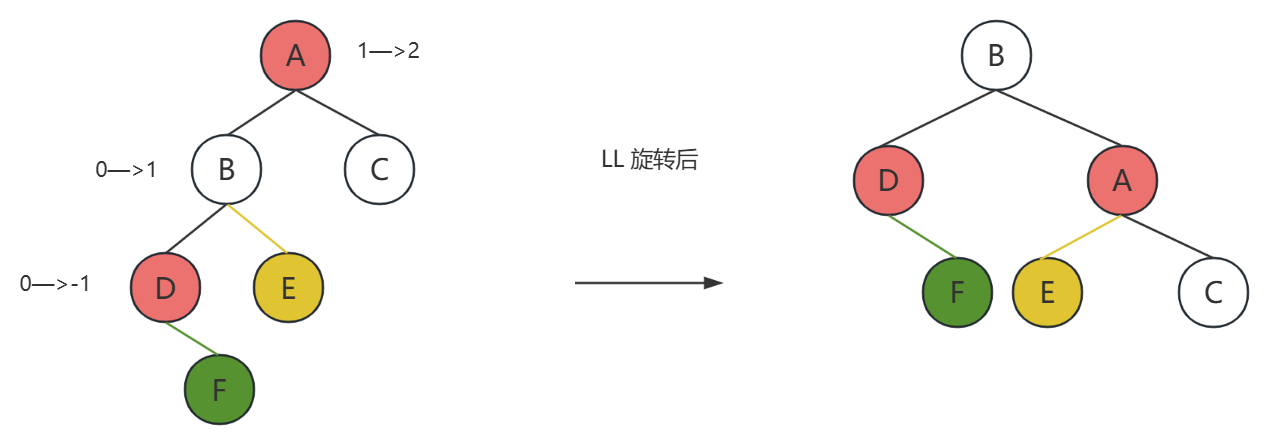
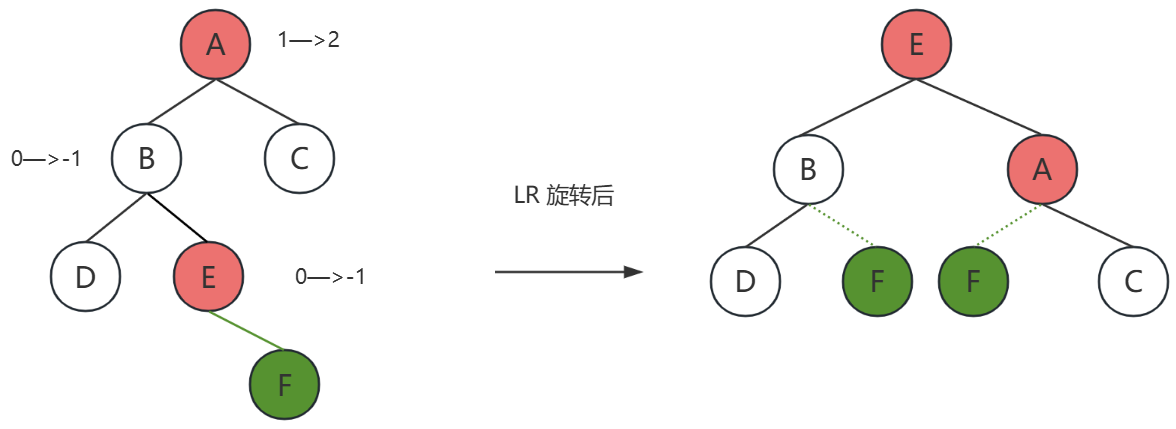
LR 旋转
插入新结点后,
A是问题出现的结点,它的平衡因子变成了2,由此出现了不平衡。
E是新结点插入的结点。E在A的左子树的右结点,所以叫LR插入,需要进行LR旋转
F是新插入的结点
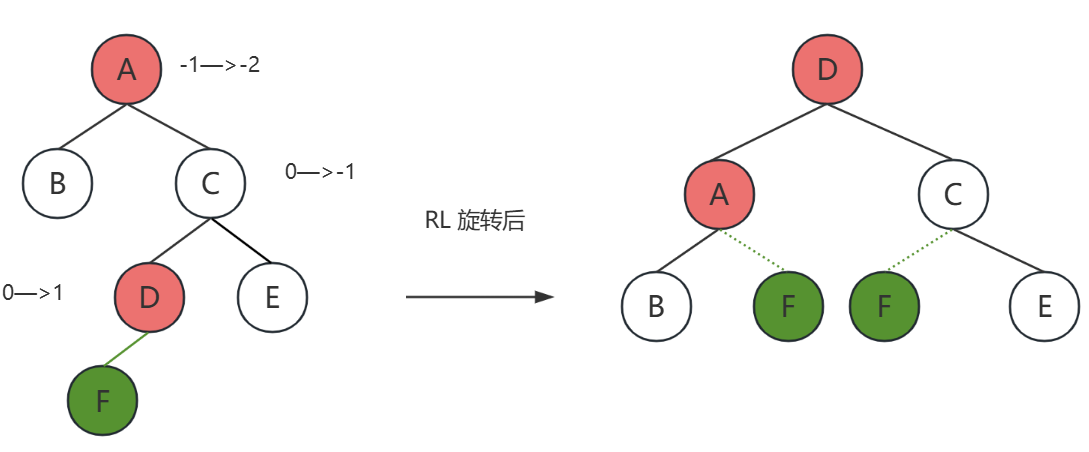
RL 旋转
插入新结点后,
A是问题出现的结点,它的平衡因子变成了-2,由此出现了不平衡。
D是新结点插入的结点。D在A的右子树的左结点,所以叫RL插入,需要进行RL旋转
F是新插入的结点
总结
RR和LL旋转,都是中间提起。中间结点多余原有的子树,直接接到原根节点上。其余结构保持不变。
RL和LR旋转,都是最后一个结点当根节点,其余上层两个分别作为左右子树。新增结点,在左右子树根结点上两个哪个都可以。其余结点结构保持不变。