前言
最后一题有点难嗷~~~
A - o-padding
大致题意
给你个字符串 SSS,然后需要你把他的长度变成 NNN,也就是用 o 这个字母补充在 SSS 的前面,需要几个补几个。
思路
计算 NNN 和 S.size()S.size()S.size() 的差值,然后在一开始的时候输出对应个数的 o ,然后再输出一遍 SSS。
代码
cpp
#include <bits/stdc++.h>
using namespace std;
int main()
{
int len;
cin >> len;
string s;
cin >> s;
for (int i = 1; i <= len - s.size(); i++)
cout << 'o';
cout << s;
return 0;
}B - Magic Square
大致题意
给定一个不小于 333 的奇数 NNN。
现有一个 NNN 行 NNN 列的方格矩阵,所有格子初始时均为空。请按照以下步骤,在矩阵的每个格子中填入整数。设 (i,j)(i, j)(i,j) 表示从顶部数第 i+1i+1i+1 行、从左侧数第 j+1j+1j+1 列的格子,其中 (0≤i<N, 0≤j<N)(0 \le i < N,\ 0 \le j < N)(0≤i<N, 0≤j<N)。
- 首先,在格子 (0,n−12)(0, \frac{n - 1}{2})(0,2n−1) 中填入数字 111。
- 重复执行以下操作 N2−1N^2-1N2−1 次:设 (r,c)(r,c)(r,c) 为上一个填入数字的格子,k 为该格子中填入的数字。检查格子 ((r−1)mod N,(c+1)mod N)((r-1) \mod N, (c+1) \mod N)((r−1)modN,(c+1)modN) 是否为空:若为空,则在该格子中填入 k+1k+1k+1;若不为空,则在格子 ((r+1)mod N,c)((r+1)\mod N,c)((r+1)modN,c) 中填入 k+1k+1k+1。注:xmod Nx \mod NxmodN 表示 x 除以 N 所得的余数。
请你求出最终矩阵中每个格子里填入的整数。可以证明,矩阵中的每个格子都会被恰好填入一个整数。
解题思路
按照题目中给出流程进行操作即可,具体看代码。
代码
cpp
#include <bits/stdc++.h>
using namespace std;
const int maxn = 105;
int n, ans[maxn][maxn];
int main()
{
cin >> n;
int x = 0, y = n / 2, cnt = 2;
ans[x][y] = 1;
while (1)
{
int X = (x - 1 + n) % n, Y = (y + 1) % n;
if (ans[X][Y] != 0)
x = (x + 1) % n;
else
x = X, y = Y;
if (ans[x][y] != 0)
break;
ans[x][y] = cnt++;
}
for (int i = 0; i < n; i++, cout << '\n')
for (int j = 0; j < n; j++)
cout << ans[i][j] << ' ';
return 0;
}C - 2x2 Placing
大致题意
给定一个 N×NN \times NN×N 的方格矩阵,设 (i,j)(i,j)(i,j) 表示从上往下数第 iii 行、从左往右数第 jjj 列的格子,矩阵初始为空。
你需要执行 MMM 次操作,第 iii 次操作规则如下:
- 尝试放置一个 2×2 的方块 ,方块的左上角为格子 (Ri,Ci)(R_i,C_i)(Ri,Ci);
- 放置条件:这个 2×2 方块覆盖的 4 个格子 {(Ri,Ci),(Ri+1,Ci),(Ri,Ci+1),(Ri+1,Ci+1)}\{(R_i,C_i), (R_i+1,C_i), (R_i,C_i+1), (R_i+1,C_i+1)\}{(Ri,Ci),(Ri+1,Ci),(Ri,Ci+1),(Ri+1,Ci+1)},不能与任何已放置的方块重叠;
- 若满足条件则放置,否则不进行任何操作。
完成所有 MMM 次操作后,求最终矩阵上成功放置的方块总数 。
解题思路
虽然 NNN 非常的大,但是方块的数量很小,我们可以使用 map 来维护所有已经被占用的块的信息。每次输入一个方块的信息,我们就从 map 里面寻找这些块,找到了就说明不合法,反之为合法,最后记得把新加入的块维护到 map 里面。
代码
cpp
#include <bits/stdc++.h>
using namespace std;
map<pair<int, int>, int> g;
int X[4] = {0, 1, 0, 1}, Y[4] = {0, 0, 1, 1};
int main()
{
int n, m, ans = 0;
cin >> n >> m;
while (m--)
{
int x, y;
cin >> x >> y;
if (x >= 1 && x < n && y >= 1 && y < n)
{
int f = 1;
for (int i = 0; i < 4; i++)
{
pair<int, int> tmp = {x + X[i], y + Y[i]};
if (g[tmp] != 0)
f = 0;
}
if (f)
for (int i = 0; i < 4; i++)
{
pair<int, int> tmp = {x + X[i], y + Y[i]};
g[tmp] = 1;
}
ans += f;
}
}
cout << ans;
return 0;
}D - Teleport Maze
大致题意
现有一个由 HHH 行 WWW 列方格组成的迷宫。设 (i,j)(i,j)(i,j) 表示从上往下数第 iii 行、从左往右数第 jjj 列 的格子,每个格子的类型由字符 Si,jS_{i,j}Si,j 表示,具体含义如下:
.:空单元格#:障碍物单元格- 小写英文字母(a-z):传送单元格
在迷宫中,你可以任意次数、任意顺序执行以下两种操作:
- 行走 :从当前格子向上下左右四个方向之一移动一格。不能移动到障碍物格子或迷宫之外。
- 传送 :当处于某传送单元格时,可直接移动到任意一个写有相同字母的传送单元格。
请判断能否从起点 (1,1)(1,1)(1,1) 移动到终点 (H,W)(H,W)(H,W)。若可以,求出所需的最少操作次数 。
解题思路
一眼 BFS,首先对于所有空地而言,我们可以使用传统的方法进行遍历,枚举四个方向 x 和 y 值的变化,寻找出下一个点,用一个 dis 值来标记距离。因为是 BFS,越早到达肯定越近,所以一个点只需要被遍历一次即可,不过要检查一下是不是障碍物或者越界。
其次就是关于传送,我们发现只要我们到达了一个小写字母的格子,其他相同的小写字母格子就全部能被遍历了,所以假设我们到达了一个小写字母格子,假设距离为 KKK,那么我们就把和他所有相同的格子都用 dis 数组标记为 K+1K + 1K+1,然后丢到队列里面方便搜索,后面就不需要再管这些格子了。
代码
cpp
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1005;
int n, m, dis[maxn][maxn], X[4] = {-1, 0, 1, 0}, Y[4] = {0, -1, 0, 1}, vis[30];
char g[maxn][maxn];
vector<pair<int, int>> edge[30];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
{
cin >> g[i][j];
dis[i][j] = -1;
if (g[i][j] >= 'a' && g[i][j] <= 'z')
edge[g[i][j] - 'a' + 1].push_back({i, j});
}
if (g[1][1] == '#')
{
cout << -1;
return 0;
}
queue<pair<int, int>> q;
dis[1][1] = 0;
q.push({1, 1});
while (!q.empty())
{
auto [x, y] = q.front();
q.pop();
for (int i = 0; i < 4; i++)
{
int vx = x + X[i], vy = y + Y[i];
if (vx >= 1 && vx <= n && vy >= 1 && vy <= m && dis[vx][vy] == -1 && g[vx][vy] != '#')
{
dis[vx][vy] = dis[x][y] + 1;
q.push({vx, vy});
}
}
if (g[x][y] >= 'a' && g[x][y] <= 'z')
{
int id = g[x][y] - 'a' + 1;
if (vis[id])
continue;
vis[id] = 1;
for (int i = 0; i < edge[id].size(); i++)
{
auto [vx, vy] = edge[id][i];
if (dis[vx][vy] == -1)
{
dis[vx][vy] = dis[x][y] + 1;
q.push({vx, vy});
}
}
}
}
cout << dis[n][m];
return 0;
}E - Minimum Swap
大致题意
给定一个长度为 NNN 的整数序列 PPP,该序列是 (1,2,...,N)(1,2,\dots,N)(1,2,...,N) 的一个排列 ,且保证 PPP 不等于 (1,2,...,N)(1,2,\dots,N)(1,2,...,N)。
你可以执行零次或多次 以下操作,目标是将 PPP 变为有序序列 (1,2,...,N)(1,2,\dots,N)(1,2,...,N):
- 选择一对满足 1≤i<j≤N1 \le i < j \le N1≤i<j≤N 的整数 (i,j)(i,j)(i,j),交换 PiP_iPi 和 PjP_jPj 的值。
记 KKK 为将 PPP 变为有序序列所需的最小操作次数。
请你求出:在所有长度为 KKK 的最优操作序列中,可以作为第一个操作的不同 (i,j)(i,j)(i,j) 对的数量 。
(注:两个操作不同当且仅当选择的数对 (i,j)(i,j)(i,j) 不同)
解题思路
首先我们想一下,如何才能找出,最短的操作方法。这里其实能想到一个非常显然的方式,就是我们从左到右遍历,每次找到一个不应该在这个位置上的元素,我们就交换,把正确的数字换过来,这样的操作对于最终答案一定是最优的。
具体证明的话大家可以去网上搜循环分解。
假设我们现在有一个长度为 333 的数列 [1,2,3][1, 2 ,3][1,2,3],然后我们进行下列交换:(1,2)(1,3)(1, 2) (1, 3)(1,2)(1,3),然后会变成 [3,1,2][3, 1, 2][3,1,2]。我们想一想,我们交换了第一个位置和第二个位置之后,又交换了第一个位置和第三个位置,那么是不是就说明其实第二个位置和第三个位置也有交换呢,因为第二个位置换到第一个位置之后又被第三个位置换走了啊。
所以我们这个时候就能得到正解了,先明确哪些位置之间存在交换,那么第一次操作就可以选择这些位置当中的任意两个位置作为第一次操作。
在代码实现上,我们先跑一遍贪心,看看那些位置之间存在位置交换,为了方便大家理解,我们用原题中的第三个样例举例:
15 5 13 17 9 11 20 4 14 16 6 3 8 19 12 7 10 18 2 1 (1, 20)
1 5 13 17 9 11 20 4 14 16 6 3 8 19 12 7 10 18 2 15 (2, 19)
1 2 13 17 9 11 20 4 14 16 6 3 8 19 12 7 10 18 5 15 (3, 12)
1 2 3 17 9 11 20 4 14 16 6 13 8 19 12 7 10 18 5 15 (4, 8)
1 2 3 4 9 11 20 17 14 16 6 13 8 19 12 7 10 18 5 15 (5, 19)
1 2 3 4 5 11 20 17 14 16 6 13 8 19 12 7 10 18 9 15 (6, 11)
1 2 3 4 5 6 20 17 14 16 11 13 8 19 12 7 10 18 9 15 (7, 16)
1 2 3 4 5 6 7 17 14 16 11 13 8 19 12 20 10 18 9 15 (8, 13)
1 2 3 4 5 6 7 8 14 16 11 13 17 19 12 20 10 18 9 15 (9, 19)
1 2 3 4 5 6 7 8 9 16 11 13 17 19 12 20 10 18 14 15 (10, 17)
1 2 3 4 5 6 7 8 9 10 11 13 17 19 12 20 16 18 14 15 (12, 15)
1 2 3 4 5 6 7 8 9 10 11 12 17 19 13 20 16 18 14 15 (13, 15)
1 2 3 4 5 6 7 8 9 10 11 12 13 19 17 20 16 18 14 15 (14, 19)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 17 20 16 18 19 15 (15, 20)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 20 16 18 19 17 (16, 17)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 20 18 19 17 (17, 20)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 这个就是我们数列的变化过程,后面括号是每一次交换哪两个位置,然后我们每次找到这两个位置之后,给二者进行建边,就有了下面这个图。
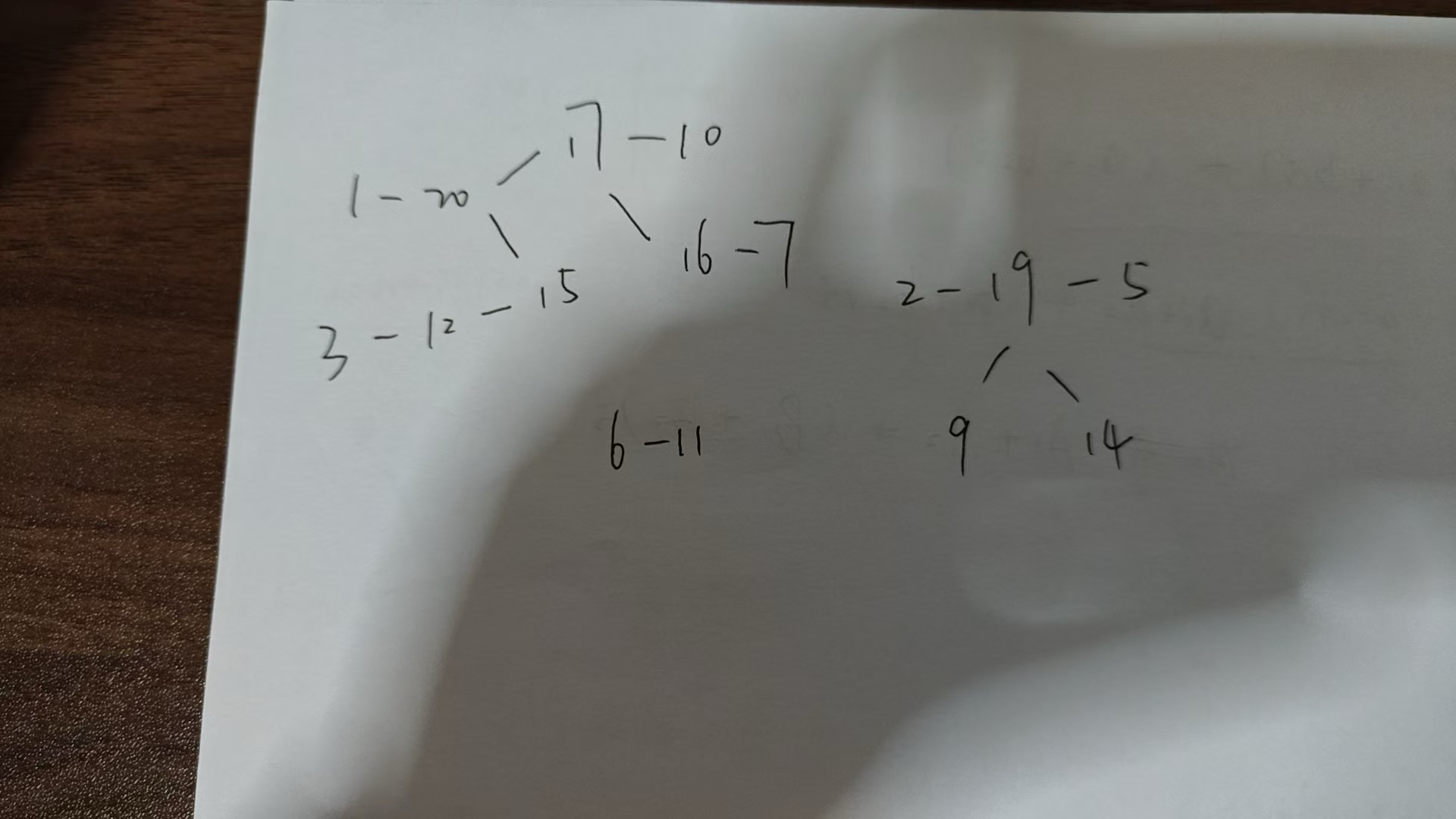
然后任意两个联通的位置都能作为这次最小交换的第一个位置,计算每一个联通块的大小,然后等差数列求和就行了。
这里我们用带权并查集实现即可。
代码
cpp
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn = 3e5 + 5;
int n, f[maxn], num[maxn], pos[maxn], p[maxn];
int solve(int x)
{
return (x - 1) * x / 2;
}
int find(int x)
{
if (f[x] == x)
return x;
return f[x] = find(f[x]);
}
void merge(int x, int y)
{
x = find(x), y = find(y);
f[x] = y;
num[y] += num[x];
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n;
for (int i = 1; i <= n; i++)
{
f[i] = i, num[i] = 1;
cin >> p[i];
pos[p[i]] = i;
}
for (int i = 1; i <= n; i++)
if (pos[i] != i)
{
int x = p[i];
swap(p[i], p[pos[i]]);
swap(pos[i], pos[x]);
merge(i, x);
}
int ans = 0;
for (int i = 1; i <= n; i++)
if (f[i] == i)
ans += solve(num[i]);
cout << ans;
return 0;
}F - Starry Landscape Photo
大致题意
在阿特寇德星球的夜空中,有 NNN 颗星星排成一条东西走向的直线。从东往西数的第 iii 颗星(1≤i≤N1 \le i \le N1≤i≤N),在这 NNN 颗星中的亮度排名为 BiB_iBi。
高桥按照以下步骤拍摄夜空照片,请计算他能拍出的不同星星集合的数量(空集不计入):
- 选择一对整数 (l,r)(l,r)(l,r)(满足 1≤l≤r≤N1 \le l \le r \le N1≤l≤r≤N),调整相机取景范围,使得从东往西数第 lll 到第 rrr 颗星恰好全部纳入取景框,且框内不含其他星星。
- 选择一个整数 bbb(满足 1≤b≤N1 \le b \le N1≤b≤N),按下快门拍照,最终照片中会捕捉到取景框内、亮度排名为第 111 到第 bbb 名的所有星星,其余星星不会被捕捉。
解题思路
当亮度阈值 b=Nb=Nb=N 时,所有星星都能被捕捉。此时只需统计所有可能的连续区间 (l,r)(l,r)(l,r),方案数为 1+2+⋯+N=N(N+1)21+2+\dots+N = \frac{N(N+1)}{2}1+2+⋯+N=2N(N+1)。
随着 bbb 减小,亮度排名大于 bbb 的星星会被排除。此时会产生新的星星集合的充要条件是:被排除的星星位于某个连续区间的内部(非左右边界)。
- 若被排除的星星在区间边界,去掉它后的区间对应的星星集合,在更大的 bbb 时已经统计过;
- 只有排除内部星星,才会分割出之前未出现过的新集合。
对每颗星星 xxx(亮度排名为 BxB_xBx),计算:
- 其左侧连续的、亮度排名 ≤Bx\le B_x≤Bx 的星星数量(记为 LLL);
- 其右侧连续的、亮度排名 ≤Bx\le B_x≤Bx 的星星数量(记为 RRR)。
该星星被排除时,新增的方案数为 L×RL \times RL×R,这里的星星个数我们可以使用树状数组来进行计算。
综上,bbb 最大时候的方案数加上所有星星对应的新增方案数,即为最终不同星星集合的总数。
代码
cpp
#include <bits/stdc++.h>
#define int long long
#define lowbit(i) i & (-i)
using namespace std;
const int maxn = 5e5 + 5;
int n, t[maxn];
void update(int pos)
{
for (int i = pos; i <= n; i += lowbit(i))
t[i] += 1;
}
int query(int pos)
{
int ans = 0;
for (int i = pos; i >= 1; i -= lowbit(i))
ans += t[i];
return ans;
}
signed main()
{
cin >> n;
int ans = 0;
for (int i = 1; i <= n; i++)
{
int b;
cin >> b;
int l = query(b - 1);
ans += l * (b - l - 1);
update(b);
}
ans += n * (n + 1) / 2;
cout << ans;
return 0;
}G - Linear Inequation
大致题意
给定一个长度为 NNN 的正整数序列 A=(A1,A2,...,AN)A = (A_1,A_2,\dots,A_N)A=(A1,A2,...,AN),以及一个正整数 MMM。
请你求出满足以下条件的、长度为 NNN 的非负整数序列 x=(x1,x2,...,xN)x = (x_1,x_2,\dots,x_N)x=(x1,x2,...,xN) 的数量:
∑i=1NAi⋅xi≤M\sum_{i=1}^{N} A_i \cdot x_i \le Mi=1∑NAi⋅xi≤M
由于答案可能很大,请输出答案对 998244353 取模的结果。
解题思路
我的评价是逆天出题人为了防 AK 整了个数论题,这题的话实际上就是一个 Bostan-Mori(应该没拼错吧)板子题,我也是现学了这个东西才把这道题 a 掉。看完这道题的题目,大部分朋友应该都能想出可以用背包来做这个题,但是因为这里的 mmm 太大了,所以我们就只能考虑用生成函数(大家如果不会理论的东西的话就没招了,自己去学吧)。
首先我们在 AAA 数列的最后面加一个元素 111,这样的话我们的问题就变成了 ∑i=1N+1Aixi=M\sum^{N + 1}_{i=1} {A_i x_i} = M∑i=1N+1Aixi=M,然后我们求每一个 AiA_iAi 的生成函数,那么第 iii 个元素的生成函数就是 1+1+1+ xAix^{A_i}xAi +x2Ai+...+ x^{2 A_i} + ...+x2Ai+... = 11−xAi\frac{1}{1-x^{A_i}}1−xAi1 = F(i)F(i)F(i)。
然后我们就要去求 ∏i=1N+1F(i)\prod_{i=1}^{N + 1} {F(i)}∏i=1N+1F(i) 中 xmx^mxm 的系数,然后就可以用 Bostan-Mori 处理了,这个算法就是可以把 求第 M 项 这个问题转化成 求第 M / 2 项,然后配合着多项式乘法等操作把问题规模减半。
不过除此之外要注意一些细节问题,比如此题需要取模,所以要使用 FFT 的一个进阶版本 NTT,然后要注意原根的值等等。
破数论真是一学一个不吱声啊......
代码
cpp
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
int N;
ll M;
ll dp[10101];
const ll mo = 998244353;
ll modpow(ll a, ll n = mo - 2)
{
ll r = 1;
a %= mo;
while (n)
r = r * ((n % 2) ? a : 1) % mo, a = a * a % mo, n >>= 1;
return r;
}
template <class T>
using vec = vector<T>;
template <class T>
vec<T> fft(vec<T> v, bool rev = false)
{
int n = v.size(), i, j, m;
for (int m = n; m >= 2; m /= 2)
{
T wn = modpow(5, (mo - 1) / m);
if (rev)
wn = modpow(wn);
for (i = 0; i < n; i += m)
{
T w = 1;
for (int j1 = i, j2 = i + m / 2; j2 < i + m; j1++, j2++)
{
T t1 = v[j1], t2 = v[j2];
v[j1] = (t1 + t2 + mo) % mo;
v[j2] = ll(t1 + mo - t2) * w % mo;
while (v[j1] >= mo)
v[j1] -= mo;
w = (ll)w * wn % mo;
}
}
}
for (i = 0, j = 1; j < n - 1; j++)
{
for (int k = n >> 1; k > (i ^= k); k >>= 1)
;
if (i > j)
swap(v[i], v[j]);
}
if (rev)
{
ll rv = modpow(n);
for (int i = 0; i < n; i++)
v[i] = (ll)v[i] * rv % mo;
}
return v;
}
template <class T>
vec<T> MultPoly(vec<T> P, vec<T> Q, bool resize = false, bool recover = false)
{
int len = 0;
if (resize)
{
int maxind = 0, pi = -1, qi = -1, i;
int s = 2;
len = P.size() + Q.size() - 1;
for (int i = 0; i < P.size(); i++)
if (abs(P[i]))
pi = i;
for (int i = 0; i < Q.size(); i++)
if (abs(Q[i]))
qi = i;
if (pi == -1 || qi == -1)
return {};
maxind = pi + qi + 1;
while (s * 2 < maxind)
s *= 2;
if (s <= 64)
{
vec<T> R(s * 2);
for (int x = 0; x <= pi; x++)
for (int y = 0; y <= qi; y++)
(R[x + y] += P[x] * Q[y]) %= mo;
if (recover)
R.resize(len);
return R;
}
vec<T> P2(s * 2), Q2(s * 2);
for (int i = 0; i < pi + 1; i++)
P2[i] = P[i];
for (int i = 0; i < qi + 1; i++)
Q2[i] = Q[i];
swap(P, P2), swap(Q, Q2);
}
P = fft(P), Q = fft(Q);
for (int i = 0; i < P.size(); i++)
P[i] = (ll)P[i] * Q[i] % mo;
P = fft(P, true);
if (resize && recover)
P.resize(len);
return P;
}
ll bostan(vector<ll> P, vector<ll> Q, ll N)
{
if (N == 0)
{
return P[0] % mo * modpow(Q[0] % mo) % mo;
}
int SQ = Q.size(), i;
vector<ll> MQ = Q;
for (int i = 0; i < MQ.size(); i++)
if (i % 2 == 1)
MQ[i] = (mo - MQ[i]) % mo;
vector<ll> P2 = MultPoly(P, MQ, 1);
vector<ll> Q2 = MultPoly(Q, MQ, 1);
P2.resize(2 * SQ + 1);
Q2.resize(2 * SQ + 1);
vector<ll> S, T;
for (int i = 0; i < SQ - 1; i++)
S.push_back(P2[i * 2 + (N % 2)] % mo);
for (int i = 0; i < SQ; i++)
T.push_back(Q2[i * 2] % mo);
return bostan(S, T, N / 2);
}
void solve()
{
int i, j, k, l, r, x, y;
string s;
cin >> N >> M;
queue<vec<ll>> Q;
Q.push({1, mo - 1});
for (int i = 0; i < N; i++)
{
cin >> x;
vec<ll> V(x + 1);
V[0] = 1;
V[x] = mo - 1;
Q.push(V);
}
while (Q.size() > 1)
{
auto a = Q.front();
Q.pop();
Q.push(MultPoly(a, Q.front(), 1));
Q.pop();
}
vector<ll> A = {1};
vector<ll> B = Q.front();
cout << bostan(A, B, M) << endl;
}
int main()
{
solve();
return 0;
}然后鄙人搞了一个 abc 的刷题群,每周四晚上免费讲解,有兴趣的朋友可以进群。

二维码有时间限制,想要进群的话也可以私聊。