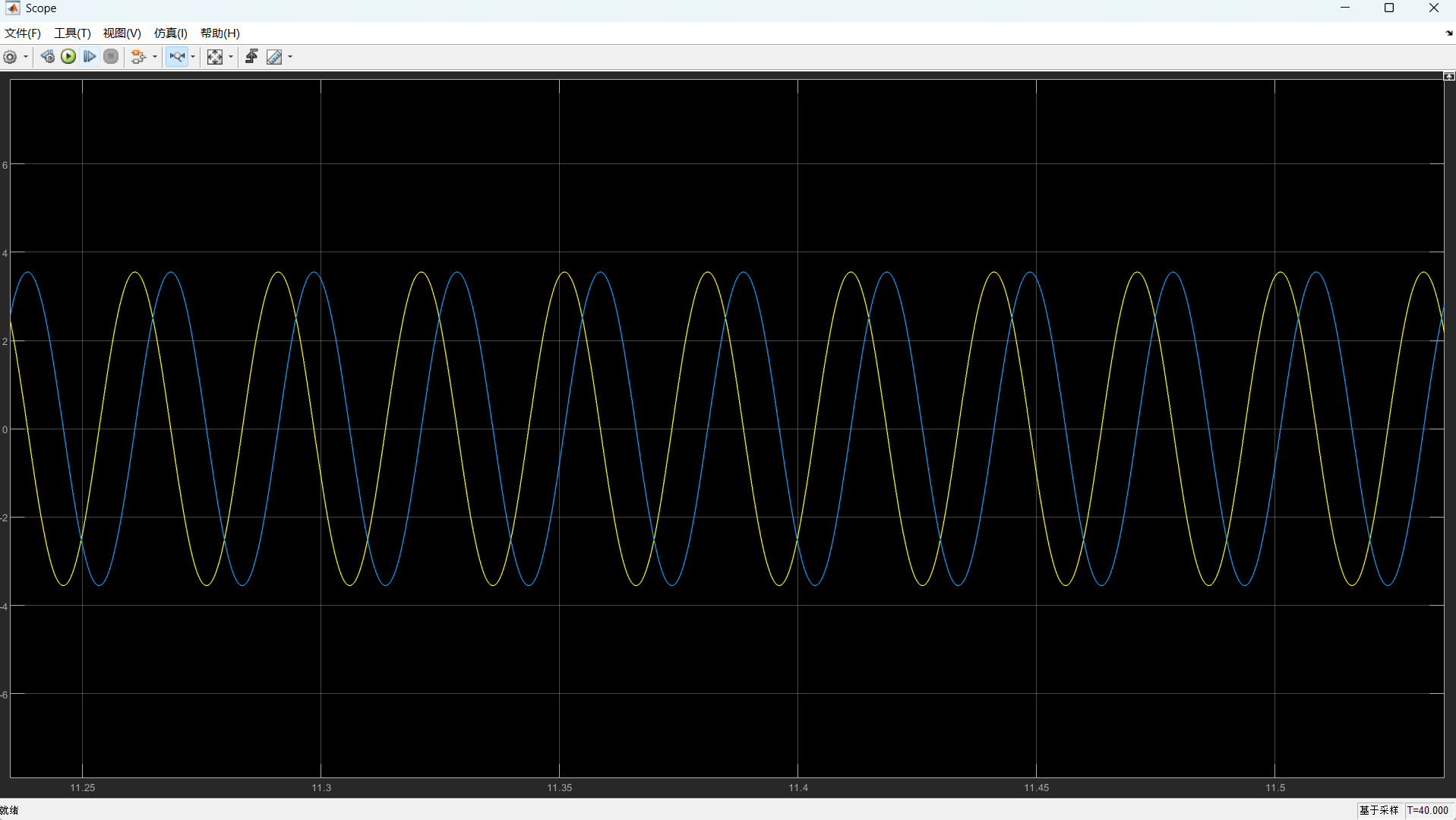
通过i_α和i_β估计反电势e_α和e_β
一、龙博格观测器简介
龙博格观测器,一种典型的全维状态观测器,依赖系统的输出状态与搭建的状态误差收敛状态对状态进行观测
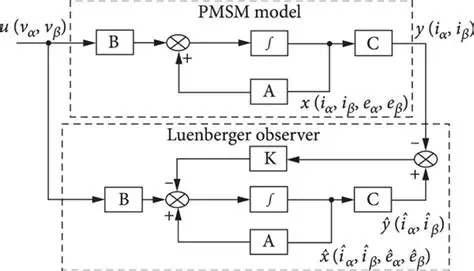
假设一个系统为:
{ x ˙ = A x + B u y = C x \left\{ \begin{aligned} \dot{x} &= A x + B u \\ y &= C x \end{aligned} \right. {x˙y=Ax+Bu=Cx
根据框图格式,构建观测器如下(K为增益):
{ x ^ ˙ = A x ^ + B u + K ( y − y ^ ) y ^ = C x ^ \left\{ \begin{aligned} \dot{\hat{x}} &= A \hat{x} + B u+K(y-\hat{y}) \\ \hat{y} &= C \hat{x} \end{aligned} \right. {x^˙y^=Ax^+Bu+K(y−y^)=Cx^
进一步,即状态x的观测值为:
x ^ ˙ = ( A − K C ) x ^ + B u + K y (式 1 ) \ \dot{\hat{x}}= (A-KC) \hat{x} + B u+Ky \ (式1) x^˙=(A−KC)x^+Bu+Ky (式1)
进一步,离散化后状态x为:
x ^ ( k + 1 ) = [ ( A − K C ) x ^ ( k ) + B u ( k ) + K y ( k ) ] ∗ T s + x ^ ( k ) \ {\hat{x}(k+1)}=[ (A-KC) \hat{x}(k) + B u(k)+Ky (k) ]*T_s+\hat{x}(k)\ x^(k+1)=[(A−KC)x^(k)+Bu(k)+Ky(k)]∗Ts+x^(k)
在PMSM控制中,我们通过对输出状态 i a \ i_a ia 和 i β \ i_β iβ 的追踪实现对反电动势 e a \ e_a ea 与 e a \ e_a ea 的观测,进而通过PLL可以提取PMSM的转子信息
二、状态变量推导
表贴式PMSM两相静止坐标系下电压方程:
{ u α = R s i α + L s d i α d t + e α u β = R s i β + L s d i β d t + e β \left\{ \begin{aligned} u_{\alpha} &= R_s i_{\alpha} + L_s \frac{di_{\alpha}}{dt} + e_{\alpha} \\ u_{\beta} &= R_s i_{\beta} + L_s \frac{di_{\beta}}{dt} + e_{\beta} \end{aligned} \right. ⎩ ⎨ ⎧uαuβ=Rsiα+Lsdtdiα+eα=Rsiβ+Lsdtdiβ+eβ
其中,反电动势为:
{ e α = − ω r ψ f sin ( θ r ) e β = ω r ψ f cos ( θ r ) \left\{ \begin{aligned} e_{\alpha} = -\omega_{r} \psi_{f} \sin \left( \theta_{r} \right) \\ e_{\beta} = \omega_{r} \psi_{f} \cos \left( \theta_{r} \right) \end{aligned} \right. {eα=−ωrψfsin(θr)eβ=ωrψfcos(θr)
其中, ω r \ \omega_{r} ωr为电角度、 θ r \ \theta_{r} θr为转子位置、 ψ f \ \psi_{f} ψf为永磁体磁链
由假设近似: ω r ˙ = 0 \ \dot{ \omega_{r} }=0 ωr˙=0 , d θ r d t = ω r \ \frac{d\theta_r}{dt} = \omega_r dtdθr=ωr从电压方程解出电流导数和反电势导数:
d i α d t = 1 L s ( u α − R s i α − e α ) \frac{di_{\alpha}}{dt} = \frac{1}{L_s}(u_{\alpha} - R_s i_{\alpha} - e_{\alpha}) dtdiα=Ls1(uα−Rsiα−eα)
d i β d t = 1 L s ( u β − R s i β − e β ) \frac{di_{\beta}}{dt} = \frac{1}{L_s}(u_{\beta} - R_s i_{\beta} - e_{\beta}) dtdiβ=Ls1(uβ−Rsiβ−eβ)
d e α d t = d d t ( − ω r ψ f sin ( θ r ) ) = − ω r d d t ( ψ f sin ( θ r ) ) ≈ − ω r e β \frac{de_{\alpha}}{dt} = \frac{d}{dt} \Bigl(-\omega_{r} \psi_{f} \sin(\theta_{r}) \Bigr) = -\omega_{r} \frac{d}{dt} \Bigl( \psi_{f} \sin(\theta_{r}) \Bigr) \approx -\omega_{r} e_{\beta} dtdeα=dtd(−ωrψfsin(θr))=−ωrdtd(ψfsin(θr))≈−ωreβ
d e β d t = d d t ( ω r ψ f cos ( θ r ) ) = ω r d d t ( ψ f cos ( θ r ) ) ≈ ω r e α \frac{de_{\beta}}{dt} = \frac{d}{dt} \Bigl( \omega_{r} \psi_{f} \cos(\theta_{r}) \Bigr) = \omega_{r} \frac{d}{dt} \Bigl( \psi_{f} \cos(\theta_{r}) \Bigr) \approx \omega_{r} e_{\alpha} dtdeβ=dtd(ωrψfcos(θr))=ωrdtd(ψfcos(θr))≈ωreα
故而状态空间方程 构建如下:
状态空间方程为: d d t [ i α i β e α e β ] = [ − R s L s 0 − 1 L s 0 0 − R s L s 0 − 1 L s 0 0 0 − ω r 0 0 ω r 0 ] [ i α i β e α e β ] + [ 1 L s 0 0 1 L s 0 0 0 0 ] [ u α u β 0 0 ] \frac{d}{d t}\left[\begin{array}{c} i_{\alpha} \\ i_{\beta} \\ e_{\alpha} \\ e_{\beta} \end{array}\right] = \left[\begin{array}{cccc} -\frac{R_{s}}{L_{s}} & 0 & -\frac{1}{L_{s}} & 0 \\ 0 & -\frac{R_{s}}{L_{s}} & 0 & -\frac{1}{L_{s}} \\ 0 & 0 & 0 & -\omega_{r} \\ 0 & 0 & \omega_{r} & 0 \end{array}\right] \left[\begin{array}{c} i_{\alpha} \\ i_{\beta} \\ e_{\alpha} \\ e_{\beta} \end{array}\right] + \left[\begin{array}{cc} \frac{1}{L_{s}} & 0 \\ 0 & \frac{1}{L_{s}} \\ 0 & 0 \\ 0 & 0 \end{array}\right] \left[\begin{array}{c} u_{\alpha} \\ u_{\beta} \\ 0 \\ 0 \end{array}\right] dtd iαiβeαeβ = −LsRs0000−LsRs00−Ls100ωr0−Ls1−ωr0 iαiβeαeβ + Ls10000Ls100 uαuβ00
输出方程为: [ i α i β ] = [ 1 0 0 0 0 1 0 0 ] [ i α i β e α e β ] \left[\begin{array}{l} i_{\alpha} \\ i_{\beta} \end{array}\right] = \left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{array}\right] \left[\begin{array}{l} i_{\alpha} \\ i_{\beta} \\ e_{\alpha} \\ e_{\beta} \end{array}\right] [iαiβ]=[10010000] iαiβeαeβ
三、实现过程
仿照一、中,对上面给出的状态方程设计Lunberger观测器如下:
d d t [ i ^ α i ^ β e ^ α e ^ β ] = A [ i ^ α i ^ β e ^ α e ^ β ] + B [ u α u β 0 0 ] + K ( [ i α i β 0 0 ] − [ i ^ α i ^ β 0 0 ] ) ( 式 2 ) \frac{d}{d t}\left[\begin{array}{c} \hat{i}{\alpha} \\ \hat{i}{\beta} \\ \hat{e}{\alpha} \\ \hat{e}{\beta} \end{array}\right] = \mathbf{A}\left[\begin{array}{c} \hat{i}{\alpha} \\ \hat{i}{\beta} \\ \hat{e}{\alpha} \\ \hat{e}{\beta} \end{array}\right] + \mathbf{B}\left[\begin{array}{c} u_{\alpha} \\ u_{\beta} \\ 0 \\ 0 \end{array}\right] + \mathbf{K}\left( \left[\begin{array}{c} i_{\alpha} \\ i_{\beta}\\0 \\0 \end{array}\right] - \left[\begin{array}{c} \hat{i}{\alpha} \\ \hat{i}{\beta} \\0 \\0 \end{array}\right] \right)(式2) dtd i^αi^βe^αe^β =A i^αi^βe^αe^β +B uαuβ00 +K iαiβ00 − i^αi^β00 (式2)
其中,系数矩阵A、B、C为:
A = [ − R s L s 0 − 1 L s 0 0 − R s L s 0 − 1 L s 0 0 0 − ω r 0 0 ω r 0 ] \mathbf{A}=\left[\begin{array}{cccc} -\frac{R_{s}}{L_{s}} & 0 & -\frac{1}{L_{s}} & 0 \\ 0 & -\frac{R_{s}}{L_{s}} & 0 & -\frac{1}{L_{s}} \\ 0 & 0 & 0 & -\omega_{r} \\ 0 & 0 & \omega_{r} & 0 \end{array}\right] A= −LsRs0000−LsRs00−Ls100ωr0−Ls1−ωr0
B = [ 1 L s 0 0 1 L s 0 0 0 0 ] , C = [ 1 0 0 0 0 1 0 0 ] \mathbf{B}=\left[\begin{array}{cc} \frac{1}{L_{s}} & 0 \\ 0 & \frac{1}{L_{s}} \\ 0 & 0 \\ 0 & 0 \end{array}\right],\quad \mathbf{C}=\left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{array}\right] B= Ls10000Ls100 ,C=[10010000]
增益矩阵为:
K = [ K 1 0 0 0 0 K 1 0 0 K 2 0 0 0 0 K 2 0 0 ] \mathbf{K} = \left[ \begin{array}{cc} K_1 & 0 & 0& 0\\ 0 & K_1 & 0& 0\\ K_2 & 0 & 0& 0\\ 0 & K_2& 0& 0\\ \end{array} \right] K= K10K200K10K200000000
其中,K1是对电流的观测增益,K2是对反电动势的观测增益
状态变量,输入矩阵,输出矩阵分别为:
x = [ i α i β e α e α ] , u = [ u α u β 0 0 ] , y = [ i α i β 0 0 ] \mathbf{x}=\left[\begin{array}{c} i_{\alpha} \\ i_{\beta} \\ e_{\alpha} \\ e_{\alpha} \end{array}\right] ,\mathbf{u}=\left[\begin{array}{c} u_{\alpha} \\ u_{\beta} \\ 0 \\ 0 \end{array}\right] ,\mathbf{y}=\left[\begin{array}{c} i_{\alpha} \\ i_{\beta} \\ 0 \\ 0 \end{array}\right] x= iαiβeαeα ,u= uαuβ00 ,y= iαiβ00
对(式2)离散化后,得到反电动势的龙博格观测器为:
i ^ α ( k + 1 ) = i ^ α ( k ) + T [ − R s L s i ^ α ( k ) − 1 L s e ^ α ( k ) + 1 L s u α ( k ) + K 1 ( i α ( k ) − i ^ α ( k ) ) ] i ^ β ( k + 1 ) = i ^ β ( k ) + T [ − R s L s i ^ β ( k ) − 1 L s e ^ β ( k ) + 1 L s u β ( k ) + K 1 ( i β ( k ) − i ^ β ( k ) ) ] e ^ α ( k + 1 ) = e ^ α ( k ) + T [ − ω ^ e e ^ β ( k ) + K 2 ( i α ( k ) − i ^ α ( k ) ) ] e ^ β ( k + 1 ) = e ^ β ( k ) + T [ ω ^ e e ^ α ( k ) + K 2 ( i β ( k ) − i ^ β ( k ) ) ] \begin{aligned} \hat{i}{\alpha}(k+1) &= \hat{i}{\alpha}(k) + T\bigg[-\frac{R_s}{L_s}\hat{i}{\alpha}(k) - \frac{1}{L_s}\hat{e}{\alpha}(k) + \frac{1}{L_s}u_{\alpha}(k) + K_1\big(i_{\alpha}(k) - \hat{i}{\alpha}(k)\big)\bigg] \\ \hat{i}{\beta}(k+1) &= \hat{i}{\beta}(k) + T\bigg[-\frac{R_s}{L_s}\hat{i}{\beta}(k) - \frac{1}{L_s}\hat{e}{\beta}(k) + \frac{1}{L_s}u{\beta}(k) + K_1\big(i_{\beta}(k) - \hat{i}{\beta}(k)\big)\bigg] \\ \hat{e}{\alpha}(k+1) &= \hat{e}{\alpha}(k) + T\bigg[-\hat{\omega}e \hat{e}{\beta}(k) + K_2\big(i{\alpha}(k) - \hat{i}{\alpha}(k)\big)\bigg] \\ \hat{e}{\beta}(k+1) &= \hat{e}{\beta}(k) + T\bigg[\,\hat{\omega}e \hat{e}{\alpha}(k) + K_2\big(i{\beta}(k) - \hat{i}_{\beta}(k)\big)\bigg] \end{aligned} i^α(k+1)i^β(k+1)e^α(k+1)e^β(k+1)=i^α(k)+T[−LsRsi^α(k)−Ls1e^α(k)+Ls1uα(k)+K1(iα(k)−i^α(k))]=i^β(k)+T[−LsRsi^β(k)−Ls1e^β(k)+Ls1uβ(k)+K1(iβ(k)−i^β(k))]=e^α(k)+T[−ω^ee^β(k)+K2(iα(k)−i^α(k))]=e^β(k)+T[ω^ee^α(k)+K2(iβ(k)−i^β(k))]
T为采样时间
四、仿真
simulink搭建仿真验证如下:
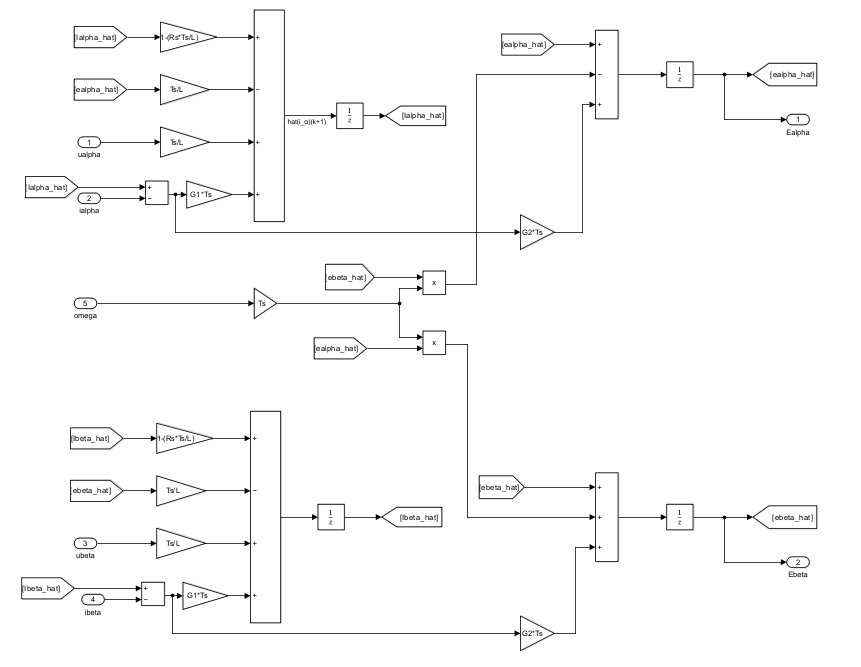
选取合适增益后运行,用示波器查看i_α和hat(i_α)波形发现观测收敛,如下:
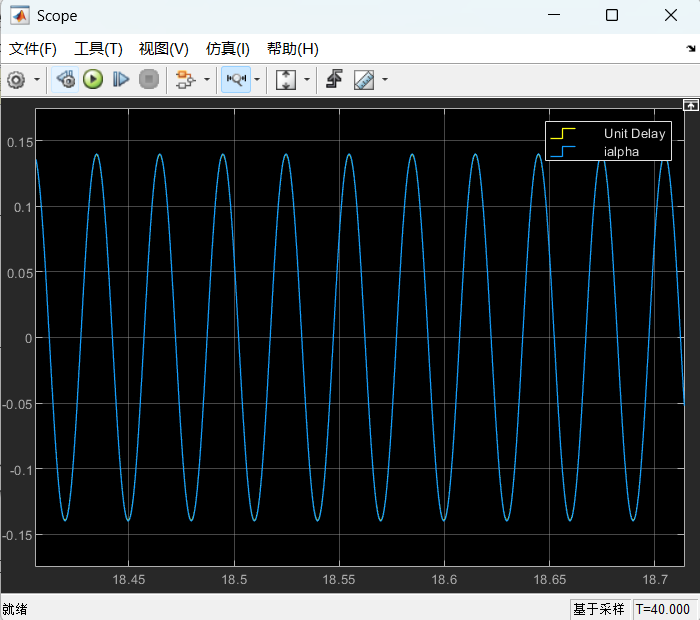
反电动势为: