【例3-3】医院设置（信息学奥赛一本通- P1338）

【题目描述】

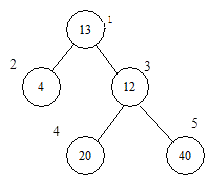
设有一棵二叉树（如下图），其中圈中的数字表示结点中居民的人口，圈边上数字表示结点编号。现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻结点之间的距离为1。就本图而言，若医院建在1处，则距离和=4+12+2×20+2×40=136；若医院建在3处，则距离和=4×2+13+20+40=81......

【输入】

第一行一个整数n，表示树的结点数（n≤100）。接下来的n行每行描述了一个结点的状况，包含三个整数，整数之间用空格（一个或多个）分隔，其中：第一个数为居民人口数；第二个数为左链接，为0表示无链接；第三个数为右链接，为0表示无链接。

【输出】

一个整数，表示最小距离和。

【输入样例】

复制代码

【输出样例】

复制代码

cpp 复制代码

//这道题可以当图来做，也可以当树来做，因为在树的分类里，我们就用树的指针来做
//因为题目说了，结点树小于等于100，我们就可以用顺序存储也可以用链式存储
//这里左右儿子都给出了，所以我们直接链式存储 
#include <bits/stdc++.h>
using namespace std;

struct node{
    int l;//左链接
    int r;//右链接
    int parents;//父节点
    int data;//该节点居民人口数
}tre[110];

int dis;
int a[110][110];//a[i][j]记录i点到j点距离
int mi=0x3f3f3f3f;//最小距离和
int root;//建医院的节点
int vis[110];//标记该结点距离是否被计算过

void dfs(int k,int cnt){//当前处于k结点 现在的距离系数（离root结点距离）
    if(tre[k].l && tre[k].l!=root && vis[tre[k].l]==0){//如果k结点有左儿子且左儿子不是这一次建医院的地方 且没有被计算过
        dis+=cnt*tre[tre[k].l].data;//距离增加系数*人口树
        vis[tre[k].l]=1;//标记计算过
        dfs(tre[k].l,cnt+1);//继续下次遍历
    }
    if(tre[k].r && tre[k].r!=root && vis[tre[k].r]==0){//如果k结点有右儿子且右儿子不是这一次建医院的地方 且没有被计算过
        dis+=cnt*tre[tre[k].r].data;
        vis[tre[k].r]=1;
        dfs(tre[k].r,cnt+1);
    }
    if(tre[k].parents && tre[k].parents!=root && vis[tre[k].parents]==0){//如果k结点有父节点且父节点不是这一次建医院的地方 且没有被计算过
        dis+=cnt*tre[tre[k].parents].data;
        vis[tre[k].parents]=1;
        dfs(tre[k].parents,cnt+1);
    }
}
int main(){
    int n;//结点数
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>tre[i].data>>tre[i].l>>tre[i].r;
        //左儿子节点存在，则左儿子的父节点就是i
        if(tre[i].l!=0) tre[tre[i].l].parents=i;
        //右儿子节点存在，则右儿子的父节点就是i
        if(tre[i].r!=0) tre[tre[i].r].parents=i;
    }
    root=1;
    while(root<n+1){//遍历n个节点分别建医院的距离和
        memset(vis,0,sizeof(vis));//每轮遍历要初始化vis数组
        dis=0;//本轮选择节点建医院的距离和
        vis[root]=1;
        dfs(root,1);//从第一个点开始 现在的距离系数
        root++;//每一轮root+1,代表一个新的地方建医院
        mi=min(dis,mi);
    }
    cout<<mi;
}