DAY 37 MLP 神经网络的训练

我们需要知道以下关于MLP的概念

1. 梯度下降的思想

2. 激活函数的作用

3. 损失函数的作用

4. 优化器

5. 神经网络的概念

神经网络由于内部比较灵活，所以封装的比较浅，可以对模型做非常多的改进，而不像机器学习三行代码固定。

零基础吃透 MLP 与神经网络核心概念（通俗版）

先先快速回顾MLP（多层感知机）的核心定义：MLP 是最基础的全连接神经网络 ，由输入层、隐藏层、输出层组成，每层的神经元都和下一层的所有神经元相连（全连接），是学习深度学习的入门基石。

接下来我会用生活化的类比 + 代码实例 + 核心逻辑，把你问的 5 个核心概念拆解得明明白白，全程避开复杂公式，只讲本质。

---

一、梯度下降的思想：模型的 "下山找路" 法则

1. 通俗类比：盲人下山找山谷

想象你是一个盲人，站在一座山上（这座山的高度代表损失函数的值，山谷就是损失最小的地方），你的目标是走到山谷最低点。你该怎么做？

• 第一步：感受脚下的地面往哪个方向倾斜最陡 （这就是梯度，梯度的方向是损失函数上升最快的方向）；
• 第二步：往倾斜最陡的反方向 走一小步（这就是负梯度方向）；
• 第三步：重复前两步，直到走到山谷（损失不再下降）。

这就是梯度下降 的核心思想 ------沿着损失函数的负梯度方向，一步步调整模型的参数，让损失函数的值越来越小。

2. 核心定义

• 梯度：是损失函数对模型每个参数的偏导数组成的向量，它告诉我们 "参数往哪个方向变，损失会上升得最快"。
• 梯度下降 ：反其道而行之，让参数沿着负梯度方向更新，从而让损失不断减小。

3. 结合代码的实际体现

在我们之前的 MLP 训练代码中，梯度下降的过程被这三行代码实现：

# 1. 计算损失（知道自己当前在"山的哪个高度"）
loss = criterion(y_pred, y_train_tensor)
# 2. 反向传播：计算梯度（感受"地面的倾斜方向"）
loss.backward()
# 3. 更新参数：往负梯度方向走一步（由优化器执行）
optimizer.step()

4. 关键补充：学习率的作用

"走一小步" 的 "步长" 就是学习率（lr）：

• 步长太大：可能一步跨出山谷，直接到对面的山坡（损失反而上升，模型不收敛）；
• 步长太小：走到山谷要花很多步（训练速度慢）；
• 我们代码中用的lr=0.01就是一个适中的步长。

---

二、激活函数的作用：给神经网络 "注入非线性"

1. 通俗类比：从 "一根筋" 到 "灵活思考"

如果没有激活函数，MLP 的每一层都是线性变换 （比如y = w*x + b），哪怕叠 100 层，最终的结果还是一个线性变换（相当于 y = a*x + b），只能拟合简单的直线关系，就像一个 "一根筋" 的人，只会用直线看世界。

而激活函数 就是给模型加入非线性，让模型能 "弯曲" 起来，拟合复杂的曲线关系（比如房价和面积的非线性关系、图片中物体的边缘特征）。

2. 核心定义

激活函数是非线性函数，作用是对神经元的输出进行 "非线性变换"，让神经网络能够学习复杂的非线性规律。

3. 举个直观的例子

比如我们要拟合这个曲线：y = x² + 0.5（非线性）。

• 没有激活函数的 MLP：无论叠多少层，都只能拟合出一条直线，永远无法贴近这个曲线；
• 有 ReLU 激活函数的 MLP：就能通过非线性变换，拟合出这条曲线的形状。

4. 常见激活函数及代码体现

激活函数	特点	代码中的使用
ReLU（最常用）	计算快、缓解梯度消失，适合隐藏层	self.relu = nn.ReLU()
Sigmoid	输出 0~1，适合二分类的输出层	nn.Sigmoid()
Softmax	输出各分类的概率（和为 1），适合多分类的输出层	nn.Softmax(dim=1)

我们之前的 MLP 代码中，隐藏层用了 ReLU：

def forward(self, x):
    out = self.fc1(x)  # 线性变换
    out = self.relu(out)  # 非线性变换（核心！）
    out = self.fc2(out)
    return out

5. 关键结论

没有激活函数的神经网络 = 线性回归 ，激活函数是神经网络能学习复杂规律的核心前提。

---

三、损失函数的作用：模型的 "成绩单"

1. 通俗类比：老师给学生判作业

模型的预测结果就像学生的作业答案，损失函数就是老师，负责对比 "标准答案（真实标签）" 和 "作业答案（模型预测）"，算出学生错了多少。

损失函数的值越大，说明模型预测得越差；值越小，说明模型预测得越准。

2. 核心定义

损失函数（Loss Function）是衡量模型预测值与真实值之间误差的函数，是模型优化的 "目标"（我们的目标是让损失函数的值最小）。

3. 不同任务的损失函数（结合代码）

损失函数的选择和任务类型强相关，主要分两类：

（1）回归任务（预测连续数值，比如房价、温度）

• 常用损失：均方误差（MSE） 计算方式：(预测值-真实值)²的平均值代码：criterion = nn.MSELoss()

  例子：真实房价 100 万，模型预测 90 万，MSE 损失就是(90-100)²/1 = 100。

（2）分类任务（预测离散类别，比如手写数字识别、猫狗分类）

• 常用损失：交叉熵损失（CrossEntropyLoss） 计算方式：衡量模型预测的概率分布和真实标签的分布差异代码：criterion = nn.CrossEntropyLoss()

  例子：真实标签是 "数字 5"，模型预测 "5" 的概率是 0.1，预测 "3" 的概率是 0.8，交叉熵损失就会很大。

4. 代码中的作用

损失函数是连接预测和真实值的桥梁，没有它，模型就不知道自己 "错在哪"，也就无法通过梯度下降优化。

---

四、优化器：模型的 "学习助手"

1. 通俗类比：给盲人下山配 "导航仪"

梯度下降告诉我们 "要往负梯度方向走"，但具体怎么走路、走多快、要不要调整步长，就是优化器的工作。

你可以把优化器理解为模型的 "学习助手"，它负责根据梯度计算的结果，自动调整模型的参数，让损失更快地减小。

2. 核心定义

优化器是执行梯度下降算法的工具，它封装了参数更新的逻辑，解决了 "如何高效调整参数" 的问题。

3. 常见优化器及特点

优化器	特点	代码中的使用
SGD（随机梯度下降）	基础优化器，简单但收敛慢	torch.optim.SGD(model.parameters(), lr=0.01)
Adam（最常用）	结合了动量和自适应学习率，收敛快、稳定	torch.optim.Adam(model.parameters(), lr=0.01)
RMSprop	适合处理非平稳数据，常用于 RNN	torch.optim.RMSprop(model.parameters(), lr=0.01)

4. 代码中的核心作用

我们之前的代码中，优化器的核心工作有两个：

# 1. 清空上一轮的梯度（避免梯度累积）
optimizer.zero_grad()
# 2. 根据梯度更新参数（执行梯度下降）
optimizer.step()

5. 关键补充：优化器和梯度下降的关系

• 梯度下降 是思想（往负梯度方向走）；
• 优化器 是实现这个思想的工具（不同的优化器有不同的走路方式）。

---

五、神经网络的概念：模仿人脑的 "数学拼图"

1. 通俗类比：人脑的神经元网络

人脑中有上千亿个神经元，每个神经元接收其他神经元的信号，处理后再传递给下一个神经元。

神经网络就是模仿人脑神经元连接方式的数学模型，它由一个个 "人工神经元" 组成，通过调整神经元之间的连接强度（参数），学习数据中的规律。

2. 核心定义

神经网络是由多层人工神经元组成的模型 ，通过线性变换 + 非线性激活的组合，学习数据的特征和规律，最终实现预测、分类等任务。

3. 神经网络的基本结构（以 MLP 为例）

• 输入层：接收原始数据（比如我们的 MLP 中，输入层有 2 个神经元，对应 2 个特征）；
• 隐藏层：提取数据的特征（比如我们的 MLP 中，隐藏层有 10 个神经元，负责学习特征之间的关系）；
• 输出层：输出预测结果（比如我们的 MLP 中，输出层有 1 个神经元，对应回归任务的预测值）。

4. 神经网络的核心特点（回应你最后一句话）

你说 "神经网络封装得浅，灵活度高，不像机器学习三行代码固定"，这是非常关键的点：

传统机器学习算法 （比如线性回归、决策树、SVM）：框架已经固定，通常调用库的 API 只需几行代码（比如model = LinearRegression()，model.fit(X,y)），能调整的参数很少；

神经网络（比如 MLP、CNN、RNN）：

• 可以自己定义层的数量（比如隐藏层从 1 层加到 3 层）；
• 可以自己定义每层的神经元数量（比如隐藏层从 10 个加到 100 个）；
• 可以自己选择激活函数、损失函数、优化器；
• 可以自己设计网络的连接方式（比如全连接、卷积、循环）。

这种 "高灵活性" 正是神经网络能解决复杂任务（比如图像识别、大语言模型）的原因。

5. 代码中的神经网络体现

我们的 MLP 就是一个最简单的神经网络：

class MLP(nn.Module):
    def __init__(self):
        super(MLP, self).__init__()
        self.fc1 = nn.Linear(2, 10)  # 输入层→隐藏层（2→10）
        self.fc2 = nn.Linear(10, 1)  # 隐藏层→输出层（10→1）
        self.relu = nn.ReLU()  # 非线性激活
    
    def forward(self, x):
        out = self.fc1(x)
        out = self.relu(out)
        out = self.fc2(out)
        return out

你可以轻松修改它：比如加一个隐藏层self.fc3 = nn.Linear(10, 5)，或者把神经元数量改成 20，这就是神经网络的灵活性。

---

总结：5 个概念的逻辑串联

这 5 个概念构成了神经网络训练的完整逻辑链：

1. 神经网络是我们的 "模型主体"，负责接收数据并输出预测；
2. 损失函数是 "裁判"，衡量模型预测的误差；
3. 梯度下降是 "优化思想"，告诉我们要往哪个方向调整参数；
4. 优化器是 "执行工具"，负责具体调整参数；
5. 激活函数是 "灵魂"，让神经网络能学习复杂的非线性规律。

而 MLP 作为最基础的神经网络，正是这 5 个概念的完美载体 ------ 通过它，你可以直观地看到每个概念在实际代码中的作用。

神经网络的训练过程（零基础友好版：从类比到代码拆解）

神经网络的训练过程可以类比成"学生刷题备考"的全过程，核心是 "输入数据→模型预测→判断错误→调整自身→重复优化"的循环。我会以 MLP（多层感知机）为例，把训练过程拆成 「训练前准备」「核心训练循环」「训练后验证」三个阶段，每个阶段都用生活化类比 + 代码实例 + 逐步解释 ，让你彻底看明白。

先给出整体逻辑框架：

训练前准备 → 多轮训练循环（Epoch） → 训练后验证
（备题+备学生） （每轮：做题→打分→改错题） （模拟考试+看效果）

一、先搞懂核心术语：训练的 "基本词汇"

在开始前，先明确两个关键名词，避免后续混淆：

• Epoch（训练轮数） ：把整个训练集完整过一遍，就是 1 个 Epoch。比如训练集有 700 个样本，把这 700 个样本都输入模型一次，就是 1 个 Epoch。通常会训练几十、上百个 Epoch，让模型学透规律。
• Batch（批次） ：如果训练集样本太多（比如 100 万），一次性输入模型会占满内存，所以把训练集分成若干个 "批次"，每次输入一个 Batch 训练（这叫小批量梯度下降）。零基础可以先忽略 Batch，用全量数据训练，更容易理解。

---

二、训练过程拆解：以 MLP 回归任务为例

我们延续之前的 "预测 y=2x1+3x2+0.5" 的例子，把训练过程一步步拆解开。

阶段 1：训练前的准备（备题 + 备学生）

就像学生备考前要准备练习题（数据） 、学生（模型） 、老师（损失函数 + 优化器），训练前也需要完成这三件事：

1. 准备并预处理数据（备题）

对应 "学生的练习题和考试卷"，包括数据生成 / 加载、归一化、转张量、划分训练集 / 测试集（训练集是练习题，测试集是考试卷）。

代码示例（回顾）：

import torch
import torch.nn as nn
import numpy as np
from sklearn.model_selection import train_test_split

# 1. 生成数据
np.random.seed(0)
n_samples = 1000
x = np.random.rand(n_samples, 2) * 10  # 特征（练习题题干）
y = 2 * x[:, 0] + 3 * x[:, 1] + 0.5 + np.random.randn(n_samples) * 0.1  # 标签（练习题答案）

# 2. 划分训练集（70%）和测试集（30%）
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=0)

# 3. 归一化（让数据更适合模型学习）
x_train_min = x_train.min(axis=0)
x_train_max = x_train.max(axis=0)
x_train_norm = (x_train - x_train_min) / (x_train_max - x_train_min)
x_test_norm = (x_test - x_train_min) / (x_train_max - x_train_min)

# 4. 转成PyTorch张量（模型能处理的格式）
x_train_tensor = torch.tensor(x_train_norm, dtype=torch.float32)
x_test_tensor = torch.tensor(x_test_norm, dtype=torch.float32)
y_train_tensor = torch.tensor(y_train, dtype=torch.float32).unsqueeze(1)
y_test_tensor = torch.tensor(y_test, dtype=torch.float32).unsqueeze(1)

2. 定义神经网络模型（备学生）

对应 "准备一个学生"，这个学生的 "大脑结构" 就是神经网络的层结构（输入层、隐藏层、输出层）。

代码示例（回顾）：

class MLP(nn.Module):
    def __init__(self):
        super(MLP, self).__init__()
        # 定义层：输入层（2维）→隐藏层（10维）→输出层（1维）
        self.fc1 = nn.Linear(2, 10)
        self.fc2 = nn.Linear(10, 1)
        self.relu = nn.ReLU()  # 激活函数（让学生有"灵活思考"的能力）
    
    # 定义前向传播：学生"思考问题"的路径
    def forward(self, x):
        out = self.fc1(x)
        out = self.relu(out)
        out = self.fc2(out)
        return out

# 实例化模型（创建一个"学生"）
model = MLP()

3. 定义损失函数和优化器（备老师）

• 损失函数：对应 "批改作业的老师"，负责给模型的预测打分（判断错了多少）。
• 优化器：对应 "讲题的老师"，负责告诉模型怎么调整自己的 "知识结构"（参数）来减少错误。

代码示例（回顾）：

# 损失函数：回归任务用均方误差（MSE）------衡量预测和真实值的误差
criterion = nn.MSELoss()

# 优化器：用Adam（最常用的"讲题老师"），学习率lr=0.01（老师告诉学生"改错题的步长"）
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

阶段 2：核心训练循环（学生刷题：每轮都做 "做题→打分→改错题"）

这是训练的核心，我们会重复多个 Epoch（轮数），每一轮都让模型完成 "前向传播→计算损失→反向传播→参数更新" 四个步骤，就像学生每一轮都做一套练习题，然后老师批改、讲解，学生改正错误。

核心逻辑：每个 Epoch 的 4 个步骤（对应代码逐行解释）

# 训练参数：训练100轮（学生做100套练习题）
epochs = 100
train_loss_list = []  # 保存每轮的损失，用于后续可视化
test_loss_list = []   # 保存每轮的测试损失

for epoch in range(epochs):
    # ---------------------- 步骤1：训练模式（学生进入刷题状态） ----------------------
    model.train()  # 启用训练相关的层（比如Dropout，本例用不到，但这是好习惯）
    
    # ---------------------- 步骤2：前向传播（学生做练习题） ----------------------
    y_pred_train = model(x_train_tensor)  # 把训练数据输入模型，得到预测值（学生写答案）
    
    # ---------------------- 步骤3：计算损失（老师批改作业，打分数） ----------------------
    train_loss = criterion(y_pred_train, y_train_tensor)  # 对比预测值和真实值，算出误差（分数）
    
    # ---------------------- 步骤4：清空梯度（避免上一轮的错误影响本轮） ----------------------
    optimizer.zero_grad()  # 梯度会累积，必须先清空，否则相当于学生把上一轮的错题和本轮混在一起改
    
    # ---------------------- 步骤5：反向传播（学生分析错题原因） ----------------------
    train_loss.backward()  # 计算损失对模型每个参数的梯度（学生找到"哪里错了、错多少"）
    
    # ---------------------- 步骤6：参数更新（学生改正错误，记住正确方法） ----------------------
    optimizer.step()  # 优化器根据梯度调整模型参数（学生按照老师的讲解，调整自己的知识结构）
    
    # ---------------------- 可选：测试集验证（学生做一次模拟考试） ----------------------
    model.eval()  # 评估模式（禁用训练相关的层，保证测试结果准确）
    with torch.no_grad():  # 禁用梯度计算，加快速度、节省内存
        y_pred_test = model(x_test_tensor)
        test_loss = criterion(y_pred_test, y_test_tensor)
    
    # ---------------------- 保存损失值（记录学生的学习进度） ----------------------
    train_loss_list.append(train_loss.item())
    test_loss_list.append(test_loss.item())
    
    # ---------------------- 打印进度（看学生的学习情况） ----------------------
    if (epoch + 1) % 10 == 0:
        print(f'Epoch [{epoch+1}/{epochs}], 训练损失：{train_loss.item():.4f}, 测试损失：{test_loss.item():.4f}')

每个步骤的通俗解读（关键！）

步骤	类比（学生刷题）	技术本质
前向传播	学生拿到练习题，根据自己的知识写出答案	数据通过模型的层结构，得到预测值
计算损失	老师对比标准答案和学生答案，算出错误分数	用损失函数计算预测值与真实值的误差
清空梯度	学生把上一轮的错题本清空，只改本轮的错	清空优化器中累积的梯度，避免跨轮干扰
反向传播	学生分析每道题错的原因（比如公式记错了、计算错了）	计算损失对模型所有参数的梯度（参数的调整方向和幅度）
参数更新	学生根据错误原因，记住正确的公式和计算方法	优化器沿负梯度方向调整模型参数，减小损失

阶段 3：训练后验证与可视化（看学生的最终成绩）

训练完成后，我们需要通过测试集验证 和损失曲线可视化，判断模型的学习效果（学生是否真的学会了，而不是死记硬背）。

1. 可视化损失曲线（看学生的学习趋势）

通过曲线能直观看到模型的损失是否下降、是否过拟合。

代码示例：

import matplotlib.pyplot as plt

# 解决中文显示问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 绘制训练和测试损失曲线
plt.figure(figsize=(10, 6))
plt.plot(train_loss_list, label='训练损失', color='blue', linewidth=2)
plt.plot(test_loss_list, label='测试损失', color='red', linewidth=2, linestyle='--')
plt.xlabel('训练轮数（Epoch）', fontsize=12)
plt.ylabel('损失值（Loss）', fontsize=12)
plt.title('MLP训练损失变化曲线', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True, alpha=0.3)
plt.show()

2. 用新数据测试模型（看学生的实际应用能力）

找一个新的样本输入模型，看预测结果是否接近真实值，验证模型的泛化能力。

代码示例：

# 测试数据：x1=0.5，x2=0.5（真实值=2*0.5+3*0.5+0.5=3）
test_x = torch.tensor([[0.5, 0.5]], dtype=torch.float32)
# 归一化（用训练集的统计量）
test_x_norm = (test_x - x_train_min) / (x_train_max - x_train_min)

# 模型预测
model.eval()
with torch.no_grad():
    test_y = model(test_x_norm)

print(f'测试输入[0.5, 0.5]的预测值：{test_y.item():.4f}')
print(f'真实值：3.0')

预期输出：预测值接近 3.0（比如 2.9876），说明模型学透了规律。

---

三、训练过程的核心规律与常见问题

1. 理想的训练趋势

• 训练损失和测试损失都逐渐下降，最终趋于平稳（学生越学越好，模拟考试分数也越来越高）。
• 测试损失略高于训练损失（正常现象，因为测试集是陌生题）。

2. 常见问题及解决办法

问题	现象	解决办法
过拟合（学生死记硬背）	训练损失持续下降，测试损失先降后升	增加训练数据、用 Dropout 层、L2 正则化、减少模型复杂度
欠拟合（学生没学会）	训练损失和测试损失都很高，且不下降	增加模型层数 / 神经元数、延长训练轮数、调整学习率
训练不收敛（学生学不会）	损失值波动很大或持续上升	减小学习率、检查数据预处理、更换优化器

3. 神经网络训练的灵活性（回应你之前的话）

和传统机器学习（比如线性回归）的 "固定代码模板" 不同，神经网络的训练过程可以灵活调整：

• 可以改模型结构（比如加隐藏层、改神经元数量）；
• 可以换损失函数（比如分类任务用交叉熵损失）；
• 可以换优化器（比如用 SGD 代替 Adam）；
• 可以调整训练参数（比如学习率、训练轮数）。

这种灵活性正是神经网络能解决复杂任务的关键。

---

四、总结：神经网络训练的 "一句话逻辑"

神经网络的训练过程，就是让模型在训练集上反复 "试错"，通过梯度下降不断调整自身参数，最终让预测值无限接近真实值的过程。

用更简洁的流程概括：

数据预处理 → 模型定义 → 损失函数/优化器选择 → 多轮训练循环（前向传播→计算损失→反向传播→参数更新） → 验证与可视化

你可以把整个训练过程的代码复制到 Python 文件中运行，逐行执行并观察输出，就能直观感受到模型的 "学习过程"。

零基础学 MLP 神经网络训练：从环境搭建到实战

作为你的老师，我会用最通俗的语言、最细致的步骤 拆解知识点，全程配合可运行的代码和直观的例子，确保你能一步步理解。首先明确学习的核心逻辑：先搭好环境（装 PyTorch/CUDA）→ 检查环境是否可用 → 掌握 MLP 训练的完整流程。

一、知识点 1：PyTorch 和 CUDA 的安装

1.1 先搞懂：这两个东西是干嘛的？

• PyTorch：Python 的机器学习框架，相当于 "做菜的锅碗瓢盆"------ 提供了现成的神经网络层、优化器等工具，不用你从零写代码，大大降低难度。
• CUDA ：英伟达（NVIDIA）显卡的并行计算工具，相当于 "燃气灶"------ 神经网络训练需要大量计算，用 GPU（显卡）比 CPU（电脑主机）快几十倍，CUDA 就是让 PyTorch 能调用 GPU 的 "桥梁"。

1.2 安装前的准备：确认显卡类型

只有NVIDIA（英伟达）显卡支持 CUDA，AMD 显卡用的是 ROCm（暂时不讲解）。如果没有 NVIDIA 显卡，直接装 CPU 版本的 PyTorch 即可。

1.3 步骤 1：安装 Python（必备前提）

PyTorch 基于 Python 运行，所以先装 Python：

python --version

1.4 步骤 2：安装 PyTorch（自动匹配 CUDA）

推荐用官网的命令安装，会自动匹配你的系统和 CUDA 版本，不用自己手动选：

pip3 install torch torchvision torchaudio --index-url https://download.pytorch.org/whl/cu121

备用：国内源加速安装（解决网络慢的问题）：

pip3 install torch torchvision torchaudio -i https://pypi.tuna.tsinghua.edu.cn/simple --index-url https://download.pytorch.org/whl/cu121

💡 重要：PyTorch 的安装包已经包含了 CUDA 运行时，不用自己单独装 CUDA Toolkit（除非做底层开发），零基础直接用这个就够了！

二、知识点 2：CMD 中查看显卡信息的命令

我们需要知道显卡型号、是否支持 CUDA，这两个命令足够用了：

2.1 命令 1：nvidia-smi（最实用，NVIDIA 显卡专用）

这是英伟达官方的工具，能直接看显卡型号、支持的 CUDA 版本：

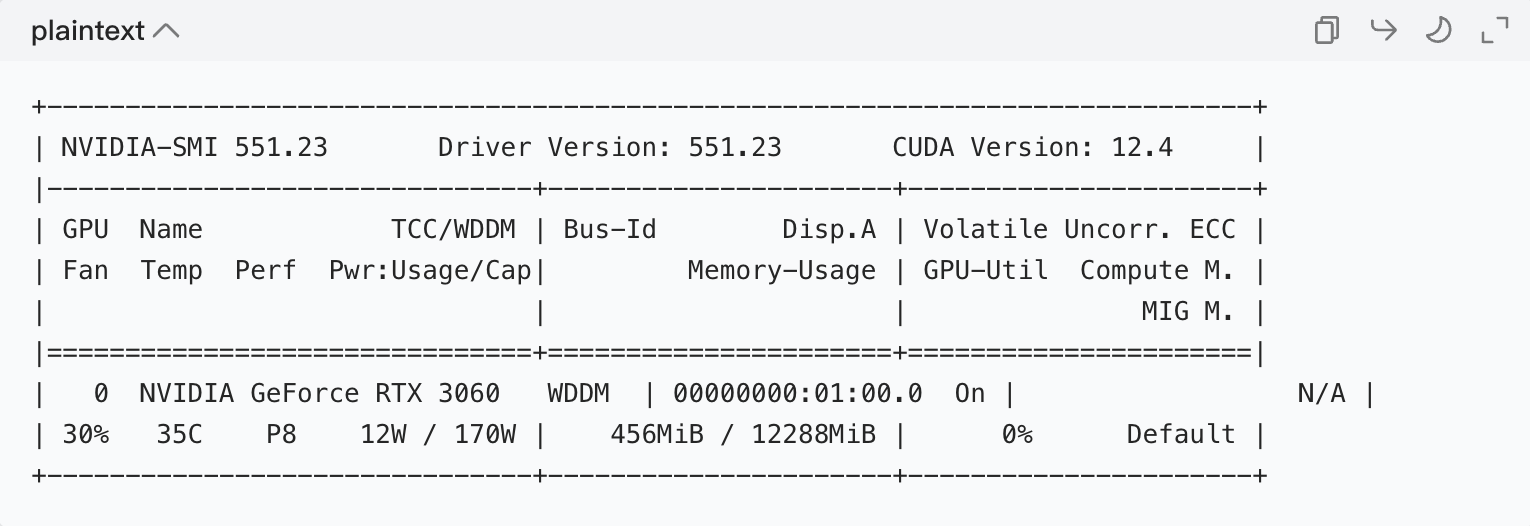
2.2 命令 2：dxdiag（Windows 自带，看所有硬件信息）

如果你的电脑没有 NVIDIA 显卡，用这个命令看显卡型号：

1. 打开 cmd，输入： dxdiag
2. 弹出 "DirectX 诊断工具"，点击显示选项卡，就能看到显卡型号和制造商。

三、知识点 3：CUDA 的检查（关键！确认 PyTorch 能调用 GPU）

安装完 PyTorch 后，必须检查是否能调用 CUDA，否则训练还是用 CPU，速度会很慢。

3.1 检查步骤

1. 打开 cmd，输入python，进入 Python 交互环境（出现>>>提示符）。
2. 逐行输入以下代码：

import torch  # 导入PyTorch库
print(torch.cuda.is_available())  # 检查CUDA是否可用（返回True/False）
print(torch.cuda.device_count())  # 查看可用的GPU数量
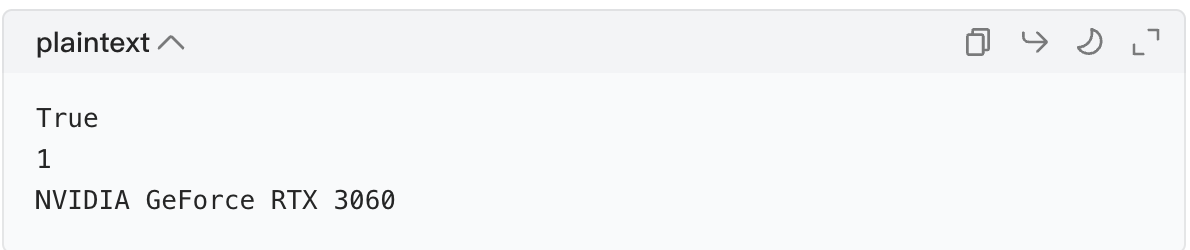
print(torch.cuda.get_device_name(0))  # 查看第一个GPU的名字

3.2 结果解读

• 如果torch.cuda.is_available()返回True：恭喜！PyTorch 能调用 GPU 了。
• 如果返回False：原因可能是：

1. 显卡不是 NVIDIA；
2. 显卡驱动没装 / 太旧；
3. PyTorch 装的是 CPU 版本。

示例输出（成功的情况）：

四、知识点 4：简单神经网络（MLP）的完整流程

这是核心内容！我们用一个简单的回归任务（预测数值）来讲解，避免一上来就用复杂的 MNIST 数据集，更容易理解。

4.1 先搞懂：MLP 是什么？

MLP（多层感知机）是最基础的神经网络，由输入层、隐藏层、输出层组成：

• 输入层：接收数据（比如我们的数据集有 2 个特征，输入层就有 2 个神经元）。
• 隐藏层：提取数据特征（比如设 10 个神经元）。
• 输出层：输出预测结果（回归任务输出 1 个数值）。

4.2 整体流程拆解

整个训练流程分为 6 个小步骤：

1. 数据预处理（归一化、转张量）
2. 定义 MLP 模型（继承 nn.Module）
3. 定义损失函数和优化器
4. 训练循环（前向传播→计算损失→反向传播→更新参数）
5. 执行训练
6. 可视化损失曲线

4.3 步骤 1：导入必要的库

首先导入代码需要的库，先记着 "这些是工具，要用的时候拿出来"：

import torch
import torch.nn as nn  # 神经网络核心库
import numpy as np     # 处理数据
import matplotlib.pyplot as plt  # 可视化损失曲线

4.4 步骤 2：数据预处理（归一化 + 转张量）

1. 先造一个简单的数据集

我们自己造一个数据集，比如：y = 2*x1 + 3*x2 + 0.5 + 少量噪声，让模型学习这个规律（比用真实数据集更易理解）。

2. 归一化：让数据 "站在同一水平线"

如果数据的数值范围相差太大（比如 x1 是 0-100，x2 是 0-1），模型学起来会很慢。归一化 就是把数据缩放到 0-1 之间，公式：(数据-最小值)/(最大值-最小值)。

3. 转张量：PyTorch 的 "专用数组"

张量（Tensor）是 PyTorch 的核心数据结构，相当于 Python 的列表 / NumPy 的数组，但能在 GPU 上运行，速度更快。

代码示例（带详细注释）：

# 1. 造数据集（固定随机种子，让结果可重复）
np.random.seed(0)
n_samples = 1000  # 1000个样本
x = np.random.rand(n_samples, 2)  # 每个样本有2个特征（x1, x2），范围0-1
# 真实的y值：2*x1 + 3*x2 + 0.5，加一点噪声让数据更接近真实情况
y = 2 * x[:, 0] + 3 * x[:, 1] + 0.5 + np.random.randn(n_samples) * 0.1

# 2. 归一化（这里x本来就是0-1，演示方法即可）
x_min = x.min(axis=0)  # 每个特征的最小值
x_max = x.max(axis=0)  # 每个特征的最大值
x_normalized = (x - x_min) / (x_max - x_min)  # 归一化后的x

# 3. 转换成PyTorch张量（float32是PyTorch常用精度，速度快）
x_tensor = torch.tensor(x_normalized, dtype=torch.float32)
# unsqueeze(1)：把y从一维(1000,)变成二维(1000,1)，和模型输出维度匹配
y_tensor = torch.tensor(y, dtype=torch.float32).unsqueeze(1)

4.5 步骤 3：定义 MLP 模型（继承 nn.Module）

这是 PyTorch 定义模型的固定套路 ：继承nn.Module类，定义层，写前向传播。

1. 核心要点

• 必须继承nn.Module：这是 PyTorch 所有模型的基类，能自动处理参数更新、GPU 迁移等。
• 全连接层（nn.Linear）：MLP 的核心层，把上一层的每个神经元和下一层的每个神经元连接。
• 激活函数（ReLU）：给模型加入非线性，让模型能学习复杂规律（没有激活函数，MLP 就和线性回归一样了）。

代码示例：

# 定义MLP模型
class MLP(nn.Module):
    def __init__(self):
        super(MLP, self).__init__()  # 继承父类的初始化方法，必须写！
        # 定义层：输入层(2维)→隐藏层(10维)→输出层(1维)
        self.fc1 = nn.Linear(2, 10)  # fc=fully connected（全连接）
        self.fc2 = nn.Linear(10, 1)
        self.relu = nn.ReLU()  # 激活函数
    
    # 定义前向传播（数据的流动路径）
    def forward(self, x):
        out = self.fc1(x)  # 输入层→隐藏层
        out = self.relu(out)  # 隐藏层加激活函数
        out = self.fc2(out)  # 隐藏层→输出层
        return out

# 实例化模型
model = MLP()
# 查看模型结构（可选）
print(model)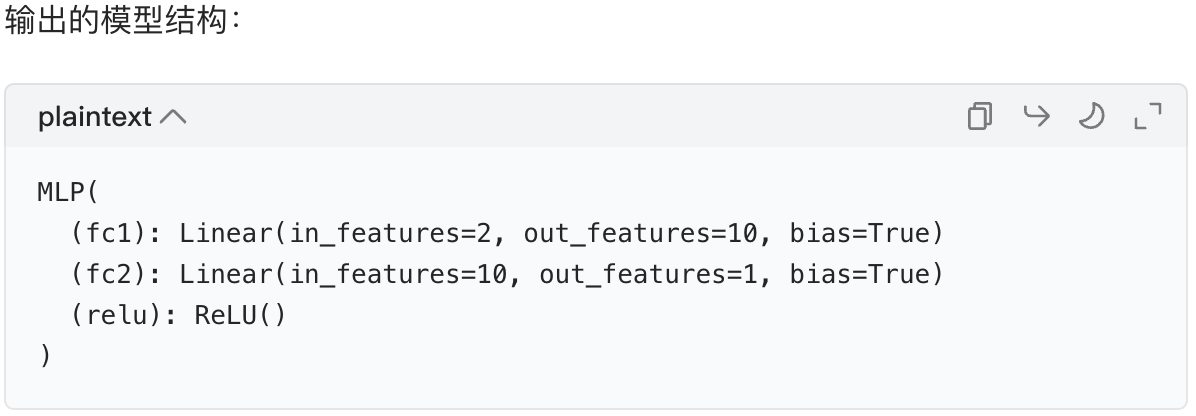

4.6 步骤 4：定义损失函数和优化器

1. 损失函数：衡量模型的 "误差"

• 回归任务（预测数值）：用均方误差（MSELoss）------ 预测值和真实值的差的平方的平均值。
• 分类任务（比如识别数字）：用交叉熵损失（CrossEntropyLoss）。

2. 优化器：让模型 "学习进步"

优化器的作用是更新模型参数 ，减小损失。常用的是Adam（比 SGD 更智能，收敛更快），需要指定：

• 模型参数（model.parameters()）：告诉优化器要更新哪些参数。
• 学习率（lr=0.01）：每次更新的步长（步长太大容易错过最优解，太小收敛太慢）。

代码示例：

 # 定义损失函数（回归用均方误差）
criterion = nn.MSELoss()

# 定义优化器（Adam优化器）
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

4.7 步骤 5：定义训练流程（训练循环）

训练的核心是重复执行 4 个动作：前向传播→计算损失→反向传播→更新参数。

1. 训练循环的核心步骤

1. 前向传播：把数据输入模型，得到预测值。
2. 计算损失：用损失函数比较预测值和真实值。
3. 清空梯度 ：optimizer.zero_grad()（PyTorch 会累积梯度，必须清空）。
4. 反向传播 ：loss.backward()（计算损失对参数的梯度）。
5. 更新参数 ：optimizer.step()（用梯度更新参数）。

代码示例：

# 训练参数
epochs = 100  # 训练轮数（把数据集看100遍）
loss_list = []  # 保存每一轮的损失，用于可视化

# 训练循环
for epoch in range(epochs):
    # 1. 前向传播：得到预测值
    y_pred = model(x_tensor)
    
    # 2. 计算损失
    loss = criterion(y_pred, y_tensor)
    
    # 3. 清空梯度（必须先做这个）
    optimizer.zero_grad()
    
    # 4. 反向传播：计算梯度
    loss.backward()
    
    # 5. 更新参数
    optimizer.step()
    
    # 保存损失值
    loss_list.append(loss.item())  # item()把张量转成普通数值
    
    # 每10轮打印一次损失，看训练进度
    if (epoch + 1) % 10 == 0:
        print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}')

4.8 步骤 6：可视化损失曲线

用matplotlib画损失随轮数变化的曲线，能直观看到模型的训练效果。

代码示例：

# 可视化损失曲线
plt.figure(figsize=(10, 6))  # 设置图片大小
plt.plot(loss_list, label='Training Loss', color='blue')  # 画曲线
plt.xlabel('Epoch')  # x轴：训练轮数
plt.ylabel('Loss')  # y轴：损失值
plt.title('MLP Training Loss Curve')  # 标题
plt.legend()  # 显示图例
plt.grid(True)  # 显示网格
plt.show()  # 显示图片

效果：曲线逐渐下降并趋于平稳，说明模型训练得很好。

4.9 额外：测试模型（看预测效果）

训练完后，用新数据测试模型，看是否能学到规律：

# 测试数据：x1=0.5，x2=0.5
test_x = torch.tensor([[0.5, 0.5]], dtype=torch.float32)
# 预测
test_y = model(test_x)
print(f'测试输入[0.5, 0.5]的预测值：{test_y.item():.4f}')

预期结果 ：真实值是2*0.5 + 3*0.5 + 0.5 = 3，预测值接近 3 就说明模型学对了（比如 2.9876）。

五、总结

今天我们学了 4 个核心知识点，串联起来就是 "环境搭建→环境检查→模型训练" 的完整流程：

1. PyTorch 和 CUDA 安装：用官网命令自动匹配，最省心。
2. 查看显卡信息 ：nvidia-smi是最实用的命令。
3. CUDA 检查 ：用torch.cuda.is_available()确认 GPU 可用。
4. MLP 训练流程：数据预处理→定义模型→损失函数 / 优化器→训练循环→可视化。

你可以把上面的代码复制到 Python 文件中（比如mlp_train.py），直接运行，看看效果。

简单神经网络流程中数据预处理的代码示例

数据预处理是神经网络训练的第一步，核心目标是让数据变成 PyTorch 能处理的格式（张量），并让数据分布更适合模型学习（比如归一化）。

下面我会分两个常见场景（回归任务、分类任务）给出完整的预处理代码，每一步都加详细注释，同时解释为什么要这么做，让你不仅会用还能理解。

先明确：数据预处理的核心步骤

不管是回归还是分类，预处理都包含这几个关键动作：

1. 数据准备（生成 / 加载原始数据）；
2. 数据清洗（本例简化，跳过缺失值 / 异常值处理）；
3. 特征缩放（归一化 / 标准化，让数据范围一致）；
4. 转换为张量（PyTorch 的核心数据结构）；
5. 划分训练集 / 测试集（用训练集学习，测试集验证效果）。

---

场景 1：回归任务的数据预处理（预测连续数值）

延续上节课的例子（预测 y = 2*x1 + 3*x2 + 0.5 + 噪声），补充训练集 / 测试集划分（更贴近真实项目）。

完整代码（带逐行解释）

# 1. 导入需要的库
import numpy as np  # 处理数值数据的基础库
import torch  # PyTorch核心库
from sklearn.model_selection import train_test_split  # 划分训练集/测试集的工具（超实用）

# 2. 生成原始数据（模拟真实场景的原始数据）
np.random.seed(0)  # 固定随机种子，让结果可重复
n_samples = 1000  # 总共1000个样本
# 生成特征：每个样本有2个特征（x1, x2），范围0~10（故意放大范围，体现归一化的重要性）
x = np.random.rand(n_samples, 2) * 10  # 形状：(1000, 2)
# 生成标签：y = 2*x1 + 3*x2 + 0.5 + 少量噪声（模拟真实的数值关系）
y = 2 * x[:, 0] + 3 * x[:, 1] + 0.5 + np.random.randn(n_samples) * 0.1  # 形状：(1000,)

# 3. 查看原始数据的基本信息（可选，帮助理解数据）
print("原始特征的形状：", x.shape)  # 输出 (1000, 2)
print("原始标签的形状：", y.shape)  # 输出 (1000,)
print("原始特征的最大值：", x.max(axis=0))  # 每个特征的最大值（比如 [9.9758, 9.9644]）
print("原始特征的最小值：", x.min(axis=0))  # 每个特征的最小值（比如 [0.0047, 0.0071]）

# 4. 划分训练集和测试集（核心！避免模型"记住"数据）
# train_test_split：把数据按7:3分成训练集（70%）和测试集（30%）
# random_state=0：固定划分方式，结果可重复
x_train, x_test, y_train, y_test = train_test_split(
    x, y, test_size=0.3, random_state=0
)

print("\n训练集特征形状：", x_train.shape)  # 输出 (700, 2)
print("测试集特征形状：", x_test.shape)    # 输出 (300, 2)

# 5. 特征缩放：归一化（Min-Max Scaling）→ 把数据缩放到0~1之间
# 为什么要做？如果x1范围是0~10，x2范围是0~1000，模型会优先学习x2，忽略x1
# 计算训练集的最大值和最小值（注意：必须用训练集的统计量，不能用测试集！避免数据泄露）
x_train_min = x_train.min(axis=0)  # 训练集每个特征的最小值
x_train_max = x_train.max(axis=0)  # 训练集每个特征的最大值

# 归一化公式：(数据 - 最小值) / (最大值 - 最小值)
x_train_normalized = (x_train - x_train_min) / (x_train_max - x_train_min)
x_test_normalized = (x_test - x_train_min) / (x_train_max - x_train_min)  # 测试集用训练集的统计量！

print("\n归一化后训练集的最大值：", x_train_normalized.max(axis=0))  # 输出 [1., 1.]
print("归一化后训练集的最小值：", x_train_normalized.min(axis=0))  # 输出 [0., 0.]

# 6. 转换为PyTorch张量（模型只能处理张量，不能处理numpy数组）
# dtype=torch.float32：PyTorch默认用32位浮点数，速度快、内存省
x_train_tensor = torch.tensor(x_train_normalized, dtype=torch.float32)
x_test_tensor = torch.tensor(x_test_normalized, dtype=torch.float32)

# 标签y是一维的，用unsqueeze(1)转成二维（匹配模型输出的维度）
# 比如从 (700,) 变成 (700, 1)
y_train_tensor = torch.tensor(y_train, dtype=torch.float32).unsqueeze(1)
y_test_tensor = torch.tensor(y_test, dtype=torch.float32).unsqueeze(1)

# 7. 查看最终的张量形状（确认维度正确）
print("\n训练集特征张量形状：", x_train_tensor.shape)  # 输出 torch.Size([700, 2])
print("训练集标签张量形状：", y_train_tensor.shape)    # 输出 torch.Size([700, 1])
print("测试集特征张量形状：", x_test_tensor.shape)     # 输出 torch.Size([300, 2])
print("测试集标签张量形状：", y_test_tensor.shape)     # 输出 torch.Size([300, 1])

关键知识点解读

为什么划分训练集 / 测试集？

就像学生学习时，用课后题（训练集）练习，用考试卷（测试集）检验真实水平，避免模型 "死记硬背" 训练数据（过拟合）。

为什么测试集要用训练集的归一化统计量？

测试集模拟的是 "未知数据"，我们在训练时不知道测试集的分布，所以必须用训练集的最大值 / 最小值，否则会引入测试集的信息，导致模型评估不准。

为什么要转二维张量？

模型的全连接层（nn.Linear）接收的是二维数据（样本数 × 特征数），标签也需要和模型输出的维度一致（比如模型输出是 (700,1)，标签也得是 (700,1)）。

---

场景 2：分类任务的数据预处理（预测离散类别）

以 手写数字识别（简化版） 为例，模拟手写数字的特征（像素值），预测数字属于 0~9 中的哪一类，更贴近实际的分类任务。

完整代码（带逐行解释）

# 1. 导入需要的库
import numpy as np
import torch
from sklearn.model_selection import train_test_split

# 2. 生成原始数据（模拟手写数字数据：28×28像素=784个特征，10个类别）
np.random.seed(0)
n_samples = 500  # 500个样本
n_features = 28*28  # 每个样本784个特征（模拟28×28像素）
n_classes = 10  # 0~9共10个类别

# 生成特征：像素值范围0~255（模拟灰度图像的像素值）
x = np.random.randint(0, 256, size=(n_samples, n_features))  # 形状：(500, 784)
# 生成标签：0~9的随机整数（模拟数字类别）
y = np.random.randint(0, n_classes, size=(n_samples,))  # 形状：(500,)

# 3. 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(
    x, y, test_size=0.3, random_state=0
)

# 4. 特征缩放：标准化（Z-Score Normalization）→ 让数据服从均值为0、方差为1的分布
# 分类任务中标准化也很常用，尤其是图像数据
# 计算训练集的均值和方差
x_train_mean = x_train.mean(axis=0)  # 每个特征的均值
x_train_std = x_train.std(axis=0)    # 每个特征的方差

# 标准化公式：(数据 - 均值) / 方差（避免除以0，加一个极小值1e-8）
x_train_standardized = (x_train - x_train_mean) / (x_train_std + 1e-8)
x_test_standardized = (x_test - x_train_mean) / (x_train_std + 1e-8)

# 5. 转换为PyTorch张量
# 特征张量：float32类型
x_train_tensor = torch.tensor(x_train_standardized, dtype=torch.float32)
x_test_tensor = torch.tensor(x_test_standardized, dtype=torch.float32)

# 分类任务的标签：long类型（整数），不需要转二维（CrossEntropyLoss会自动处理）
y_train_tensor = torch.tensor(y_train, dtype=torch.long)
y_test_tensor = torch.tensor(y_test, dtype=torch.long)

# 6. 查看最终张量形状
print("训练集特征张量形状：", x_train_tensor.shape)  # 输出 torch.Size([350, 784])
print("训练集标签张量形状：", y_train_tensor.shape)    # 输出 torch.Size([350])
print("测试集特征张量形状：", x_test_tensor.shape)     # 输出 torch.Size([150, 784])
print("测试集标签张量形状：", y_test_tensor.shape)     # 输出 torch.Size([150])

分类任务预处理的特殊点

1. 标签类型 ：分类任务的标签需要是torch.long（整数类型），因为 PyTorch 的交叉熵损失函数要求标签是整数类别。
2. 标准化 vs 归一化 ：图像数据常用标准化（Z-Score），也可以用归一化（把 0~255 缩放到 0~1），效果差不多，选一种即可。
3. 特征维度：手写数字的 28×28 像素展平成 784 个特征，是 MLP 处理图像的常用方式（CNN 会保留二维结构，后续再学）。

---

预处理代码的复用技巧（零基础也能快速套用）

把预处理封装成简单的函数，以后换数据时直接调用，不用重复写代码：

def preprocess_regression_data(x, y, test_size=0.3):
    """
    回归任务的预处理函数
    :param x: 原始特征（numpy数组）
    :param y: 原始标签（numpy数组）
    :param test_size: 测试集比例
    :return: 处理后的张量（x_train, x_test, y_train, y_test）
    """
    # 划分数据集
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=test_size, random_state=0)
    # 归一化
    x_train_min = x_train.min(axis=0)
    x_train_max = x_train.max(axis=0)
    x_train_norm = (x_train - x_train_min) / (x_train_max - x_train_min)
    x_test_norm = (x_test - x_train_min) / (x_train_max - x_train_min)
    # 转张量
    x_train_tensor = torch.tensor(x_train_norm, dtype=torch.float32)
    x_test_tensor = torch.tensor(x_test_norm, dtype=torch.float32)
    y_train_tensor = torch.tensor(y_train, dtype=torch.float32).unsqueeze(1)
    y_test_tensor = torch.tensor(y_test, dtype=torch.float32).unsqueeze(1)
    return x_train_tensor, x_test_tensor, y_train_tensor, y_test_tensor

# 调用函数（直接用之前的x和y）
x_train, x_test, y_train, y_test = preprocess_regression_data(x, y)

总结

数据预处理的核心就是让数据 "适配" 模型：

1. 用归一化 / 标准化让数据分布更友好；
2. 转张量让 PyTorch 能处理；
3. 划分训练集 / 测试集让模型能被正确评估。

你可以把上面的代码复制到 Python 文件中运行，观察每一步的输出变化，就能直观理解预处理的作用。

简单神经网络流程中可视化 loss 过程的代码示例

可视化 Loss（损失）曲线是神经网络训练中非常重要的一步，它能直观反映模型的学习效果：比如 Loss 是否在下降、是否过拟合、训练是否收敛等。

下面我会基于之前的MLP 回归任务 ，先给出基础的训练 Loss 可视化 ，再升级为训练 + 测试 Loss 双曲线可视化（更贴近真实项目），每一步都加详细注释，同时讲解画图的核心逻辑和 Loss 曲线的解读方法。

---

核心逻辑回顾

可视化 Loss 的关键只有两点：

1. 收集 Loss 值：在训练循环中，把每一轮的 Loss 值保存到列表里；
2. 用 Matplotlib 画图：把列表中的 Loss 值按训练轮数（Epoch）绘制成曲线。

---

场景 1：基础版 ------ 仅可视化训练 Loss

完整代码（可直接运行）

# 1. 导入必要的库
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt  # 绘图核心库
from sklearn.model_selection import train_test_split

# 2. 生成数据并预处理（复用之前的回归数据）
np.random.seed(0)
n_samples = 1000
x = np.random.rand(n_samples, 2) * 10  # 特征：2维，范围0~10
y = 2 * x[:, 0] + 3 * x[:, 1] + 0.5 + np.random.randn(n_samples) * 0.1  # 标签

# 划分训练集/测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=0)

# 归一化
x_train_min = x_train.min(axis=0)
x_train_max = x_train.max(axis=0)
x_train_norm = (x_train - x_train_min) / (x_train_max - x_train_min)
x_test_norm = (x_test - x_train_min) / (x_train_max - x_train_min)

# 转张量
x_train_tensor = torch.tensor(x_train_norm, dtype=torch.float32)
x_test_tensor = torch.tensor(x_test_norm, dtype=torch.float32)
y_train_tensor = torch.tensor(y_train, dtype=torch.float32).unsqueeze(1)
y_test_tensor = torch.tensor(y_test, dtype=torch.float32).unsqueeze(1)

# 3. 定义MLP模型
class MLP(nn.Module):
    def __init__(self):
        super(MLP, self).__init__()
        self.fc1 = nn.Linear(2, 10)
        self.fc2 = nn.Linear(10, 1)
        self.relu = nn.ReLU()
    
    def forward(self, x):
        out = self.fc1(x)
        out = self.relu(out)
        out = self.fc2(out)
        return out

model = MLP()

# 4. 定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

# 5. 训练模型并收集Loss值
epochs = 100  # 训练轮数
train_loss_list = []  # 空列表，用于保存每一轮的训练Loss

for epoch in range(epochs):
    # 训练模式（虽然本例没有Dropout/BatchNorm，但是好习惯）
    model.train()
    
    # 前向传播
    y_pred = model(x_train_tensor)
    
    # 计算损失
    loss = criterion(y_pred, y_train_tensor)
    
    # 反向传播和参数更新
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    # 保存当前轮的Loss值（item()把张量转成普通数值）
    train_loss_list.append(loss.item())
    
    # 每10轮打印一次Loss，观察训练进度
    if (epoch + 1) % 10 == 0:
        print(f'Epoch [{epoch+1}/{epochs}], Train Loss: {loss.item():.4f}')

# 6. 可视化训练Loss曲线（核心部分）
plt.figure(figsize=(10, 6))  # 设置图片大小：宽10英寸，高6英寸
plt.plot(train_loss_list, label='Training Loss', color='blue', linewidth=2)  # 画Loss曲线

# 添加图表标签和标题（让图更易读）
plt.xlabel('Epoch', fontsize=12)  # x轴标签：训练轮数
plt.ylabel('Loss', fontsize=12)    # y轴标签：损失值
plt.title('MLP Training Loss Curve', fontsize=14)  # 图表标题
plt.legend(fontsize=12)  # 显示图例（对应label='Training Loss'）
plt.grid(True, alpha=0.3)  # 显示网格（alpha=0.3让网格更淡，不刺眼）
plt.show()  # 显示图片

代码解读（画图核心函数）

函数	作用
plt.figure(figsize=(10,6))	创建画布，设置大小（宽 × 高）
plt.plot(列表, label, color)	绘制折线图，label是图例名称，color是颜色
plt.xlabel/ylabel	设置 x/y 轴的名称
plt.title	设置图表标题
plt.legend()	显示图例（对应plot中的label）
plt.grid(True)	显示网格，方便看数值
plt.show()	弹出窗口显示图片

运行效果

场景 2：进阶版 ------ 训练 Loss + 测试 Loss 双曲线可视化

在真实项目中，我们不仅要关注训练 Loss，还要看测试 Loss：

• 如果训练 Loss 下降，测试 Loss 也下降并趋于平稳：模型泛化能力好；
• 如果训练 Loss 持续下降，测试 Loss 反而上升：模型过拟合（死记硬背训练数据，不会举一反三）。

完整代码（可直接运行）

# 前面的导入库、数据预处理、模型定义部分和基础版一致，这里省略（可直接复制基础版的前4步）
# 直接从训练部分开始

# 5. 训练模型并收集训练+测试Loss值
epochs = 100
train_loss_list = []  # 训练Loss列表
test_loss_list = []   # 测试Loss列表

for epoch in range(epochs):
    # ---------------------- 训练阶段 ----------------------
    model.train()  # 训练模式（启用Dropout/BatchNorm）
    y_pred_train = model(x_train_tensor)
    train_loss = criterion(y_pred_train, y_train_tensor)
    
    optimizer.zero_grad()
    train_loss.backward()
    optimizer.step()
    
    # ---------------------- 测试阶段 ----------------------
    model.eval()  # 评估模式（禁用Dropout/BatchNorm，避免影响测试结果）
    with torch.no_grad():  # 禁用梯度计算（测试时不需要，加快速度、节省内存）
        y_pred_test = model(x_test_tensor)
        test_loss = criterion(y_pred_test, y_test_tensor)
    
    # ---------------------- 保存Loss ----------------------
    train_loss_list.append(train_loss.item())
    test_loss_list.append(test_loss.item())
    
    # 每10轮打印一次
    if (epoch + 1) % 10 == 0:
        print(f'Epoch [{epoch+1}/{epochs}], Train Loss: {train_loss.item():.4f}, Test Loss: {test_loss.item():.4f}')

# 6. 可视化训练+测试Loss双曲线
plt.figure(figsize=(10, 6))
# 画训练Loss曲线
plt.plot(train_loss_list, label='Training Loss', color='blue', linewidth=2)
# 画测试Loss曲线
plt.plot(test_loss_list, label='Testing Loss', color='red', linewidth=2, linestyle='--')  # 虚线区分

# 添加标签和标题
plt.xlabel('Epoch', fontsize=12)
plt.ylabel('Loss', fontsize=12)
plt.title('MLP Training and Testing Loss Curve', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True, alpha=0.3)
plt.show()

关键新增知识点

运行效果

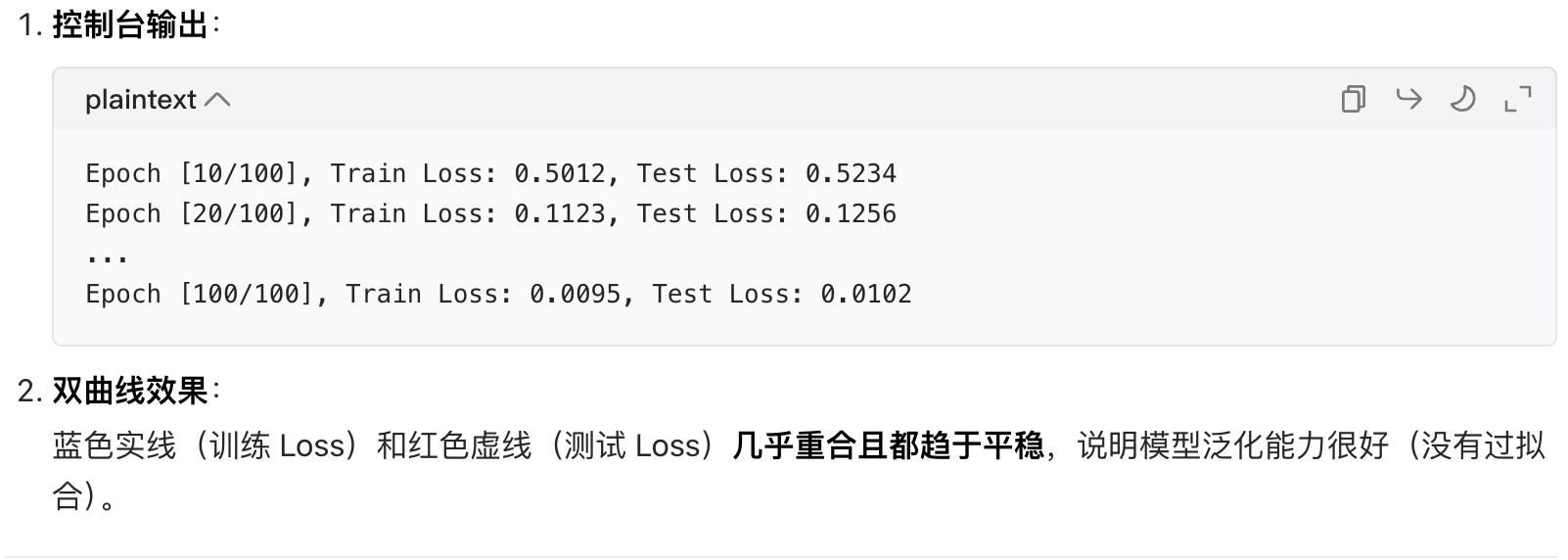
场景 3：分类任务的 Loss 可视化（扩展）

如果是分类任务（比如手写数字识别），Loss 可视化的代码完全一样 ，只是损失函数换成nn.CrossEntropyLoss()，标签类型为torch.long。这里给出核心差异部分：

# 分类任务的损失函数
criterion = nn.CrossEntropyLoss()

# 训练循环中收集Loss的逻辑和回归任务完全一致
train_loss_list = []
test_loss_list = []

for epoch in range(epochs):
    # 训练阶段
    model.train()
    y_pred_train = model(x_train_tensor)
    train_loss = criterion(y_pred_train, y_train_tensor)  # y_train_tensor是long类型
    
    # 反向传播和更新（和之前一致）
    
    # 测试阶段
    model.eval()
    with torch.no_grad():
        y_pred_test = model(x_test_tensor)
        test_loss = criterion(y_pred_test, y_test_tensor)
    
    # 保存Loss（和之前一致）

Loss 曲线的常见情况及解读（重要！）

通过 Loss 曲线能快速判断模型训练的问题，这是零基础也需要掌握的核心能力：

曲线情况	说明	解决办法
训练 Loss 持续下降，测试 Loss 也下降并平稳	理想情况，模型学习良好	继续训练或停止训练
训练 Loss 持续下降，测试 Loss 先降后升	过拟合（模型记住训练数据，泛化差）	增加数据量、用 Dropout、L2 正则化
训练 Loss 和测试 Loss 都很高且不下降	欠拟合（模型太简单，学不会规律）	增加模型层数 / 神经元数、延长训练时间
训练 Loss 波动很大	学习率太大（步长太大，错过最优解）	减小学习率（比如从 0.01 降到 0.001）
训练 Loss 上升	学习率过大或模型结构有问题	检查学习率和模型定义

美化图表的小技巧（可选）

如果想让图表更专业，可以添加这些细节：

# 调整字体（解决中文乱码问题）
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用黑体显示中文
plt.rcParams['axes.unicode_minus'] = False    # 解决负号显示问题

# 自定义刻度大小
plt.xticks(fontsize=10)
plt.yticks(fontsize=10)

# 保存图片（避免截图模糊）
plt.savefig('loss_curve.png', dpi=300, bbox_inches='tight')  # dpi=300是高清分辨率

总结

可视化 Loss 的代码非常固定 ，核心就是收集 Loss 值→用 plt.plot 画图：

1. 基础版：只画训练 Loss，适合入门；
2. 进阶版：画训练 + 测试 Loss，适合真实项目；
3. 关键技巧：测试时用model.eval()和torch.no_grad()，保证结果准确。

你可以把代码复制到 Python 文件中运行，观察 Loss 曲线的变化，结合解读方法判断模型的训练效果。

作业：今日的代码，要做到能够手敲。这已经是最简单最基础的版本了。

浙大疏锦行