浅谈：算法中的斐波那契数（六）

方法五：矩阵求幂

斐波那契数列矩阵方程：

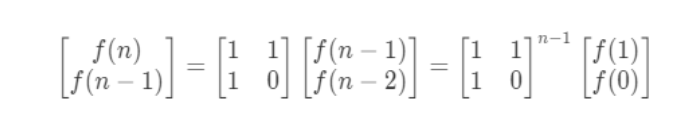
算法：

• 若 N 小于等于 1，则返回 N。
• 使用递归函数matrixPower 计算给定矩阵 A 的幂。幂为 N-1，其中 N 是第 N 个 斐波那契数。
• matrixPower 函数将对 N/2 个斐波那契数进行操作。
• 在 matrixPower 中，调用 multiply 函数将两个矩阵相乘。
• 完成计算后，返回 A00 得到第 N 个斐波那契数。

Java 实现

class Solution {
    int fib(int N) {
        if (N <= 1) {
          return N;
        }
        int[][] A = new int[][]{{1, 1}, {1, 0}};
        matrixPower(A, N-1);

        return A[0][0];
    }

    void matrixPower(int[][] A, int N) {
        if (N <= 1) {
          return;
        }
        matrixPower(A, N/2);
        multiply(A, A);

        int[][] B = new int[][]{{1, 1}, {1, 0}};
        if (N%2 != 0) {
            multiply(A, B);
        }
    }

    void multiply(int[][] A, int[][] B) {
        int x = A[0][0] * B[0][0] + A[0][1] * B[1][0];
        int y = A[0][0] * B[0][1] + A[0][1] * B[1][1];
        int z = A[1][0] * B[0][0] + A[1][1] * B[1][0];
        int w = A[1][0] * B[0][1] + A[1][1] * B[1][1];

        A[0][0] = x;
        A[0][1] = y;
        A[1][0] = z;
        A[1][1] = w;
    }
}

复杂度分析