【力扣刷题笔记-在排序数组中查找元素的第一个和最后一个位置】

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

分析：

这一题属于查找算法，要实现的是找第一个target的位置和最后一个target的位置，因为题目还要求了时间复杂度为O(log n)，所以考虑用二分查找。

先看一下普通二分查找的实现：

cpp 复制代码

int binarySearch(vector<int>& nums, int target) {
    int left = 0, right = nums.size() - 1;

    while (left <= right) {
        int mid = left + (right - left) / 2;

        if (nums[mid] == target) {
            return mid;              // 找到了，直接返回
        } else if (nums[mid] < target) {
            left = mid + 1;          // target 在右边
        } else {
            right = mid - 1;         // target 在左边
        }
    }

    return -1; // 没找到
}

这里是用mid来标记target的位置，如果找到了，就返回这个位置。

但是我们现在要找的是第一个和最后一个target，所以必须要查找两次。第一次去找第一个target，也就是左边界。第二次去找最后一个target，也就是右边界。现在就要利用二分查找的思想去解决这个问题，但跟普通的二分查找稍有不同。

一、左边界查找

在找左边界的时候，用left和right来指向数组，不断移动来逼近这个左边界。关键代码是这个：

cpp 复制代码

if (nums[mid] >= target)
    right = mid - 1;
else
    left = mid + 1;

普通二分查找的时候，当nums[mid] == target的时候就可以直接返回了，但是现在不行，因为即使找到了一个也得继续向前寻找看是不是还有其他相等的数，所以nums[mid] >= target的时候，都得移动right去向前查找。当nums[mid] < target 时，left 才会右移到mid + 1，这时mid左边的所有位置，已经全部被确认 < target，那么不管如何移动，left也保证了它左边的所有数肯定都会 < target，这样，在循环结束之后，left 一定会指向第一个 ≥ target 的位置。也就是说，如果有 target，它只能从 left 开始。再去判断left这个位置是不是真的等于 target，是的话就可以直接返回，如果不是，说明这个数不存在，直接返回 [-1, -1]。

举个例子：

nums = [1, 2, 4, 4, 4, 4, 6, 7, 9, 10, 12]

target = 4

初始：left = 0，right = 10。这时我们认为第一个 4 可能在整个区间里。

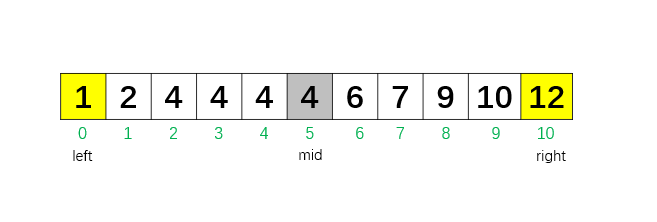
第 1 次循环：mid = 5，nums[5] = 4。因为 nums[5] ≥ 4，所以把 right 移到 mid - 1 = 4，继续在左边找更靠前的位置。

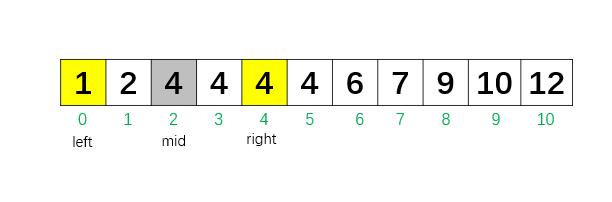
第 2 次循环：left = 0，right = 4，mid = 2，nums[2] = 4。因为 nums[2] ≥ 4，所以把 right 移到 mid - 1 = 1，也就是第一个 4 不可能在位置 2 的右边，那么继续收缩边界。

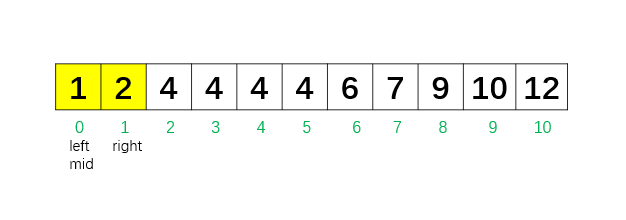
第 3 次循环：left = 0，right = 1，mid = 0，nums[0] = 1。因为 nums[0] < 4，所以把 left 移到 mid + 1 = 1，说明第一个 4 得往右找找了。

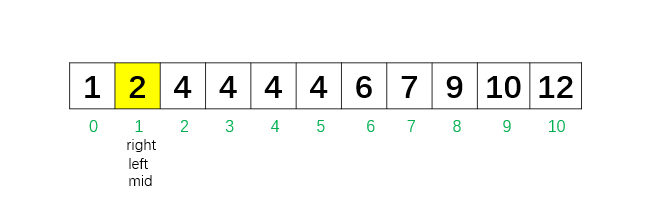
第 4 次循环：left = 1，right = 1，mid = 1，nums[1] = 2。因为 nums[1] < 4，所以把 left 移到 mid + 1 = 2，继续排除小于 4 的位置。

这时，left = 2，right = 1，循环结束。此时left 已经越过 right，说明 left 正好指向第一个 ≥ 4 的位置，把这个位置存下来。

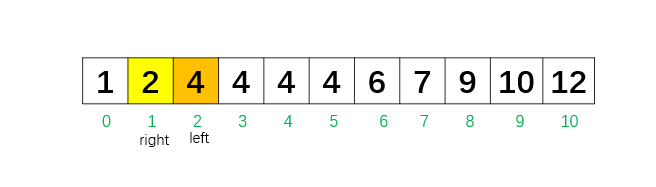
然后比较nums[left]和target的值，恰好相等，则这个位置就是第一个target的位置。

二、右边界查找

这里就和找左边界类似，重新设置初始left = 0，right = 10。

对称的代码如下：

cpp 复制代码

if (nums[mid] <= target)
    left = mid + 1;
else
    right = mid - 1;

概括下找右边界的过程：

遇到 ≤ target 就右移 left，

遇到 > target 就左移 right，

循环结束时 right 就是最后一个 target

初始时left = 0，right = 10，可能的最后一个 4 在整个数组里。

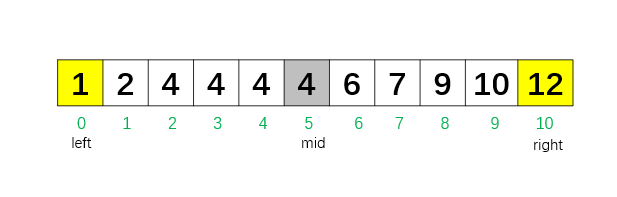
第 1 次循环：mid = 5，nums[5] = 4 ，nums[mid] <= target，这里还是 4，但不确定是不是最后一个，所以向右继续找，把 left 移到 mid + 1 = 6。

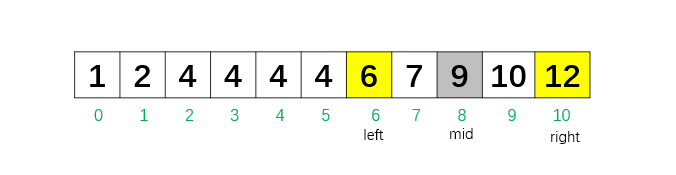
第 2 次循环：left = 6，right = 10，mid = 8，nums[8] = 9，因为 nums[mid] > target，所以把 right 移到 mid - 1 = 7

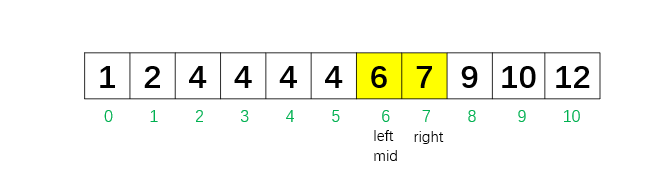
第 3 次循环：left = 6，right = 7，mid = 6，nums[6] = 6。因为 nums[mid] > target，所以把 right 再移到 mid - 1 = 5，继续向左收缩范围。

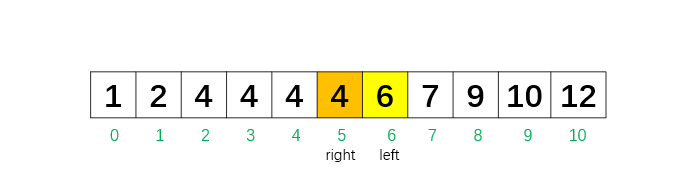
left = 6，right = 5。 left 已越过 right，说明 right 停在"最后一个 ≤ 4"的位置，也就是最后一个 4。

最终合并代码如下：

cpp 复制代码

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
    int n = nums.size();
    if(n==0)
      return {-1,-1};
    //找左边界
    int left = 0;
    int right = n - 1;
    while(left<=right){
        int mid = left + (right - left) / 2;
        if(nums[mid]>=target)
          right=mid-1;
        else
          left=mid+1;
        }
    if(left==n||nums[left]!=target)//找不到的情况
      return {-1,-1};
    //找右边界
    int a = left;
    left = 0;
    right = n - 1;
    while(left<=right){
        int mid = left + (right - left) / 2;
        if(nums[mid]<=target)
          left=mid+1;
        else
          right=mid-1;
        }
    int b=right;
    return{a,b};
   }
};

此外，target 在不在数组里，只需要判断一次，在找左边界的时候判断。前面已经介绍过，循环结束之后，left 一定会指向第一个 ≥ target 的位置，那么左边界查找最终可能会出现这几种情况：

左边界结果	含义
`left == n`	所有数都 < target → target 不存在
`nums[left] > target`	target 落在空隙里 → 不存在
`nums[left] == target`	target 存在，left 是起点

这些情况在代码中都已经完全覆盖到了。由于左边界已经判断过 target 是否存在，如果不存在，函数会 return，根本走不到右边界。所以找右边界时，默认 target 已经存在，所以不需要再判断。