【LeetCode 958】判定完全二叉树:警惕 BFS 中的"管中窥豹"陷阱
在二叉树的面试题中,判定完全二叉树(Check Completeness of a Binary Tree)是一道考察层序遍历(BFS)细节处理的经典题目。
很多同学知道这道题要用队列(Queue)做 BFS,但在处理"何时结束"、"如何判定失败"的逻辑上,很容易掉进思维陷阱。
今天我们就通过两段代码的对比(一段 100% 通过,一段 95% 通过),来揭示算法设计中的局部视野 vs 全局视野 的差异。
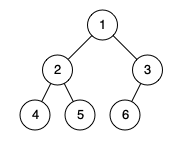
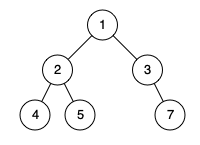
1. 题目核心难点
完全二叉树的定义通俗来说就是:
- 前面的层必须是满的。
- 最后一层的节点必须紧凑地靠左排列。
- 中间不能有空洞。
这意味着,如果我们对树进行层序遍历(BFS),将所有节点(包括空节点 null)按顺序放入队列。那么,一旦出现了第一个 null,后面就绝对不能再出现任何非 null 的节点。如果出现了,说明树中间断开了,不是完全二叉树。
2. 案例分析:为什么代码 2 只能通过 95%?
让我们先来看看这段"差一点就对了"的代码(Code 2)。它的思路看起来很机智:在遍历过程中,盯着当前节点和下一个节点看。
❌ Code 2(存在逻辑漏洞)
java
class Solution {
public boolean isCompleteTree(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()){
TreeNode cur = queue.poll();
// 试图通过"当前节点"和"下一个节点(peek)"的关系直接下定论
if(cur == null && queue.peek() != null) return false; // 漏洞 1
if(cur == null && queue.peek() == null) return true; // 漏洞 2 (致命)
// 注意:这里其实还会抛出空指针异常,因为当 cur 为 null 时,
// 下面的代码会尝试 cur.left,虽然题目可能保证了数据,但在逻辑上是不严谨的。
// 假设我们忽略空指针问题,只看逻辑:
if(cur != null) {
queue.offer(cur.left);
queue.offer(cur.right);
}
}
return true;
}
}致命死穴:管中窥豹(局部视野)
这段代码最大的问题在于这句话:
if(cur == null && queue.peek() == null) return true;
它的逻辑是 :如果我是空的,而且我后面排队的那个人也是空的,那肯定结束了,返回 true。
反例打击 :
假设树的层序结构是:[Node, null, null, Node]。
这显然不是完全二叉树(中间缺了两个)。
当代码执行到第一个 null 时:
cur是null。queue.peek()是第二个null。- 代码直接判定
return true。
只要连着出现两个空节点,代码 2 就会误判为"通过",完全忽略了队列后面可能还藏着一个非空的节点! queue.peek() 只能看一眼下一个,看不到队尾,这就是典型的"局部视野"导致的错误。
3. 优秀解法:全局扫视(Code 1)
来看看那段完美通过的代码(Code 1)。它的思路非常稳健:分为两个阶段。
✅ Code 1(标准答案)
java
class Solution {
public boolean isCompleteTree(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
// 阶段一:无脑入队,直到遇到第一个 null
while(!queue.isEmpty()){
TreeNode cur = queue.poll();
if(cur != null) {
// 关键点:不管孩子是不是 null,都放进去!
// 这保证了队列里完整保留了树的结构(包括空位)
queue.offer(cur.left);
queue.offer(cur.right);
} else {
// 遇到了第一个空节点,阶段一结束!
break;
}
}
// 阶段二:排查剩余队列
// 既然已经遇到了空节点,那么如果这棵树是完全的,
// 队列里剩下的所有东西必须全都是 null。
// 只要发现任何一个活着的节点,直接判死刑。
while(!queue.isEmpty()){
if(queue.peek() != null){
return false;
}
queue.poll();
}
return true;
}
}为什么 Code 1 更优?
-
逻辑分层清晰:
- 前半场:正常遍历,一旦遇到空节点,立刻停止"生成新节点"的操作。
- 后半场:专门负责"验尸"。检查剩下的队列是否纯净(全空)。
-
全局视野 :
它没有在遇到
null时急着下结论,而是用第二个while循环把队列彻底检查一遍。这就避免了"连续两个 null 后面藏着一个 Node"的坑。 -
数据结构的正确使用 :
它利用了队列 FIFO 的特性,把二叉树拉成了一维的线性结构。判定完全二叉树,本质上就是看这个线性结构中,所有的
null是否都集中在最后面。[Node, Node, Node, null, null]-> ✅ 是[Node, null, Node, null]-> ❌ 否[Node, null, null, Node]-> ❌ 否(Code 2 会挂在这里)
4. 总结
在解决 BFS 相关题目时,我们要格外注意状态的连续性。
- Code 2 的失败 在于试图用 O(1)O(1)O(1) 的视野(peek)去推断 O(N)O(N)O(N) 的结局,犯了"急于求成"的错误。
- Code 1 的成功 在于它捕捉到了完全二叉树的本质特征:"遇到空节点后,后续必须全为空",并用两个循环严谨地实现了这个逻辑。
写算法题时,不要只盯着眼前的 peek(),要想到队列深处可能还藏着"魔鬼"。