MobileMamba中的小波分析

MobileMamba中的小波分析

今天探讨一下CVPR2025中的一篇paper:MobileMamba: Lightweight Multi-Receptive Visual Mamba Network 。这项研究突破性地解决了移动设备上视觉 AI 领域的两大难题：速度（高吞吐量）与精度（高性能）的平衡。

挑战：为什么让 AI 视觉"又快又好"这么难？

在过去，主流的轻量级视觉模型主要有两类，但它们都有局限性：

1. 卷积神经网络 ：它们擅长处理局部信息，但感受野（视野范围）有限**，难以捕捉图像的长距离依赖性（比如画面最左边和最右边的物体关系）。
2. Transformer：它们能建立全局视野 ，但计算复杂度是平方级的，在处理高清大图时，计算量会急剧膨胀，速度很慢。

而近两年火起来的 Mamba 模型 ，虽然利用线性计算复杂度 解决了全局建模的效率问题，但现有的轻量级 Mamba 模型往往推理速度较慢（吞吐量不足），性能也不尽如人意。

MobileMamba 的核心突破：速度与视野的双重飞跃

MobileMamba 的目标是：在保持 Mamba 的全局建模优势的同时，彻底解决它的"慢速"瓶颈，并进一步优化视觉感知能力。

他们的解决方案是围绕一个创新模块和一个优化架构展开的：

1. 核心模块：多感受野特征交互 (MRFFI)

MobileMamba 的创新都集中在一个叫 MRFFI（Multi-Receptive Field Feature Interaction）的模块中。这个模块巧妙地将输入特征沿着通道维度分成了三股"力量"同时处理：

• 全局 Mamba + 小波增强（WTE-Mamba）

◦ 全局视野 ：使用 Mamba 模块进行双向扫描，捕捉图像的长距离依赖信息 （全局特征xmOx_{m}^{O}xmO）。

◦ 高效细节捕获 ：引入了小波变换 (WT) 和逆小波变换 (IWT) 的机制。小波变换能将图像分解为低频（主体结构）和**高频（边缘细节）**信息。关键在于，通过在尺寸减半的小波特征图上进行卷积，再恢复尺寸，有效感受野（ERF）实现了加倍，从而在不增加太多计算量的情况下，同时增强了模型对高频边缘细节的提取和视野范围。

• 多核深度卷积 (MK-DeConv) ：使用局部卷积操作（例如 k =3）来捕获多尺度的局部信息。

• 冗余消除（Identity Mapping） ：对于剩下的特征通道，直接采用恒等映射，跳过计算，从而减少高维空间中的冗余，大幅提升运行效率。

通过这种三合一的 MRFFI 模块，MobileMamba 成功实现了全局视野 与多尺度局部细节 的完美融合，并被验证拥有一个更大、更集中的有效感受野 (ERF)（如图所示）

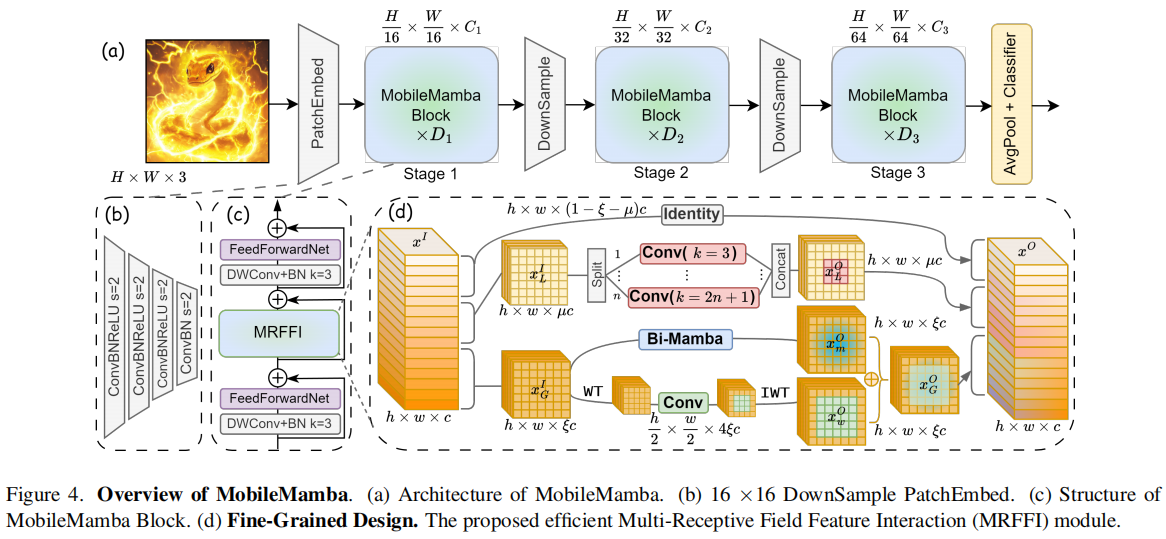
2. 宏观架构与策略优化

为了进一步提速和提效，MobileMamba 还采用了以下工程策略：

• 三阶段网络结构 ：实验证明，相比常用的四阶段网络，采用三阶段网络结构在相似吞吐量下能实现更高的精度，或者在相同性能下具有更高的吞吐量，显著增强推理速度。

• 训练策略 ：使用知识蒸馏 (KD) 让小模型向强大的教师模型学习，并将训练周期延长至 1000 个 Epoch，以充分挖掘模型潜力。

• 测试提速 ：在推理阶段，应用归一化层融合 (NLF) 技术，减少网络层数，直接加速前向传播速度。

性能数据：快了 21 倍，精度创新高！

MobileMamba 的实验结果令人惊叹，它在效率和准确性方面均超越了现有最先进的轻量级模型：

性能指标	MobileMamba 的优势
整体精度	ImageNet-1K 分类任务中，Top-1 准确率高达 83.6%。
Mamba 速度对比	在 GPU 吞吐量上，比先前的 Mamba 模型 LocalVim 快了 ×21 倍，同时 Top-1 准确率提高了 +0.7。
Mamba 精度对比	比 EfficientVMamba 快了 ×3.3 倍，同时 Top-1 准确率提高了 +2.0。
下游任务	在目标检测（RetinaNet）中，吞吐量比 EfficientVMamba 高出 ×4.3 倍，同时 mAP提高了 +2.1。

MRFFI 模块洞察

MRFFI是模型的核心，的原理可分解为以下三个组成部分：

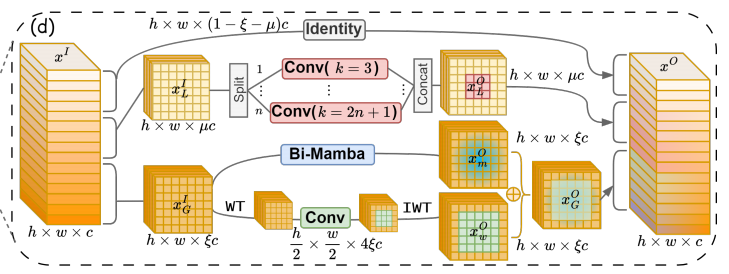
论文明确说：MRFFI 放在每个 MobileMamba block 里，用一个**高效的"多感受野特征交互"**结构，把输入特征 沿通道维切成三份，分别走三条路：WTE-Mamba（全局+小波）、MK-DeConv（多感受野局部卷积）、Identity（消冗余提速）。

(A) 通道三分：全局 / 局部 / 直连

输入特征 xI∈Rh×w×cx^I\in\mathbb{R}^{h\times w\times c}xI∈Rh×w×c，切出 ξc\xi cξc 通道做全局（global）建模（ξ\xiξ 是 global channel proportion），再切出 μc\mu cμc 通道做局部（local）多感受野卷积（μ≤1−ξ\mu\le 1-\xiμ≤1−ξ），剩下 (1−ξ−μ)c(1-\xi-\mu)c(1−ξ−μ)c 通道直接 Identity，用来减少高维空间的冗余与计算量、提高速度。

(B) WTE-Mamba：全局建模 + 小波增强高频细节

论文对 WTE-Mamba 的目的描述得很直白：在全局建模基础上增强高频边缘信息，同时利用 WT 后"尺度减半再卷积"的性质扩大 ERF。并且它给出关键融合公式：全局分支输出 = Mamba 输出 + 小波分支重构输出：

xGO=xmO+xwOx_G^O=x_m^O+x_w^OxGO=xmO+xwO

小波细节的机制也说得很清楚：WT 产生 1 个低频 + 3 个高频子带；在尺寸减半的特征图上卷积后，再 IWT 回到原尺寸，从而有效扩大感受野并增强边缘细节。

© MK-DeConv：多核深度可分离卷积（多感受野局部信息）

论文写法是把局部通道再分成 n 份，每份用不同 kernel 做 depthwise conv，然后 concat 起来形成 xLOx_L^OxLO。但在消融里作者也说：n=1（只用一个卷积核）效果差不多，所以最终采用 n=1 简化实现。

(D) Identity：消除通道冗余，提速

最后剩余通道直接 identity，减少不必要计算，提高处理速度。

MRFFI 的"交互"到底体现在哪？

"Interaction"不是指三段之间做复杂 attention，而是更工程化的交互方式：

在同一个 block 内同时获得：

• 全局（Mamba）+ 高频细节增强（Wavelet）
• 局部（Depthwise conv）
• 直连（Identity）

通过 Concat 在通道维融合成一个整体输出（论文给了 concat 形式的输出表达）。

WTE-Mamba代码

WTE-Mamba 的代码主体：MBWTConv2d

初始化里：两条分支的构建

(A) 小波分支需要的固定滤波器 + WT/IWT 函数

self.wt_filter, self.iwt_filter = create_wavelet_filter(wt_type, in_channels, in_channels, torch.float)
self.wt_filter = nn.Parameter(self.wt_filter, requires_grad=False)
self.iwt_filter = nn.Parameter(self.iwt_filter, requires_grad=False)
self.wt_function = partial(wavelet_transform, filters=self.wt_filter)
self.iwt_function = partial(inverse_wavelet_transform, filters=self.iwt_filter)

wt_type='db1' 默认就是 Haar 小波

requires_grad=False：滤波器固定（这点很重要：它是真"小波滤波器组"，不是可学习的卷积核）

(B) 子带域的可学习卷积（在 WT 后的空间上卷）

self.wavelet_convs = nn.ModuleList([
    nn.Conv2d(in_channels * 4, in_channels * 4, kernel_size,
              padding='same', groups=in_channels * 4, bias=bias)
    for _ in range(self.wt_levels)
])
self.wavelet_scale = nn.ModuleList([
    _ScaleModule([1, in_channels * 4, 1, 1], init_scale=0.1)
    for _ in range(self.wt_levels)
])

这里的核心是：

• 输入输出通道都是 4*C（因为 LL/LH/HL/HH 四个子带摊平到通道维）
• groups = 4*C：子带/通道完全不混合的 depthwise 卷积（极轻量）
• init_scale=0.1：一开始让小波分支"影响小一点"，训练更稳

© Mamba/SSM 全局分支

self.global_atten = SS2D(
    d_model=in_channels,
    d_state=int(ssm_ratio * in_channels),
    ssm_ratio=ssm_ratio,
    forward_type=forward_type,
    channel_first=True,
)
self.base_scale = _ScaleModule([1, in_channels, 1, 1])

SS2D 就是视觉版 Mamba / SSM 的 2D 扫描实现

base_scale 和小波分支一样：起到门控/缩放作用

本文不拆解完整代码，专注其中的小波分析部分，因此不在继续展开

单独看小波部分

1.MobileMamba 小波分支在做什么

给定输入特征 x∈RB×C×H×Wx ∈ R^{B×C×H×W}x∈RB×C×H×W：

1. DWT / WT（小波分解）

   用固定小波滤波器做 depthwise conv2d(stride=2)，得到 4 个子带：
   y∈RB×C×4×H/2×W/2y ∈ R^{B×C×4×H/2×W/2}y∈RB×C×4×H/2×W/2，其中 4 对应 LL, LH, HL, HH

2. 子带域卷积增强（可学习）

   把子带维摊平到通道维：[B, 4C, H/2, W/2]

   再做 depthwise 卷积 （MobileMamba 用的是 groups=4C）

   这一步的意义是：

   • 在半分辨率 上卷积 → 更大 ERF（同样 kernel 覆盖原图更大范围）

   • 显式处理 LH/HL/HH 高频子带 → 强化边缘/纹理

3. IWT（重构）

   用固定重构滤波器做 depthwise conv_transpose2d(stride=2)

   回到 xw∈RB×C×H×Wx_w ∈ R^{B×C×H×W}xw∈RB×C×H×W

4. （MobileMamba 中）最后是 x_out = x_mamba + x_w

2.即插即用模块

这里我把其中的小波部分抽取改造一下，构建成一个可以即插即用的模块，方便嫁接到其他模型中。我这里对每一行都加上了详细的注释，假设模块命名为WaveletEnhance2D:

import torch                          
import torch.nn as nn                 
import torch.nn.functional as F       
from functools import partial   
# PyWavelets：提供小波滤波器系数（Haar/db 等）
# pip install PyWavelets
import pywt                           


def _create_wavelet_filters(wt_type: str, channels: int, dtype=torch.float32):
    """
    生成固定的小波滤波器（用于 DWT/IDWT），并扩展成 depthwise 形式。
    输入：
      wt_type: 小波类型，如 "db1"（即 Haar）、"db2"...
      channels: 输入通道数 C
      dtype: 张量数据类型（默认 float32）
    输出：
      dec_filters: [4*C, 1, k, k]  # DWT 分解滤波器（LL/LH/HL/HH）
      rec_filters: [4*C, 1, k, k]  # IDWT 重构滤波器（对应四个子带）
    """
    #w长度为 4 的元组，按顺序存放了：
    #（分解低通，分解高通，重构低通，重构高通）这四个 1D 滤波器
    # (dec_lo, dec_hi, rec_lo, rec_hi)
    #[ 0.7071067811865476,  0.7071067811865476],
    #[-0.7071067811865476,  0.7071067811865476],
    #[ 0.7071067811865476,  0.7071067811865476],
    #[ 0.7071067811865476, -0.7071067811865476]
   
    w = pywt.Wavelet(wt_type)        # 从 pywt 中取出该小波的滤波器系数（1D）

    # ===== 1) 分解（DWT）用的 1D 滤波器 =====
    # 深度学习中的卷积（conv）和信号处理中"滤波"的定义方向是反的。
    # pywt 给的系数顺序与 conv2d 的权重排列方式不同，通常要 reverse 一下以对齐卷积定义
    dec_hi = torch.tensor(w.dec_hi[::-1], dtype=dtype)  # 高通（检测变化）
    dec_lo = torch.tensor(w.dec_lo[::-1], dtype=dtype)  # 低通（做平滑/平均）

    # ===== 2) 用外积把 1D 变成 2D 可分离滤波器（四个子带）=====
    # 外积 lo⊗lo, lo⊗hi, hi⊗lo, hi⊗hi 分别对应 LL/LH/HL/HH
    dec_2d = torch.stack([
        # 2D核=行方向滤波器⊗列方向滤波器 
        # 把两个 1D 滤波器变成「一行 × 一列」= 2x2
        # LL：低频×低频
        dec_lo.unsqueeze(0) * dec_lo.unsqueeze(1), 
        # LH：低频×高频（常用于"水平边缘"）
        dec_lo.unsqueeze(0) * dec_hi.unsqueeze(1),  
        # HL：高频×低频（常用于"垂直边缘"）
        dec_hi.unsqueeze(0) * dec_lo.unsqueeze(1),  
        # HH：高频×高频（角点/细纹理）
        dec_hi.unsqueeze(0) * dec_hi.unsqueeze(1),      
    ], dim=0)                                           # 形状：[4, k, k]

    # ===== 3) 扩展成 depthwise 的卷积核格式 =====
    # conv2d 需要 weight 形状为 [out_channels, in_channels/groups, k, k]
    # 这里我们希望"每个输入通道独立做小波分解"，所以用 groups=C（depthwise）。
    # 因而每个通道会输出 4 个子带 => 总输出通道 4*C，且每个输出通道只看 1 个输入通道 => in_channels/groups = 1
    #把"4个2D小波核（LL/LH/HL/HH）"复制到每个输入通道上，
    # 做成能用于groups=C的depthwise卷积权重。
    # dec_2d[:, None]=dec_2d.unsqueeze(1):[4, k, k]->[4, 1, k, k]
    # 因为：conv2d权重：[out_channels,in_channels/groups,k,k]
    # 希望做 depthwise（groups=C），所以每个输出通道只看 1 个输入通道
    # in_channels/groups = 1
    # [4, 1, k, k]只有一套核（只针对一个通道）
    # repeat(channels, 1, 1, 1) 会把 第 0 维复制 channels份->[4*channels, 1, k, k]
    # 也就是说：对每个通道都用同样的4个核（LL/LH/HL/HH）来一遍
    dec_filters = dec_2d[:, None].repeat(channels, 1, 1, 1)  # [4*C, 1, k, k]

    # ===== 4) 重构（IDWT）用的 1D 滤波器 =====
    # 注意：重构滤波器 rec_lo/rec_hi 与分解滤波器 dec_lo/dec_hi 不一定完全相同（取决于小波类型）
    # 这里按 MobileMamba 的实现方式做 flip/reverse 来对齐 transposed conv 的定义
    rec_hi = torch.tensor(w.rec_hi[::-1], dtype=dtype).flip(0)  # 重构高通
    rec_lo = torch.tensor(w.rec_lo[::-1], dtype=dtype).flip(0)  # 重构低通

    # 同样外积得到 2D 重构核：LL/LH/HL/HH
    rec_2d = torch.stack([
        rec_lo.unsqueeze(0) * rec_lo.unsqueeze(1),      # LL
        rec_lo.unsqueeze(0) * rec_hi.unsqueeze(1),      # LH
        rec_hi.unsqueeze(0) * rec_lo.unsqueeze(1),      # HL
        rec_hi.unsqueeze(0) * rec_hi.unsqueeze(1),      # HH
    ], dim=0)

    # 扩展成 [4*C, 1, k, k]，用于 conv_transpose2d + groups=C（depthwise 重构）
    rec_filters = rec_2d[:, None].repeat(channels, 1, 1, 1)

    return dec_filters, rec_filters                       # 返回分解/重构滤波器


def _dwt2(x, dec_filters):
    """
    2D 离散小波变换（DWT），用 conv2d 实现。
    输入：
      x: [B, C, H, W]
      dec_filters: [4*C, 1, k, k]
    输出：
      y: [B, C, 4, H/2, W/2]   # 4 对应 LL/LH/HL/HH
    """
    b, c, h, w = x.shape    # 取 batch、通道、高、宽
    # padding 的取法沿用 MobileMamba：让 stride=2 的卷积在尺寸上"对齐"小波分解
    # 这里 padding 是一个经验写法（不同实现可能略有差异）
    pad = (dec_filters.shape[2] // 2 - 1, dec_filters.shape[3] // 2 - 1)

    # depthwise 卷积：groups=c 表示每个输入通道独立卷积
    # stride=2 表示下采样（尺度减半），这是 DWT 的关键步骤之一
    # [B, 4C, H/2, W/2]
    y = F.conv2d(x, dec_filters, stride=2, groups=c, padding=pad)  

    # 把 4C 拆成 (C, 4)：每个通道都有 4 个子带
    # [B, C, 4, H/2, W/2]
    return y.reshape(b, c, 4, h // 2, w // 2)                     


def _idwt2(y, rec_filters):
    """
    2D 逆小波变换（IDWT），用 conv_transpose2d 实现。
    输入：
      y: [B, C, 4, H/2, W/2]
      rec_filters: [4*C, 1, k, k]
    输出：
      x: [B, C, H, W]
    """
    b, c, _, hh, ww = y.shape    # hh, ww 是半分辨率
    pad = (rec_filters.shape[2] // 2 - 1, rec_filters.shape[3] // 2 - 1)

    # 先把子带维度 4 摊平到通道：C*4
    y = y.reshape(b, 4 * c, hh, ww)   # [B, 4C, H/2, W/2]

    # depthwise 反卷积：groups=c 表示每个原始通道独立重构（同样不混通道）
    # stride=2 表示上采样回原分辨率
    # [B, C, H, W]
    x = F.conv_transpose2d(y, rec_filters, stride=2, groups=c, padding=pad)  
    return x


class WaveletEnhance2D(nn.Module):
    """
    即插即用的小波增强模块（提取自 MobileMamba 的 wavelet 分支思想）：

      x -> WT(固定) -> 子带域卷积(可学习) -> IWT(固定) -> x_w

    可选返回方式：
      - return_mode="wavelet": 输出仅为小波增强结果 x_w
      - return_mode="residual": 输出 x + alpha * x_w（更方便当残差块插进其他模型）

    子带域卷积的两种风格：
      - subband_conv="depthwise": groups=4C（MobileMamba 风格，极轻量，不混子带）
      - subband_conv="mix": groups=1（允许子带互相混合，表达力更强但更重）
    """
    def __init__(
        self,
        channels: int,                 # 输入/输出通道 C
        wt_type: str = "db1",          # 小波类型：db1=Haar
        kernel_size: int = 5,          # 子带域卷积核大小（MobileMamba 常用 5）
        wt_levels: int = 1,            # 小波分解层数（一般 1 就够轻量）
        subband_conv: str = "depthwise",
        return_mode: str = "residual",
        init_alpha: float = 0.1,       # 残差缩放初值（让模块一开始影响较小，训练更稳）
        bias: bool = False,            # 子带卷积是否使用 bias（通常可关）
    ):
        super().__init__()             # 初始化 nn.Module
        assert wt_levels >= 1          # 至少 1 层
        assert subband_conv in ("depthwise", "mix")
        assert return_mode in ("wavelet", "residual")

        self.channels = channels       # 保存通道数
        self.wt_levels = wt_levels     # 保存层数
        self.return_mode = return_mode # 保存返回方式

        # 生成固定的小波分解/重构滤波器（注意 dtype 固定 float32）
        dec, rec = _create_wavelet_filters(wt_type, channels, dtype=torch.float32)

        # 把滤波器注册为buffer：
        # - 会跟随模型 .to(device) 自动迁移到 GPU/CPU
        # - 会被保存进state_dict（persistent=True）
        # - 不会被优化器更新（不像 nn.Parameter）
        self.register_buffer("dec_filters", dec, persistent=True)
        self.register_buffer("rec_filters", rec, persistent=True)

        # 把 filters 固定到 WT/IWT 函数里，调用时只需要传 x
        self.wt = partial(_dwt2, dec_filters=self.dec_filters)
        self.iwt = partial(_idwt2, rec_filters=self.rec_filters)

        # 构造每一层 WT 对应的子带域卷积
        convs = []
        for _ in range(wt_levels):
            in_ch = 4 * channels  # 子带摊平后通道数是 4C
            # depthwise vs mix
            groups = in_ch if subband_conv == "depthwise" else 1  
            convs.append(
                nn.Conv2d(
                    in_ch, in_ch,            # 输入输出都是 4C
                    kernel_size=kernel_size, # 卷积核
                    padding="same",          # 保持 H/2,W/2 不变
                    groups=groups,           # depthwise: groups=4C
                    bias=bias,
                )
            )
        # 注册为 ModuleList，保证可训练参数被收集
        self.subband_convs = nn.ModuleList(convs)    

        # alpha 是一个可学习标量（或者你也可以改成每通道缩放）
        # 在 residual 模式下输出：x + alpha * x_w
        self.alpha = nn.Parameter(torch.tensor(float(init_alpha)))

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        """
        输入：
          x: [B, C, H, W]
        输出：
          - wavelet 模式：x_w
          - residual 模式：x + alpha*x_w
        """
        b, c, h, w = x.shape
        assert c == self.channels, f"channels mismatch: got {c}, expected {self.channels}"

        # ===== 多层小波分解：只递归 LL，保留高频子带 =====
        ll_stack = []      # 存每层处理后的 LL
        h_stack = []       # 存每层处理后的 (LH, HL, HH)
        shape_stack = []   # 存每层分解前的原始形状（用于裁剪 pad）
        ll = x             # 当前要分解的低频输入（初始为 x）

        for i in range(self.wt_levels):
            # 记录该层输入形状（未 pad 前的目标裁剪尺寸）
            shape_stack.append(ll.shape)          

            # WT 要求 H/W 可被 2 整除，否则 stride=2 的下采样会出问题
            H, W = ll.shape[-2], ll.shape[-1]
            if (H % 2) or (W % 2):                 # 只要有一个是奇数就 pad
                ll = F.pad(ll, (0, W % 2, 0, H % 2))  # 右边/下边补 1 像素使其变偶数

            # 做 WT：得到 4 子带
            y = self.wt(ll)                        # [B, C, 4, H/2, W/2]
            ll = y[:, :, 0, :, :]                  # LL 子带作为下一层继续分解（多层时）

            # ===== 在子带空间做卷积增强 =====
            # 把 4 子带摊平到通道维，方便用普通 Conv2d 处理
            y_flat = y.reshape(b, 4 * c, y.shape[-2], y.shape[-1])  # [B, 4C, H/2, W/2]

            # 子带域卷积：depthwise 时每个"子带通道"独立卷积，非常轻量
            y_flat = self.subband_convs[i](y_flat)  # [B, 4C, H/2, W/2]

            # reshape 回 [B, C, 4, H/2, W/2]
            y = y_flat.reshape_as(y)

            # 将该层处理后的 LL 和高频子带保存起来，供后面 IWT 逐层重构
            ll_stack.append(y[:, :, 0, :, :])       # 存 LL
            h_stack.append(y[:, :, 1:4, :, :])      # 存 (LH, HL, HH)

        # ===== 逐层逆变换重构：从最深层往回合成 =====
        next_ll = 0                                 # 用于多层情况下 LL 的"跨层残差累积"
        for i in range(self.wt_levels - 1, -1, -1): # 反向遍历
            ll_i = ll_stack.pop()                   # 取出该层 LL
            h_i = h_stack.pop()                     # 取出该层高频子带
            orig_shape = shape_stack.pop()          # 取出该层原始尺寸（用于 crop）

            # 多层时，把更深层重构回来的结果加到当前层 LL 上（与 MobileMamba 一致）
            ll_i = ll_i + next_ll

            # 拼回 [B, C, 4, h/2, w/2]，准备 IWT
            y = torch.cat([ll_i.unsqueeze(2), h_i], dim=2)

            # IWT：上采样回该层的空间分辨率
            next_ll = self.iwt(y)                   # [B, C, h, w]

            # 如果之前 pad 过（奇数尺寸），裁剪回原始大小
            next_ll = next_ll[:, :, :orig_shape[-2], :orig_shape[-1]]

        x_w = next_ll                               # 小波分支的最终输出（增强后的重构特征）

        # ===== 输出方式 =====
        if self.return_mode == "wavelet":
            return x_w                               # 只输出小波结果
        return x + self.alpha * x_w                  # 残差输出（更适合即插即用）

测试：

if __name__ == "__main__":
    x = torch.randn(2, 64, 63, 65)  # 故意用奇数 H/W 测试 pad/crop
    blk = WaveletEnhance2D(
        channels=64,
        wt_type="db1",
        kernel_size=5,
        wt_levels=1,
        subband_conv="depthwise",
        return_mode="residual",
        init_alpha=0.1,
    )

    y = blk(x)
    print("x:", x.shape, "y:", y.shape)  # y should be same as x

几点值得注意的：

**在 WT（小波变换）和 IWT（逆小波变换）中：**MobileMamba 中的小波不是"卷积特征提取"，

而是一个固定、逐通道的频率/尺度分解算子， 学习发生在小波分解之后的子带空间。

疑问1：为什么不用可学习卷积核？

因为 WT 的目的不是"提特征"，而是：

• 结构性分解

• 频率/尺度分离

• 保证可逆性（IWT 能还原）

疑问2：如果卷积核可学习：小波的"低频 / 高频"语义会被破坏，DWT + IWT 不再是严格可逆，行为退化成普通 stride=2 卷积 + 反卷积。

MobileMamba 刻意不让这部分学习，把学习能力放在后面的子带卷积和 Mamba 分支

"逐通道"这一点非常重要（不是可有可无） ，如果不用 groups=C，而是普通卷积：不同通道会混在一起，LL/LH/HL/HH 不再是"每个通道自己的子带"，小波分解失去明确物理意义。👉 逐通道是"这还是不是小波"的分水岭。

疑问3：哪些地方是"固定不学"，哪些地方是"学的"？

在 MobileMamba / WaveletEnhance2D 里，角色分工非常清晰：

模块	是否可学习	作用
WT (DWT)	❌ 固定	分解为 LL/LH/HL/HH
IWT	❌ 固定	重构回原分辨率
子带域卷积	✅ 学习	在低分辨率空间增强特征
α / scale	✅ 学习	控制小波分支强度
Mamba (SS2D)	✅ 学习	全局建模

上面的说明可能会有人困惑，既然说小波的核是固定的，为什么又说子带域卷积是可学习的？需要注意的是，完整小波分支其实是：

输入 x
 ├─① WT（固定，不学习）
 │     ↓
 │   子带表示 [LL, LH, HL, HH]
 │
 ├─② 子带域卷积（可学习）
 │     ↓
 │   增强后的子带特征
 │
 └─③ IWT（固定，不学习）
       ↓
     输出 x_w

疑问4：WT / IWT 在做什么？WT：把原空间特征 → 低频 + 不同方向的高频，是一个结构性、可解释的变换 。IWT：把这些子带 → 合成回原空间，要求严格可逆。这一步的目标不是"学任务"，而是明确地告诉网络哪些是轮廓？哪些是边缘？哪些是纹理？所以它必须固定，否则低频/高频语义会漂移，DWT + IWT 不再可逆，小波就退化成"普通 stride=2 卷积"。类比一句话：WT 就像是把图像从 RGB 转成 YUV ------你不希望这个颜色空间转换是"学出来的"。

疑问5：**那为什么"子带域卷积"又是可学习的？（网络层）**子带域卷积在做什么？它并不是在"定义小波"，而是在利用小波分解后的表示。它回答的问题是：在已经明确知道"这是低频 / 这是水平边缘 / 这是垂直边缘 / 这是角点" 的前提下，哪些模式对当前任务更重要？如何组合它们？这正是深度学习该干的事。

从上面的代码角度看，它们是两类完全不同的"卷积"：

模块	用的卷积	是否学习	本质
WT	conv2d(groups=C)	❌	实现小波算子
子带域卷积	Conv2d(groups=4C or 1)	✅	特征增强层
IWT	conv_transpose2d(groups=C)	❌	逆小波算子

👉 虽然都叫卷积 ，但角色完全不同。

小波变换（WT/IWT）本身是一个固定、逐通道的频率分解算子；

网络的学习发生在小波分解之后的子带特征空间中，用可学习的卷积对各子带进行增强与建模。

疑问6：为什么要引入 alpha，而且还要有 init_alpha？

小波分支虽然是"结构合理的"，但在训练一开始，主干网络（CNN / Mamba / Transformer）已经是一个成熟、稳定的表示路径。而小波分支，经过 WT / IWT（非标准 CNN 操作），子带卷积随机初始化，输出分布一开始不可控。因此，训练一开始，小波分支 ≈ 一个"轻微的扰动/微调项"，而不是主导特征。随着训练进行，如果小波分支有用，梯度会推动 alpha 变大，网络自己决定"要不要用小波、用多少"。init_alpha 不是"让小波更强"，而是"让小波先学会谦虚，再慢慢证明自己"。

论文外探讨

以下探讨仅作为个人观点，不是mobilemamba论文或者代码内容，如有错误请指出！

一些疑问

问题1：如果让子带卷积"部分共享权重"会怎样？

个人觉得，部分共享"是一个非常有前途的折中方案，在不破坏小波语义的前提下，提高跨方向一致性与参数效率。但前提是：**共享的方式要"结构化"，不能随便混。**前设计（groups=4C）意味着不混合，这样语义最纯，方向性最清晰，但是参数利用率低，同方向的"边缘模式"无法协同。

问题2：如果只让 LL 可学习，高频固定，会不会更稳？

在很多任务中， 只学 LL，高频固定"会更稳，尤其在小模型、少数据、噪声多的场景下。因为高频子带的特点是对噪声极其敏感，梯度波动大，任务相关性不稳定（分类 vs 分割差异大）。如果可学习，网络可能过拟合"假边缘"或或在早期训练中扰乱主干特征。

问题3：如果把 WT 当成一个"不可学习的 tokenizer"，再接 Transformer/Mamba，会发生什么？

WT 作为 tokenizer + Transformer/Mamba是一个非常"干净、合理、低噪声"的结构设计，尤其适合：轻量模型、长序列建模、结构敏感任务。

一个好的 tokenizer 应该：

要求	WT 是否满足
降维	✅ stride=2
结构保留	✅ 低频/高频显式
可解释	✅ 频率/方向
不引入噪声	✅ 固定算子

一些使用小波的方案

WT 比「patchify + linear」结构性强得多。所以现有文献中有三种接法：

🔹 方案 A：只用 LL 当 token（最稳）

用固定的小波变换（WT）把输入特征做一次"结构化下采样"， 只保留低频子带 LL 作为"语义 token"， 再把这些 token 当作序列送进 Transformer 或 Mamba 做全局建模。用 WT 代替 patch embedding / stride conv，作为一种"更有结构的 tokenizer"。

x → WT → LL → flatten → Transformer / Mamba
张量变化：
x:        [B, C, H, W]
WT(x):    [B, C, 4, H/2, W/2]
LL:      [B, C, H/2, W/2]
flatten: [B, C, (H/2)*(W/2)]# 等价于ViTpatchify + linear embedding
permute: [B, (H/2)*(W/2), C]#  WT-based semantic tokenization

当然这样自然引入一个疑问，只要LL，会不会造成信息丢失太多？这里需要注意的是**深度学习里的很多任务，本来就不需要"完整信息"。**如常规图像分类 / 场景识别 / 粗粒度判断或全局建模为主（Transformer / Mamba），用 LL 当 token，反而"更符合模型假设"。而对于需要精细定位的任务，如语义分割（尤其边界）、关键点检测、超分辨率、医学 / 工业缺陷检测等高频 = 关键信息，"细节本身就是类别线索"的场景，丢失高频问题会很大。

🔹 方案 B：四个子带分别建模（研究级）

LL tokens
LH tokens
HL tokens
HH tokens

后面接多流 Transformer，表达力强，但复杂

🔹 方案 C：LL 主干 + 高频作为 bias / prompt

LL → main tokens
LH/HL/HH → condition / modulation

有点类似条件注意力

所以感觉小波变换对 Mamba 特别友好，因为

• Mamba 擅长：长序列、连续结构
• WT 后：token 数显著减少、序列更"平滑"、高频不直接扰动状态转移

👉 WT + Mamba 是"结构上天然互补"的组合

下面我把之前给出的WaveletEnhance2D进行稍微改造，得到三个方案的版本。

三种方案的实现

在MobileMamba的小波块（以我抽取出来的即插即用WaveletEnhance2D为基础）改进得到三种方案，这里先陈述一下：

WaveletEnhance2D 原来做的是：

WT（固定）→ 子带卷积（可学）→ IWT（固定）→ 回到 2D

而你现在的"tokenizer"路线需要的是：

WT（固定）→ 选子带（LL 或全部）→ 映射到 token 维度（可学）→ flatten 成序列

所以我们把重点放在 WT 之后怎么变 token，不再一定要 IWT。

1. 变体 A：只用 LL 当 token

import torch
import torch.nn as nn
import torch.nn.functional as F
from functools import partial

# 复用之前写的：
# _create_wavelet_filters, _dwt2

class WaveletLLTokenizer(nn.Module):
    """
    x -> WT -> LL -> (proj) -> flatten -> tokens
    输出 tokens: [B, N, d_model]
    """
    def __init__(self, in_channels, wt_type="db1", d_model=None, add_norm=False):
        super().__init__()
        self.in_channels = in_channels
        self.d_model = d_model or in_channels

        dec, _ = _create_wavelet_filters(wt_type, in_channels, dtype=torch.float32)
        self.register_buffer("dec_filters", dec, persistent=True)
        self.wt = partial(_dwt2, dec_filters=self.dec_filters)

        # 把 LL 的通道投影到 d_model（可选但很实用）
        self.proj = nn.Identity() if self.d_model == in_channels else nn.Conv2d(in_channels, self.d_model, 1)
        self.norm = nn.LayerNorm(self.d_model) if add_norm else nn.Identity()

    def forward(self, x):
        b, c, h, w = x.shape
        assert c == self.in_channels
        if (h % 2) or (w % 2):
            x = F.pad(x, (0, w % 2, 0, h % 2))

        y = self.wt(x)                # [B,C,4,H/2,W/2]
        ll = y[:, :, 0, :, :]         # [B,C,H/2,W/2]
        ll = self.proj(ll)            # [B,d_model,H/2,W/2]

        tokens = ll.flatten(2).transpose(1, 2)  # [B,N,d_model]
        tokens = self.norm(tokens)
        return tokens

接 Transformer/Mamba

tokens = tokenizer(x)        # [B,N,d_model]
out = backbone(tokens)       # Transformer/Mamba block

2. 变体 B：LL 主干 token + 高频作为 modulation/prompt

同样取 LL 做主 token：tllt_{ll}tll

高频 LH/HL/HH 聚合成一个"条件向量" cond，例如：

• 先把三块拼到通道：hf=[B,3C,H/2,W/2]
• 再全局池化：[B,3C]
• 再 MLP → 得到 γ，β\gamma，\betaγ，β（FiLM 风格调制）

用 t=tll∗(1+γ)+βt = t_{ll} * (1+\gamma) + \betat=tll∗(1+γ)+β 去调制 token（或把 cond 作为 prompt token 拼到序列开头）

class WaveletLLWithHFModTokenizer(nn.Module):
    """
    x -> WT -> LL tokens
         WT -> HF summary -> gamma/beta -> modulate LL tokens
    输出 tokens: [B,N,d_model]
    """
    def __init__(self, in_channels, wt_type="db1", d_model=None, hidden=256, add_norm=False):
        super().__init__()
        self.in_channels = in_channels
        self.d_model = d_model or in_channels

        dec, _ = _create_wavelet_filters(wt_type, in_channels, dtype=torch.float32)
        self.register_buffer("dec_filters", dec, persistent=True)
        self.wt = partial(_dwt2, dec_filters=self.dec_filters)

        self.proj = nn.Identity() if self.d_model == in_channels else nn.Conv2d(in_channels, self.d_model, 1)

        # 高频条件分支：3C -> 2*d_model（输出 gamma,beta）
        self.cond_mlp = nn.Sequential(
            nn.Linear(3 * in_channels, hidden),
            nn.GELU(),
            nn.Linear(hidden, 2 * self.d_model),
        )

        self.norm = nn.LayerNorm(self.d_model) if add_norm else nn.Identity()

    def forward(self, x):
        b, c, h, w = x.shape
        assert c == self.in_channels
        if (h % 2) or (w % 2):
            x = F.pad(x, (0, w % 2, 0, h % 2))

        y = self.wt(x)                      # [B,C,4,H/2,W/2]
        ll = y[:, :, 0, :, :]               # [B,C,H/2,W/2]
        hf = y[:, :, 1:4, :, :]             # [B,C,3,H/2,W/2]
        hf = hf.reshape(b, 3 * c, hf.shape[-2], hf.shape[-1])  # [B,3C,H/2,W/2]

        # 高频条件向量：全局平均池化
        cond = hf.mean(dim=(2, 3))          # [B,3C]
        gamma_beta = self.cond_mlp(cond)    # [B,2*d_model]
        gamma, beta = gamma_beta.chunk(2, dim=-1)  # 各 [B,d_model]
        gamma = gamma.unsqueeze(1)          # [B,1,d_model]
        beta = beta.unsqueeze(1)            # [B,1,d_model]

        ll = self.proj(ll)                  # [B,d_model,H/2,W/2]
        tokens = ll.flatten(2).transpose(1, 2)  # [B,N,d_model]

        # FiLM 调制：用高频信息调制 LL token
        tokens = tokens * (1.0 + gamma) + beta
        tokens = self.norm(tokens)
        return tokens

这种方式，LL 提供稳定语义 token，高频不直接变 token（避免噪声），而是作为"条件"去调制 LL → 通常更稳。

3. 变体 C：多流 token（LL/LH/HL/HH 分开建模）

这个变体有两种常见落地方式：

C1：把 4 个子带都 flatten 成 token，并加 "子带类型嵌入"

• tokens 总长度是 4N

• 用一个 type embedding（0~3）告诉模型每个 token 来自哪个子带

• 最简单直接，适合 Transformer；Mamba 也能用，但序列更长

class WaveletMultiStreamTokenizer(nn.Module):
    """
    x -> WT -> [LL,LH,HL,HH] -> flatten each -> concat -> tokens
    tokens: [B, 4N, d_model]
    """
    def __init__(self, in_channels, wt_type="db1", d_model=None, add_type_emb=True, add_norm=False):
        super().__init__()
        self.in_channels = in_channels
        self.d_model = d_model or in_channels
        self.add_type_emb = add_type_emb

        dec, _ = _create_wavelet_filters(wt_type, in_channels, dtype=torch.float32)
        self.register_buffer("dec_filters", dec, persistent=True)
        self.wt = partial(_dwt2, dec_filters=self.dec_filters)

        # 可选：每个子带先过 1×1 conv 投影到 d_model（共享一套更省参数）
        self.proj = nn.Identity() if self.d_model == in_channels else nn.Conv2d(in_channels, self.d_model, 1)

        if add_type_emb:
            self.type_emb = nn.Embedding(4, self.d_model)  # 0:LL 1:LH 2:HL 3:HH
        else:
            self.type_emb = None

        self.norm = nn.LayerNorm(self.d_model) if add_norm else nn.Identity()

    def forward(self, x):
        b, c, h, w = x.shape
        assert c == self.in_channels
        if (h % 2) or (w % 2):
            x = F.pad(x, (0, w % 2, 0, h % 2))

        y = self.wt(x)  # [B,C,4,H/2,W/2]
        tokens_list = []
        for band in range(4):
            feat = y[:, :, band, :, :]          # [B,C,H/2,W/2]
            feat = self.proj(feat)              # [B,d_model,H/2,W/2]
            t = feat.flatten(2).transpose(1, 2) # [B,N,d_model]
            if self.type_emb is not None:
                t = t + self.type_emb(torch.tensor(band, device=x.device)).view(1,1,-1)
            tokens_list.append(t)

        tokens = torch.cat(tokens_list, dim=1)  # [B,4N,d_model]
        tokens = self.norm(tokens)
        return tokens

C2：四条流分别进四个 backbone，再融合（更像"多分支网络"）

• 更强但更重，代码也更长
• 常见融合：concat + 1×1、cross-attn、或加权求和

怎么把它接回 2D ？如果你最后还想回到 [B,C,H,W]（比如做分割），通常做法是：

• backbone 输出 tokens [B,N,d]
• reshape 回 [B,d,H/2,W/2]
• 再上采样（或者 IWT，用 LL + 高频重构）