基于Stacking集成学习的数据回归预测(4种基学习器PLS、SVM、决策、KNN,多种元学习器比选)MATLAB代码:
一、研究背景
- 集成学习是机器学习中提高预测精度和泛化能力的重要方法
- Stacking(堆叠) 是一种双层集成策略,通过组合多个基学习器的预测结果,再由元学习器进行最终预测
- 适用于解决复杂回归问题,特别是在单一模型性能有限时
二、主要功能
- 数据预处理:读取Excel数据、标准化处理、数据集划分
- 多模型训练:训练4种基学习器(PLS、SVM、决策树、KNN)
- Stacking集成:构建元特征、训练元学习器
- 模型评估:多维度性能比较、提升分析
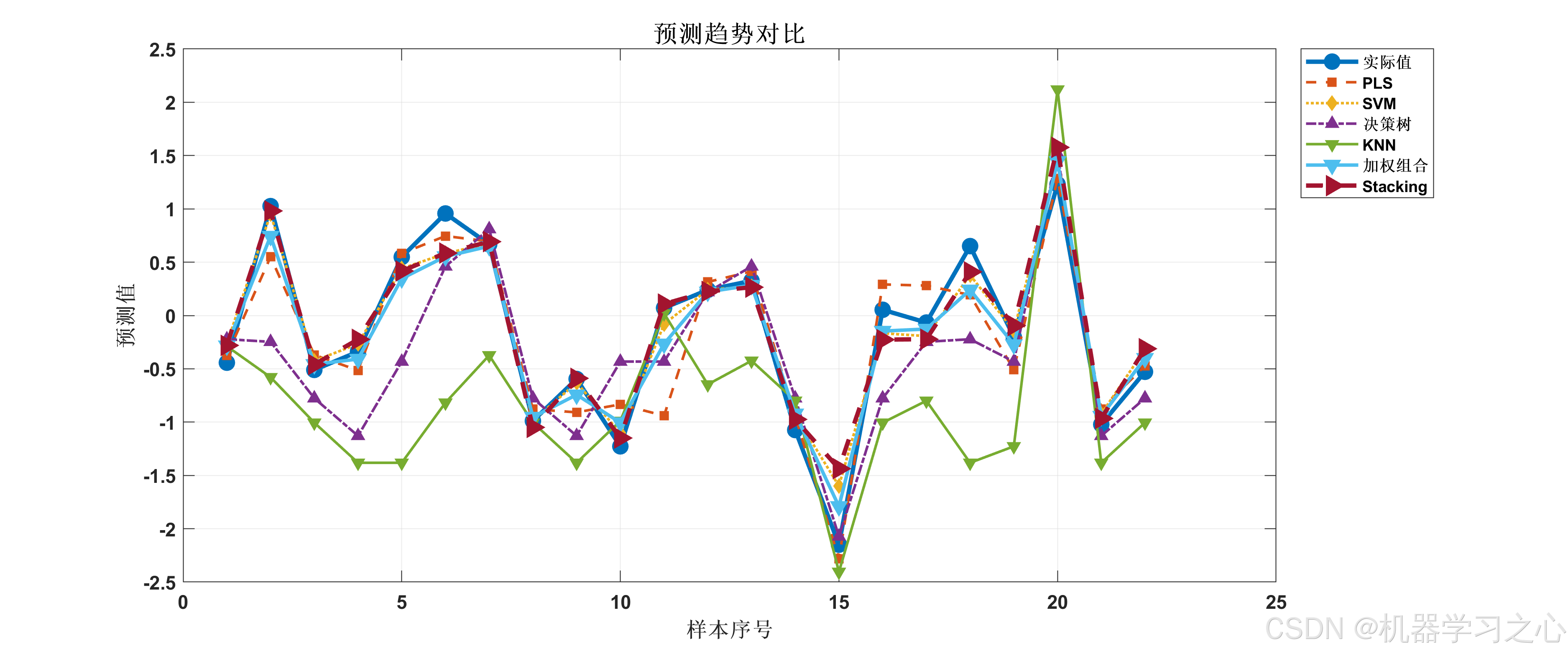
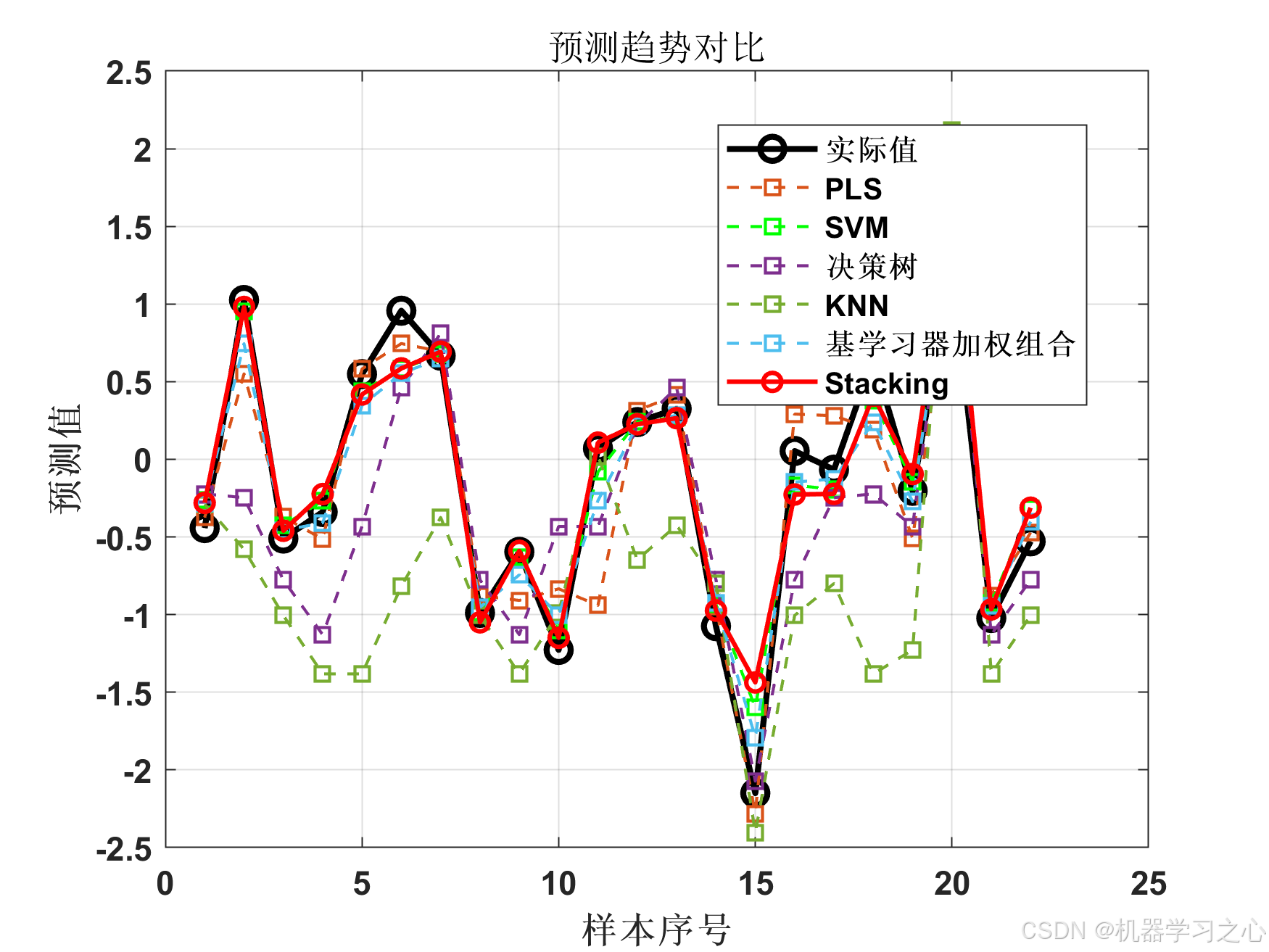
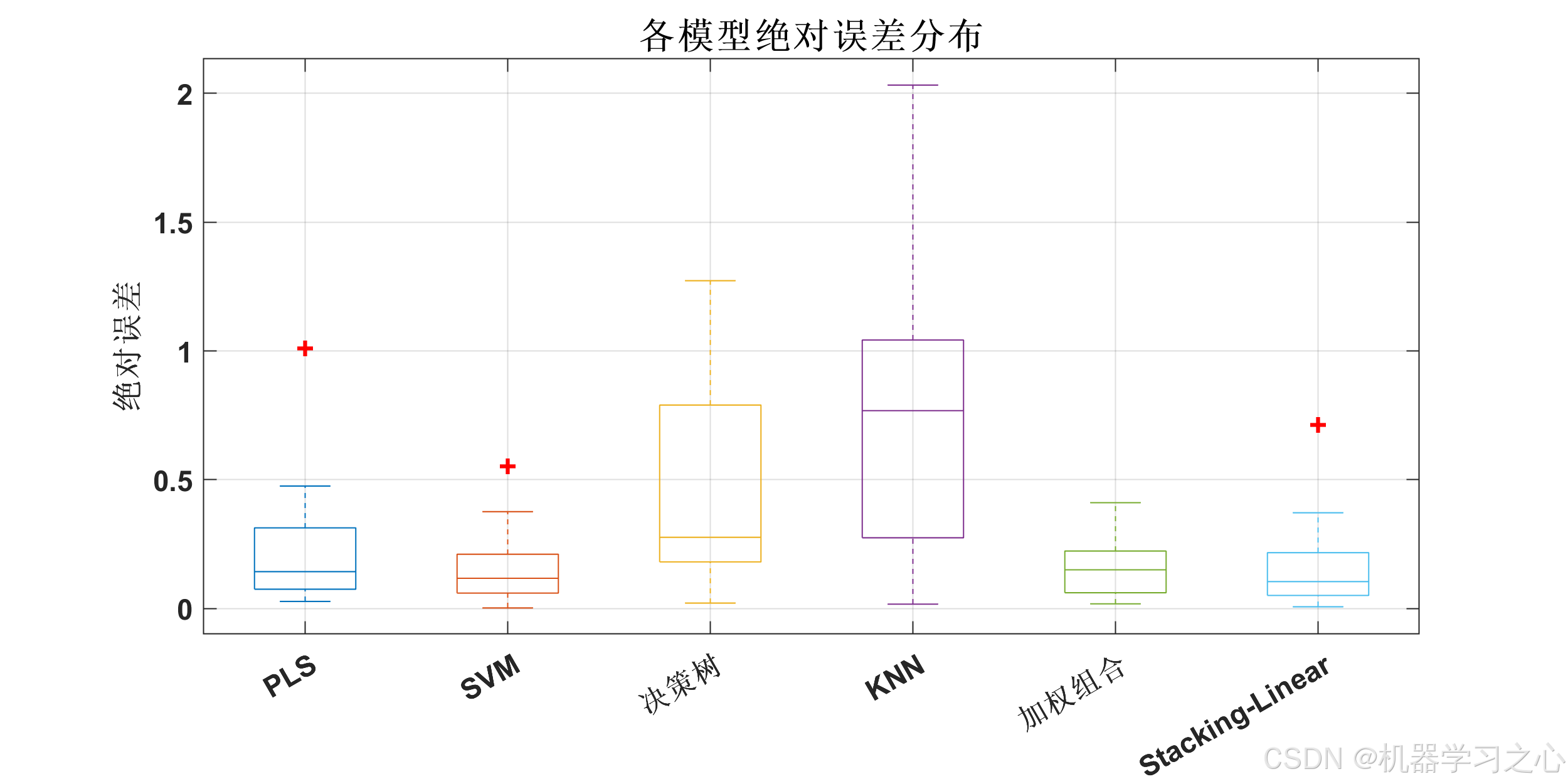
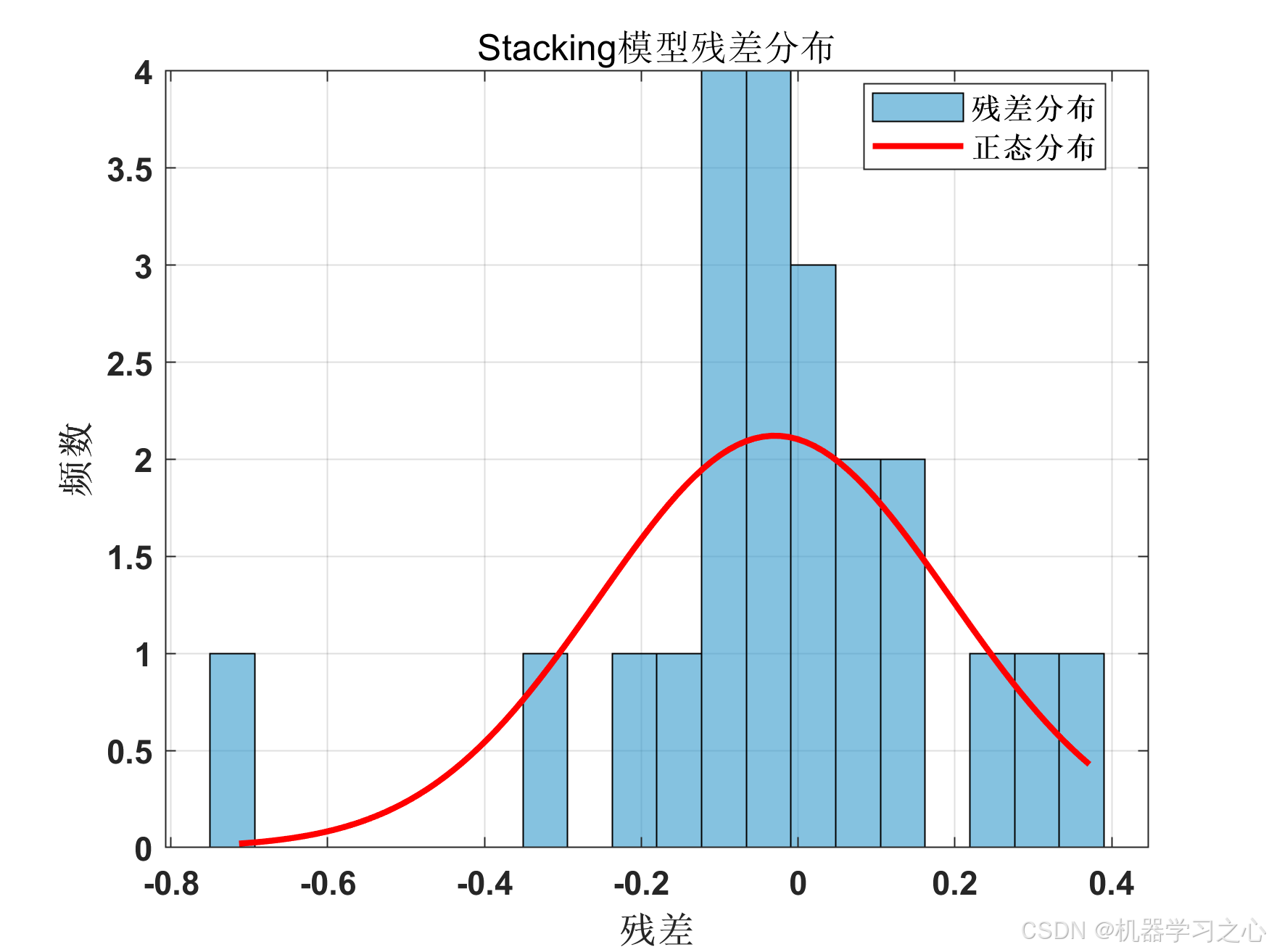
- 可视化分析:多种图形展示预测效果
- 模型保存:保存最佳集成模型
三、算法步骤
- 数据准备 → 标准化 → 划分训练/验证/测试集(60%/20%/20%)
- 基学习器训练 :
- PLS:交叉验证选择最佳成分数
- SVM:网格搜索优化参数
- 决策树和KNN:增加模型多样性
- 元特征构建 :
- 基学习器预测值
- 交互特征(预测值乘积)
- 统计特征(标准差、极差)
- 元学习器选择 :
- 候选:随机森林、梯度提升、线性回归、岭回归
- 基于验证集MSE选择最佳
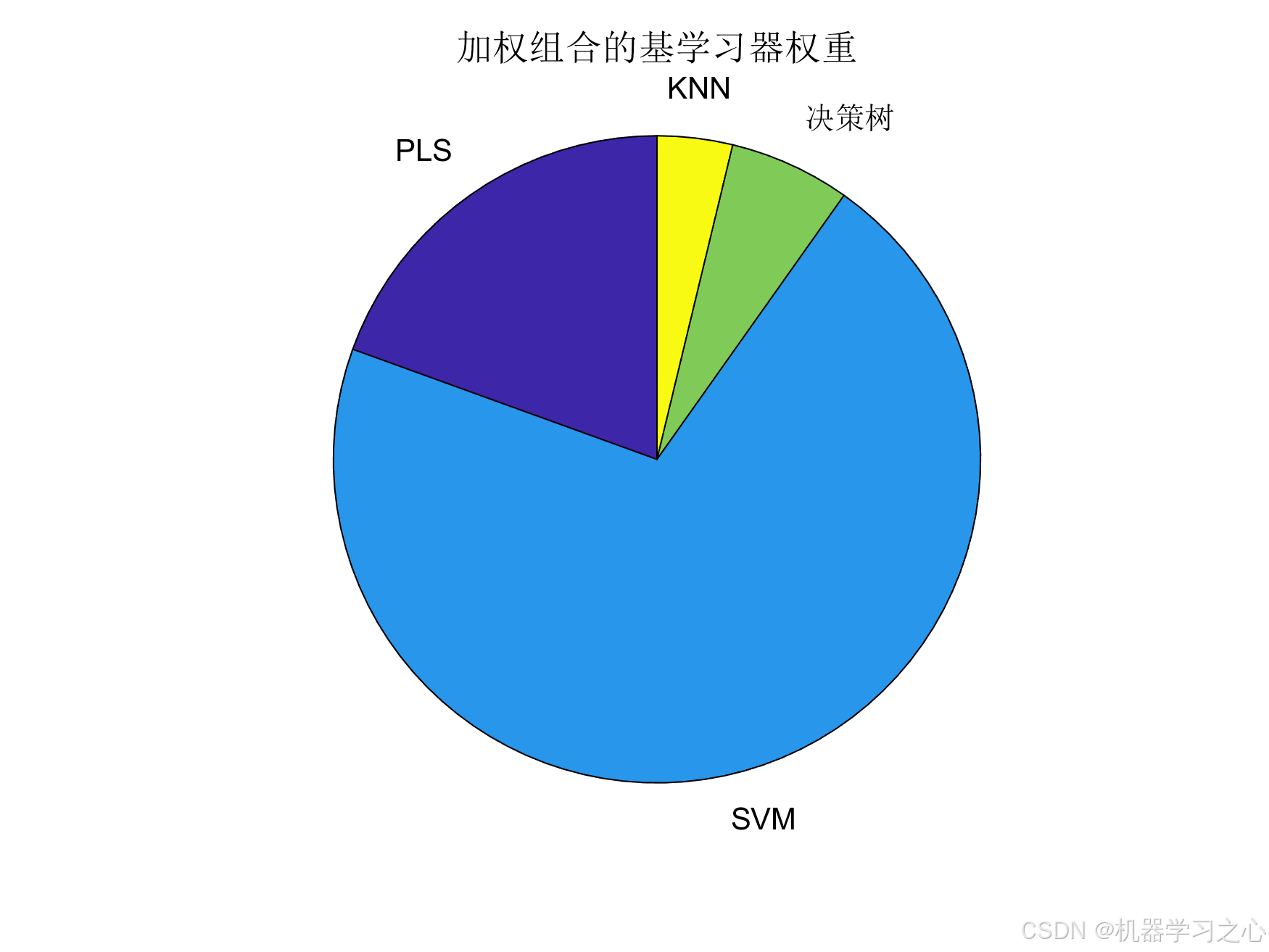
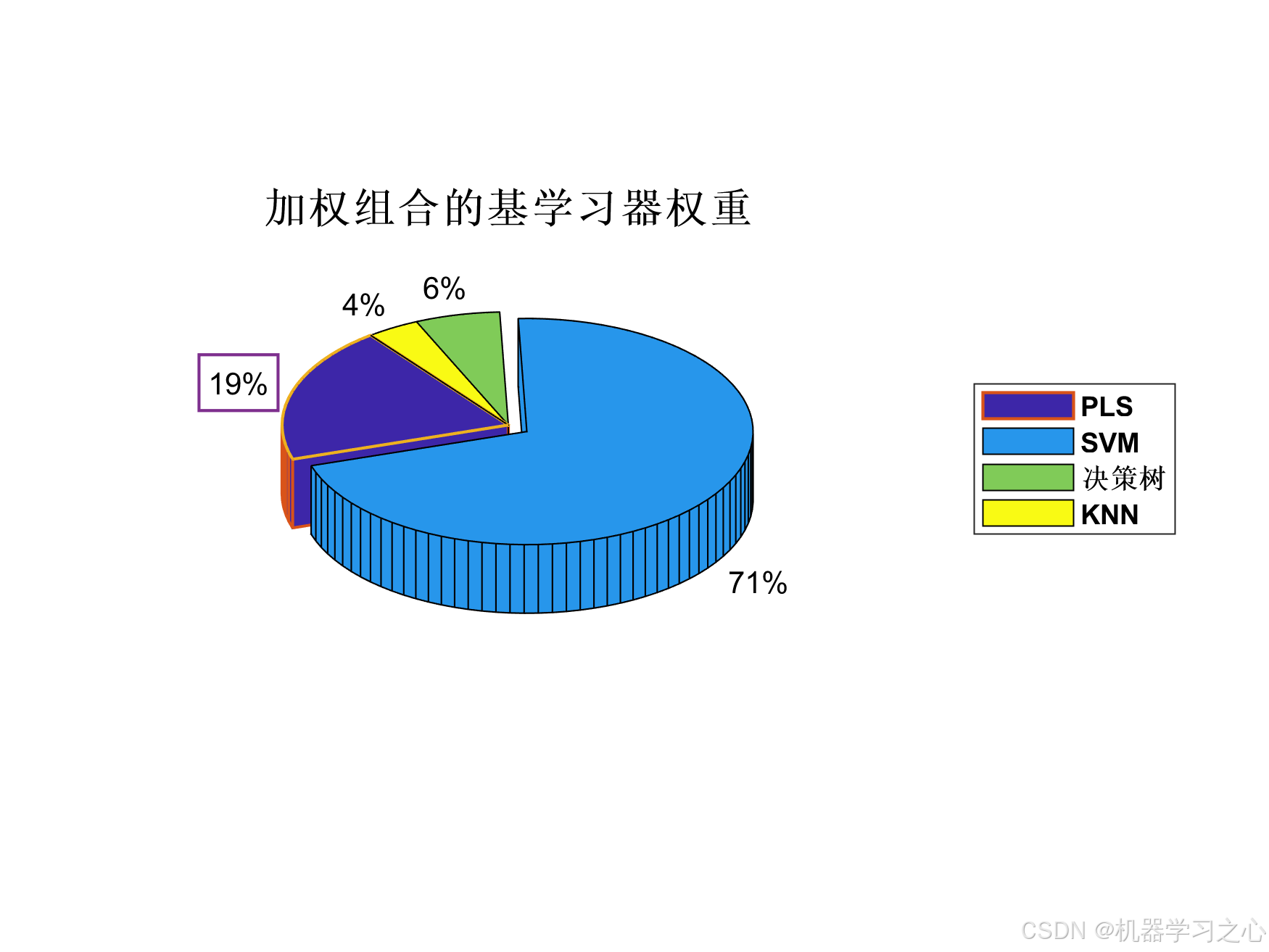
- 加权组合策略:基于性能的权重分配
- 性能评估与可视化
四、技术路线
原始数据 → 标准化 → 基学习器训练 → 元特征构建 → 元学习器训练 → 集成预测
↓ ↓ ↓ ↓ ↓ ↓
数据预处理 PLS/SVM/ 预测结果 特征工程 模型选择 最终输出
决策树/KNN 交互/统计 (RF/GB/线性)五、公式原理
1. Stacking核心思想:
y^stacking=fmeta(h1(x),h2(x),...,hT(x)) \hat{y}{\text{stacking}} = f{\text{meta}}(h_1(x), h_2(x), ..., h_T(x)) y^stacking=fmeta(h1(x),h2(x),...,hT(x))
其中 hih_ihi是基学习器,fmetaf_{\text{meta}}fmeta是元学习器
2. 加权组合权重:
wi=1MSEi+ϵ/∑j=1T1MSEj+ϵ w_i = \frac{1}{MSE_i + \epsilon} / \sum_{j=1}^{T} \frac{1}{MSE_j + \epsilon} wi=MSEi+ϵ1/j=1∑TMSEj+ϵ1
3. 性能指标:
- MSE:均方误差
- R²:决定系数
- MAE:平均绝对误差
- MAPE:平均绝对百分比误差
六、参数设定
基学习器参数:
- PLS:成分数1-15,5折交叉验证
- SVM:C=[0.01,0.1,1,10,100,1000],gamma=[0.001,0.01,0.1,1,10]
- 决策树:MinParentSize=10,MaxNumSplits=100
- KNN:NumNeighbors=5,距离度量=欧式
元学习器参数:
- 随机森林:100棵树,MinLeafSize=10
- 梯度提升:100轮,学习率0.1
- 岭回归:Lambda=0.1
七、运行环境
- 软件:MATLAB(需要Statistics and Machine Learning Toolbox)
- 数据格式:Excel文件(最后一列为目标变量)
- 建议配置:MATLAB R2020b或更高版本
八、应用场景
- 金融预测:股票价格、汇率预测
- 工业预测:设备故障预测、产量预测
- 医疗预测:疾病风险预测、治疗效果评估
- 商业预测:销售额预测、客户流失预测
- 科学研究:实验数据建模、参数优化
九、创新点
- 元特征工程:添加交互特征和统计特征
- 多样性增强:使用不同类型的基学习器
- 双策略对比:同时实现Stacking和加权组合
- 全面评估:包含相关性分析和多样性评估
- 可视化丰富:多种图形展示预测效果
十、注意事项
- 需要根据实际数据调整基学习器参数
- 基学习器相关性过高会降低Stacking效果
- 数据标准化对SVM和PLS等模型很重要
- 验证集用于模型选择,避免过拟合
matlab
=== 数据准备和预处理 ===
数据集划分: 训练集: 61, 验证集: 20, 测试集: 22
=== 训练基学习器(增加多样性) ===
1. 训练PLS模型...
PLS最佳成分数: 3
PLS验证集MSE: 0.110131
2. 训练SVM模型(改进网格搜索)...
SVM最佳参数: C=10.00, gamma=0.100
SVM验证集MSE: 0.030325
3. 训练决策树模型(增加多样性)...
决策树验证集MSE: 0.354698
4. 训练KNN模型(增加多样性)...
KNN验证集MSE: 0.569963
=== 创建元特征(关键优化) ===
添加交互特征...
添加统计特征...
元特征维度: 61 × 9
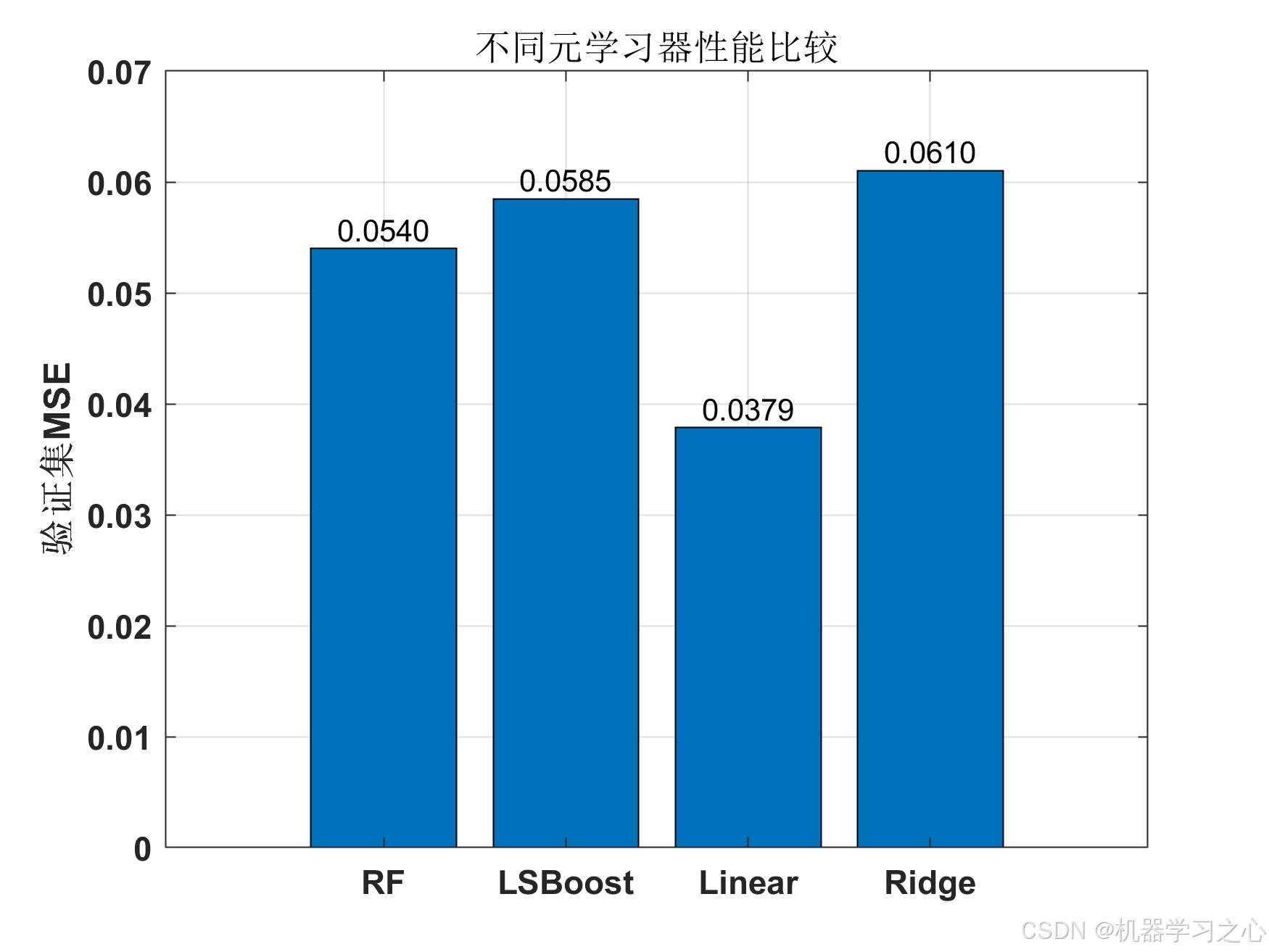
=== 训练和选择元学习器 ===
尝试元学习器: RF...
RF验证集MSE: 0.054018
尝试元学习器: LSBoost...
LSBoost验证集MSE: 0.058475
尝试元学习器: Linear...
Linear验证集MSE: 0.037861
尝试元学习器: Ridge...
Ridge验证集MSE: 0.061026
最佳元学习器: Linear (MSE: 0.037861)
=== 尝试加权组合策略 ===
加权组合验证集MSE: 0.043765
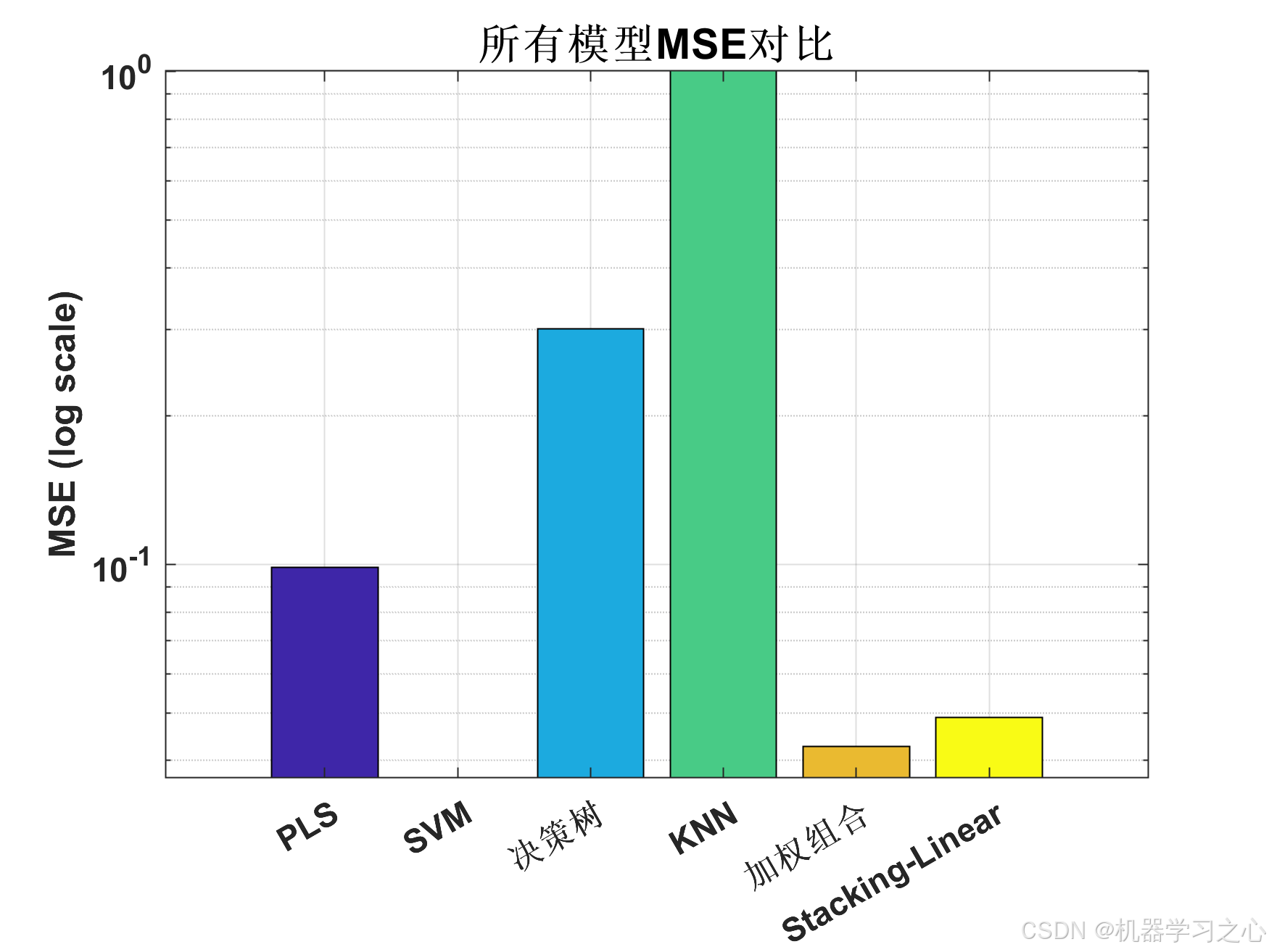
========== 性能评估 ==========
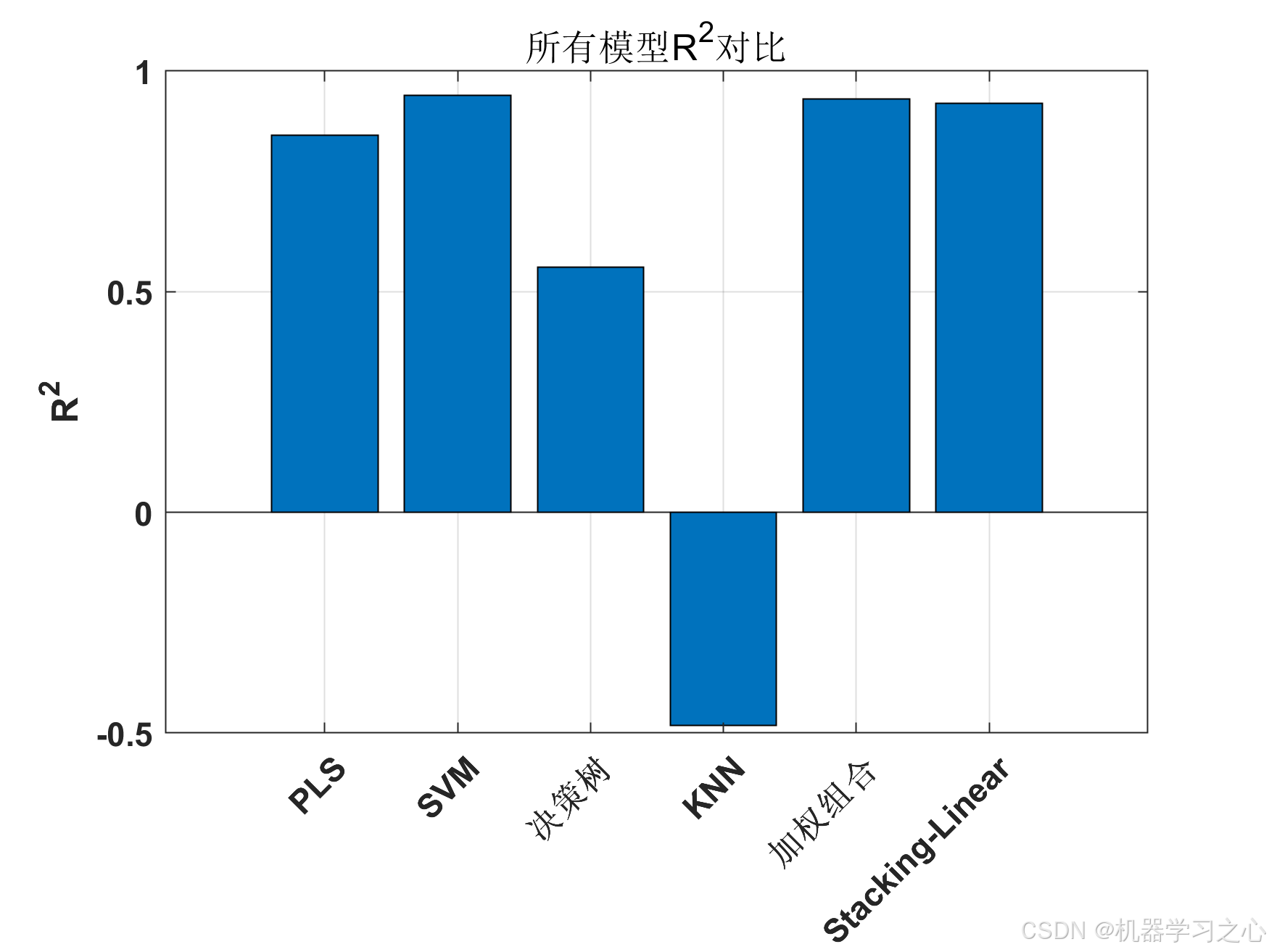
Model MSE RMSE MAE R2 R2_adj MAPE
___________________ ________ _______ _______ ________ _______ ______
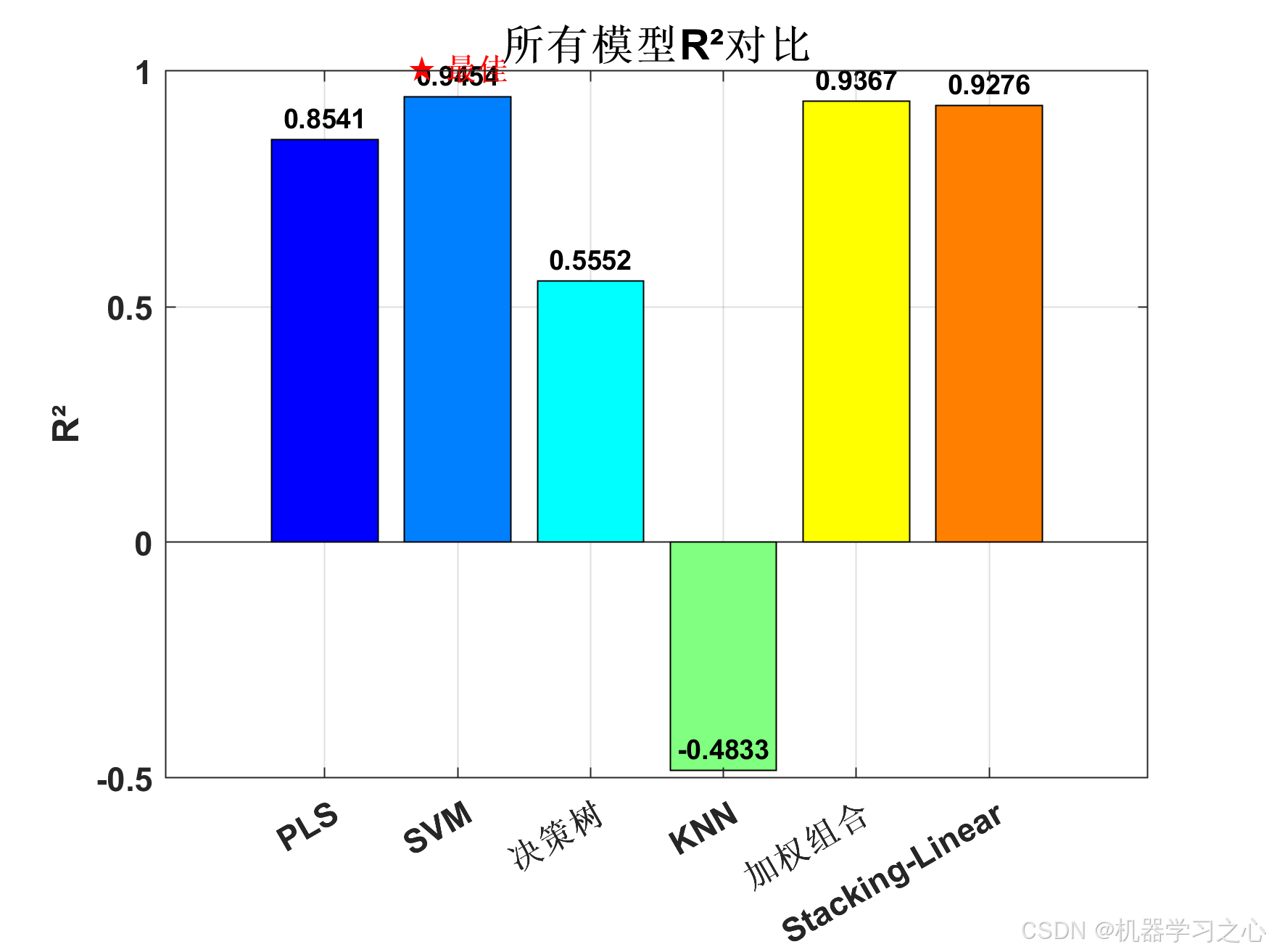
{'PLS' } 0.098532 0.3139 0.22649 0.85412 0.74472 136.37
{'SVM' } 0.036868 0.19201 0.144 0.94542 0.90448 53.393
{'决策树' } 0.30047 0.54815 0.4317 0.55516 0.22153 174.11
{'KNN' } 1.0019 1.001 0.81251 -0.48332 -1.5958 283.99
{'加权组合' } 0.042745 0.20675 0.16626 0.93672 0.88925 61.93
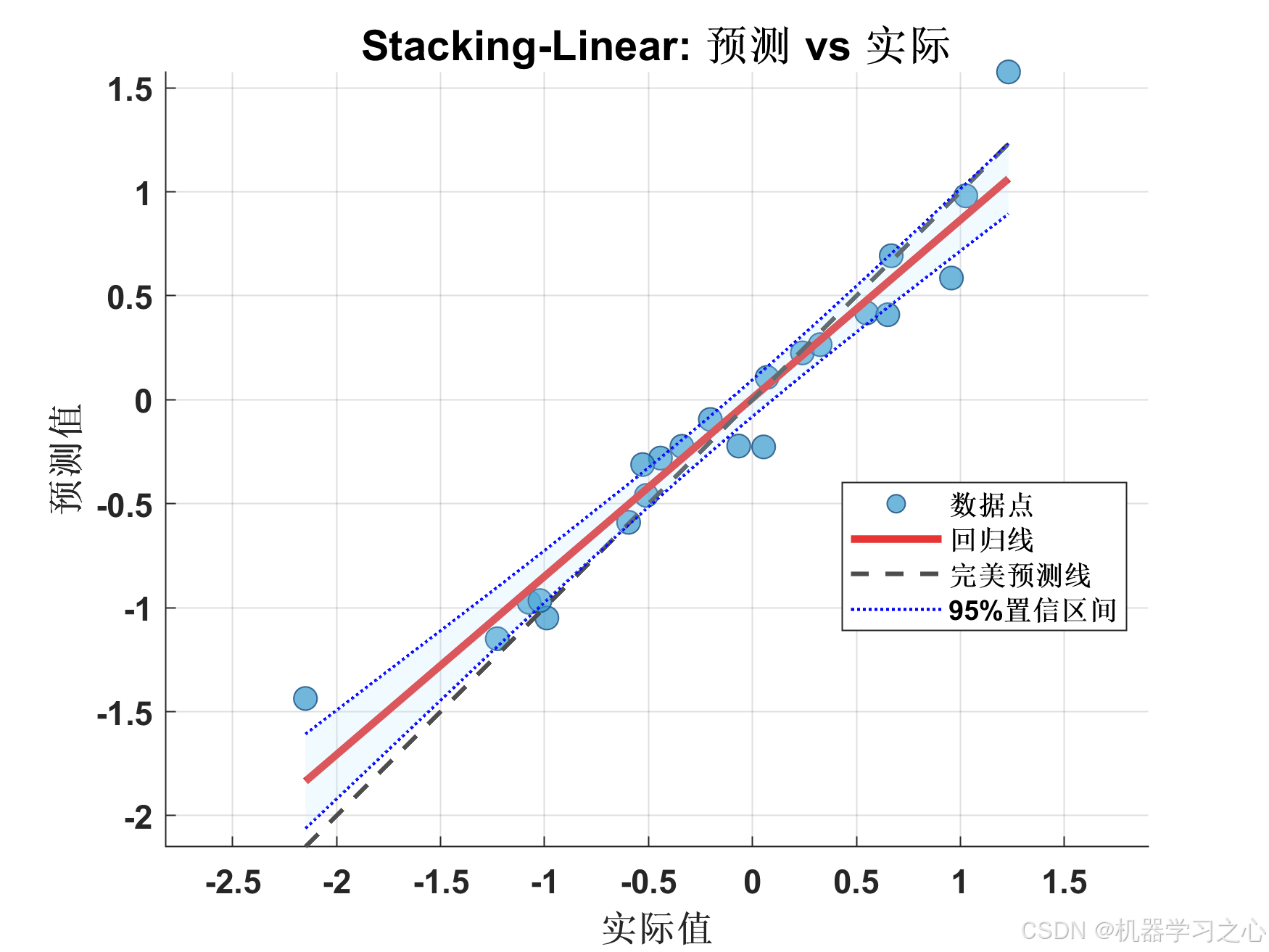
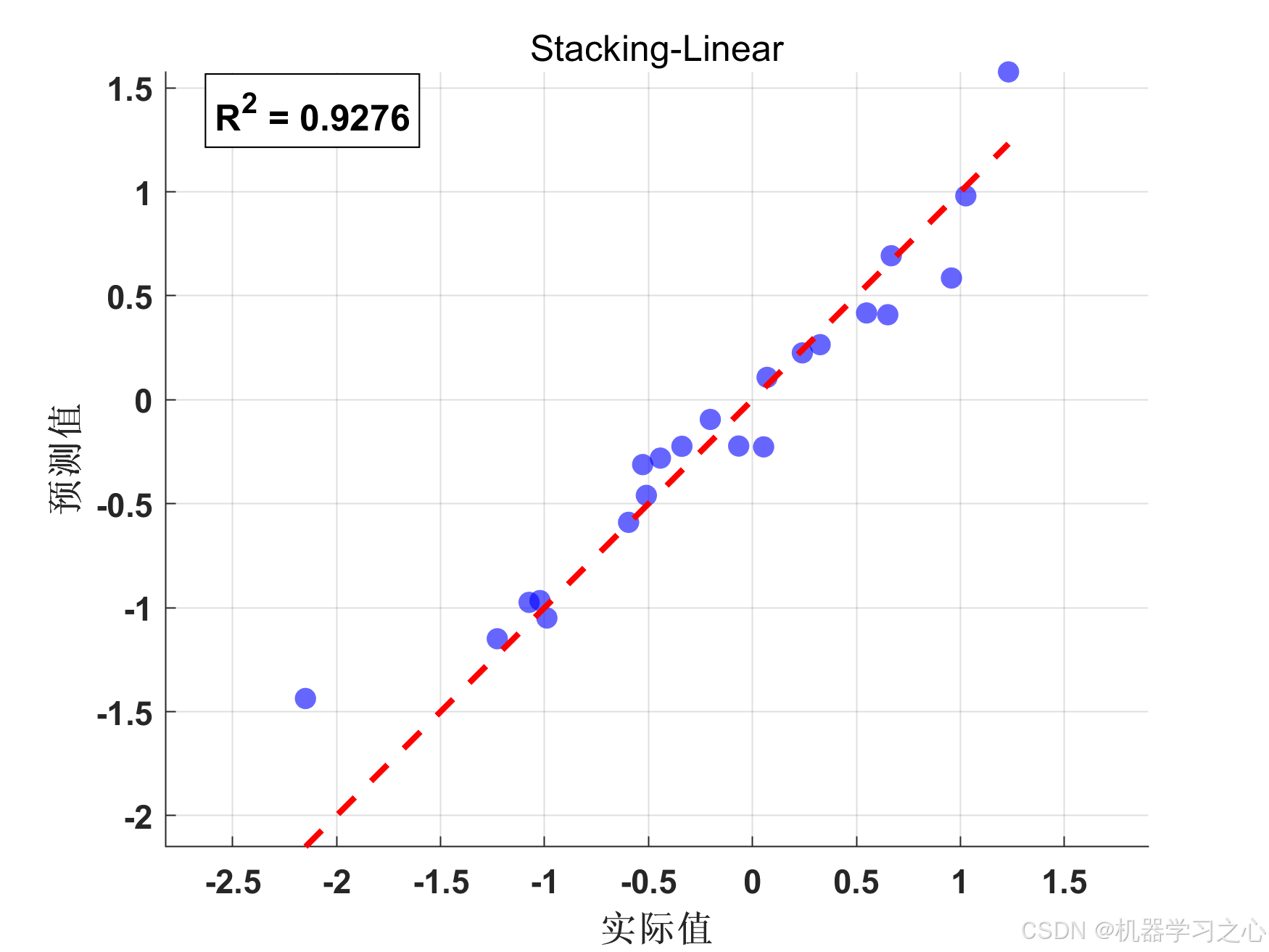
{'Stacking-Linear'} 0.048899 0.22113 0.15342 0.92761 0.87331 54.919
最佳模型: SVM (MSE: 0.036868, R²: 0.9454)
========== Stacking性能提升分析 ==========
相对于 PLS:
MSE提升: 50.37% (从 0.098532 降到 0.048899)
R²提升: 8.60% (从 0.8541 提升到 0.9276)
✓ Stacking性能优于PLS
相对于 SVM:
MSE提升: -32.63% (从 0.036868 降到 0.048899)
R²提升: -1.88% (从 0.9454 提升到 0.9276)
✗ SVM性能优于Stacking
相对于 决策树:
MSE提升: 83.73% (从 0.300466 降到 0.048899)
R²提升: 67.09% (从 0.5552 提升到 0.9276)
✓ Stacking性能优于决策树
相对于 KNN:
MSE提升: 95.12% (从 1.001909 降到 0.048899)
R²提升: 291.92% (从 -0.4833 提升到 0.9276)
✓ Stacking性能优于KNN
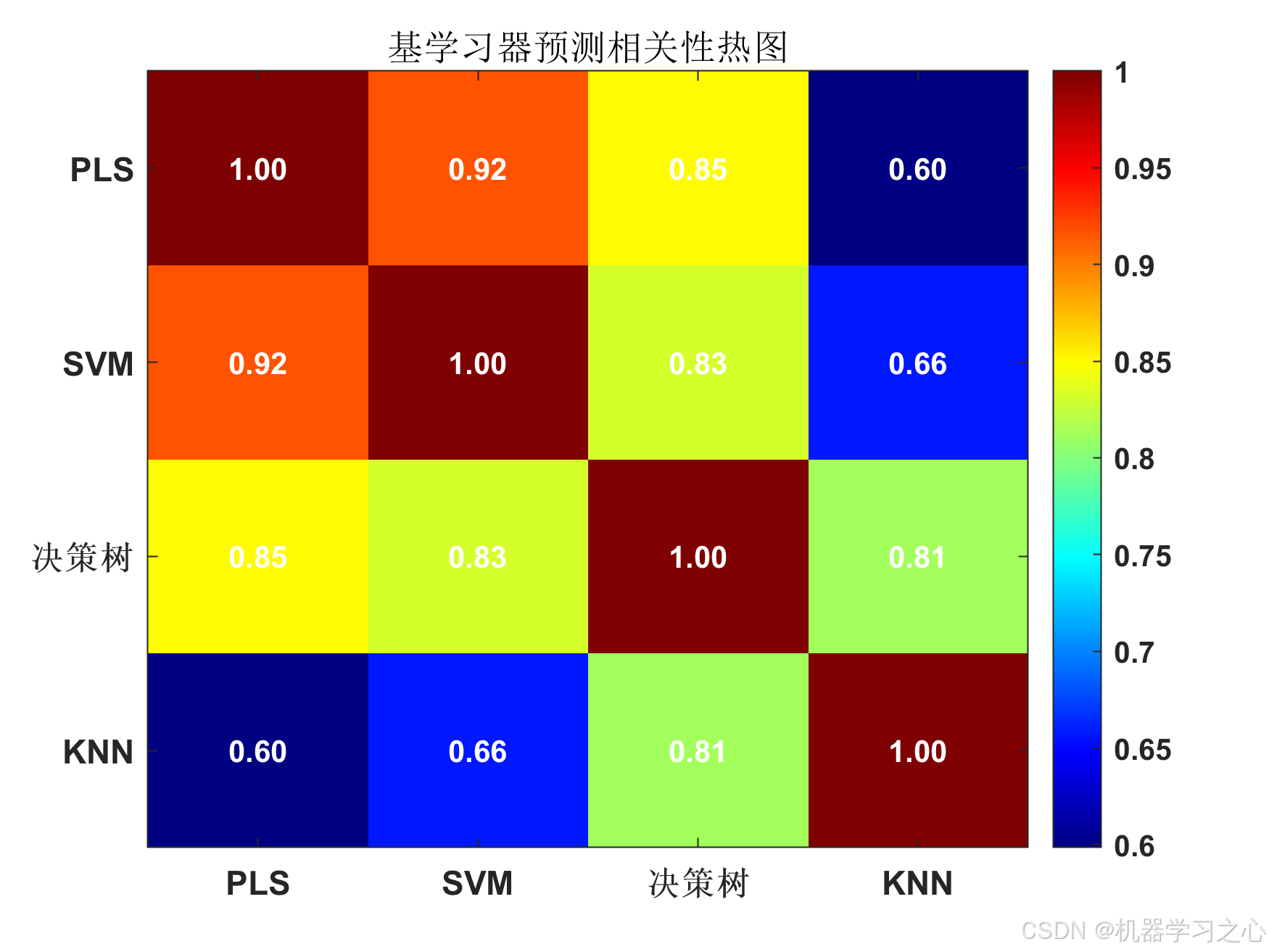
========== Stacking性能深入分析 ==========
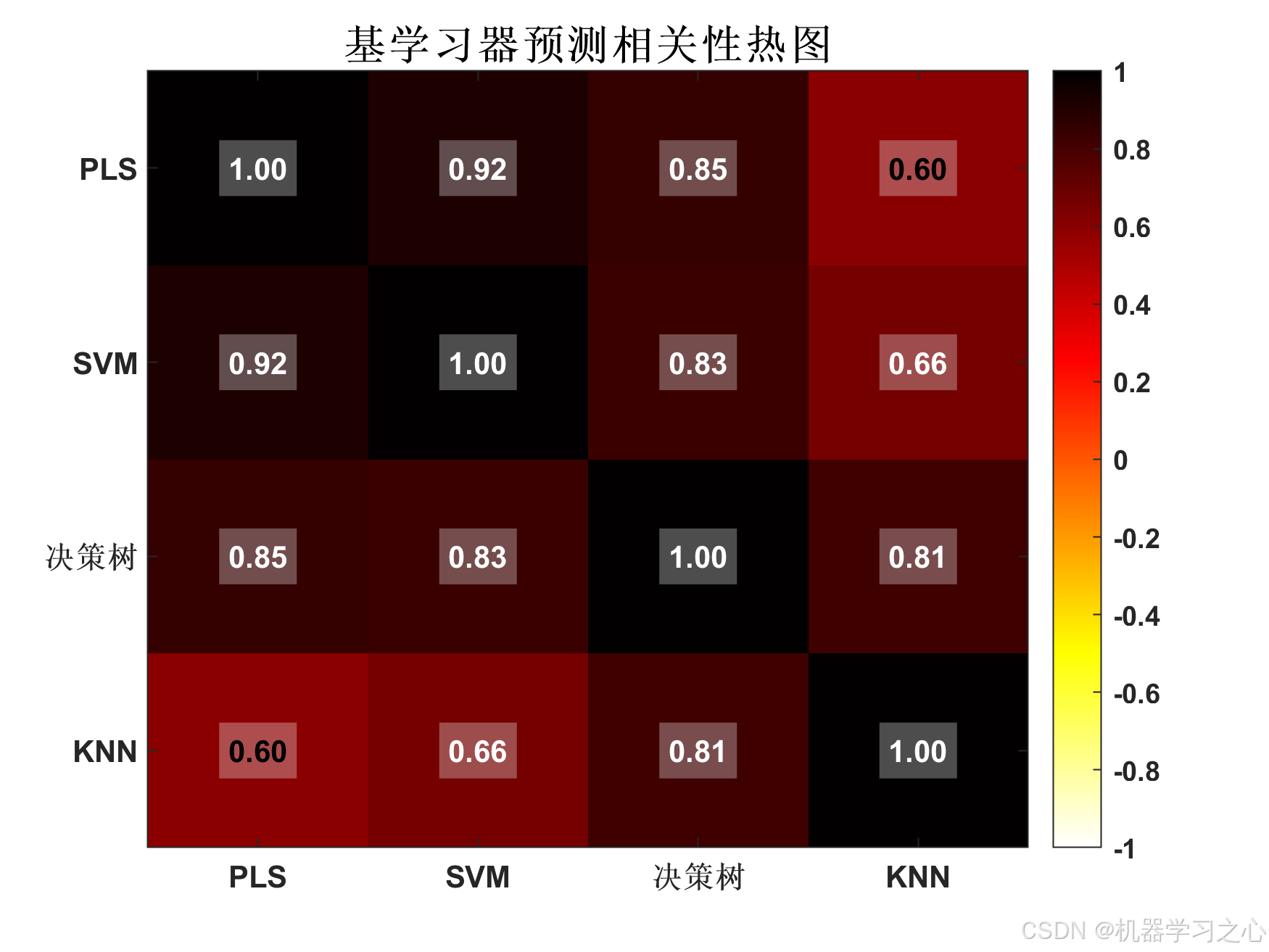
基学习器预测结果之间的相关系数矩阵:
PLS SVM 决策树 KNN
_______ _______ _______ _______
PLS 1 0.91675 0.84994 0.59847
SVM 0.91675 1 0.83215 0.65719
决策树 0.84994 0.83215 1 0.8133
KNN 0.59847 0.65719 0.8133 1
平均相关系数: 0.7780
提示: 基学习器预测中度相关(0.5-0.8),Stacking可能有一定收益
基学习器多样性分析(误差与其他预测的相关性):
PLS: 0.1034
SVM: 0.3242
决策树: 0.2940
KNN: 0.2462
公众号:机器学习之心HML
公众号:机器学习之心HML
公众号:机器学习之心HML
========== 可视化结果 ==========
可视化完成!
========== 模型保存 ==========
优化后的Stacking模型已保存到 optimized_stacking_model.mat
最佳模型: Stacking-Linear
测试集R²: 0.9276
已保存: 结果/图1.png
已保存: 结果/图2.png
已保存: 结果/图3.png
已保存: 结果/图4.png
已保存: 结果/图5.png
已保存: 结果/图6.png
已保存: 结果/图7.png
已保存: 结果/图8.png
已保存: 结果/图9.png
已保存: 结果/图10.png
已保存: 结果/图11.png
已保存: 结果/图12.png
已保存: 结果/图13.png
已保存: 结果/图14.png
已保存: 结果/图15.png
>>