从0开始学算法——第十九天（并查集）

写在开头的话

学习了昨天的分治算法，今天让我们一起来学习一下并查集的相关知识吧

第一节

知识点：

（1）并查集基础（2）并查集的路径压缩（3）路径压缩和按秩合并等优化策略

并查集基础

基础知识

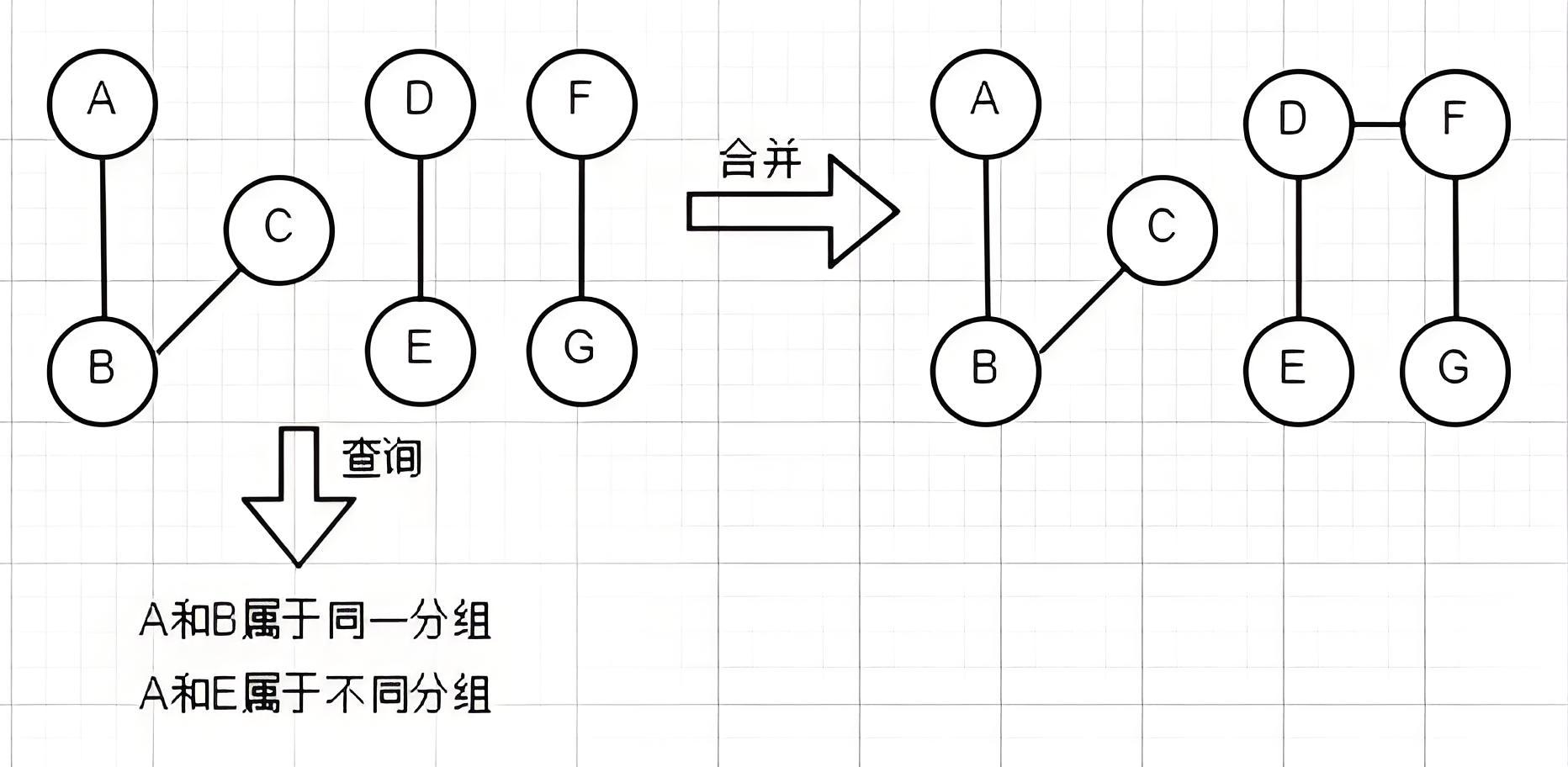
并查集是一种用来管理元素分组的数据结构。它主要支持两种操作：查找和合并。

在并查集中，每个元素都有一个代表元素（也称为根节点），代表元素可以用来标识元素所属的分组。初始状态下，每个元素都是单独的一组，每个元素的代表元素就是它自己。

• 查找操作用于确定某个元素所属的分组，通常是通过递归或迭代地沿着元素的父节点链向上查找，直到找到代表元素。

• 合并操作用于合并两个分组，即将两个分组的代表元素连接起来，使它们成为同一个分组。

并查集常用于解决一些集合类问题，如判断图中的连通性、判断无向图中是否存在环路、图像分割等。

图示

并查集的应用

并查集在解决各种问题中都有广泛的应用，其中一些典型的应用包括：

• 连通性判断：在图论中，可以使用并查集来判断无向图中的节点是否连通。通过将每条边的两个端点所在的集合合并，可以快速判断两个节点是否属于同一个连通分量。

• 最小生成树算法（Kruskal算法）：Kruskal算法是一种常用的最小生成树算法，它通过不断选择图中的边来构建最小生成树。在算法中需要频繁地判断两个节点是否在同一个连通分量中，这时可以利用并查集来实现高效的判断操作。

• 图像分割：在图像处理领域，可以使用并查集来实现图像分割。通过将图像中的像素看作是图中的节点，将相邻且具有相似特征的像素合并到同一个分组中，可以实现图像的分割和区域的提取。

• 区间合并问题：在处理区间合并问题时，可以使用并查集来合并相交或相邻的区间。通过将区间的端点看作是并查集中的元素，并按照端点的位置进行合并操作，可以快速地合并区间。

• 动态连通性问题：在动态连通性问题中，需要支持动态地添加和删除节点，并且要求能够快速地判断两个节点是否连通。并查集可以很好地满足这些需求，通过合并操作和查找操作可以实现动态连通性的维护。

常见的实现方式

基于数组的实现

• 使用一个数组 parent[] 来保存每个元素的父节点，初始时每个元素的父节点都指向自己。
• find(x) 操作通过递归或迭代地查找元素 x 的根节点，直到找到根节点为止，并返回根节点的索引。
• union(x, y) 操作将元素 x 所在的分组的根节点连接到元素 y 所在的分组的根节点上，即将 parent[find(x)] 设置为 find(y)。

基于树的实现

• 使用一棵树来表示每个分组，其中每个节点表示一个元素，根节点表示该分组的代表元素。
• find(x) 操作通过沿着元素 x 的父节点链向上查找，直到找到根节点，返回根节点。
• union(x, y) 操作将元素 x 所在的树连接到元素 y 所在的树上，即将 x 的根节点的父节点设置为 y 的根节点。

在实际应用中，可以根据具体问题选择不同的实现方式，并根据性能要求进行优化，比如路径压缩和按秩合并等技术。

代码实现

C++代码实现

#include <iostream>
#include <vector>

using namespace std;

class UnionFind {
private:
    vector<int> parent; // 用于保存每个元素的父节点

public:
    UnionFind(int n) {
        parent.resize(n);
        // 初始化，每个元素的父节点为自己
        for (int i = 0; i < n; ++i) {
            parent[i] = i;
        }
    }

    // 查找元素x所属的分组的根节点
    int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]); // 路径压缩，将x的父节点设为根节点
        }
        return parent[x];
    }

    // 合并元素x所在的分组和元素y所在的分组
    void unionSets(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            parent[rootX] = rootY; // 将x所在分组的根节点设为y所在分组的根节点
        }
    }
};

int main() {
    // 创建一个并查集，包含10个元素
    UnionFind uf(10);
    // 合并一些元素
    uf.unionSets(0, 1);
    uf.unionSets(2, 3);
    uf.unionSets(4, 5);
    uf.unionSets(6, 7);
    uf.unionSets(8, 9);

    // 查找一些元素的根节点并输出
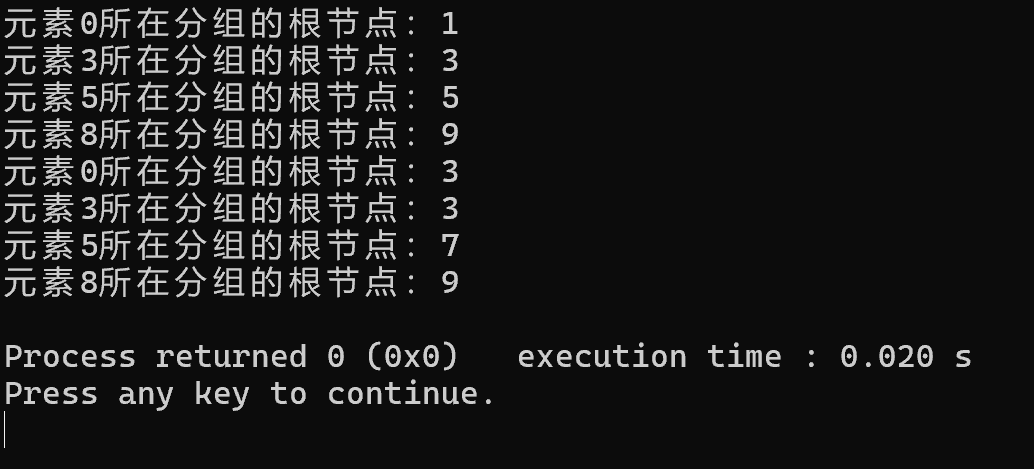
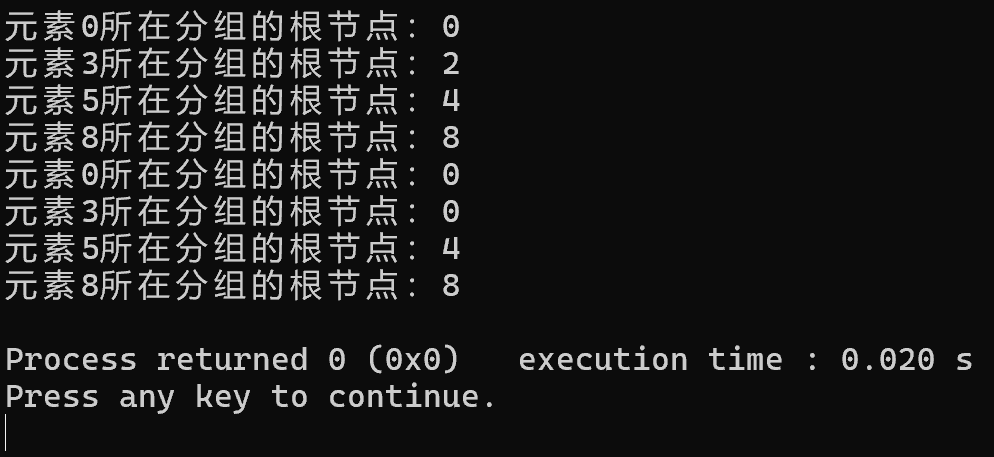
    cout << "元素0所在分组的根节点：" << uf.find(0) << endl;
    cout << "元素3所在分组的根节点：" << uf.find(3) << endl;
    cout << "元素5所在分组的根节点：" << uf.find(5) << endl;
    cout << "元素8所在分组的根节点：" << uf.find(8) << endl;

    // 合并一些分组
    uf.unionSets(1, 3);
    uf.unionSets(5, 7);

    // 再次查找元素的根节点并输出
    cout << "元素0所在分组的根节点：" << uf.find(0) << endl;
    cout << "元素3所在分组的根节点：" << uf.find(3) << endl;
    cout << "元素5所在分组的根节点：" << uf.find(5) << endl;
    cout << "元素8所在分组的根节点：" << uf.find(8) << endl;

    return 0;
}

Java代码实现

import java.util.Arrays;

public class UnionFind {
    private int[] parent; // 用于保存每个元素的父节点

    public UnionFind(int n) {
        parent = new int[n];
        // 初始化，每个元素的父节点为自己
        for (int i = 0; i < n; ++i) {
            parent[i] = i;
        }
    }

    // 查找元素x所属的分组的根节点
    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]); // 路径压缩，将x的父节点设为根节点
        }
        return parent[x];
    }

    // 合并元素x所在的分组和元素y所在的分组
    public void unionSets(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            parent[rootX] = rootY; // 将x所在分组的根节点设为y所在分组的根节点
        }
    }

    public static void main(String[] args) {
        // 创建一个并查集，包含10个元素
        UnionFind uf = new UnionFind(10);
        // 合并一些元素
        uf.unionSets(0, 1);
        uf.unionSets(2, 3);
        uf.unionSets(4, 5);
        uf.unionSets(6, 7);
        uf.unionSets(8, 9);

        // 查找一些元素的根节点并输出
        System.out.println("元素0所在分组的根节点：" + uf.find(0));
        System.out.println("元素3所在分组的根节点：" + uf.find(3));
        System.out.println("元素5所在分组的根节点：" + uf.find(5));
        System.out.println("元素8所在分组的根节点：" + uf.find(8));

        // 合并一些分组
        uf.unionSets(1, 3);
        uf.unionSets(5, 7);

        // 再次查找元素的根节点并输出
        System.out.println("元素0所在分组的根节点：" + uf.find(0));
        System.out.println("元素3所在分组的根节点：" + uf.find(3));
        System.out.println("元素5所在分组的根节点：" + uf.find(5));
        System.out.println("元素8所在分组的根节点：" + uf.find(8));
    }
}

Python代码实现

class UnionFind:
    def __init__(self, n):
        self.parent = [i for i in range(n)]  # 用于保存每个元素的父节点

    # 查找元素x所属的分组的根节点
    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])  # 路径压缩，将x的父节点设为根节点
        return self.parent[x]

    # 合并元素x所在的分组和元素y所在的分组
    def union_sets(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x != root_y:
            self.parent[root_x] = root_y  # 将x所在分组的根节点设为y所在分组的根节点

# 创建一个并查集，包含10个元素
uf = UnionFind(10)
# 合并一些元素
uf.union_sets(0, 1)
uf.union_sets(2, 3)
uf.union_sets(4, 5)
uf.union_sets(6, 7)
uf.union_sets(8, 9)

# 查找一些元素的根节点并输出
print("元素0所在分组的根节点：", uf.find(0))
print("元素3所在分组的根节点：", uf.find(3))
print("元素5所在分组的根节点：", uf.find(5))
print("元素8所在分组的根节点：", uf.find(8))

# 合并一些分组
uf.union_sets(1, 3)
uf.union_sets(5, 7)

# 再次查找元素的根节点并输出
print("元素0所在分组的根节点：", uf.find(0))
print("元素3所在分组的根节点：", uf.find(3))
print("元素5所在分组的根节点：", uf.find(5))
print("元素8所在分组的根节点：", uf.find(8))

运行结果

路径压缩优化

简单介绍

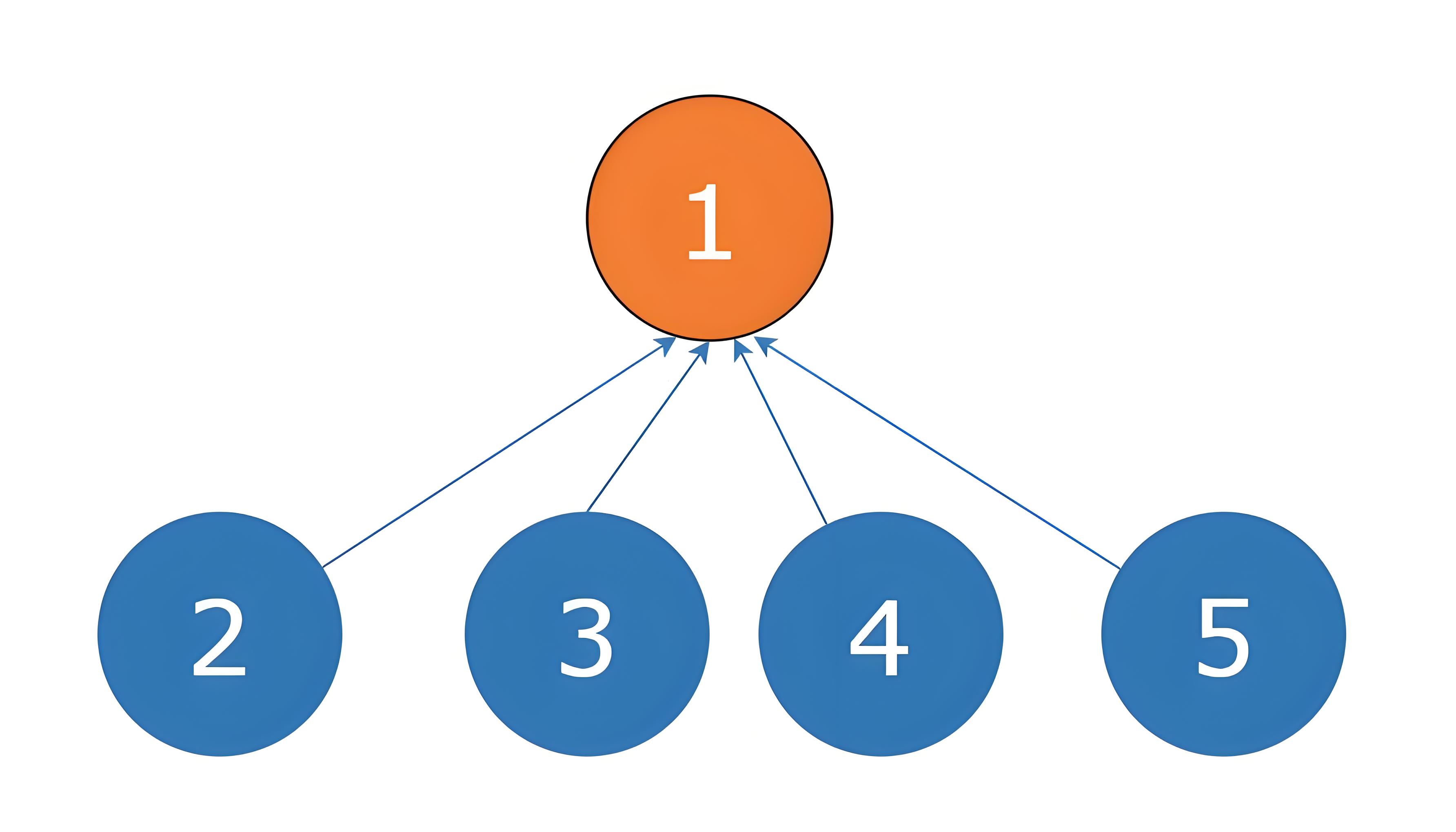
并查集的路径压缩是一种优化策略，旨在缩短查找操作的路径长度，从而提高整体的性能。在进行查找操作时，路径压缩会使得树中的每个节点直接指向根节点，以减少后续查找相同元素时所需的遍历路径长度。

• 基本的路径压缩算法是在查找操作中，将经过的每个节点直接连接到根节点上，从而使得整个路径上的节点都直接指向根节点。这样做可以减少后续查找相同元素时所需的时间，因为路径被压缩成了更短的形式。

• 路径压缩的实现通常通过递归或迭代来完成。在递归实现中，查找操作会递归地调用自身，直到找到根节点，并在回溯的过程中更新每个节点的父节点，使其直接指向根节点。在迭代实现中，通过循环迭代将每个节点直接连接到根节点上，直到找到根节点为止。

路径压缩可以显著提高并查集的性能，尤其是在进行多次查找操作时。通过减少路径长度，路径压缩可以降低查找操作的时间复杂度，使得并查集更加高效。

图示

代码实现

C++代码实现

//递归方式实现
int find(int x){
    return x==father[x]?x:father[x]=find(father[x]);
} 
//循环方式实现
int find(int x){//相比之下，递归的写法真的是浑然天成
    int k=x,temp;
    while(k^father[k]) k=father[k];
    while(x^k){
        temp=father[x];
        father[x]=k;
        x=temp;
    }
    return k;
}

Java代码实现

class UnionFind {
    private int[] parent;

    public UnionFind(int n) {
        parent = new int[n];
        for (int i = 0; i < n; ++i)
            parent[i] = i;
    }

    private int find(int x) {
        return x == parent[x] ? x : (parent[x] = find(parent[x]));
    }

    public int findRoot(int x) {
        return find(x);
    }
}
class UnionFind2 {
    private int[] parent;

    public UnionFind(int n) {
        parent = new int[n];
        for (int i = 0; i < n; ++i)
            parent[i] = i;
    }

    private int find(int x) {
        int k = x;
        while (k != parent[k]) k = parent[k];
        while (x != k) {
            int temp = parent[x];
            parent[x] = k;
            x = temp;
        }
        return k;
    }

    public int findRoot(int x) {
        return find(x);
    }
}

Python代码实现

class UnionFind:
    def __init__(self, n):
        self.parent = [i for i in range(n)]

    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])  # 路径压缩
        return self.parent[x]

uf = UnionFind(10)  # 创建一个包含10个元素的并查集
class UnionFind2:
    def __init__(self, n):
        self.parent = [i for i in range(n)]

    def find(self, x):
        k = x
        while k != self.parent[k]:
            k = self.parent[k]
        while x != k:
            x, self.parent[x] = self.parent[x], k  # 路径压缩
        return k

uf2 = UnionFind2(10)  # 创建一个包含10个元素的并查集2

按秩合并优化

简单介绍

并查集的按秩合并是一种优化策略，旨在降低树的高度，从而提高查找操作的效率。在并查集中，树的高度会影响到查找操作的时间复杂度，因此通过按秩合并可以有效地降低树的高度。

基本思想

按秩合并的基本思想是，将具有较小秩（即树的高度）的树合并到具有较大秩的树上。这样做的目的是尽可能地减小合并后树的高度，从而降低查找操作的时间复杂度。在合并操作中，需要比较两个根节点的秩，然后将较小秩的根节点连接到较大秩的根节点上，以确保树的高度尽可能小。

当两棵树的秩相同时，可以任意选择其中一棵树的根节点作为合并后的根节点，并将另一棵树连接到该根节点上。此时，被连接的树的秩需要增加1，以保持合并后树的高度平衡。

举例说明

我们来看下面两个集合合并的问题：

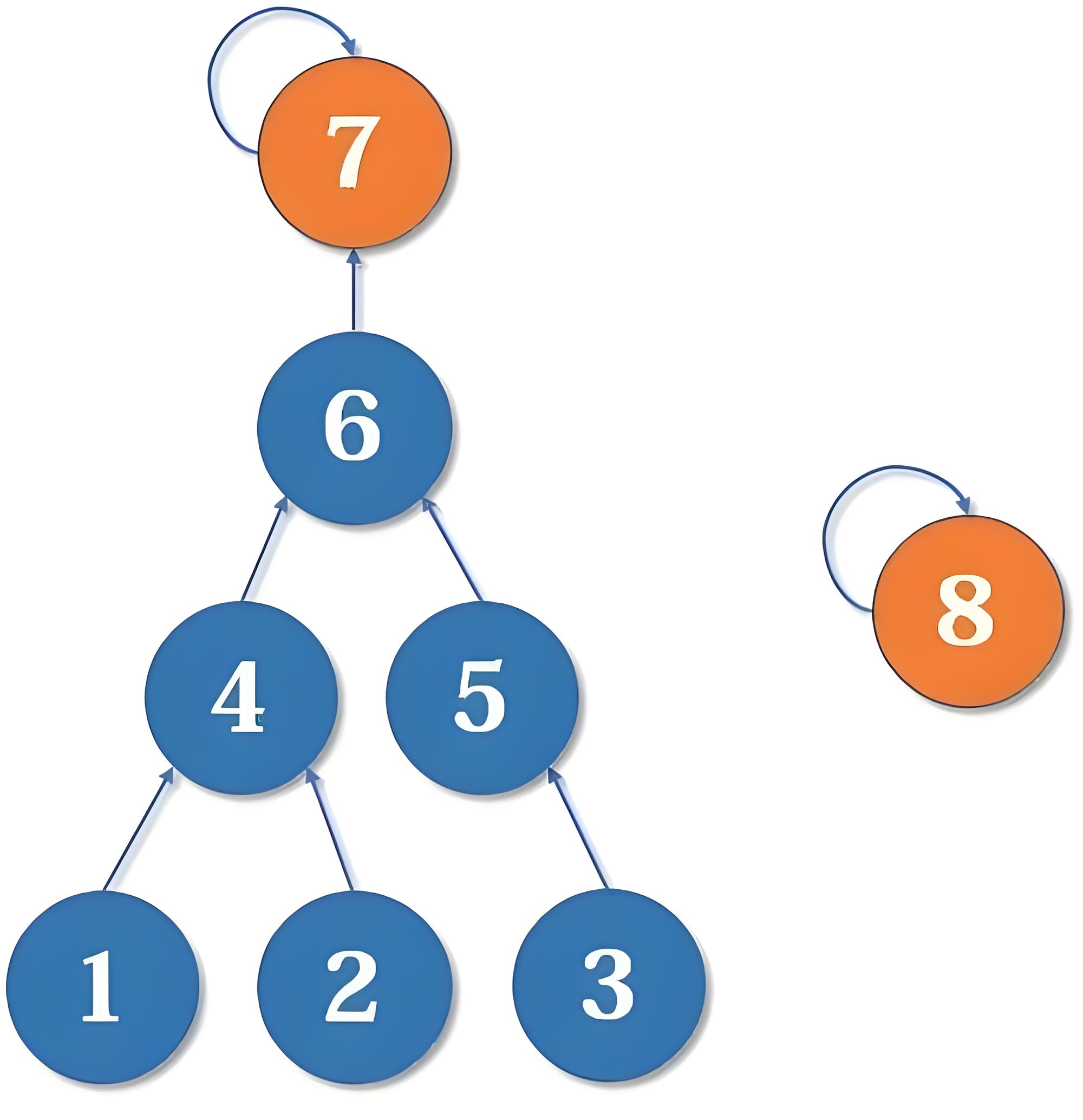
对于这两个集合合并，我们是把 8设为 7 的父结点好，还是 7 设为 8 的父节点：显然是后者。采用前者的合并方式会使树的深度变深，查询的路径也会变长。相反，后者不存在这个问题。

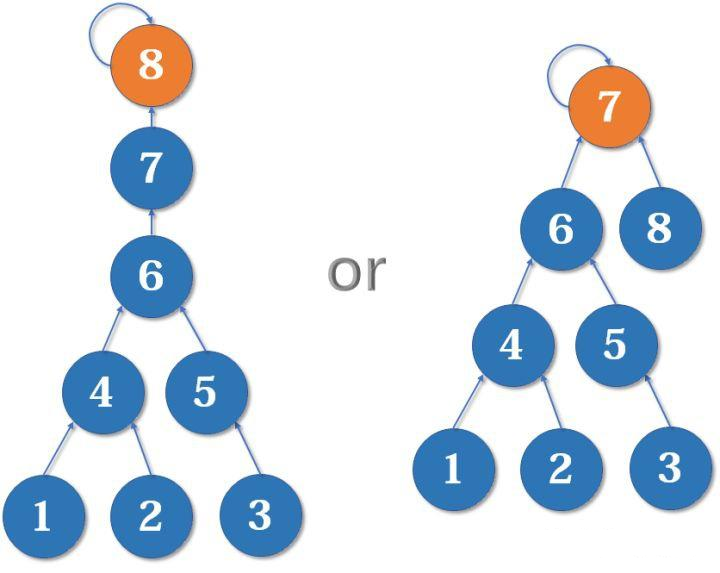
一般以树高作为秩：定义 rank 数组，初始化全为 0，find() 操作不改变秩，而执行 union 操作时，则需比较 rank 值的大小，将 rank 较大的集合的代表元素作为父亲结点，然后合并（若秩相同则任选一个集合的代表元素作为父亲结点）。

代码实现

C++代码实现

#include <iostream>
#include <vector>

using namespace std;

class UnionFind {
private:
    vector<int> parent; // 用于保存每个元素的父节点
    vector<int> rank;   // 用于保存每个根节点所在树的高度（秩）

public:
    UnionFind(int n) {
        parent.resize(n);
        rank.resize(n, 0); // 初始时每棵树的高度为0
        // 初始化，每个元素的父节点为自己
        for (int i = 0; i < n; ++i) {
            parent[i] = i;
        }
    }

    // 查找元素x所属的分组的根节点
    int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]); // 路径压缩，将x的父节点设为根节点
        }
        return parent[x];
    }

    // 合并元素x所在的分组和元素y所在的分组
    void unionSets(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            // 将高度较小的树合并到高度较大的树上，以减小整体树的高度
            if (rank[rootX] < rank[rootY]) {
                parent[rootX] = rootY;
            } else if (rank[rootX] > rank[rootY]) {
                parent[rootY] = rootX;
            } else {
                parent[rootY] = rootX;
                rank[rootX]++; // 如果两棵树高度相同，则合并后的树高度加1
            }
        }
    }
};

int main() {
    // 创建一个并查集，包含10个元素
    UnionFind uf(10);
    // 合并一些元素
    uf.unionSets(0, 1);
    uf.unionSets(2, 3);
    uf.unionSets(4, 5);
    uf.unionSets(6, 7);
    uf.unionSets(8, 9);

    // 查找一些元素的根节点并输出
    cout << "元素0所在分组的根节点：" << uf.find(0) << endl;
    cout << "元素3所在分组的根节点：" << uf.find(3) << endl;
    cout << "元素5所在分组的根节点：" << uf.find(5) << endl;
    cout << "元素8所在分组的根节点：" << uf.find(8) << endl;

    // 合并一些分组
    uf.unionSets(1, 3);
    uf.unionSets(5, 7);

    // 再次查找元素的根节点并输出
    cout << "元素0所在分组的根节点：" << uf.find(0) << endl;
    cout << "元素3所在分组的根节点：" << uf.find(3) << endl;
    cout << "元素5所在分组的根节点：" << uf.find(5) << endl;
    cout << "元素8所在分组的根节点：" << uf.find(8) << endl;

    return 0;
}

Java代码实现

import java.util.Arrays;

public class UnionFind {
    private int[] parent; // 用于保存每个元素的父节点
    private int[] rank;   // 用于保存每个根节点所在树的高度（秩）

    public UnionFind(int n) {
        parent = new int[n];
        rank = new int[n];
        // 初始化，每个元素的父节点为自己，树的高度为0
        for (int i = 0; i < n; ++i) {
            parent[i] = i;
            rank[i] = 0;
        }
    }

    // 查找元素x所属的分组的根节点
    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]); // 路径压缩，将x的父节点设为根节点
        }
        return parent[x];
    }

    // 合并元素x所在的分组和元素y所在的分组
    public void unionSets(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            // 将高度较小的树合并到高度较大的树上，以减小整体树的高度
            if (rank[rootX] < rank[rootY]) {
                parent[rootX] = rootY;
            } else if (rank[rootX] > rank[rootY]) {
                parent[rootY] = rootX;
            } else {
                parent[rootY] = rootX;
                rank[rootX]++; // 如果两棵树高度相同，则合并后的树高度加1
            }
        }
    }

    public static void main(String[] args) {
        // 创建一个并查集，包含10个元素
        UnionFind uf = new UnionFind(10);
        // 合并一些元素
        uf.unionSets(0, 1);
        uf.unionSets(2, 3);
        uf.unionSets(4, 5);
        uf.unionSets(6, 7);
        uf.unionSets(8, 9);

        // 查找一些元素的根节点并输出
        System.out.println("元素0所在分组的根节点：" + uf.find(0));
        System.out.println("元素3所在分组的根节点：" + uf.find(3));
        System.out.println("元素5所在分组的根节点：" + uf.find(5));
        System.out.println("元素8所在分组的根节点：" + uf.find(8));

        // 合并一些分组
        uf.unionSets(1, 3);
        uf.unionSets(5, 7);

        // 再次查找元素的根节点并输出
        System.out.println("元素0所在分组的根节点：" + uf.find(0));
        System.out.println("元素3所在分组的根节点：" + uf.find(3));
        System.out.println("元素5所在分组的根节点：" + uf.find(5));
        System.out.println("元素8所在分组的根节点：" + uf.find(8));
    }
}

Python代码实现

class UnionFind:
    def __init__(self, n):
        self.parent = list(range(n))  # 用于保存每个元素的父节点
        self.rank = [0] * n  # 用于保存每个根节点所在树的高度（秩）

    # 查找元素x所属的分组的根节点
    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])  # 路径压缩，将x的父节点设为根节点
        return self.parent[x]

    # 合并元素x所在的分组和元素y所在的分组
    def union_sets(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x != root_y:
            # 将高度较小的树合并到高度较大的树上，以减小整体树的高度
            if self.rank[root_x] < self.rank[root_y]:
                self.parent[root_x] = root_y
            elif self.rank[root_x] > self.rank[root_y]:
                self.parent[root_y] = root_x
            else:
                self.parent[root_y] = root_x
                self.rank[root_x] += 1  # 如果两棵树高度相同，则合并后的树高度加1

# 创建一个并查集，包含10个元素
uf = UnionFind(10)
# 合并一些元素
uf.union_sets(0, 1)
uf.union_sets(2, 3)
uf.union_sets(4, 5)
uf.union_sets(6, 7)
uf.union_sets(8, 9)

# 查找一些元素的根节点并输出
print("元素0所在分组的根节点：", uf.find(0))
print("元素3所在分组的根节点：", uf.find(3))
print("元素5所在分组的根节点：", uf.find(5))
print("元素8所在分组的根节点：", uf.find(8))

# 合并一些分组
uf.union_sets(1, 3)
uf.union_sets(5, 7)

# 再次查找元素的根节点并输出
print("元素0所在分组的根节点：", uf.find(0))
print("元素3所在分组的根节点：", uf.find(3))
print("元素5所在分组的根节点：", uf.find(5))
print("元素8所在分组的根节点：", uf.find(8))

运行结果

简单总结

在本节中，我们学习了并查集。并查集是一种非常重要的数据结构，在解决一些与集合、连接性相关的问题时非常有用。掌握了并查集这一数据结构，对于解决一些复杂的连通性问题将会大有裨益。

第二节

知识点：

（1）连通分量问题（2）朋友圈问题（3）并查集求岛屿数量

连通分量问题

简单介绍

连通分量是图论中一个重要的概念，特别是在图的连通性分析和网络分析中。在图中，一个连通分量指的是一个子图，其中的任意两个顶点都是连通的，也就是说存在一条路径将它们连接起来。如果一个图只有一个连通分量，那么这个图就是连通图。

连通分量的概念也可以应用在非连通图中。一个非连通图可以被分解成多个互不相连的连通分量，每个连通分量都是一个连通子图。这些连通分量之间没有路径相连，它们是图的极大连通子图，也就是不能再添加任何顶点或边使得它们变得更大。

连通分量应用

连通分量在实际应用中有广泛的用途，比如在社交网络分析中，可以用连通分量来表示社交网络中的不同社群或群体；在电力系统或通信网络中，可以用连通分量来表示电力或信息的传输路径；在地理信息系统中，可以用连通分量来表示地理空间中的连通区域等等。

算法实现

在算法中，常用的一种方法是通过深度优先搜索（DFS）或广度优先搜索（BFS）来找出图中的所有连通分量。另外，还有一种经典的数据结构和算法叫做并查集，也可以用来高效地处理连通分量的相关问题，比如判断两个顶点是否属于同一个连通分量，或者合并两个连通分量等。

代码实现

C++代码实现

#include <iostream>
#include <vector>

using namespace std;

class DisjointSet {
private:
    vector<int> parent;
public:
    DisjointSet(int n) {
        parent.resize(n);
        for (int i = 0; i < n; ++i) {
            parent[i] = i;
        }
    }

    int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    void unite(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            parent[rootX] = rootY;
        }
    }
};

int main() {
    int n = 6;
    DisjointSet ds(n);

    ds.unite(0, 1);
    ds.unite(1, 2);
    ds.unite(3, 4);

    cout << "0 and 2 are in the same connected component: " << (ds.find(0) == ds.find(2)) << endl;
    cout << "0 and 4 are in the same connected component: " << (ds.find(0) == ds.find(4)) << endl;

    return 0;
}

Java代码实现

import java.util.Arrays;

class DisjointSet {
    private int[] parent;

    public DisjointSet(int n) {
        parent = new int[n];
        Arrays.fill(parent, -1);
    }

    public int find(int x) {
        if (parent[x] < 0) {
            return x;
        }
        return parent[x] = find(parent[x]);
    }

    public void unite(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            parent[rootY] = rootX;
        }
    }
}

public class Main {
    public static void main(String[] args) {
        int n = 6;
        DisjointSet ds = new DisjointSet(n);

        ds.unite(0, 1);
        ds.unite(1, 2);
        ds.unite(3, 4);

        System.out.println("0 and 2 are in the same connected component: " + (ds.find(0) == ds.find(2)));
        System.out.println("0 and 4 are in the same connected component: " + (ds.find(0) == ds.find(4)));
    }
}

Python代码实现

class DisjointSet:
    def __init__(self, n):
        self.parent = [-1] * n

    def find(self, x):
        if self.parent[x] < 0:
            return x
        self.parent[x] = self.find(self.parent[x])
        return self.parent[x]

    def unite(self, x, y):
        rootX = self.find(x)
        rootY = self.find(y)
        if rootX != rootY:
            self.parent[rootY] = rootX

def main():
    n = 6
    ds = DisjointSet(n)

    ds.unite(0, 1)
    ds.unite(1, 2)
    ds.unite(3, 4)

    print("0 and 2 are in the same connected component:", ds.find(0) == ds.find(2))
    print("0 and 4 are in the same connected component:", ds.find(0) == ds.find(4))

if __name__ == "__main__":
    main()

运行结果

朋友圈问题

问题描述

已知有 n 个人和 m 对好友关系。如果 A 和 B 是好友，B 和 C 也是好友，那么 A 和 C 也是好友。问这 n 个人中一共有多少个朋友圈。

思路分析

我们可以利用并查集来解决这个问题。将已经确认好友关系的两人放入同一个并查集中，最后检查集合的个数即可。

代码实现

C++代码实现

#include <iostream>
#include <vector>

using namespace std;

class DisjointSet {
private:
    vector<int> parent;
    vector<int> rank;
    int count;
public:
    DisjointSet(int n) {
        parent.resize(n);
        rank.resize(n, 0);
        count = n;
        for (int i = 0; i < n; ++i) {
            parent[i] = i;
        }
    }

    int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    void unite(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            if (rank[rootX] < rank[rootY]) {
                swap(rootX, rootY);
            }
            parent[rootY] = rootX;
            if (rank[rootX] == rank[rootY]) {
                rank[rootX]++;
            }
            count--;
        }
    }

    int getCount() {
        return count;
    }
};

int main() {
    int n = 5; // 5 个人
    int m = 4; // 4 对好友关系
    vector<pair<int, int>> friendPairs = {{0, 1}, {1, 2}, {3, 4}, {2, 3}};

    DisjointSet ds(n);
    for (auto& pair : friendPairs) {
        ds.unite(pair.first, pair.second);
    }

    cout << "朋友圈个数：" << ds.getCount() << endl;

    return 0;
}

Java代码实现

import java.util.Arrays;

class DisjointSet {
    private int[] parent;
    private int[] rank;
    private int count;

    public DisjointSet(int n) {
        parent = new int[n];
        rank = new int[n];
        count = n;
        Arrays.fill(rank, 0);
        for (int i = 0; i < n; ++i) {
            parent[i] = i;
        }
    }

    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    public void unite(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            if (rank[rootX] < rank[rootY]) {
                int temp = rootX;
                rootX = rootY;
                rootY = temp;
            }
            parent[rootY] = rootX;
            if (rank[rootX] == rank[rootY]) {
                rank[rootX]++;
            }
            count--;
        }
    }

    public int getCount() {
        return count;
    }
}

public class Main {
    public static void main(String[] args) {
        int n = 5; // 5 个人
        int m = 4; // 4 对好友关系
        int[][] friendPairs = {{0, 1}, {1, 2}, {3, 4}, {2, 3}};

        DisjointSet ds = new DisjointSet(n);
        for (int[] pair : friendPairs) {
            ds.unite(pair[0], pair[1]);
        }

        System.out.println("朋友圈个数：" + ds.getCount());
    }
}

Python代码实现

class DisjointSet:
    def __init__(self, n):
        self.parent = list(range(n))
        self.rank = [0] * n
        self.count = n

    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]

    def unite(self, x, y):
        rootX = self.find(x)
        rootY = self.find(y)
        if rootX != rootY:
            if self.rank[rootX] < self.rank[rootY]:
                rootX, rootY = rootY, rootX
            self.parent[rootY] = rootX
            if self.rank[rootX] == self.rank[rootY]:
                self.rank[rootX] += 1
            self.count -= 1

    def getCount(self):
        return self.count

def main():
    n = 5  # 5 个人
    m = 4  # 4 对好友关系
    friendPairs = [(0, 1), (1, 2), (3, 4), (2, 3)]

    ds = DisjointSet(n)
    for pair in friendPairs:
        ds.unite(pair[0], pair[1])

    print("朋友圈个数:", ds.getCount())

if __name__ == "__main__":
    main()

运行结果

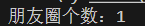
并查集求岛屿数量

问题描述

给定一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

思路描述

我们可以使用并查集来解决这个问题。我们对于一块 1，合并和它相邻的同样为 1 的块。最后检查一共有几个集合即可。

代码实现

C++代码实现

#include <iostream>
#include <vector>

using namespace std;

class UnionFind {
private:
    vector<int> parent;
    vector<int> rank;
    int count;

public:
    UnionFind(vector<vector<char>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        count = 0;
        parent.resize(m * n);
        rank.resize(m * n);
        
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == '1') {
                    parent[i * n + j] = i * n + j;
                    count++;
                }
                rank[i * n + j] = 0;
            }
        }
    }

    int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    void unite(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            if (rank[rootX] < rank[rootY]) {
                swap(rootX, rootY);
            }
            parent[rootY] = rootX;
            if (rank[rootX] == rank[rootY]) {
                rank[rootX]++;
            }
            count--;
        }
    }

    int getCount() {
        return count;
    }
};

class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        if (grid.empty() || grid[0].empty()) return 0;
        int m = grid.size(), n = grid[0].size();
        
        UnionFind uf(grid);
        
        int directions[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
        
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == '1') {
                    for (auto& dir : directions) {
                        int newRow = i + dir[0];
                        int newCol = j + dir[1];
                        if (newRow >= 0 && newRow < m && newCol >= 0 && newCol < n && grid[newRow][newCol] == '1') {
                            uf.unite(i * n + j, newRow * n + newCol);
                        }
                    }
                }
            }
        }
        
        return uf.getCount();
    }
};

int main() {
    vector<vector<char>> grid = {
        {'1', '1', '0', '0', '0'},
        {'1', '1', '0', '0', '0'},
        {'0', '0', '1', '0', '0'},
        {'0', '0', '0', '1', '1'}
    };

    Solution sol;
    cout << "Number of islands: " << sol.numIslands(grid) << endl;

    return 0;
}

Java代码实现

import java.util.Arrays;

class UnionFind {
    private int[] parent;
    private int[] rank;
    private int count;

    public UnionFind(char[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        count = 0;
        parent = new int[m * n];
        rank = new int[m * n];

        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == '1') {
                    parent[i * n + j] = i * n + j;
                    count++;
                }
                rank[i * n + j] = 0;
            }
        }
    }

    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    public void unite(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            if (rank[rootX] < rank[rootY]) {
                int temp = rootX;
                rootX = rootY;
                rootY = temp;
            }
            parent[rootY] = rootX;
            if (rank[rootX] == rank[rootY]) {
                rank[rootX]++;
            }
            count--;
        }
    }

    public int getCount() {
        return count;
    }
}

class Solution {
    public int numIslands(char[][] grid) {
        if (grid == null || grid.length == 0 || grid[0].length == 0) return 0;
        int m = grid.length, n = grid[0].length;

        UnionFind uf = new UnionFind(grid);

        int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};

        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == '1') {
                    for (int[] dir : directions) {
                        int newRow = i + dir[0];
                        int newCol = j + dir[1];
                        if (newRow >= 0 && newRow < m && newCol >= 0 && newCol < n && grid[newRow][newCol] == '1') {
                            uf.unite(i * n + j, newRow * n + newCol);
                        }
                    }
                }
            }
        }

        return uf.getCount();
    }
}

public class Main {
    public static void main(String[] args) {
        char[][] grid = {
                {'1', '1', '0', '0', '0'},
                {'1', '1', '0', '0', '0'},
                {'0', '0', '1', '0', '0'},
                {'0', '0', '0', '1', '1'}
        };

        Solution sol = new Solution();
        System.out.println("Number of islands: " + sol.numIslands(grid));
    }
}

Python代码实现

class UnionFind:
    def __init__(self, grid):
        m, n = len(grid), len(grid[0])
        self.parent = [-1] * (m * n)
        self.rank = [0] * (m * n)
        self.count = 0

        for i in range(m):
            for j in range(n):
                if grid[i][j] == '1':
                    self.parent[i * n + j] = i * n + j
                    self.count += 1

    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]

    def unite(self, x, y):
        rootX = self.find(x)
        rootY = self.find(y)
        if rootX != rootY:
            if self.rank[rootX] < self.rank[rootY]:
                rootX, rootY = rootY, rootX
            self.parent[rootY] = rootX
            if self.rank[rootX] == self.rank[rootY]:
                self.rank[rootX] += 1
            self.count -= 1

    def getCount(self):
        return self.count

class Solution:
    def numIslands(self, grid):
        if not grid or not grid[0]:
            return 0

        m, n = len(grid), len(grid[0])
        uf = UnionFind(grid)

        directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]

        for i in range(m):
            for j in range(n):
                if grid[i][j] == '1':
                    for dx, dy in directions:
                        newRow, newCol = i + dx, j + dy
                        if 0 <= newRow < m and 0 <= newCol < n and grid[newRow][newCol] == '1':
                            uf.unite(i * n + j, newRow * n + newCol)

        return uf.getCount()

grid = [
    ['1', '1', '0', '0', '0'],
    ['1', '1', '0', '0', '0'],
    ['0', '0', '1', '0', '0'],
    ['0', '0', '0', '1', '1']
]

sol = Solution()
print("Number of islands:", sol.numIslands(grid))

运行结果

简单总结

本节主要学习了几个经典的并查集的使用案例。主要是在计算连通性方面，并查集往往有很大的作用。