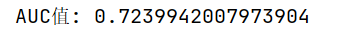决策树与回归树简介：原理、实现与应用

文章目录

- 一、决策树基本概念
- 二、决策树分类算法
- - [1. ID3算法](#1. ID3算法)
  - [2. C4.5算法](#2. C4.5算法)
  - [3. CART决策树](#3. CART决策树)
- 三、决策树回归模型
- - [1. 回归树特点](#1. 回归树特点)
  - [2. 回归树计算示例](#2. 回归树计算示例)
- 四、Scikit-learn中的决策树实现
- - [1. 分类决策树参数](#1. 分类决策树参数)
  - [2. 回归决策树参数](#2. 回归决策树参数)
- 五、Python实现示例
- - [1. 分类决策树实现](#1. 分类决策树实现)
- 六、决策树剪枝
- - [1. 剪枝的目的](#1. 剪枝的目的)
  - [2. 剪枝方法](#2. 剪枝方法)
  - [3. 预剪枝策略](#3. 预剪枝策略)
- 七、模型评估指标
- - [1. AUC-ROC曲线](#1. AUC-ROC曲线)
  - [2. AUC的优点](#2. AUC的优点)

一、决策树基本概念

决策树是一种有监督学习算法，通过对训练样本的学习建立分类或回归规则，并依据这些规则对新样本进行预测。它的核心思想是将数据从根节点逐步划分到叶子节点，形成一个树状结构。

决策树的组成

根节点：第一个节点，包含所有数据
非叶子节点（中间节点）：进行数据划分的节点
叶子节点：最终结果节点，不再继续划分

二、决策树分类算法

决策树主要有三种分类标准：

1. ID3算法

使用信息增益作为分裂标准，基于熵值衡量节点的不确定性。

熵值计算公式 ：
H ( U ) = − ∑ i = 1 n p i log ⁡ 2 p i H(U) = -\sum_{i=1}^n p_i \log_2 p_i H(U)=−∑i=1npilog2pi

熵值越小，节点越"纯"，包含的类别越单一。

2. C4.5算法

使用信息增益率作为分裂标准，解决了ID3算法倾向于选择取值较多的特征的问题。

3. CART决策树

使用基尼系数作为分裂标准，可以用于分类和回归问题。

基尼系数计算公式（二分类） ：
G i n i ( p ) = 2 p ( 1 − p ) Gini(p) = 2p(1-p) Gini(p)=2p(1−p)

三、决策树回归模型

1. 回归树特点

解决回归问题的决策树模型
必须是二叉树结构
节点分裂依据是使均方误差（MSE）最小化

2. 回归树计算示例

以简单数据集为例：

x	1	2	3	4	5	6	7	8	9	10
y	5.56	5.7	5.91	6.4	6.8	7.05	8.9	8.7	9	9.05

通过计算不同切分点的损失函数，找到最优切分点，逐步构建回归树。

损失函数 ：
L ( j , s ) = ∑ x i ∈ R 1 ( j , s ) ( y i − c ^ 1 ) 2 + ∑ x i ∈ R 2 ( j , s ) ( y i − c ^ 2 ) 2 L(j, s) = \sum_{x_i \in R_1(j, s)} (y_i - \hat{c}1)^2 + \sum{x_i \in R_2(j, s)} (y_i - \hat{c}_2)^2 L(j,s)=∑xi∈R1(j,s)(yi−c^1)2+∑xi∈R2(j,s)(yi−c^2)2

其中 c ^ 1 \hat{c}_1 c^1和 c ^ 2 \hat{c}_2 c^2 分别是两个区域的样本均值。

四、Scikit-learn中的决策树实现

1. 分类决策树参数

python 复制代码

from sklearn.tree import DecisionTreeClassifier

主要参数说明：

criterion: 分裂标准，'gini'（基尼系数）或 'entropy'（信息熵）
max_depth: 树的最大深度，防止过拟合
min_samples_split: 分裂内部节点所需的最小样本数
min_samples_leaf: 叶子节点最少样本数
max_leaf_nodes: 最大叶子节点数
random_state: 随机种子，保证结果可重复

2. 回归决策树参数

python 复制代码

from sklearn.tree import DecisionTreeRegressor

主要参数说明：

criterion: 分裂标准，'mse'（均方误差）或 'mae'（平均绝对误差）
其他参数与分类树类似

五、Python实现示例

1. 分类决策树实现

python 复制代码

import pandas as pd
from sklearn import tree
from sklearn.model_selection import train_test_split
from sklearn import metrics
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix

# 可视化混淆矩阵函数
def cm_plot(y, yp):
    cm = confusion_matrix(y, yp)
    plt.matshow(cm, cmap=plt.cm.Blues)
    plt.colorbar()
    for x in range(len(cm)):
        for y_ in range(len(cm)):
            plt.annotate(cm[x, y_], xy=(y_, x), horizontalalignment='center',
                         verticalalignment='center')
    plt.ylabel('True label')
    plt.xlabel('Predicted label')
    return plt

# 导入数据
datas = pd.read_excel("电信客户流失数据.xlsx")

# 划分特征和标签
data = datas.iloc[:, :-1]
target = datas.iloc[:, -1] 

# 划分训练集和测试集
data_train, data_test, target_train, target_test = \
    train_test_split(data, target, test_size=0.2, random_state=42)

# 创建决策树分类器
dtr = tree.DecisionTreeClassifier(criterion='gini', max_depth=5, random_state=60)

# 训练模型
dtr.fit(data_train, target_train)

# 训练集预测
train_predicted = dtr.predict(data_train)

# 评估训练集
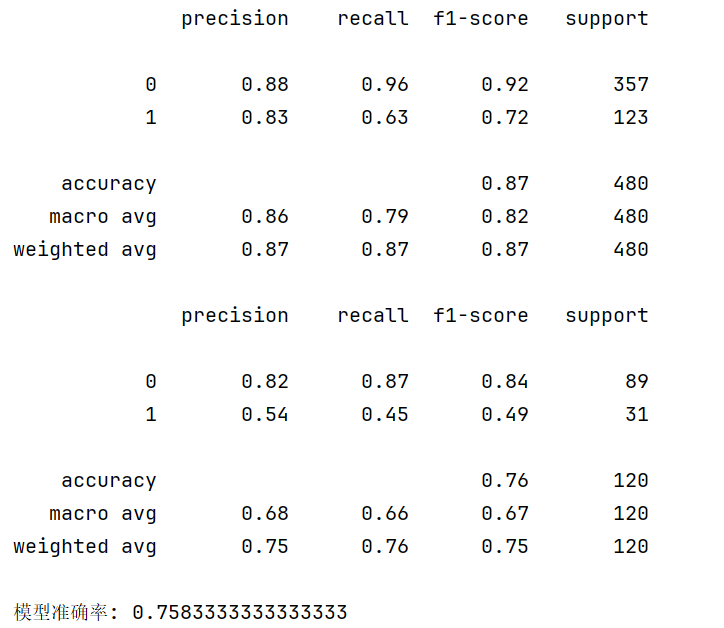
print(metrics.classification_report(target_train, train_predicted))
cm_plot(target_train, train_predicted).show()

# 测试集预测
test_predicted = dtr.predict(data_test)

# 评估测试集
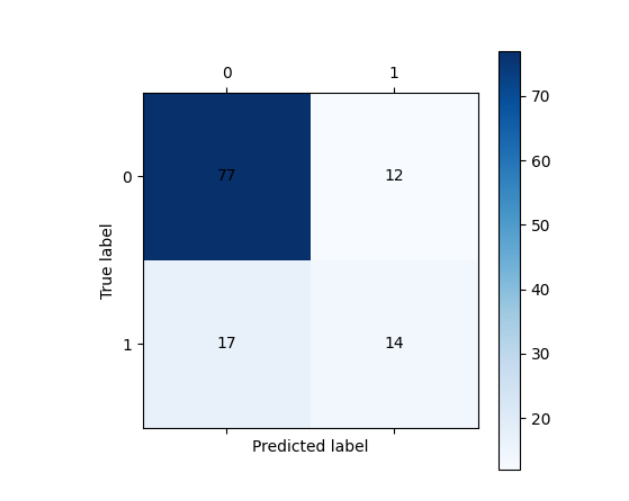
print(metrics.classification_report(target_test, test_predicted))
cm_plot(target_test, test_predicted).show()

# 模型评分
score = dtr.score(data_test, target_test)
print(f"模型准确率: {score}")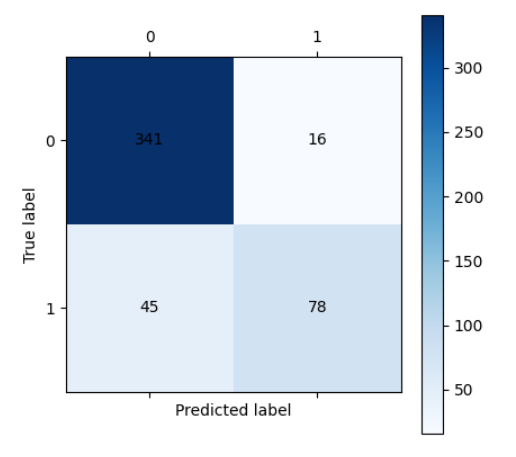

六、决策树剪枝

1. 剪枝的目的

防止过拟合，提高模型泛化能力。

2. 剪枝方法

预剪枝 ：在树构建过程中提前停止生长
- 限制树的深度
- 限制叶子节点的个数
- 限制叶子节点的样本数
后剪枝：先构建完整的树，然后自底向上进行剪枝

3. 预剪枝策略

限制树的深度（max_depth）
限制叶子节点的个数（max_leaf_nodes）
限制分裂节点的最小样本数（min_samples_split）
限制叶子节点的最小样本数（min_samples_leaf）

七、模型评估指标

1. AUC-ROC曲线

AUC：曲线下面积，衡量模型对正负样本的区分能力
ROC：接收者操作特征曲线，显示不同阈值下真正例率和假正例率的关系

2. AUC的优点

考虑了分类器对正例和负例的分类能力
在样本不平衡的情况下依然有效
不受样本不平衡问题影响，是相对稳健的评价指标

python 复制代码

# AUC值计算
y_pred_proba = dtr.predict_proba(data_test)
a = y_pred_proba[:, 1]
auc_result = metrics.roc_auc_score(target_test, a)
print(f"AUC值: {auc_result}")

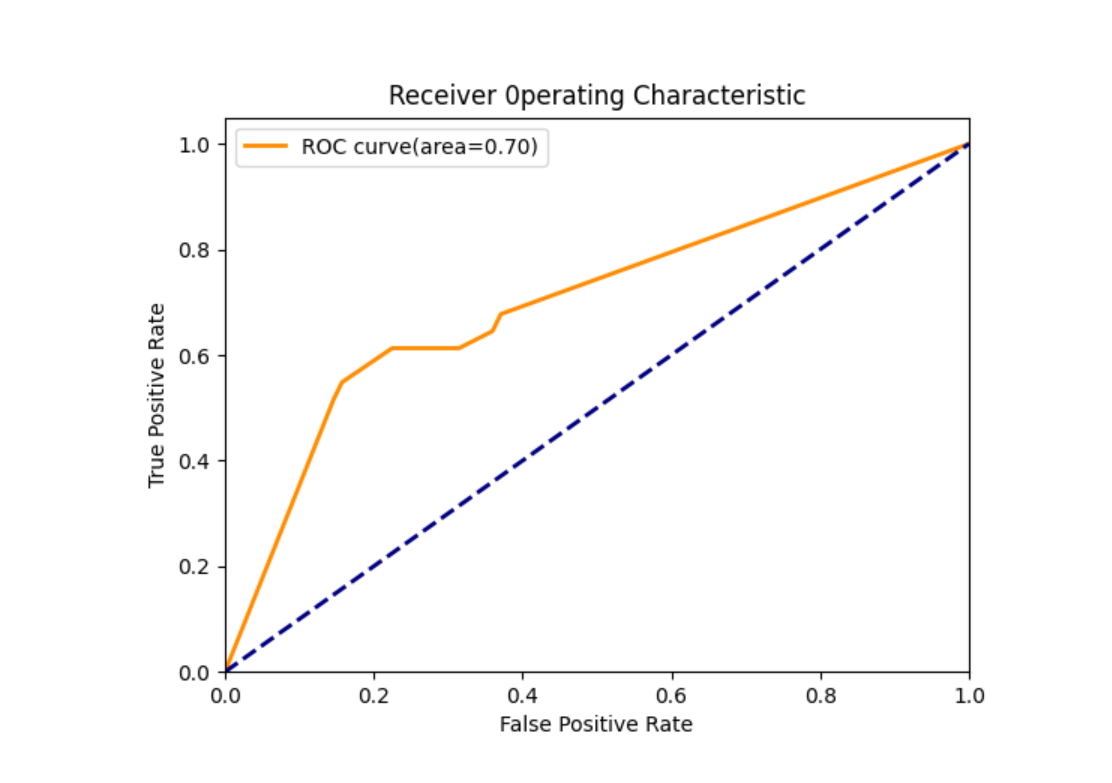
# 绘制ROC曲线
from sklearn.metrics import roc_curve

fpr, tpr, thresholds = roc_curve(target_test, a)

plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (area={auc_result:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend()
plt.show()