《Java数据结构与算法》第四篇（三）二叉树遍历详解_CSDN文章

一起养小猫2025-12-19 9:45

Java数据结构之树：二叉树的三种遍历方法详解（递归与非递归实现）

目录

一、二叉树遍历的定义与重要性

二叉树遍历（Binary Tree Traversal）是指按照某种顺序访问二叉树中的所有节点，使得每个节点都被访问一次且仅一次。遍历是二叉树最基本、最重要的操作，是后续进行二叉树搜索、修改、删除等操作的基础。

根据访问节点的顺序不同，二叉树的遍历主要分为三种方式：

  1. 前序遍历（Preorder Traversal）：根节点 → 左子树 → 右子树
  2. 中序遍历（Inorder Traversal）：左子树 → 根节点 → 右子树
  3. 后序遍历（Postorder Traversal）：左子树 → 右子树 → 根节点

每种遍历方式都有递归和非递归两种实现方法。递归实现简洁易懂，而非递归实现通过使用栈（Stack）数据结构来模拟递归过程，空间效率更高。

二、前序遍历（DLR）详解

2.1 前序遍历的定义

前序遍历（DLR，Data-Left-Right）是二叉树遍历中最直观的方式。其遍历规则为：

  1. 首先访问根节点
  2. 然后遍历左子树
  3. 最后遍历右子树

对于测试用例 ABD##E##C## 构建的二叉树：

复制代码 
    A
   / \
  B   C
 / \
D   E

前序遍历的结果为：A B D E C

2.2 递归实现
java 复制代码 
public void DLR(BiTreeNode root) {
    if (root != null) {
        System.out.print(root.data + " ");  // 访问根节点
        DLR(root.lchild);                   // 遍历左子树
        DLR(root.rchild);                   // 遍历右子树
    }
}

代码分析：

  • 递归实现非常简洁，只有三行核心代码
  • 时间复杂度：O(n)，每个节点访问一次
  • 空间复杂度：O(h)，h为树的高度，递归调用栈的深度
2.3 非递归实现（数组模拟栈）
java 复制代码 
public void DLR2() {
    BiTreeNode stack[] = new BiTreeNode[20];  // 使用数组模拟栈
    int top = 0;
    BiTreeNode curr = root;

    while (curr != null || top > 0) {
        if (curr != null) {
            System.out.print(curr.data + " ");  // 访问当前节点
            stack[top++] = curr;                // 当前节点入栈
            curr = curr.lchild;                 // 转向左子树
        }
        if (top > 0) {
            curr = stack[--top];                // 出栈
            curr = curr.rchild;                 // 转向右子树
        }
    }
}
2.4 非递归实现（Java Stack类）
java 复制代码 
public String DLR3() {
    StringBuilder result = new StringBuilder();
    if (root == null) {
        return "";
    }

    Stack<BiTreeNode> stack = new Stack<>();
    stack.push(root);  // 根节点入栈

    while (!stack.isEmpty()) {
        BiTreeNode curr = stack.pop();
        result.append(curr.data + " ");  // 访问当前节点

        // 右子树先入栈（后处理）
        if (curr.rchild != null) {
            stack.push(curr.rchild);
        }
        // 左子树后入栈（先处理）
        if (curr.lchild != null) {
            stack.push(curr.lchild);
        }
    }
    return result.toString();
}

注意：这里右子树先入栈，左子树后入栈，因为栈是后进先出（LIFO）的数据结构，这样才能保证先处理左子树。

三、中序遍历（LDR）详解

3.1 中序遍历的定义

中序遍历（LDR，Left-Data-Right）的特点是：

  1. 首先遍历左子树
  2. 然后访问根节点
  3. 最后遍历右子树

对于同一棵二叉树，中序遍历的结果为：D B E A C

重要特性：对于二叉搜索树（BST），中序遍历会得到有序的节点序列。

3.2 递归实现
java 复制代码 
public void LDR(BiTreeNode root) {
    if (root != null) {
        LDR(root.lchild);                   // 先遍历左子树
        System.out.print(root.data);        // 再访问根节点
        LDR(root.rchild);                   // 最后遍历右子树
    }
}
3.3 非递归实现
java 复制代码 
public String LDR2() {
    StringBuilder result = new StringBuilder();
    if (root == null) {
        return "";
    }

    Stack<BiTreeNode> stack = new Stack<>();
    BiTreeNode curr = root;

    while (!stack.isEmpty() || curr != null) {
        // 一直向左走到底
        while (curr != null) {
            stack.push(curr);
            curr = curr.lchild;
        }

        // 弹出栈顶节点并访问
        curr = stack.pop();
        result.append(curr.data + " ");

        // 转向右子树
        curr = curr.rchild;
    }
    return result.toString();
}

算法思路：

  1. 从根节点开始，将路径上的所有节点入栈，直到最左边的叶子节点
  2. 弹出栈顶节点并访问
  3. 转向该节点的右子树，重复上述过程

四、后序遍历（LRD）详解

4.1 后序遍历的定义

后序遍历（LRD，Left-Right-Data）的顺序为：

  1. 首先遍历左子树
  2. 然后遍历右子树
  3. 最后访问根节点

对于同一棵二叉树，后序遍历的结果为：D E B C A

应用场景：后序遍历常用于需要先处理子节点再处理父节点的场景，如计算目录大小、释放树形结构内存等。

4.2 递归实现
java 复制代码 
public void LRD(BiTreeNode root) {
    if (root != null) {
        LRD(root.lchild);                   // 先遍历左子树
        LRD(root.rchild);                   // 再遍历右子树
        System.out.print(root.data);        // 最后访问根节点
    }
}
4.3 非递归实现（双栈法）
java 复制代码 
public String LRD2() {
    StringBuilder result = new StringBuilder();
    if (root == null) {
        return "";
    }

    Stack<BiTreeNode> stack1 = new Stack<>();  // 辅助栈
    Stack<BiTreeNode> stack2 = new Stack<>();  // 结果栈
    stack1.push(root);

    while (!stack1.isEmpty()) {
        BiTreeNode curr = stack1.pop();
        stack2.push(curr);  // 将节点放入结果栈

        // 左子树先入栈
        if (curr.lchild != null) {
            stack1.push(curr.lchild);
        }
        // 右子树后入栈
        if (curr.rchild != null) {
            stack1.push(curr.rchild);
        }
    }

    // 从结果栈中弹出得到后序序列
    while (!stack2.isEmpty()) {
        BiTreeNode curr = stack2.pop();
        result.append(curr.data + " ");
    }
    return result.toString();
}
4.4 非递归实现（单栈法）
java 复制代码 
public String LRD3() {
    StringBuilder result = new StringBuilder();
    if (root == null) {
        return "";
    }

    Stack<BiTreeNode> stack = new Stack<>();
    BiTreeNode curr = root;
    BiTreeNode prev = null;  // 记录上一个访问的节点

    while (!stack.isEmpty() || curr != null) {
        if (curr != null) {
            stack.push(curr);
            curr = curr.lchild;
        } else {
            BiTreeNode temp = stack.peek();
            // 如果右子树存在且未被访问
            if (temp.rchild != null && prev != temp.rchild) {
                curr = temp.rchild;
            } else {
                // 访问该节点
                result.append(temp.data + " ");
                prev = stack.pop();
            }
        }
    }
    return result.toString();
}

五、完整代码实现与测试

5.1 二叉树节点类
java 复制代码 
class BiTreeNode {
    char data;                    // 节点数据
    BiTreeNode lchild, rchild;    // 左右孩子指针

    // 默认构造函数
    public BiTreeNode() {
    }

    // 带参数的构造函数
    public BiTreeNode(char data) {
        this.data = data;
        lchild = null;
        rchild = null;
    }

    // 完整构造函数
    public BiTreeNode(char data, BiTreeNode lchild, BiTreeNode rchild) {
        this.data = data;
        this.lchild = lchild;
        this.rchild = rchild;
    }
}
5.2 二叉树的构建
java 复制代码 
public void createBiTree(String input) {
    pi = 0;
    root = createBiTreeHelper(input);
    num = countNodes(root);
}

private BiTreeNode createBiTreeHelper(String input) {
    if (pi >= input.length() || input.charAt(pi) == '#') {
        pi++;
        return null;  // #表示空节点
    }

    BiTreeNode root = new BiTreeNode(input.charAt(pi));
    ++pi;
    root.lchild = createBiTreeHelper(input);  // 递归构建左子树
    root.rchild = createBiTreeHelper(input);  // 递归构建右子树
    return root;
}

构建规则 ：使用先序序列和特殊字符#来表示空节点，如ABD##E##C##。

5.3 运行结果测试

运行截图展示了三种遍历方式的测试结果：

测试用例构建的二叉树结构：

复制代码 
     A
    / \
   B   C
  / \
 D   E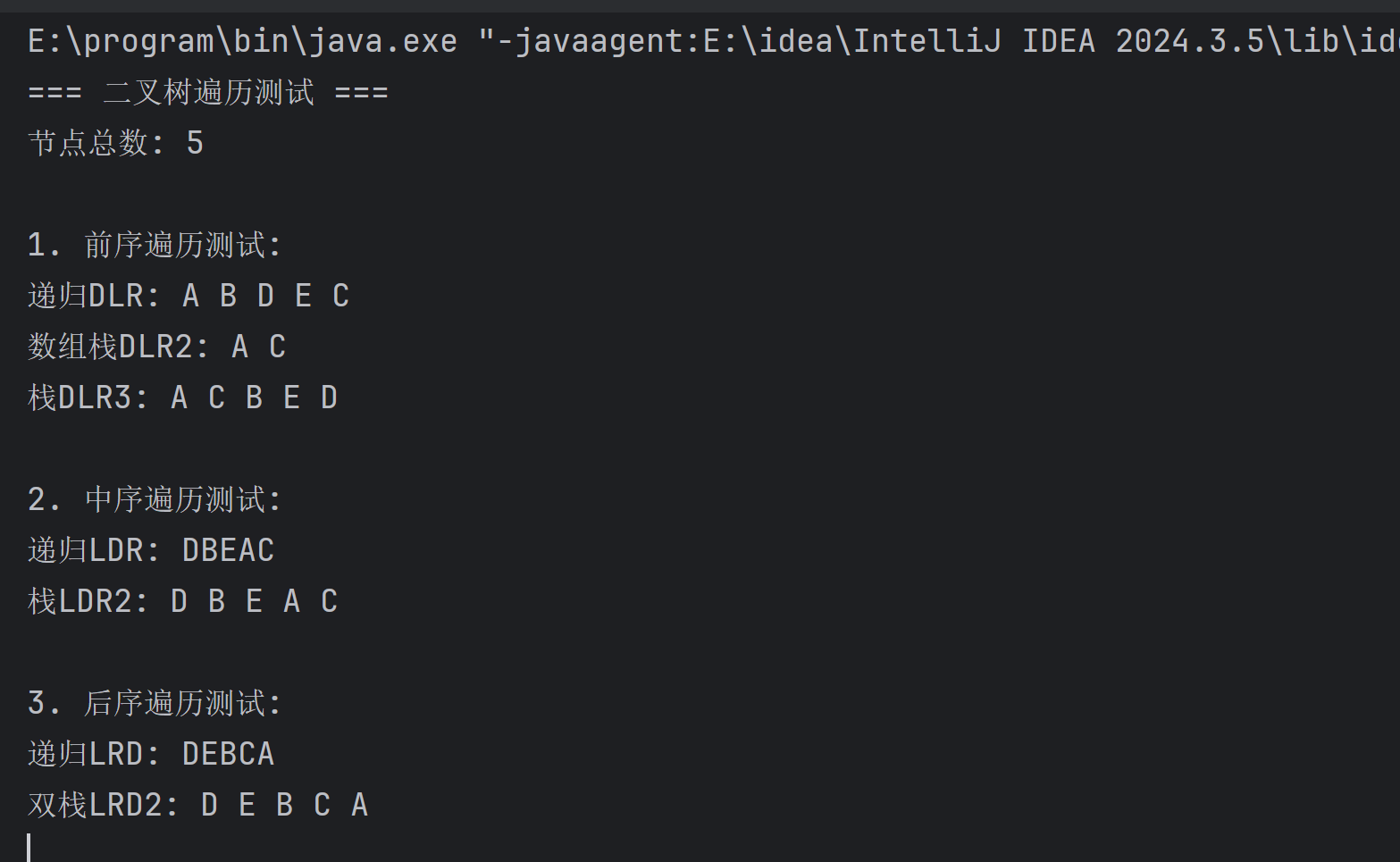

六、性能对比与应用场景

6.1 时间空间复杂度对比
遍历方法 时间复杂度 空间复杂度（递归） 空间复杂度（非递归）
前序遍历 O(n) O(h) O(h)
中序遍历 O(n) O(h) O(h)
后序遍历 O(n) O(h) O(h)

其中n为节点数，h为树的高度。最坏情况下（树退化为链表），h = n。

6.2 非递归实现的优势
  1. 空间效率更高：避免了递归调用的开销
  2. 不会栈溢出：递归深度过深时可能导致栈溢出
  3. 更好的控制：可以在遍历过程中进行更灵活的操作
6.3 应用场景
  • 前序遍历：复制树结构、表达式树求值
  • 中序遍历：二叉搜索树的中序输出（有序序列）
  • 后序遍历：计算表达式值、释放树内存、文件系统遍历

七、总结与学习建议

7.1 核心要点总结
  1. 理解遍历本质：二叉树遍历是将树形结构线性化的过程
  2. 掌握递归思想：递归实现简洁直观，是理解遍历的基础
  3. 理解栈的作用：非递归实现通过栈模拟递归调用过程
  4. 注意特殊情况：空树、单节点树等边界条件
  5. 选择合适方法：根据实际需求选择递归或非递归实现
7.2 学习建议
  1. 画图辅助理解：手动画出遍历路径，加深理解
  2. 调试跟踪过程：使用IDE调试功能跟踪遍历过程
  3. 多种实现方式：掌握同一遍历的不同实现方法
  4. 实际应用练习：结合实际问题练习遍历应用
7.3 扩展学习

二叉树遍历是树形结构的基础，建议继续学习：

  • 层次遍历（广度优先搜索）
  • 线索二叉树
  • 平衡二叉树（AVL树）
  • 红黑树
  • B树和B+树

参考资源：

标签： #Java数据结构 #二叉树 #树遍历 #算法实现 #数据结构基础

如果这篇文章对你有帮助，欢迎点赞、收藏和评论！有疑问的小伙伴可以在评论区留言交流。

相关推荐
im_AMBER2 小时前
Leetcode 80 统计一个数组中好对子的数目
数据结构·c++·笔记·学习·算法·leetcode
少许极端2 小时前
算法奇妙屋(十九)-子序列问题(动态规划)
java·数据结构·算法·动态规划·子序列问题
小满、2 小时前
RabbitMQ：AMQP 原理、Spring AMQP 实战与 Work Queue 模型
java·rabbitmq·java-rabbitmq·spring amqp·amqp 协议·work queue
萧曵 丶2 小时前
Java Stream 实际用法详解
java·stream·lambda
消失的旧时光-19432 小时前
从 Android 回调到 C 接口：函数指针 + void* self 的一次彻底理解
android·c语言·开发语言
dvlinker2 小时前
动态代理技术实战测评—高效解锁Zillow房价历史
android·java·数据库
喵手2 小时前
JVM 基础知识：深入理解 Java 的运行时环境！
java·jvm·jvm基础·java运行环境
我命由我123452 小时前
Python Flask 开发问题：ImportError: cannot import name ‘escape‘ from ‘flask‘
服务器·开发语言·后端·python·flask·学习方法·python3.11
简烦2 小时前
外层事务的 afterCommit 中调用内层事务方法时，内层事务的 TransactionSynchronization 注册失败 / 不执行
java·spring
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）05BongoCat - 跨平台键盘猫动画工具06安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）07【AutoGLM部署】本地私有化部署AI手机Agent08Neo4j（一） - Neo4j安装教程（Windows）09Open-AutoGLM Windows 安装部署教程10Cursor 又偷偷更新，这个功能太实用：Visual Editor for Cursor Browser