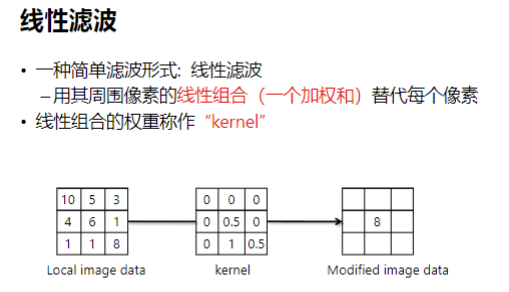
滤波后:图像的像素是原始像素的组合
为什么这么做?
- 增强图像
- 例:移除噪点
- 例:锐化和增强图像
- 从图像中得到有用信息
- 例:提取轮廓或边界 (有助于理解形状)
关于滤波可以做到这些的解释(from Gemini3)
核心逻辑在于:利用图像中像素与周围像素的关系(空间相关性)。
之所以能做到你列出的这些(去噪、锐化、提取轮廓),是因为图像在数学本质 上是一个矩阵。我们通过一种叫做"卷积"(Convolution)的运算,用一个小矩阵(滤波器/核)去和图像矩阵做运算,从而改变像素的值。
这里的核心秘密在于:你想保留什么频率的信息?
1. 为什么能"移除噪点"?(平滑 / Smoothing)
核心原理: "少数服从多数" (平均化 / 积分)
- 现象: 噪点通常表现为像素值的突然跳变(比如一片黑色背景中突然出现一个白点)。这是一个高频信号。
- 怎么做: 我们使用一个低通滤波器(比如均值滤波器或高斯滤波器)。
- 数学逻辑:
- 想象一个 3×33\times33×3 的方框扫过图像。它把方框内 9 个像素的值加起来取平均值,然后用这个平均值替代中心像素。
- 因为噪点是孤立的,周围的正常像素占大多数。
- 一平均,噪点的极端值就被"拉平"了,融入了背景。
- 代价: 图像变模糊了(因为边缘也被"平均"掉了)。
2. 为什么能"提取轮廓或边界"?
核心原理: "寻找差异" (求导 / 微分)
- 现象: 什么是轮廓?轮廓就是颜色剧烈变化的地方(比如从白色的桌子到黑色的背景)。这种剧烈变化在数学上叫**梯度(Gradient)**大。
- 怎么做: 我们使用一个高通滤波器(比如 Sobel 算子或 Canny 算子)。
- 数学逻辑:
- 这类滤波器通常是一边正数、一边负数(例如左边是 -1,右边是 +1)。
- 如果在平坦区域(颜色一样),100×(−1)+100×1=0100 \times (-1) + 100 \times 1 = 0100×(−1)+100×1=0。结果是黑色。
- 如果在边缘区域(左黑右白),0×(−1)+255×1=2550 \times (-1) + 255 \times 1 = 2550×(−1)+255×1=255。结果是白色(亮线)。
- 这样,只有变化剧烈的地方被保留了下来,平坦的地方都变成了黑色。
3. 为什么能"锐化和增强图像"?
核心原理: "原图 + 轮廓"
- 现象: 图像看起来模糊,是因为边缘不够"陡峭",过渡太温和。
- 怎么做: 锐化其实是上述两种操作的结合。
- 数学逻辑:
- 锐化后的图像=原图+(原图−平滑后的图) 锐化后的图像 = 原图 + (原图 - 平滑后的图) 锐化后的图像=原图+(原图−平滑后的图)
- 或者更简单理解:
- 锐化后的图像=原图+边缘(高频细节) 锐化后的图像 = 原图 + 边缘(高频细节)锐化后的图像=原图+边缘(高频细节)
- 我们先把边缘(轮廓)提取出来,然后把这个边缘叠加回原图上,让边界的黑更黑、白更白,人眼看起来就觉得图像变"清晰"了。
总结:一切都在于"邻居"
你之所以能对图像做这些操作,是因为你不仅仅看一个像素本身,而是看它和它邻居的数学关系:
- 想去噪? 让像素变得像它的邻居(模糊/求平均)。
- 想找轮廓? 找像素不像它邻居的地方(求差异/求导数)。
- 想锐化? 放大像素与邻居的差异。
卷积与互相关

所谓两个函数的卷积,本质上就是先将一个函数翻转,然后进行滑动叠加。
卷积实际上就是互相关的翻转