【计算机视觉】02_边缘

边缘介绍

定义

边缘是图像强度函数中变化迅速的地方。

• 从 3D 视角 来看，边缘在强度函数曲面上看起来像陡峭的悬崖。
• 从 1D 扫描线 来看，边缘对应于强度函数的一阶导数中的极值。

表示形式

基于边缘的图像分割方法建立在边缘像素灰度值会出现阶跃或屋顶型变化的观察现象上。

• 阶跃型边缘： 强度值突然从一个水平跳到另一个水平（例如黑到白）。
• 屋顶型边缘： 强度值先平滑上升到峰值，再平滑下降（例如细线）。

边缘检测

A. 图像导数与梯度

要检测数字图像 Fx,yFx, yFx,y 的变化，我们可以采取**离散导数（有限差分）**的方法。

• 一阶导数（梯度）： 边缘对应于一阶导数的极值点 ；梯度指向强度增加最快的方向。
• 二阶导数： 边缘对应于二阶导数的过零点（零交叉点）。

图像梯度是图像变化的关键度量：

• 边缘强度由梯度的大小给出。
• 梯度方向 可以通过 θ=atan2⁡(gy,gx)\theta = \operatorname{atan2}(g_y, g_x)θ=atan2(gy,gx) 给出。

噪声的影响

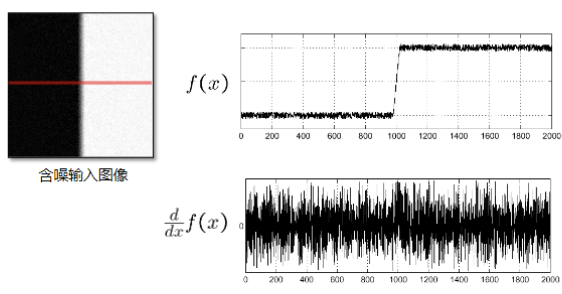
噪声让我们无法通过导数来判断边缘在哪里

解决方法

先进行平滑处理

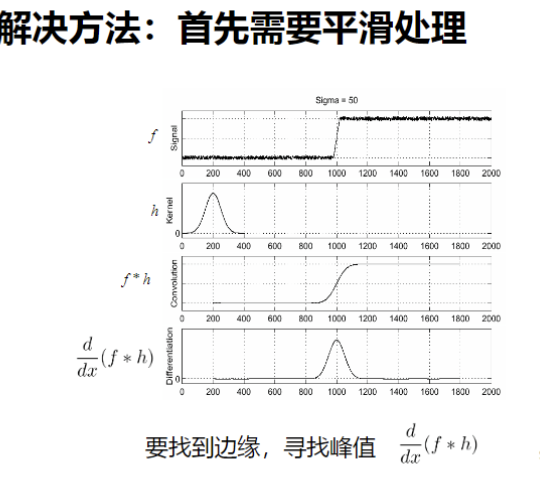
这里的 hhh就是kernel，也就是滤波器，这里是高斯函数（正态分布），代表权重 ，当它滑动过信号时，它在说："我最相信中间的像素，但旁边的像素我也听一点意见，大家一起取个加权平均值。"

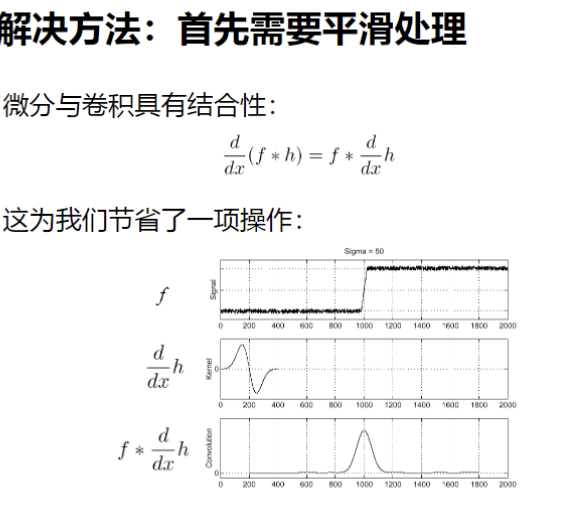
我们要找边缘，但噪声太烦人，所以我们先用高斯函数 把图像罩住磨平一下。第二张图告诉我们，与其分两步走，不如直接做一个自带求导功能的平滑刷子（DoG算子），刷一下就直接出结果。

Canny算子

1. 降噪（使用高斯滤波）

2. 计算梯度幅值和方向

   • 做法： 通常使用 Sobel 算子（分别在 x 方向和 y 方向做卷积）。

     • GxG_xGx: 水平方向的变化。

     • GyG_yGy: 垂直方向的变化。

   • 计算两个关键值：

     1. 梯度的强度 (Edge Strength): G=Gx2+Gy2G = \sqrt{G_x^2 + G_y^2}G=Gx2+Gy2 （也就是斜坡有多陡）。

     2. 梯度的方向 (Edge Direction): θ=arctan⁡(Gy/Gx)\theta = \arctan(G_y / G_x)θ=arctan(Gy/Gx) （也就是斜坡朝哪边倾斜）。

3. 非极大值抑制

   • 直观理解： 想象你在爬一座山脊（边缘）。我们要找的是山脊最高的那条线（山棱）。

   • 规则：

     1. 沿着梯度的方向看（也就是垂直于边缘的方向）。

     2. 如果当前像素的梯度值比它前方 和后方的像素都要大，那么它就是"山顶"，保留它。

     3. 如果它比旁边的小，说明它只是山坡的一部分，不是最高点，把它置为 0（抑制）。

   • 结果： 原本宽宽的边缘，瞬间变成了细细的一条线。

4. 双阈值与之后边界跟踪

   1. 2个阈值，3种情形
   2. R > T: 强边缘
   3. R < T 但 R > t： 弱边缘
   4. R < t：无边缘

算子性能

Canny 算子的性能取决于几个参数 ，其中一个关键参数是 σ\sigmaσ：高斯模糊的宽度。

• σ\sigmaσ 的选择取决于预期的目标。
• σ\sigmaσ 大 ：检测大尺度边缘。
• σ\sigmaσ 小 ：检测精细边缘。

在尺度空间 的属性中，随着尺度 (σ\sigmaσ) 的增加：边缘位置可能会移动，两条边可能会合并，但一条边不会一分为二 。