在MATLAB中实现用于控制、优化等自动化领域的模糊神经网络,核心是利用ANFIS(自适应神经模糊推理系统)。它完美结合了模糊逻辑的知识表达能力和神经网络的学习能力。
下图展示其工作原理和实现流程:
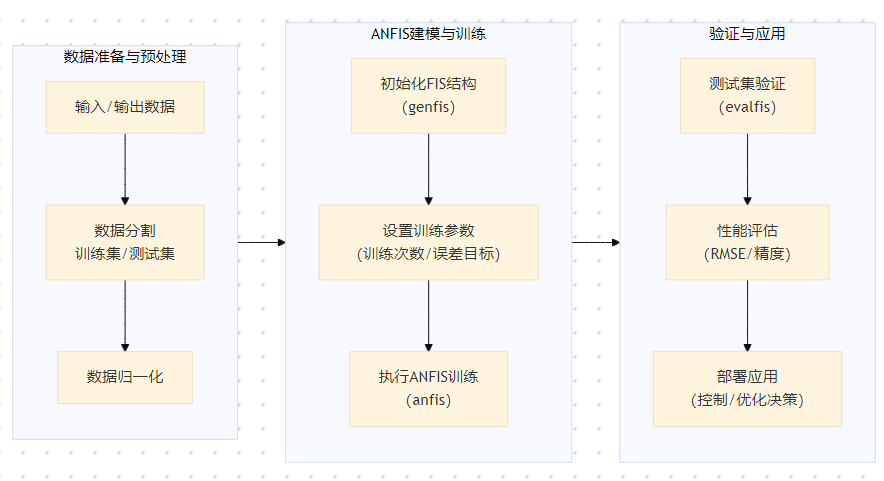
MATLAB 实现步骤与代码
在MATLAB中构建和训练一个ANFIS模型的详细步骤和示例代码。以一个经典的函数逼近问题为例:根据输入x预测输出y。
matlab
%% 1. 准备训练数据(示例:非线性函数)
% 假设系统有两个输入 x1, x2 和一个输出 y
x1 = linspace(-10, 10, 100)';
x2 = linspace(-10, 10, 100)';
% 生成一个非线性函数的输出作为目标(可替换为您的实际数据)
y = 5 * sin(x1) + cos(x2) .* x1;
% 组合输入数据
data = [x1, x2, y];
% 划分训练集和测试集(例如80%训练,20%测试)
train_ratio = 0.8;
num_samples = size(data, 1);
num_train = round(train_ratio * num_samples);
train_data = data(1:num_train, :);
test_data = data(num_train+1:end, :);
%% 2. 生成初始模糊推理系统(FIS)
% 使用 genfis 函数生成初始FIS结构。这里使用网格分割法。
num_mf = [3 5]; % 为每个输入分别指定隶属度函数的数量(例如x1:3个,x2:5个)
mf_type = 'gbellmf'; % 指定隶属度函数类型,如'gbellmf'(广义钟形), 'gaussmf'(高斯型)
init_fis = genfis1(train_data, num_mf, mf_type);
% 可视化初始隶属度函数
figure;
subplot(2,1,1);
plotmf(init_fis, 'input', 1); % 查看第一个输入的初始隶属度函数
title('输入 x1 的初始隶属度函数');
subplot(2,1,2);
plotmf(init_fis, 'input', 2); % 查看第二个输入的初始隶属度函数
title('输入 x2 的初始隶属度函数');
%% 3. 训练ANFIS模型
% 设置训练参数
epoch_n = 100; % 最大训练次数(可调整)
trnOpt = [epoch_n, 0, 0.01, 0.9, 1.1]; % [最大迭代次数, 误差目标, 初始步长, 步长减小率, 步长增加率]
dispOpt = 10; % 每10次迭代显示一次训练信息
% 开始训练
[trn_fis, trainError, stepSize, chkFis, chkError] = anfis(train_data, init_fis, trnOpt, dispOpt, test_data);
% 绘制训练误差曲线
figure;
plot(1:length(trainError), trainError, 'b-', 1:length(chkError), chkError, 'r--');
xlabel('迭代次数');
ylabel('均方根误差(RMSE)');
legend('训练集误差', '测试集误差(防止过拟合)');
title('ANFIS训练误差曲线');
grid on;
%% 4. 使用训练好的ANFIS模型进行预测与验证
% 对测试集进行预测
test_input = test_data(:, 1:2);
predicted_output = evalfis(test_input, trn_fis);
actual_output = test_data(:, 3);
% 计算预测性能指标(例如均方根误差RMSE)
mse = mean((predicted_output - actual_output).^2);
rmse = sqrt(mse);
fprintf('测试集上的均方根误差(RMSE)为: %.4f\n', rmse);
% 绘制预测值与实际值的对比散点图
figure;
plot(actual_output, predicted_output, 'ro');
hold on;
plot([min(actual_output), max(actual_output)], [min(actual_output), max(actual_output)], 'b--');
xlabel('实际输出');
ylabel('ANFIS预测输出');
title(sprintf('预测 vs 实际 (RMSE = %.4f)', rmse));
grid on;
legend('数据点', '理想拟合线', 'Location', 'best');
%% 5. (进阶)将训练好的ANFIS模型部署为Simulink模块
% 如果安装了Simulink,可以将训练好的fis结构导出到工作空间,
% 然后在Simulink库浏览器中找到"Fuzzy Logic Controller"模块进行配置。
% 也可使用命令:fuzzyLogicDesigner(trn_fis) 打开交互式设计器查看和调整。
writeFIS(trn_fis, 'my_trained_anfis_model'); % 保存模型到文件参考代码 模糊神经网络的实现 用于控制,优化等自动领域 www.youwenfan.com/contentcsn/95848.html
ANFIS在自动控制与优化中的核心应用
-
非线性系统建模与控制器设计
- 场景:为复杂的非线性被控对象(如化工反应器、无人机)建立逆模型或直接设计控制器。
- 做法:使用系统输入输出数据训练ANFIS,使其学习输入(状态、误差)到输出(控制量)之间的映射关系。训练好的ANFIS可直接作为控制器。
-
参数优化与系统调参
- 场景:优化控制器(如PID)的参数,或调整生产过程中的关键设定值。
- 做法:以待优化参数为ANFIS输入,以系统性能指标(如超调量、稳态误差、能耗)为输出。通过历史最优数据训练ANFIS,建立"工况/目标 -> 最优参数"的推理系统,用于在线推荐或设置参数。
关键注意事项与技巧
- 数据质量 :数据应尽可能覆盖系统所有典型工况。必要时进行平滑、归一化等预处理。
- 结构选择:输入变量和每个变量的隶属度函数数量不宜过多,以防"维数灾难"和过拟合。可从简单结构开始,逐步增加复杂度。
- 过拟合预防 :务必使用独立的测试集监控训练过程。当测试集误差开始上升而训练集误差仍在下降时,意味着过拟合,应停止训练或简化模型。
- 与PID结合 :一种常见策略是用ANFIS在线整定PID控制器的
Kp,Ki,Kd参数,形成自适应PID控制器。