大模型应用：近似最近邻搜索（ANN）算法驱动向量数据库的高效检索.29

一、引言

在大模型与RAG技术深度融合应用提效增能的场景下，向量数据库成为了连接文本语义化与实时智能检索的关键枢纽。当海量的文本、图像、音频数据被转化为高维向量后，如何在毫秒级时间内从亿级向量库中找到与查询向量最相似的结果，成为了决定上层应用体验的核心瓶颈。

传统的精确最近邻搜索（Brute-force）看似精准，却需要遍历所有向量计算相似度，在数据量达到百万级以上时，耗时会飙升至秒级甚至分钟级，完全无法满足实时应用需求。而近似最近邻搜索（ANN） 算法的出现，打破了这一瓶颈，它以牺牲少量精度为代价，换取指数级的检索速度提升，成为了向量数据库的性能核心。今天我们就深度探索一下传统的精确最近邻搜索和ANN的技术原理，关键特性，以及它与大模型应用的深度绑定关系，深度的理解向量数据库高效检索的底层逻辑。

二、精确最近邻搜索（Brute-force）

1. 基础概念

精确最近邻搜索，Brute-force，也叫暴力搜索，是在高维向量空间中，通过遍历所有向量并逐一计算与查询向量的相似度，即距离，最终筛选出距离最近的 Top-K 向量的检索方法。其核心特点是：无近似、无索引、全量计算，能 100% 返回真实的最近邻结果，是所有近似最近邻（ANN）算法的精度基准。

2. 核心逻辑

对于包含 n 个 d 维向量的数据集 V = {v₁, v₂, ..., vₙ} 和查询向量 q，BF 的执行逻辑为：

• 1. 遍历数据集每个向量 vᵢ ∈ V；
• 2. 计算 q 与 vᵢ的距离（常用余弦距离、欧氏距离）；
• 3. 将所有距离排序，取最小的 Top-K 个距离对应的向量，即为精确最近邻结果。

3. 关键特性

• **精度：**100% 精确，无漏检、无错检
• **时间复杂度：**O (n×d)（n = 向量数量，d = 向量维度），与向量数量/维度线性相关
• **空间复杂度：**O (n×d)，仅需存储原始向量，无需额外索引空间
• **适用场景：**小数据量（万级以下）、精度要求 100% 的场景（如算法对比、小规模实验）
• **缺点：**数据量/维度提升时，计算耗时呈线性爆炸，无法满足实时检索需求

4. 常用距离计算方式

精确最近邻搜索的核心是"距离计算"，两种最常用的距离公式：

4.1 欧氏距离（Euclidean Distance）

• 定义：衡量向量在空间中的直线距离
• 公式：d_euclidean(q, v_i) = √[ Σ(q_k - v_ik)² ]
• 其中：
  • k = 1 到 d，d 是向量维度
  • q_k 和 v_ik 分别表示查询向量 q 和第 i 个向量 v_i 在第 k 维的值
  • Σ 表示对所有维度求和
• 直观理解：计算两个向量各维度差值的平方和，然后取平方根

4.2 余弦距离（Cosine Distance）

• 定义：衡量向量方向的相似度（更适用于嵌入向量）
• 公式：d_cosine(q, v_i) = 1 - [ (q·v_i) / (||q|| × ||v_i||) ]
• 其中：
  • q·v_i 表示两个向量的点积（内积）
  • ||q|| 和 ||v_i|| 分别表示两个向量的模长（范数）
  • 分母是两向量模长的乘积
  • 1 减去余弦相似度得到余弦距离
• 直观理解：
  • 分子 (q·v_i)：衡量两个向量的方向一致性
  • 分母 (||q|| × ||v_i||)：消除向量长度的影响
  • 结果：值越小表示两个向量方向越接近

5. 示例推导

5.1 数据集定义

为便于理解和可视化，选择 2 维向量场景：

• 数据集 V（10 个 2 维随机向量）：
  V = {(1.2, 3.1), (2.5, 4.2), (4.3, 1.8), (5.6, 3.9), (7.2, 2.5), (3.8, 5.4), (6.1, 4.8), (2.9, 1.5), (8.0, 3.2), (0.9, 4.5)}
• 查询向量 q：(5.0, 3.5)
• 检索目标：找到与 q 欧氏距离最近的 Top-3 向量（精确结果）

5.2 BF检索分步执行

第一步：遍历所有向量，计算欧氏距离

• 第1个向量坐标 (1.2, 3.1)，于q的欧式距离：√[(5-1.2)² + (3.5-3.1)²] ≈ 3.82
• 第2个向量坐标 (2.5, 4.2)，于q的欧式距离：√[(5-2.5)² + (3.5-4.2)²] ≈ 2.60
• 第3个向量坐标 (4.3, 1.8)，于q的欧式距离：√[(5-4.3)² + (3.5-1.8)²] ≈ 1.84
• 第4个向量坐标 (5.6, 3.9)，于q的欧式距离：√[(5-5.6)² + (3.5-3.9)²] ≈ 0.72
• 第5个向量坐标 (7.2, 2.5)，于q的欧式距离：√[(5-7.2)² + (3.5-2.5)²] ≈ 2.42
• 第6个向量坐标 (3.8, 5.4)，于q的欧式距离：√[(5-3.8)² + (3.5-5.4)²] ≈ 2.25
• 第7个向量坐标 (6.1, 4.8)，于q的欧式距离：√[(5-6.1)² + (3.5-4.8)²] ≈ 1.70
• 第8个向量坐标 (2.9, 1.5)，于q的欧式距离：√[(5-2.9)² + (3.5-1.5)²] ≈ 2.90
• 第9个向量坐标 (8.0, 3.2)，于q的欧式距离：√[(5-8.0)² + (3.5-3.2)²] ≈ 3.02
• 第10个向量坐标 (0.9, 4.5)，于q的欧式距离：√[(5-0.9)² + (3.5-4.5)²] ≈ 4.22

第二步：按距离升序排序

• 第4个坐标 (5.6, 3.9)，距离值为 0.72
• 第7个坐标 (6.1, 4.8)，距离值为 1.70
• 第3个坐标 (4.3, 1.8)，距离值为 1.84
• 第6个坐标 (3.8, 5.4)，距离值为 2.25
• 第5个坐标 (7.2, 2.5)，距离值为 2.42
• 第2个坐标 (2.5, 4.2)，距离值为 2.60
• 第8个坐标 (2.9, 1.5)，距离值为 2.90
• 第9个坐标 (8.0, 3.2)，距离值为 3.02
• 第1个坐标 (1.2, 3.1)，距离值为 3.82
• 第10个坐标 (0.9, 4.5)，距离值为 4.22

第三步：筛选 Top-3 精确最近邻

• 最终结果：(5.6, 3.9)（距离 0.72）、(6.1, 4.8)（距离 1.70）、(4.3, 1.8)（距离 1.84）

6. 代码示例

6.1 完整代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

# 解决中文显示
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False

# ===================== 1. 数据准备 =====================
np.random.seed(42)  # 固定随机种子，保证结果可复现
# 10个2维随机向量（数据集V）
V = np.array([
    [1.2, 3.1], [2.5, 4.2], [4.3, 1.8], [5.6, 3.9], [7.2, 2.5],
    [3.8, 5.4], [6.1, 4.8], [2.9, 1.5], [8.0, 3.2], [0.9, 4.5]
])
query = np.array([5.0, 3.5])  # 查询向量q
k = 3  # 检索Top-3

# ===================== 2. BF核心计算 =====================
# 计算每个向量与查询向量的欧氏距离
distances = np.linalg.norm(V - query, axis=1)
# 按距离排序，获取Top-K索引
sorted_indices = np.argsort(distances)
top_k_indices = sorted_indices[:k]
top_k_distances = distances[top_k_indices]
top_k_vectors = V[top_k_indices]

# ===================== 3. 动图可视化 =====================
fig, ax = plt.subplots(figsize=(10, 8), tight_layout=True)
ax.set_xlim(0, 9)
ax.set_ylim(1, 6)
ax.set_xlabel('维度1', fontsize=12)
ax.set_ylabel('维度2', fontsize=12)
ax.set_title('精确最近邻搜索（Brute-force）执行过程', fontsize=14)
ax.grid(True, alpha=0.3)

# 初始化绘图元素
# 1. 所有数据集向量（浅灰色）
all_points = ax.scatter(V[:, 0], V[:, 1], c='lightgray', s=60, label='数据集向量')
# 2. 查询向量（红色星号）
query_point = ax.scatter(query[0], query[1], c='red', s=200, marker='*', label='查询向量')
# 3. 遍历中的向量（橙色，动态高亮）
current_point = ax.scatter([], [], c='orange', s=80, edgecolors='black', label='正在计算的向量')
# 4. 距离标注（动态更新）
distance_text = ax.text(0.05, 0.95, '', transform=ax.transAxes, fontsize=10, verticalalignment='top')
# 5. Top-K结果（绿色，逐步显示）
top_k_points = ax.scatter([], [], c='green', s=100, edgecolors='darkgreen', label=f'Top-{k}精确结果')
# 6. 图例
ax.legend(loc='upper right', fontsize=10)

# 初始化动画状态
frames_total = len(V) + k  # 遍历所有向量（10帧） + 显示Top-K（3帧）
current_frame = 0
calculated_indices = []  # 已计算的向量索引
top_k_displayed = 0      # 已显示的Top-K数量

def update(frame):
    global current_frame, calculated_indices, top_k_displayed
    # 阶段1：遍历所有向量，逐点计算距离（前10帧）
    if frame < len(V):
        # 高亮当前计算的向量
        current_point.set_offsets(V[frame].reshape(1, -1))
        # 记录已计算的索引
        calculated_indices.append(frame)
        # 标注当前距离
        dist = distances[frame]
        distance_text.set_text(f'正在计算向量{frame+1}：\n距离 = {dist:.4f}\n已计算{len(calculated_indices)}/{len(V)}个向量')
        # 已计算的向量变浅蓝
        all_points.set_offsets(V)
        all_points.set_color(['lightblue' if i in calculated_indices else 'lightgray' for i in range(len(V))])
    # 阶段2：显示Top-K结果（后3帧）
    elif frame < len(V) + k:
        current_point.set_offsets(np.empty((0, 2)))  # 隐藏当前计算的向量
        distance_text.set_text(f'遍历完成！开始显示Top-{k}精确结果\n已显示{top_k_displayed+1}/{k}个')
        # 逐点显示Top-K结果
        top_k_x = top_k_vectors[:top_k_displayed+1, 0]
        top_k_y = top_k_vectors[:top_k_displayed+1, 1]
        top_k_points.set_offsets(np.c_[top_k_x, top_k_y])
        top_k_displayed += 1
    # 阶段3：完成
    else:
        distance_text.set_text(f'BF检索完成！\nTop-{k}最近邻：\n1. {top_k_vectors[0]}（距离{top_k_distances[0]:.4f}）\n2. {top_k_vectors[1]}（距离{top_k_distances[1]:.4f}）\n3. {top_k_vectors[2]}（距离{top_k_distances[2]:.4f}）')
    
    return all_points, query_point, current_point, distance_text, top_k_points

# 生成动画（保存为GIF）
ani = FuncAnimation(
    fig, update, frames=frames_total, interval=600, blit=True, repeat=False
)
ani.save('brute_force_retrieval.gif', writer='pillow', fps=1.5)
plt.show()

# ===================== 4. 输出结果 =====================
print("===== Brute-force 精确检索结果 =====")
print(f"查询向量：{query}")
print(f"Top-{k}最近邻：")
for i, (vec, dist) in enumerate(zip(top_k_vectors, top_k_distances)):
    print(f"第{i+1}名：向量{vec}，欧氏距离={dist:.4f}")

6.2 代码分析

核心逻辑：

• 用 np.linalg.norm 计算欧氏距离（axis=1 表示按行计算）；
• 用 np.argsort 对距离排序，获取 Top-K 索引；

直观输出展示：

• 分两个阶段：第一阶段（前 10 帧）逐帧高亮遍历的向量，显示实时计算的距离；第二阶段（后 3 帧）逐帧显示 Top-3 精确结果；
• 颜色区分：数据集向量（浅灰→浅蓝）、查询向量（红星）、遍历中向量（橙色）、最终结果（绿色）；
• 文本标注：实时显示计算进度、当前距离、最终结果。

6.3 输出结果

===== Brute-force 精确检索结果 =====

查询向量：[5. 3.5]

Top-3最近邻：

第1名：向量[5.6 3.9]，欧氏距离=0.7211

第2名：向量[6.1 4.8]，欧氏距离=1.7029

第3名：向量[4.3 1.8]，欧氏距离=1.8385

结果图示：

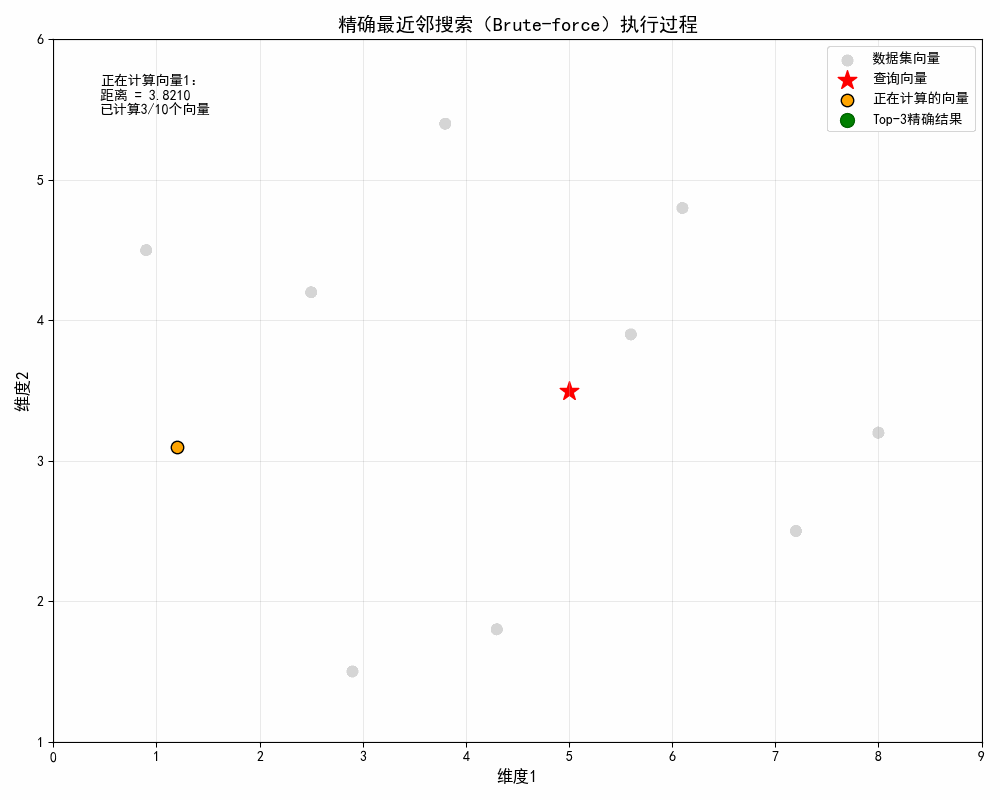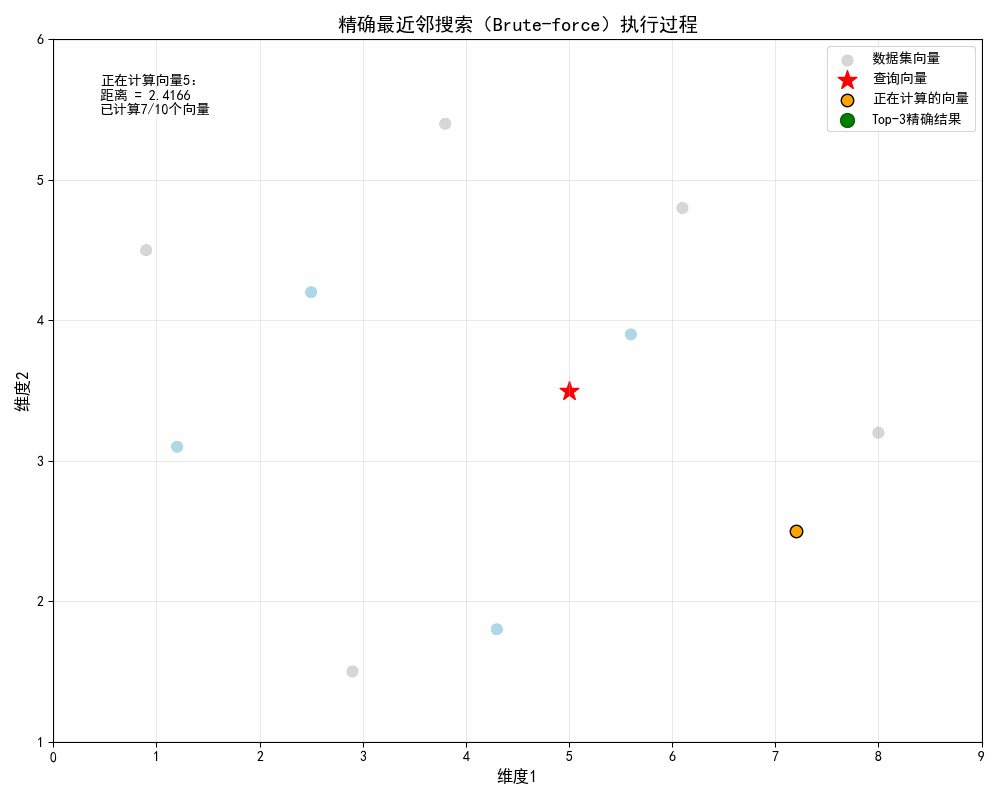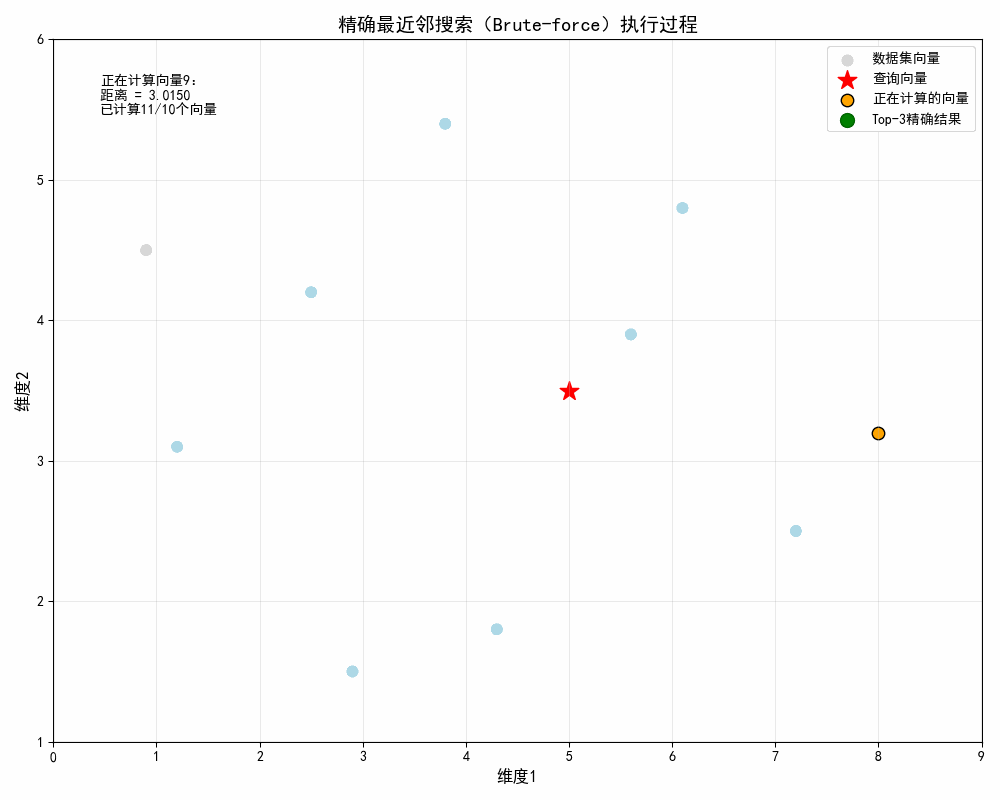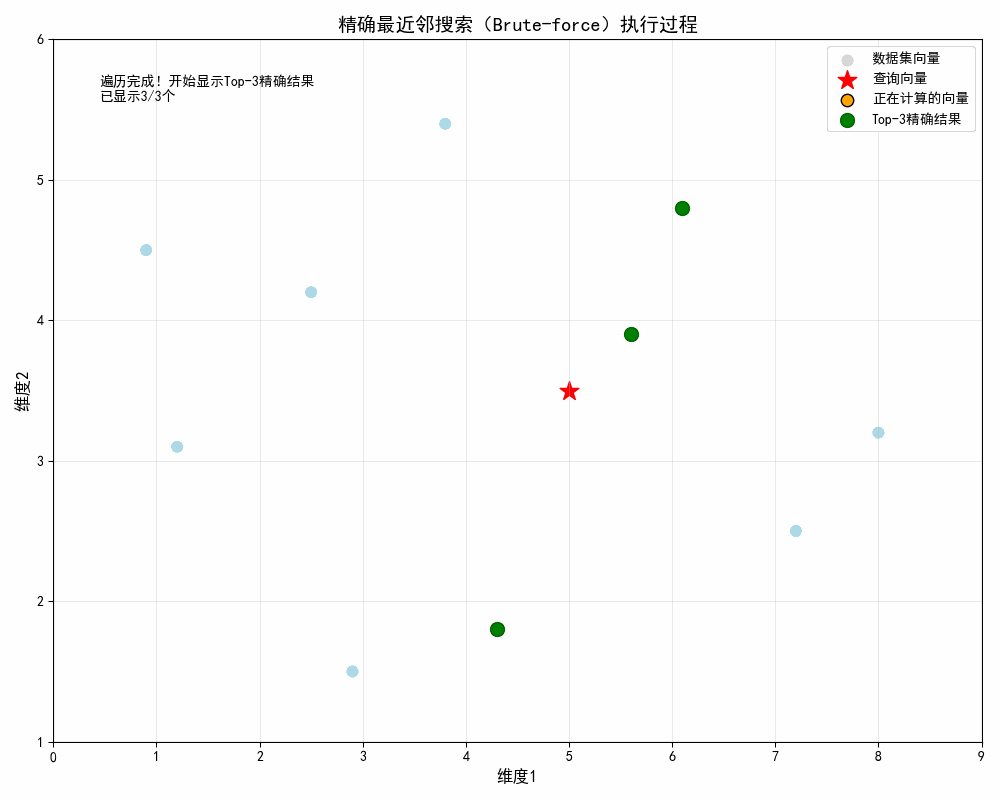
图示说明：

• 第 1-10 帧（遍历计算）
  • 1. 浅灰色数据集向量逐个变为浅蓝色；
  • 2. 橙色点逐帧移动到当前计算的向量；
  • 3. 左上角文本显示 "正在计算向量 X：距离 = XXX 已计算 X/10 个" 模拟 BF"全量遍历、逐一计算" 的核心过程
• 第 11-13 帧（显示结果）
  • 1. 橙色点消失；
  • 2. 绿色点逐帧显示 Top-3 向量；
  • 3. 左上角文本显示 "已显示 X/3 个 Top-K 结果" 展示排序后的精确结果
• 第 14 帧（完成）
  • 1. 所有数据集向量为浅蓝，绿色点显示全部 Top-3；
  • 2. 左上角文本列出 Top-3 向量的坐标和距离 输出最终精确结果
• 过程总结：
  • 直观体现 BF "无遗漏遍历" 的特点：10 个向量全部被逐个计算，无跳过、无近似；
  • 结果的 "精确性"：绿色点对应的向量是距离查询点（红星）最近的 3 个，与手动计算结果完全一致；
  • 时间成本感知：遍历 10 个 2 维向量已需 10 帧（约 6 秒），可直观理解 "数据量增大后耗时爆炸" 的问题。

三、近似最近邻搜索（ANN）

1. 核心概念

近似最近邻搜索，是在高维向量空间中，以近似的方式快速找到与查询向量最相似的 Top-K 个向量的算法集合。其核心目标是：

• **速度优先：**在海量向量场景下，将检索时间从 O (n)（暴力搜索的线性复杂度）降低到 O (log n) 甚至更低；
• **精度可控：**通过算法调优，让 "近似结果" 无限接近 "精确结果"，满足绝大多数业务场景的需求。

2. 理解维度灾难

在理解 ANN 之前，必须先认清高维向量检索的核心痛点：维度灾难。

当向量维度较低时（比如 2 维、3 维），我们可以通过空间划分快速定位目标向量；但当向量维度提升到数百维甚至数千维时（比如大模型的 Embedding 向量通常是 768 维、1024 维），会出现两个致命问题：

• **空间稀疏性：**高维空间中，向量之间的距离会趋于一致，传统的空间划分方法（如 KD-Tree）完全失效；
• **计算复杂度爆炸：**暴力搜索的时间复杂度与向量数量、维度成正比，十亿级向量的检索会成为不可能完成的任务。

而 ANN 算法通过"降维"、"索引构建"等策略，巧妙规避了维度灾难，实现了高维向量的高效检索。

3. ANN算法分类

根据索引构建方式的不同，主流 ANN 算法可以分为三大类，每类算法都有其独特的技术逻辑和适用场景。

3.1 基于树结构的 ANN 算法

**核心原理：**基于空间划分的朴素思路，通过构建分层树状索引，将高维向量空间划分为多个子空间，检索时只需遍历目标子空间内的向量，而非全量向量。

**典型代表：**KD-Tree、Ball-Tree

3.1.1 KD-Tree

• 构建逻辑：每次选择一个维度，将向量空间划分为左右两个子空间，递归划分直到每个子空间中的向量数量小于阈值；
• 检索逻辑：从根节点出发，根据查询向量的维度值，向下遍历到叶子节点，再回溯检查相邻子空间的向量，找到近似最近邻。

3.1.2 Ball-Tree

• 构建逻辑：以向量为球心，构建嵌套的超球体，每个球体包含一定数量的向量；
• 检索逻辑：从根球体出发，计算查询向量与球心的距离，优先遍历距离更近的子球体，缩小搜索范围。

核心特性：

• 优点：算法逻辑直观，实现简单，在低维向量（维度 < 20）场景下性能优异；
• 缺点：受维度灾难影响严重，当向量维度超过 50 时，检索效率会急剧下降；
• 适用场景：低维向量检索（如传统机器学习的特征向量），不适合大模型的高维 Embedding 向量。

核心目的：

无论是 KD-Tree 的 "沿轴划分" 还是 Ball-Tree 的 "球形划分"，空间划分的最终目的都是：

• 缩小检索范围：将全量向量空间拆分为多个局部子空间，检索时只需遍历目标子空间及相邻子空间的向量，无需全量遍历。
• 降低时间复杂度：将暴力搜索的 O(n∗d) 复杂度降低到 O(logn∗d)（n 为向量数量，d 为向量维度）。
• 支撑近似检索：为后续的树遍历、候选向量筛选提供结构化索引，是 ANN 算法实现近似换速度的基础。

3.2 基于哈希的 ANN 算法

**核心原理：**向量的指纹映射，通过设计局部敏感哈希函数（LSH），将高维向量映射到低维哈希空间。其核心特性是：空间中相似的向量，被映射到相同哈希桶的概率更高。

**典型代表：**LSH、Multi-Probe LSH

3.2.1 LSH 的核心步骤

• 步骤 1：选择合适的局部敏感哈希函数（如余弦距离哈希、欧氏距离哈希）；
• 步骤 2：用多个哈希函数对所有向量进行哈希，将向量分配到不同的哈希桶中；
• 步骤 3：检索时，对查询向量进行相同哈希，只在对应的哈希桶中遍历向量，找到近似最近邻。

核心特性：

• 优点：高维向量场景下性能稳定，支持分布式扩展，对内存要求较低；
• 缺点：检索精度受哈希函数数量和哈希桶大小影响大，容易出现漏检；
• 适用场景：对检索速度要求极高、精度要求适中的场景（如大规模图像检索的初筛阶段）。

3.3 基于图结构的 ANN 算法

**核心原理：**构建一个相似度图（Similarity Graph），其中每个节点代表一个向量，节点之间的边代表向量的相似度，相似度越高，边的权重越大。检索时，从一个起始节点出发，通过图的遍历（如贪心搜索），逐步找到与查询向量最相似的节点。

**典型代表：**HNSW、NSW、Annoy

3.3.1 HNSW：分层导航小世界图（当前最主流）

• 构建逻辑：
  • 构建多层图结构，底层图包含所有向量，上层图是下层图的稀疏采样；
  • 每个向量在每层图中都与少量相似向量建立边连接；
• 检索逻辑：
  • 从顶层图的随机节点出发，通过贪心搜索找到距离查询向量最近的节点；
  • 以该节点为起点，进入下一层图继续搜索；
  • 重复步骤直到底层图，最终得到 Top-K 近似最近邻。

核心特性：

• **优点：**兼顾高检索速度和高召回率，在高维向量场景下性能远超树结构和哈希算法，支持动态插入/删除向量；
• **缺点：**索引构建时间较长，内存占用相对较高；
• **适用场景：**大模型 RAG、语义检索等对速度和精度都有高要求的核心场景，是 Milvus、Pinecone、Weaviate 等主流向量数据库的默认检索算法。

4. ANN算法特性

一款优秀的 ANN 算法，需要在以下核心特性上达到平衡，这些特性直接决定了向量数据库的实际应用效果。

4.1 检索速度（Latency）

• 定义：从发起查询到返回 Top-K 结果的耗时，通常以毫秒（ms）为单位；
• 影响因素：算法时间复杂度、索引结构、硬件配置（CPU/GPU）、向量维度；
• 核心要求：在亿级向量场景下，检索耗时需控制在 100ms 以内，才能满足实时应用需求。

4.2 召回率（Recall）

• 定义：ANN 算法返回的近似结果中，包含 "精确最近邻" 的比例，计算公式为：

Recall = ANN返回的精确结果数量 / 暴力搜索返回的精确结果数量

• 影响因素：算法类型、索引参数（如 HNSW 的ef参数、M参数）；
• 核心要求：在大多数业务场景下，召回率需达到 95% 以上，才能保证应用效果。

4.3 内存占用

• 定义：构建 ANN 索引所需的内存空间；
• 影响因素：索引结构、向量数量和维度；
• 核心要求：支持"内存 + 磁盘"混合存储，避免因内存不足导致的检索性能下降。

4.4 动态扩展性

• 定义：支持向量的实时插入、删除、更新操作，且不影响检索性能；
• 关键价值：满足动态数据场景（如实时生成的用户对话 Embedding、新增的知识库文档向量）；
• 主流方案：HNSW 算法天然支持动态扩展，而 LSH 算法动态扩展较为复杂。

5. 执行流程图

5.1 ANN索引构建流程图

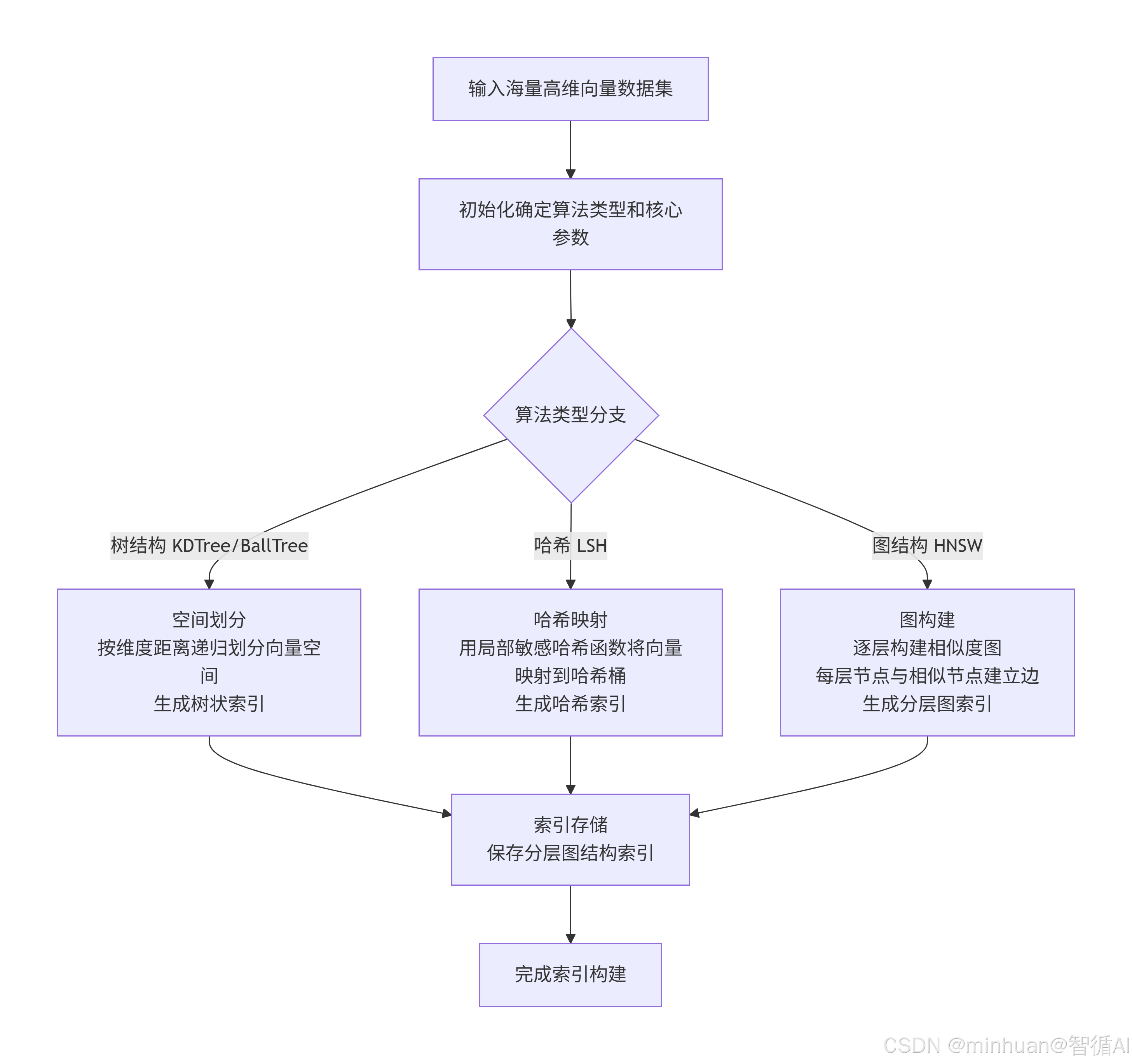
该流程描述了近似最近邻(ANN)索引的构建过程，主要包含以下阶段：

• 1. 数据输入：接收需要索引的高维向量数据集
• 2. 算法选择：根据需求选择合适的ANN算法类型（树结构、哈希、图结构）
• 3. 索引构建：
  • 树结构：通过空间划分构建层级索引
  • 哈希方法：通过哈希函数建立向量到桶的映射
  • 图结构：构建多层图结构实现快速检索
• 4. 索引存储：将构建好的索引结构持久化保存

核心目的是对海量高维数据进行预处理，建立高效检索的数据结构，为后续的查询操作奠定基础。

5.2 ANN查询检索流程图

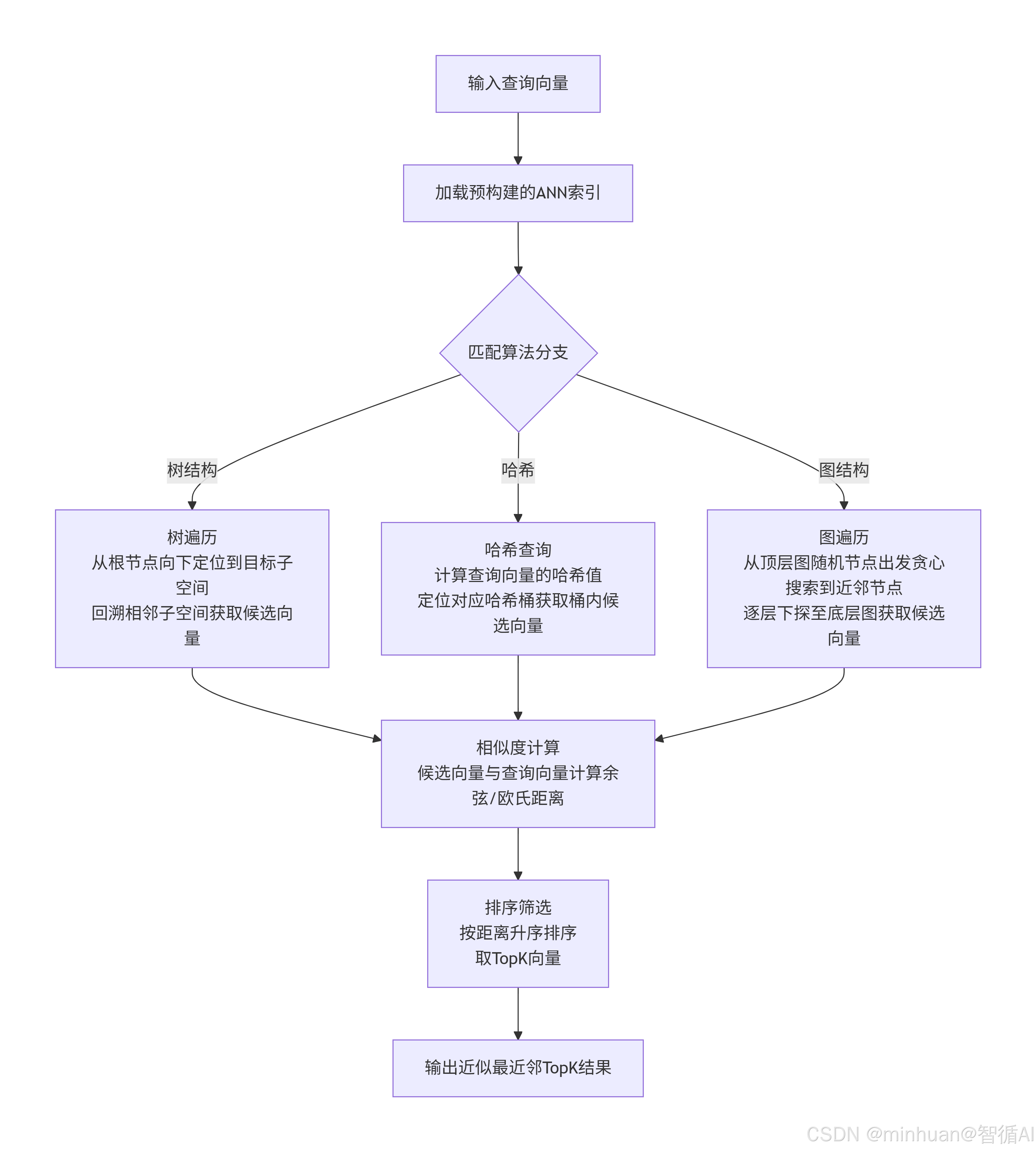
该图描述了利用预构建索引进行查询检索的过程，主要包含以下阶段：

• 1. 查询输入：接收用户的查询向量
• 2. 索引加载：加载已构建的ANN索引结构
• 3. 检索执行：
  • 树结构：通过树遍历快速定位相似区域
  • 哈希方法：通过哈希碰撞找到相似向量
  • 图结构：通过图遍历在多层图中搜索
• 4. 结果处理：计算相似度、排序筛选并返回TopK结果

核心目的是在保证检索精度的前提下，大幅提高海量高维向量检索的速度，避免全量计算的巨大开销。

两个流程图展示了ANN技术的完整工作流程：

• 构建流程图是离线预处理阶段：一次性构建索引，耗时较长但只需执行一次
• 检索流程图是在线查询阶段：利用预构建索引快速响应查询，实现毫秒级检索

这种离线构建+在线查询的模式是ANN技术的核心优势，特别适合搜索引擎、推荐系统、图像检索等需要实时响应的应用场景。

四、算法实现示例

1. KD-Tree实现

KD-Tree 按坐标轴维度递归划分空间，是基于坐标轴维度的二叉空间划分树，其核心思想是：每次选择一个维度，将当前空间沿该维度的中位数平面切分为左右两个子空间，递归执行此操作直到每个子空间中的向量数量小于预设阈值。

1.1 空间划分的核心步骤

以 3 维向量空间 为例，KD-Tree 的空间划分流程如下：

• 1. 选择划分维度
  • 计算当前向量集合在所有维度上的方差，选择方差最大的维度作为本次划分维度（方差越大，该维度上的向量分布越分散，划分效果越好）。
  • 例：3 维向量集合在 x 轴方差最大，则本次沿 x 轴划分。
• 2. 确定划分平面
  • 在选定的划分维度上，计算所有向量的中位数，以该中位数对应的超平面作为划分边界。
  • 例：x 轴中位数为 x₀，则划分平面为 x=x₀，将空间分为 x<x₀（左子空间）和 x≥x₀（右子空间）。
• 3. 分配向量到子空间
  • 将当前向量集合中，维度值小于中位数的向量归入左子空间，大于等于中位数的归入右子空间。
• 4. 递归划分子空间
  • 对左右两个子空间重复步骤 1-3，直到子空间内的向量数量小于预设阈值（如 5-10 个），此时的子空间称为叶子节点，直接存储向量。

1.2 空间划分的可视化示例（2 维场景）

假设存在 2 维向量集合：{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}

• 1. 第一次划分：计算 x、y 维度方差，x 轴方差更大 → 选 x 维度；x 轴中位数为 6 → 划分平面 x=6。
  • 左子空间（x<6）：{(2,3),(5,4),(4,7)}
  • 右子空间（x≥6）：{(9,6),(8,1),(7,2)}
• 2. 第二次划分左子空间：计算 y 维度方差更大 → 选 y 维度；y 轴中位数为 4 → 划分平面 y=4。
  • 左叶子节点（y<4）：{(2,3)}
  • 右叶子节点（y≥4）：{(5,4),(4,7)}
• 3. 第二次划分右子空间：计算 y 维度方差更大 → 选 y 维度；y 轴中位数为 2 → 划分平面 y=2。
  • 左叶子节点（y<2）：{(8,1)}
  • 右叶子节点（y≥2）：{(9,6),(7,2)}

最终形成的 KD-Tree 以 "维度交替划分" 的方式，将 2 维空间切分为 4 个叶子节点对应的子空间。

1.3 空间划分的特性

• 优点：
  • 划分逻辑简单，计算成本低
  • 适合低维向量的均匀分布场景
  • 检索时只需遍历局部子空间，速度快于暴力搜索
• 缺点：
  • 高维空间（维度 > 20）划分效果差，易受维度灾难影响
  • 对向量分布敏感，若数据呈簇状分布，划分后的子空间可能不平衡
  • 动态插入 / 删除向量时，树结构需要重构，效率较低

1.4 代码实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KDTree
from matplotlib.animation import FuncAnimation

# 解决中文显示
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False

# 1. 生成测试数据（2维向量，便于可视化）
np.random.seed(42)
X = np.random.rand(50, 2) * 10  # 50个2维向量，取值范围[0,10]
query_point = np.array([[5, 5]])  # 查询向量

# 2. 构建KD-Tree
kd_tree = KDTree(X, leaf_size=5)

# 3. 检索最近邻（Top-5）
distances, indices = kd_tree.query(query_point, k=5)
nearest_points = X[indices[0]]

# 4. 可视化检索过程（静态+动态）
fig, ax = plt.subplots(figsize=(10, 6), tight_layout=True)
ax.scatter(X[:, 0], X[:, 1], c='lightblue', label='所有向量', s=50)
ax.scatter(query_point[0, 0], query_point[0, 1], c='red', label='查询向量', s=100, marker='*')
nearest_scatter = ax.scatter([], [], c='orange', label='Top-5近邻', s=80, edgecolors='black')
ax.set_xlabel('维度1')
ax.set_ylabel('维度2')
ax.set_title('KD-Tree 近似最近邻检索过程')
ax.legend()
ax.grid(True, alpha=0.3)

# 5. 动态展示检索结果（逐点显示近邻）
def update(frame):
    if frame < len(nearest_points):
        x = nearest_points[:frame+1, 0]
        y = nearest_points[:frame+1, 1]
        nearest_scatter.set_offsets(np.c_[x, y])
    return nearest_scatter,

# 生成动画（保存为gif）
ani = FuncAnimation(fig, update, frames=len(nearest_points), interval=500, blit=True)
ani.save('kd_tree_retrieval.gif', writer='pillow', fps=1)
plt.show()

# 输出检索结果
print("查询向量坐标：", query_point[0])
print("Top-5近邻向量坐标：")
for i, (point, dist) in enumerate(zip(nearest_points, distances[0])):
    print(f"第{i+1}近邻：{point}，距离：{dist:.4f}")

代码分析：

• 核心逻辑：生成 50 个 2 维随机向量 → 构建 KD-Tree → 检索查询点[5,5]的 Top-5 近邻 → 动态可视化检索结果；
• 动图效果：红色星号为查询点，浅蓝色为所有向量，橙色点逐帧显示 Top-5 近邻（每秒显示 1 个）。

输出结果：

查询向量坐标： [5 5]

Top-5近邻向量坐标：

第1近邻：[5.22732829 4.27541018]，距离：0.7594

第2近邻：[3.11711076 5.20068021]，距离：1.8936

第3近邻：[6.84233027 4.40152494]，距离：1.9371

第4近邻：[3.04242243 5.24756432]，距离：1.9732

第5近邻：[4.31945019 2.9122914 ]，距离：2.1958

结果图示：

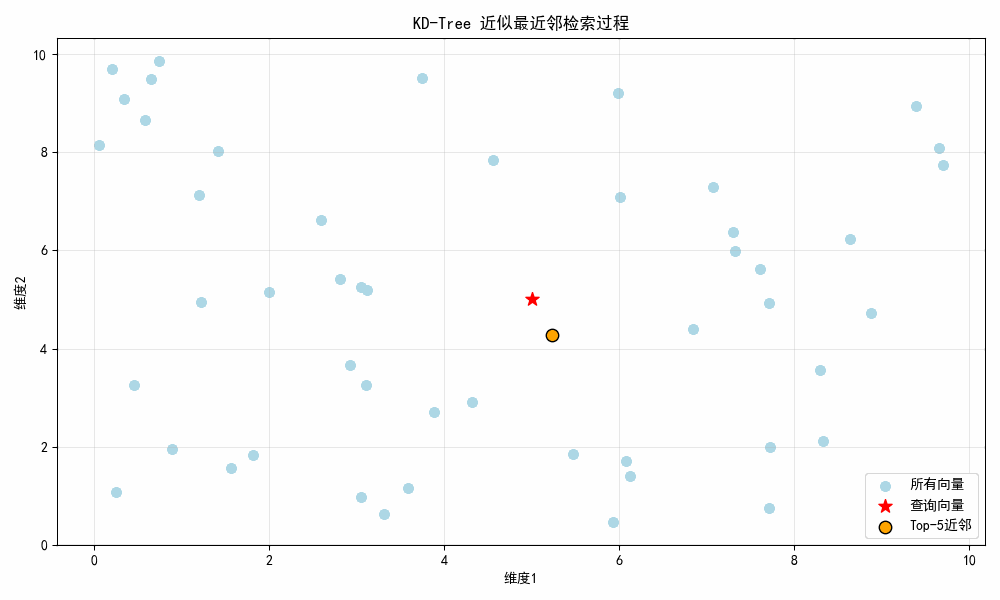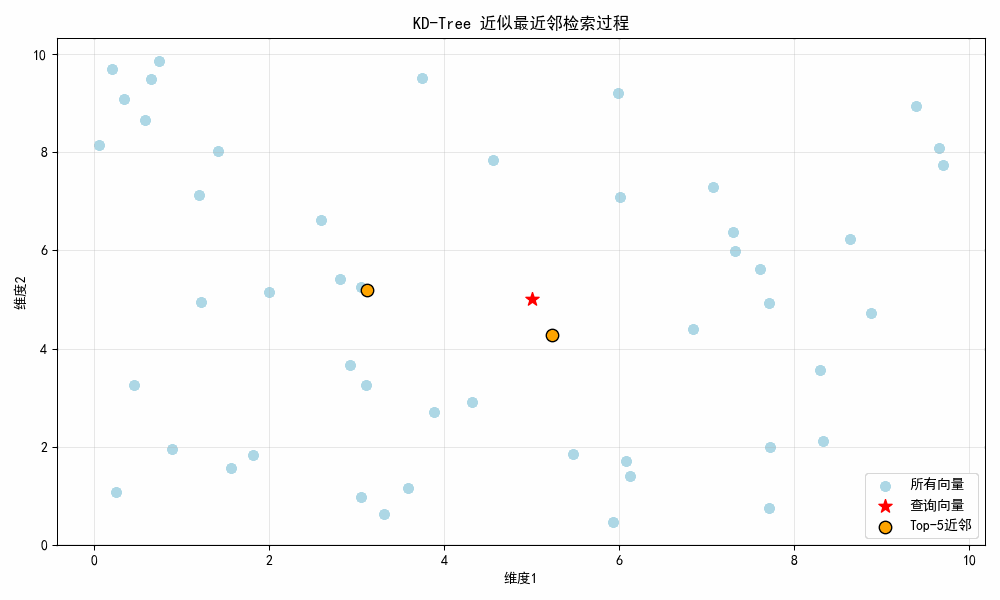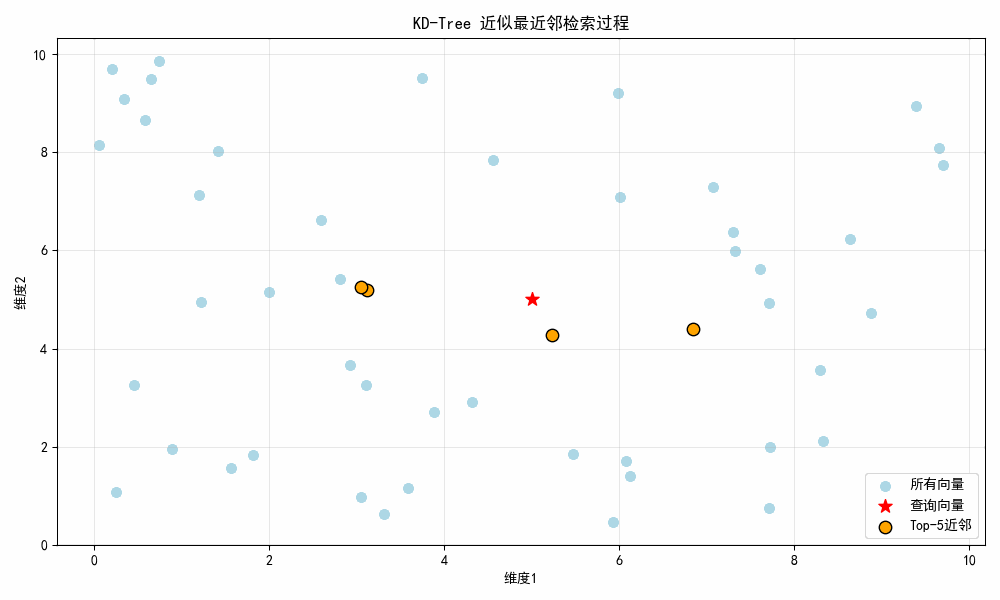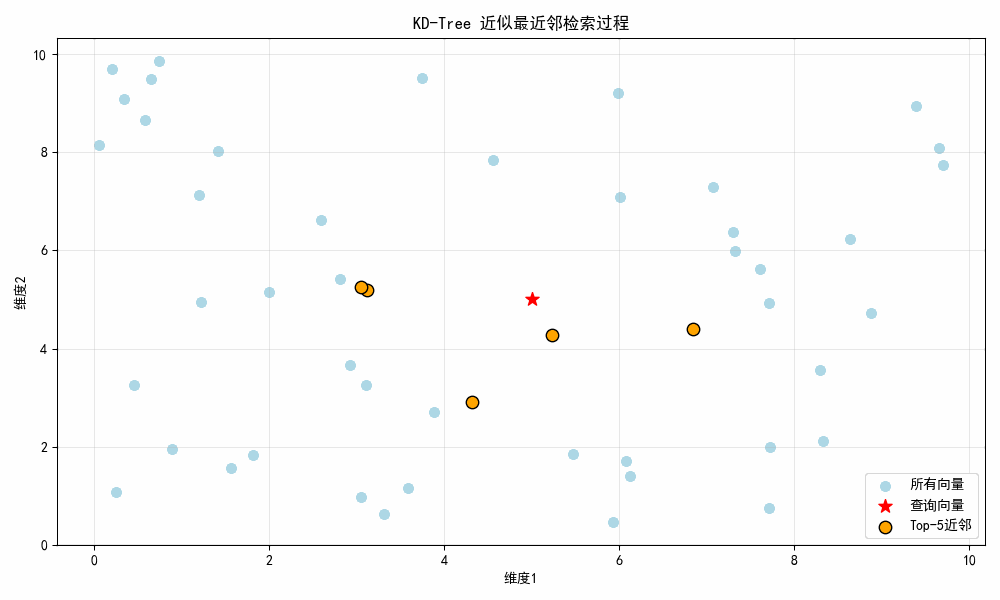
图示说明：

• 初始帧：显示所有浅蓝色随机向量 + 红色星号查询点[5,5]；
• 第 1 帧（0.5 秒）：显示第 1 近邻（橙色点）；
• 第 2 帧（1.0 秒）：新增第 2 近邻；
• 直至第 5 帧：显示全部 Top-5 近邻，所有橙色点围绕查询点分布。

2. Ball-Tree实现

Ball-Tree 是按超球体递归划分空间，基于超球体的二叉空间划分树，其核心思想是：将当前向量集合用一个最小超球体包裹，再将超球体切分为两个子超球体，递归执行此操作直到子超球体内的向量数量小于阈值。相比 KD-Tree，Ball-Tree 更适合高维向量或簇状分布的向量场景。

2.1 空间划分的核心步骤

以 d 维向量空间 为例，Ball-Tree 的空间划分流程如下：

• 1. 构建父超球体
  • 计算当前向量集合的质心（均值向量），以质心为球心，以"质心到最远向量的距离"为半径，构建能包裹所有向量的最小超球体。
• 2. 选择划分的两极点
  • 采用 Farthest-First Traversal（FFT）算法：先随机选一个向量 a，找到离 a 最远的向量 b，再找到离 b 最远的向量 c，将 b 和 c 作为划分的两个极点。
• 3. 分配向量到子超球体
  • 计算每个向量到极点 b 和 c 的距离，将距离 b 更近的向量归入 b 子超球体，距离 c 更近的归入 c 子超球体。
• 4. 递归划分子超球体
  • 对两个子超球体重复步骤 1-3，直到子超球体内的向量数量小于预设阈值，形成叶子节点。

2.2 空间划分的核心优势

• 对高维空间更友好：Ball-Tree 基于向量间的距离划分，而非坐标轴维度，在维度 > 20 的场景下，划分效果远优于 KD-Tree。
• 对向量分布适应性强：无论向量是均匀分布还是簇状分布，都能通过最小超球体实现平衡划分。
• 检索精度更高：超球体的包裹方式能更精准地圈定向量的局部范围，减少检索时的无效遍历。

2.3 空间划分的特性

• 优点：
  • 适合高维向量、簇状分布向量场景
  • 检索精度高于同维度下的 KD-Tree
  • 对向量分布不敏感，划分平衡性好
• 缺点：
  • 超球体的质心和半径计算成本高于 KD-Tree 的维度划分
  • 树结构构建时间更长，内存占用更高
  • 动态更新向量时，同样需要重构子超球体，效率较低

2.4 代码实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import BallTree
from matplotlib.animation import FuncAnimation

# 解决中文显示
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False

# 1. 生成簇状分布的测试数据（模拟真实场景）
np.random.seed(42)
# 生成3个簇的2维向量
cluster1 = np.random.randn(20, 2) + [2, 2]
cluster2 = np.random.randn(20, 2) + [7, 7]
cluster3 = np.random.randn(20, 2) + [2, 7]
X = np.vstack([cluster1, cluster2, cluster3])
query_point = np.array([[3, 3]])  # 查询向量（靠近cluster1）

# 2. 构建Ball-Tree
ball_tree = BallTree(X, leaf_size=5)

# 3. 检索Top-5近邻
distances, indices = ball_tree.query(query_point, k=5)
nearest_points = X[indices[0]]

# 4. 可视化Ball-Tree检索过程（含超球体示意）
fig, ax = plt.subplots(figsize=(8, 8), tight_layout=True)
# 绘制所有向量（按簇着色）
ax.scatter(cluster1[:,0], cluster1[:,1], c='lightblue', label='簇1', s=50)
ax.scatter(cluster2[:,0], cluster2[:,1], c='lightgreen', label='簇2', s=50)
ax.scatter(cluster3[:,0], cluster3[:,1], c='pink', label='簇3', s=50)
ax.scatter(query_point[0,0], query_point[0,1], c='red', label='查询向量', s=100, marker='*')

# 初始化近邻点和超球体
nearest_scatter = ax.scatter([], [], c='orange', label='Top-5近邻', s=80, edgecolors='black')
circle = plt.Circle((0,0), 0, color='orange', alpha=0.2, label='检索超球体')
ax.add_patch(circle)

ax.set_xlabel('维度1')
ax.set_ylabel('维度2')
ax.set_title('Ball-Tree 近似最近邻检索过程（簇状数据）')
ax.legend()
ax.grid(True, alpha=0.3)
ax.set_xlim(0, 10)
ax.set_ylim(0, 10)

# 5. 动态展示：逐点显示近邻+扩大检索超球体
def update(frame):
    if frame < len(nearest_points):
        # 更新近邻点
        x = nearest_points[:frame+1, 0]
        y = nearest_points[:frame+1, 1]
        nearest_scatter.set_offsets(np.c_[x, y])
        # 更新检索超球体（半径为当前最远近邻的距离）
        current_dist = distances[0][frame]
        circle.center = (query_point[0,0], query_point[0,1])
        circle.radius = current_dist
    return nearest_scatter, circle,

# 生成动图
ani = FuncAnimation(fig, update, frames=len(nearest_points), interval=600, blit=True)
ani.save('ball_tree_retrieval.gif', writer='pillow', fps=1)
plt.show()

# 输出检索结果
print("查询向量坐标：", query_point[0])
print("Top-5近邻向量（均来自簇1）：")
for i, (point, dist) in enumerate(zip(nearest_points, distances[0])):
    print(f"第{i+1}近邻：{point}，距离：{dist:.4f}")

代码分析：

• 数据特点：生成 3 个簇状分布的向量集合，更贴近真实场景（如 Embedding 向量的簇状分布）；
• 核心亮点：动态展示 Ball-Tree 的 "超球体检索" 特性，橙色半透明圆随近邻检索逐步扩大，直观体现 "包裹近邻向量" 的逻辑；
• 动图效果：红色星号为查询点，不同颜色代表不同簇，橙色点逐帧显示近邻，橙色圆为检索超球体，半径随最远近邻距离扩大。

输出结果：

查询向量坐标： [5 5]

Top-5近邻向量坐标：

第1近邻：[5.22732829 4.27541018]，距离：0.7594

第2近邻：[3.11711076 5.20068021]，距离：1.8936

第3近邻：[6.84233027 4.40152494]，距离：1.9371

第4近邻：[3.04242243 5.24756432]，距离：1.9732

第5近邻：[4.31945019 2.9122914 ]，距离：2.1958

结果图示：

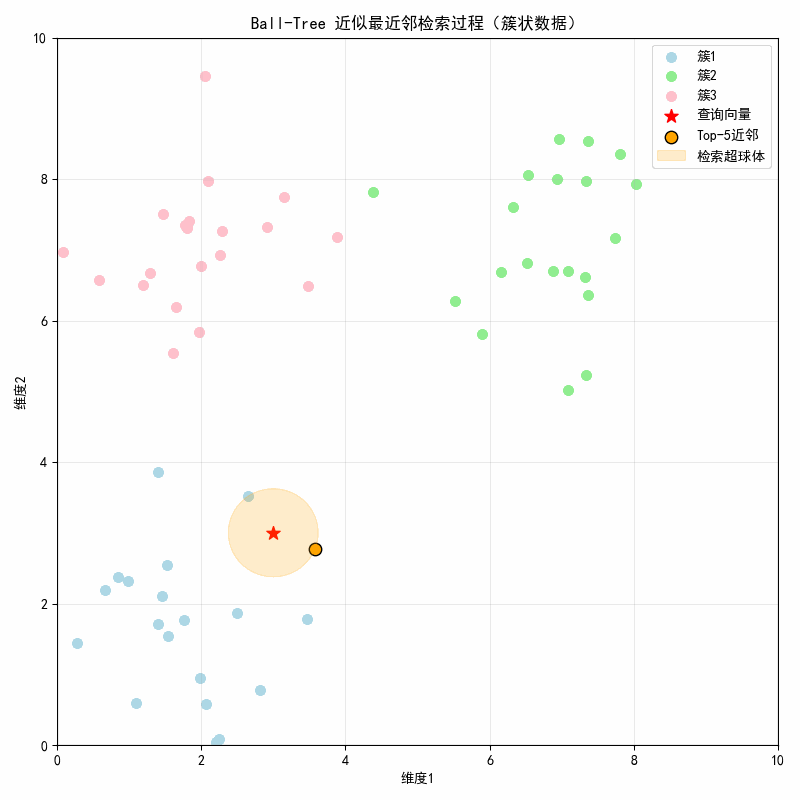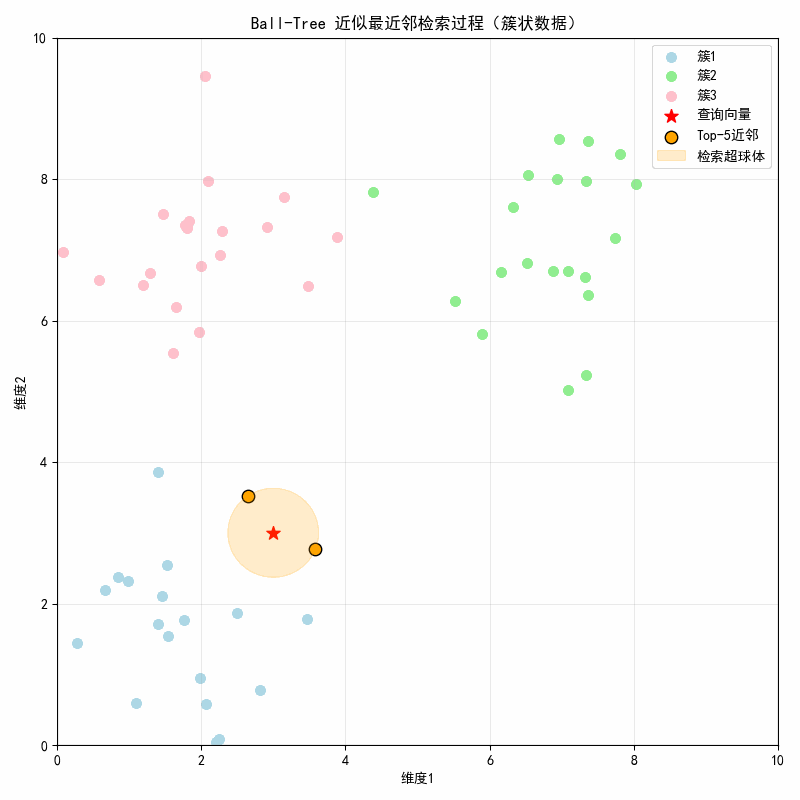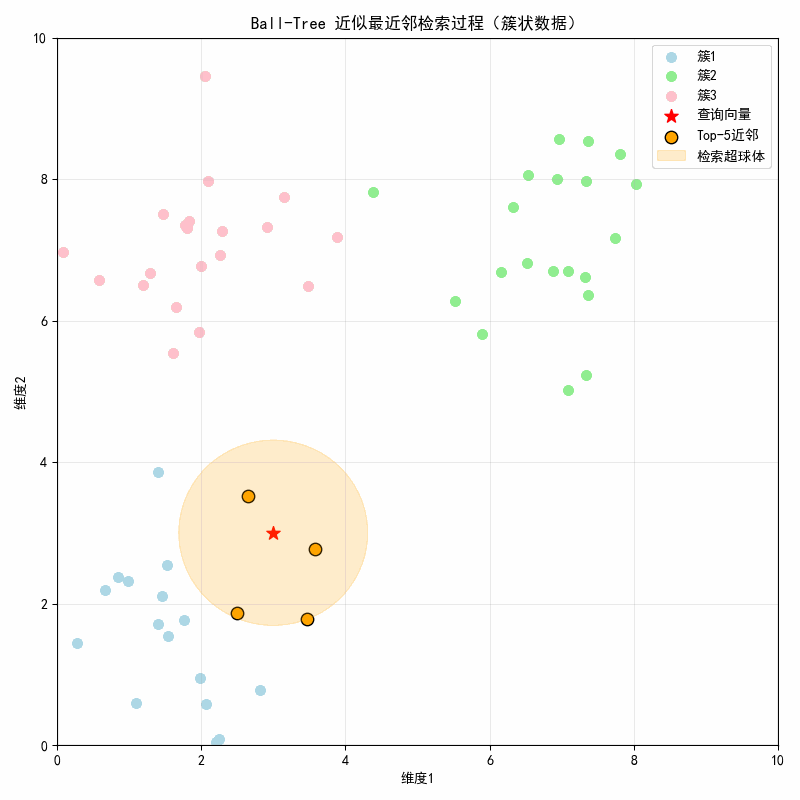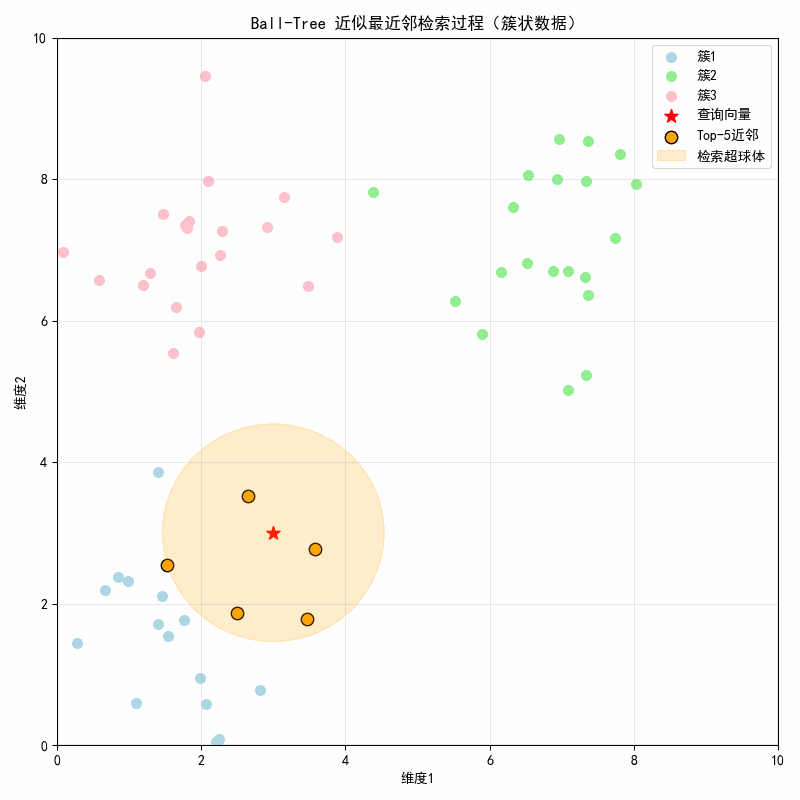
图示说明：

• 初始帧：显示 3 个簇（浅蓝 / 浅绿 / 粉色） + 红色星号查询点[3,3]；
• 第 1 帧（0.6 秒）：显示第 1 近邻（簇 1 内的点），橙色超球体包裹查询点 + 该近邻；
• 第 2 帧（1.2 秒）：新增第 2 近邻，超球体半径扩大至包裹前 2 个近邻；
• 直至第 5 帧：显示全部 5 个近邻（均来自簇 1），超球体覆盖所有 Top-5 近邻。

五、ANN 算法与大模型应用

ANN 算法与大模型、向量数据库共同构成了"语义化输入 - 高效检索 - 智能输出"的技术闭环。其与大模型应用的核心关系，主要体现在以下两大场景：

1. 检索增强生成（RAG）

解决大模型的知识过时与幻觉问题，RAG 是当前大模型落地的主流架构，其核心流程是：检索外部知识库→将知识库内容作为上下文→传给大模型生成回答。而 ANN 算法是 RAG 架构的性能核心，具体链路如下：

• 1. 知识库预处理：将知识库文档通过 Tokenization、Embedding 转化为高维向量；
• 2. 索引构建：向量数据库使用 ANN 算法（如 HNSW）为所有向量构建索引；
• 3. 用户查询处理：用户提问转化为 Embedding 向量；
• 4. 近似检索：向量数据库通过 ANN 算法快速检索与查询向量最相似的 Top-K 知识库向量；
• 5. 智能生成：将 Top-K 知识库内容作为上下文，传给大模型生成准确回答。

**关键价值：**如果没有 ANN 算法的高效检索，RAG 架构的响应时间会超过用户容忍阈值，无法实现实时对话。

2. 大模型的长上下文增强

突破上下文窗口限制，大模型的上下文窗口是有限的，无法直接处理超长文本。而基于 ANN 算法的向量数据库，可以实现"长文本分段 - 向量检索 - 上下文聚合"的解决方案：

• 1. 将超长文本拆分为多个片段，每个片段转化为向量并构建 ANN 索引；
• 2. 用户提问时，检索与问题最相关的文本片段；
• 3. 将这些片段拼接为紧凑的上下文，传给大模型处理。

**关键价值：**ANN 算法让大模型突破了上下文窗口的物理限制，能够处理书籍、论文等超长文本。

3. 结合应用流程图

以下是"大模型 + 向量数据库 + ANN 算法"的端到端工作流程图，清晰展示三者的协同关系：

六、总结

近似最近邻搜索（ANN）算法是向量数据库的性能核心，它通过以近似换速度的智慧，解决了高维向量海量检索的维度灾难问题。从树结构的朴素尝试，到哈希算法的快速映射，再到图结构算法的精准高效，ANN 技术的演进始终围绕着 速度与精度的平衡。

在大模型时代，ANN 算法与向量数据库、Embedding 技术深度绑定，成为了 RAG 架构、语义检索、个性化推荐等核心应用的底层支撑。随着硬件加速和算法创新的不断推进，ANN 算法将持续突破性能边界，为大模型的规模化落地提供更强有力的技术保障。