------从黎曼流形错位到语义检索失效的系统性研究
1. 绪论:语义检索中的同构假设及其崩塌
在当代自然语言处理(NLP)与神经信息检索(NIR)体系中,向量嵌入(Vector Embedding)是连接离散符号与连续语义空间的桥梁。
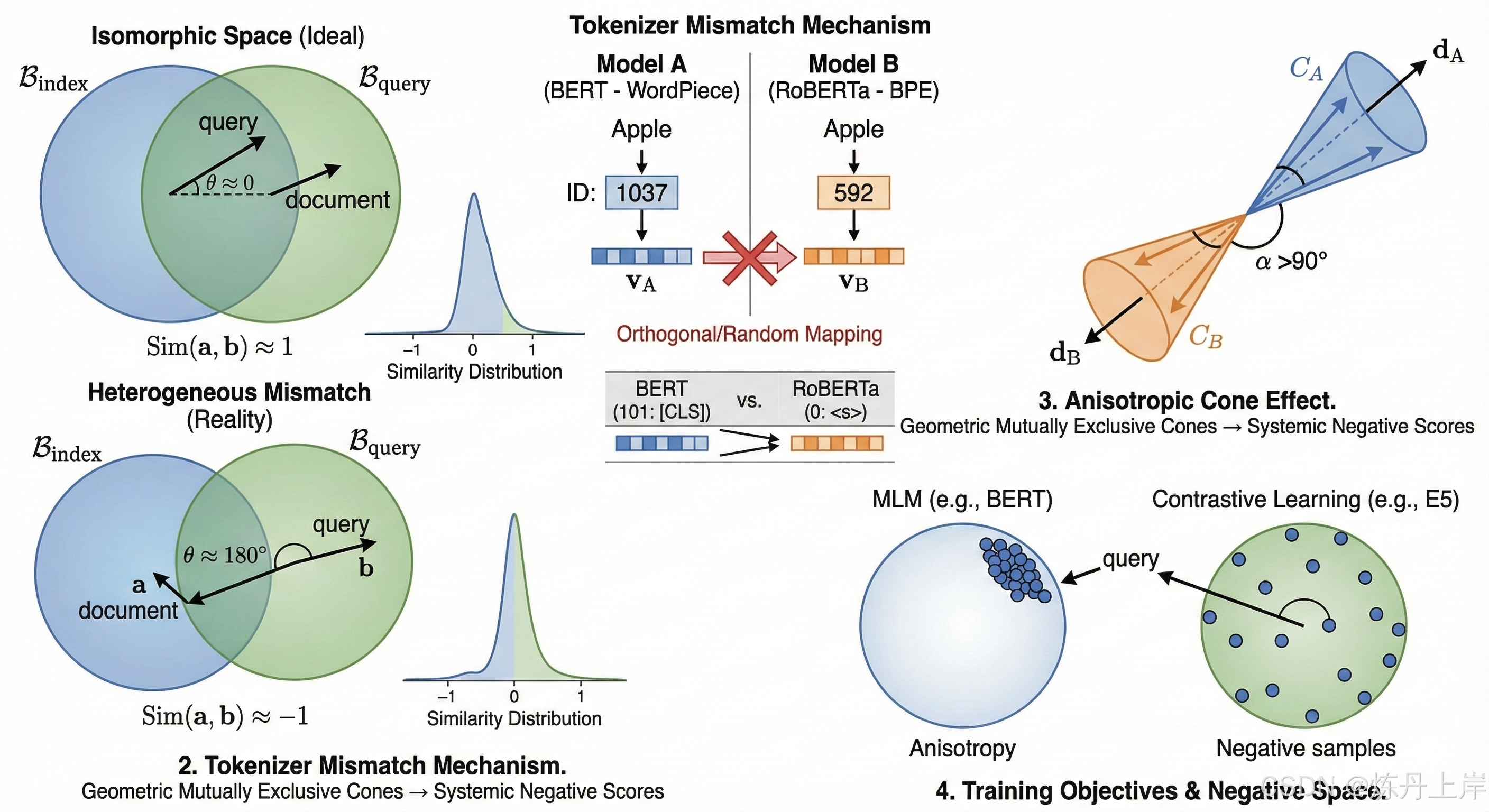
- 同构空间假设 (Isomorphic Space Hypothesis): 检索增强生成(RAG)和语义搜索的核心建立在一个公理化假设之上------即文档编码器(Document Encoder)和查询编码器(Query Encoder)将实体映射到同一个共享度量空间 中。在此空间内,距离或角度单调反映语义相关性。
- 异构模型配置 (Heterogeneous Model Configuration): 工程实践中,入库(Indexing)与检索(Retrieval)阶段使用不一致的嵌入模型(如 ),导致"向量空间失配"。
核心病态现象: 系统计算出的余弦相似度出现大量负值。这不仅意味着低相关性,更揭示了底层数学模型的根本性失效------即高维空间中的"反向"或"对抗"几何关系。
2. 向量空间的几何基础与负相似度的数学本质
要理解负分,必须厘清高维空间中余弦相似度的物理意义。
2.1 余弦相似度的代数定义
给定文档向量 和查询向量 ,其余弦相似度定义为:
- ****: 语义高度相关 。
- ****: 语义正交/无关。
- ****: 语义对立或数学上的反向。
2.2 异构坐标系下的点积失效
在模型不匹配时,我们实际上是在计算两个不同基底( vs )下的向量内积。潜在空间之间存在未知的正交变换矩阵 和平移向量 :
此时的检索计算 等价于 。由于 的随机性,这在数学上等价于两个随机高维向量的点积。
2.3 高维空间中的随机正交性 (Johnson-Lindenstrauss 引理)
根据高维概率论,从各向同性分布中抽取的两个随机向量,其夹角高度集中在 附近。点积 分布近似为:
关键洞察: 异构模型导致的"负分",本质上是相关性退化为随机噪声的结果。随机噪声在高维球面上有一半概率表现为钝角,因此约 50% 的文档呈现负分。
3. 架构层的蝴蝶效应:分词器(Tokenizer)的语义断裂
导致向量空间正交的工程起点通常是"分词器失配"(Tokenizer Mismatch)。
3.1 词汇表 ID 的语义错乱
嵌入层是一个查找表 。不同模型家族的分词算法完全不同:
| 特性 | BERT (WordPiece) | RoBERTa (Byte-Level BPE) |
|---|---|---|
| 词汇表大小 | ~30,522 | ~50,265 |
| 空格处理 | 忽略或作为分隔符 | 视为空格字符 Ġ 的一部分 |
| 未知词处理 | [UNK] |
字节降级,几乎无 [UNK] |
| 特殊 Token | [CLS] (101) |
<s> (0) |
错位演示: 单词 "Apple" 在模型 A 中 ID 为 1037,在模型 B 中 ID 为 592。若混用,则是完全的随机映射 (Complete Random Mapping),生成的向量在高维空间中不仅正交,且极大概率指向相反半球。
3.2 特殊 Token 的聚合灾难
入库模型可能将语义压缩在 ID 101,而检索模型试图从 ID 0 提取。提取出的 实际上是随机初始化的噪声,导致结果围绕 0 波动且大概率为负。
4. 拓扑学视角:各向异性与锥形效应 (The Cone Effect)
除了随机性,现代语言模型的"表示退化"现象使问题系统化。
4.1 表示退化 (Representation Degeneration)
- 现象: 预训练模型(如 BERT)生成的向量并非均匀分布,而是挤压在狭窄的圆锥体(Cone)内。
- 原因: Softmax 损失函数中的频率偏差(高频词主导梯度)。
- 同构表现: 圆锥内向量相似度普遍较高(如 >0.8)。
4.2 异构锥体的几何互斥
当模型 A 的圆锥 与模型 B 的圆锥 交互时,由于两个圆锥的中心轴方向 和 是独立随机形成的,其夹角 极大概率很大。
后果: 则 中所有向量与 中所有向量的点积均倾向于负值。此时负分不再是噪声,而是全局方向性偏差 (Global Directional Bias)。
5. 训练目标函数的差异与负样本空间
5.1 MLM vs. 对比学习 (Contrastive Learning)
- MLM (BERT): 编码句法和局部共现,向量分布混乱且存在各向异性。
- 对比学习 (SimCSE, E5): 目标是最大化正样本相似度,最小化负样本相似度。
影响: 显式地将负样本推向与锚点正交或相反的方向,充分利用超球面。
5.2 空间利用策略的冲突
当对比学习模型(激进利用球面)与 MLM 模型(聚拢在小区域)混用时,查询向量可能位于球面的任意方向,而入库向量仅占据极小表面积。这意味着绝大多数查询向量将落在入库向量簇的"背面",导致系统性负分。
6. 工程实践中的度量陷阱
6.1 点积与余弦的混淆
许多向量数据库默认使用内积(IP)。若模型输出未归一化,且夹角为钝角,负分会被模长放大(如 -25),造成极大困扰。
6.2 维度截断与填充
强行将 1536 维向量截断或填充至 768 维,会破坏全息表示。截断后的向量成为残缺的随机向量,落入随机分布区间(即包含大量负分)。
7. 解决方案与系统一致性重构
针对异构模型导致的负分,唯一的方案是重建模型一致性。
- 严格的版本控制: 确保 Indexing 和 Searching 使用完全相同的架构、权重版本(具体到 Checkpoint)和分词器配置。建议在元数据中存储模型签名。
- 重建索引 (Re-indexing): 模型升级时,必须遍历原始文本重新计算 Embedding。过渡期应采用双写与灰度策略,切勿交叉查询。
- 跨模型对齐 (Procrustes Alignment): 若只有旧向量,可尝试训练线性变换矩阵 ,将旧空间"旋转"对齐到新空间。
8. 结论
异构向量空间失配导致的负分现象,是高维语义空间拓扑结构彻底错位的体现:
- 数学上: 随机向量点积分布以 0 为中心。
- 几何上: 各向异性圆锥体的方向互斥。
- 工程上: 分词器 ID 映射的语义噪声。
保持嵌入模型在全生命周期中的严格一致性,是确保检索系统具备基本物理意义的底线。
附录:核心概念矩阵
| 概念 | 负分贡献机制 | 关键研究支撑 |
|---|---|---|
| Johnson-Lindenstrauss 引理 | 高维随机向量趋向正交,分布中心为 0,导致一半负分 | |
| 各向异性锥 (Anisotropy Cone) | 不同模型的嵌入锥体方向互斥,导致系统性负分 | |
| 分词器失配 (Tokenizer Mismatch) | 输入 ID 错乱导致向量随机化,破坏语义关联 | |
| 对比学习负采样 | 显式推远负样本,利用负半轴空间,加剧异构排斥 |