
在多锚点定位系统中,锚点的选择对定位精度有重要影响。以下是几种常见的锚点选优方法,配合相应的公式和MATLAB代码示例进行详细分析。
文章目录
运行结果
定位结果对比(三列分别是随机锚点选择、最近锚点选择、最优构型选择):
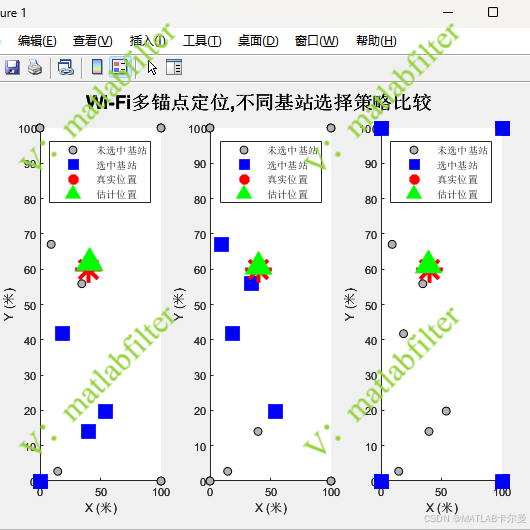
误差对比:
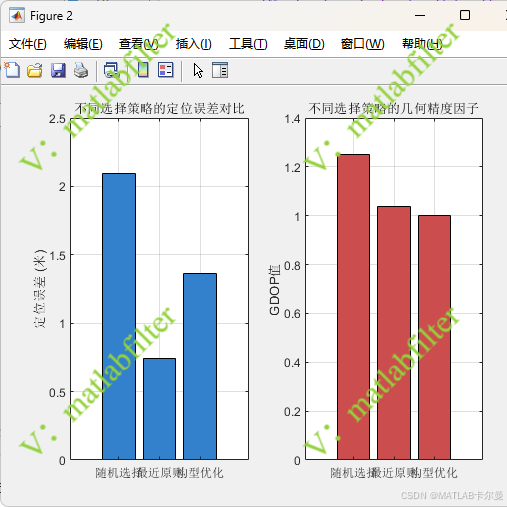
1000次蒙特卡洛后,结果对比:
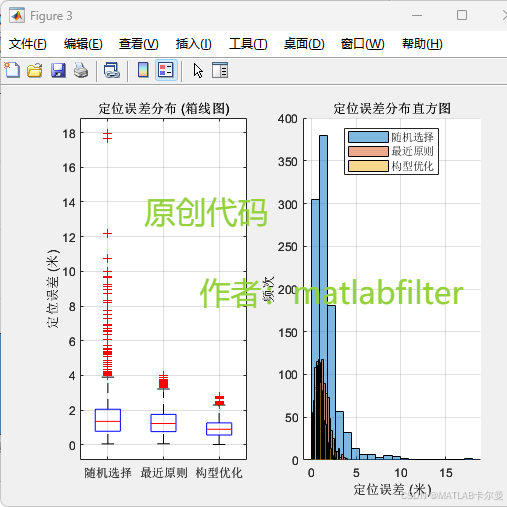
程序简介
基于几何分布的选择
方法描述 :
锚点的几何分布直接影响定位问题的可辨识性 与几何精度因子(GDOP)。一般而言,选择在空间中分布尽量均匀、彼此间夹角较大且距离尺度合理的锚点组合,可以有效降低定位解对观测噪声的敏感性,从而提高定位精度。
设目标位置为
p = [ x , ; y ] T \mathbf{p} = [x,;y]^T p=[x,;y]T
第 (i) 个锚点位置为
a i = [ x i , ; y i ] T \mathbf{a}_i = [x_i,;y_i]^T ai=[xi,;yi]T
目标到第 (i) 个锚点的几何方向向量可表示为
u i = p − a i ∣ p − a i ∣ \mathbf{u}_i = \frac{\mathbf{p}-\mathbf{a}_i}{|\mathbf{p}-\mathbf{a}_i|} ui=∣p−ai∣p−ai
在二维情况下,常通过构造几何矩阵
G = [ u 1 T u 2 T ⋮ u N T ] \mathbf{G} = \begin{bmatrix} \mathbf{u}_1^T \ \mathbf{u}_2^T \ \vdots \ \mathbf{u}_N^T \end{bmatrix} G=[u1T u2T ⋮ uNT]
并以其条件数或几何精度因子作为评价指标,例如
G D O P = t r a c e ! ( ( G T G ) − 1 ) \mathrm{GDOP} = \sqrt{\mathrm{trace}!\left((\mathbf{G}^T\mathbf{G})^{-1}\right)} GDOP=trace!((GTG)−1)
锚点选择原则 可以表述为
min A ; G D O P ( A ) \min_{\mathcal{A}} ; \mathrm{GDOP}(\mathcal{A}) Amin;GDOP(A)
其中 A \mathcal{A} A表示候选锚点组合。
该准则在工程上等价于:锚点尽量包围目标,且相互间夹角尽可能大。
基于距离最小化的选择
方法描述 :
该方法从误差最小化角度出发,通过选择使定位误差最小的锚点组合来提升定位性能。通常假设锚点位置已知,通过比较不同锚点组合下的定位残差或距离误差来完成筛选。
设目标真实位置为 (\mathbf{p}),由某一锚点组合 (\mathcal{A}) 估计得到的位置为 (\hat{\mathbf{p}}(\mathcal{A})),则位置估计误差可定义为
e ( A ) = p ^ ( A ) − p \mathbf{e}(\mathcal{A}) = \hat{\mathbf{p}}(\mathcal{A}) - \mathbf{p} e(A)=p^(A)−p
对应的欧氏距离误差为
J ( A ) = ∣ e ( A ) ∣ 2 J(\mathcal{A}) = |\mathbf{e}(\mathcal{A})|_2 J(A)=∣e(A)∣2
锚点选择问题可表述为以下优化问题:
A ∗ = arg min A ; ∣ p ^ ( A ) − p ∣ 2 \mathcal{A}^\ast = \arg\min_{\mathcal{A}} ; |\hat{\mathbf{p}}(\mathcal{A}) - \mathbf{p}|_2 A∗=argAmin;∣p^(A)−p∣2
在基于测距的定位中,若第 (i) 个锚点的测距值为 (r_i),理论距离为
r ^ i = ∣ p − a ∗ i ∣ \hat{r}_i = |\mathbf{p}-\mathbf{a}*i| r^i=∣p−a∗i∣
则也可基于测距残差构造代价函数
J ( A ) = ∑ ∗ i ∈ A ( r i − ∣ p − a i ∣ ) 2 J(\mathcal{A}) = \sum*{i\in\mathcal{A}} \left(r_i - |\mathbf{p}-\mathbf{a}_i|\right)^2 J(A)=∑∗i∈A(ri−∣p−ai∣)2
通过比较不同锚点组合对应的 (J(\mathcal{A})),选取误差最小的锚点集合作为最终用于定位的锚点。
MATLAB源代码
部分代码:
matlab
% 多锚点Wi-Fi定位系统仿真 - 基于GDOP和距离的基站选择
% 作者:matlabfilter
% 2025-12-14/Ver1
clear; close all; clc;
rng(1);
%% 参数设置
% 仿真区域
area_size = [100, 100]; % 100m x 100m区域
num_anchors = 10; % 总锚点数量
num_selected = 4; % 选择的锚点数量
noise_std = 1; % 测距噪声标准差(米)
% 真实目标位置
true_pos = [40, 60]; % 目标位置
%% 生成锚点位置(基站位置)
anchor_pos = rand(num_anchors, 2) .* area_size;
% 确保至少有几个锚点在边界上(更真实的部署)
anchor_pos(1,:) = [0, 0];
anchor_pos(2,:) = [area_size(1), 0];
anchor_pos(3,:) = [0, area_size(2)];
anchor_pos(4,:) = [area_size(1), area_size(2)];
%% 计算所有锚点到目标的真实距离
true_distances = sqrt(sum((anchor_pos - true_pos).^2, 2));
% 添加测距噪声
measured_distances = true_distances + noise_std * randn(num_anchors, 1);完整代码: