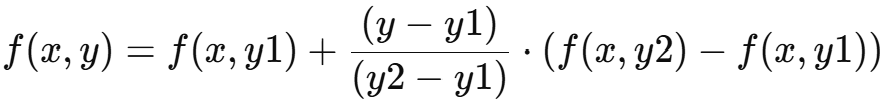一、概述
图像畸变矫正（Image Distortion Correction）是图像处理中的重要任务，通常用于纠正因镜头畸变、拍摄角度等原因造成的图像失真。它的核心原理涉及几何变换，通过对图像进行变换，使其恢复到理想状态。
（一）图像畸变的类型
1.径向畸变（Radial Distortion）：
主要表现为图像中心到边缘的失真，常见的有"桶形畸变"（Barrel Distortion）和"枕形畸变"（Pincushion Distortion）。
桶形畸变：图像的边缘向外膨胀。
枕形畸变：图像的边缘向内收缩。
2.切向畸变（Tangential Distortion）：
由于相机镜头的装配不精确，可能会导致图像出现某些不规则的切向失真。
（二）畸变矫正的原理
图像畸变矫正的目标是通过数学模型来恢复图像的真实几何结构。一般采用如下的模型来进行畸变建模与矫正：
（1）径向畸变模型：
径向畸变模型通常采用以下公式：
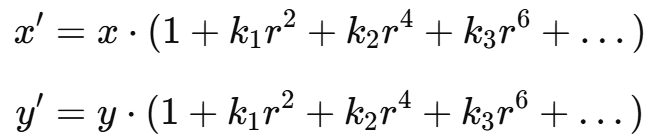
其中，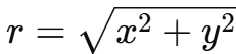
是像素到图像中心的距离，
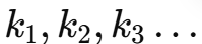是径向畸变系数。
（2）切向畸变模型：
切向畸变的矫正公式可以表示为：
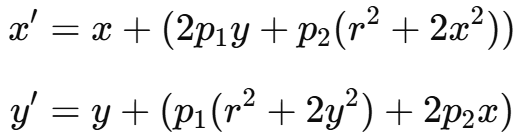
其中，p1和 p2是切向畸变的参数。
（3）实现步骤
矫正顺序：径向畸变先，切向畸变后
通常，径向畸变的矫正应该先执行，然后再进行切向畸变的矫正。这是因为径向畸变是影响图像几何形状的主要因素，它会影响像素点的径向分布，而切向畸变是相对较小的偏差，通常是因为镜头的安装不完全而产生的。首先矫正径向畸变可以避免切向畸变对矫正过程造成的额外影响。
MATLAB提供了强大的图像处理工具箱，可以方便地进行图像畸变矫正。矫正的过程通常包括以下步骤：
- 相机标定
首先，使用棋盘格图像或其他标定图像对相机进行标定，得到相机的内参数、外参数以及畸变系数。
相机标定可以使用MATLAB的 cameraCalibrator 工具。
标定过程中会计算出径向和切向畸变的参数。
- 畸变矫正
使用标定得到的参数进行图像畸变矫正。
（三）FPGA实现原理
在FPGA上实现图像畸变矫正的关键是将畸变矫正的算法高效地映射到硬件上，通常需要关注以下几个方面：
1.数据并行处理：
FPGA的优势在于其并行处理能力。在图像处理过程中，可以将每个像素的处理任务并行化，从而加速图像矫正过程。
2.算法优化：
由于FPGA的资源有限，通常需要对算法进行优化，去除冗余计算，并利用FPGA的硬件特性（如流水线结构、查找表等）进行加速。
3.坐标变换：
由于畸变矫正需要对每个像素进行几何变换，因此需要设计适合FPGA的坐标变换模块。常用的方法是通过查找表（LUT）加速计算。
4.流水线和时序设计：
需要设计有效的流水线结构，确保在时序上能够处理高速的图像数据流。
FPGA实现的基本步骤：
1.图像输入和输出：
通过HDMI、CameraLink等接口获取图像，并通过显示器或外部设备输出处理结果。
2.畸变矫正模块：
将径向和切向畸变的模型映射到硬件中，利用查找表（LUT）和并行计算优化畸变参数的计算。
3.硬件资源优化：
通过FPGA的资源管理，使用乘法器、加法器等硬件单元对每个像素进行实时计算。
4.实时处理：
对每一帧图像进行实时矫正，保证高帧率输出。
二、MATLAB具体实现
matlab主要是计算逆向映射表，生成fpga使用的而查找表，核心代码如下：
% 读取畸变图像
img = imread('distorted_image.jpg');
[height, width, ~] = size(img);
% 相机标定参数：焦距和图像中心
f_x = 1000; % 水平焦距
f_y = 1000; % 垂直焦距
cx = width / 2; % 水平主点
cy = height / 2; % 垂直主点
% 畸变系数（径向和切向畸变系数）
k1 = -0.2; % 径向畸变系数
k2 = 0.03;
p1 = 0.001; % 切向畸变系数
p2 = -0.001;
% 创建一个空的矫正图像
undistorted_img = zeros(height, width, 3, 'uint8');
% 遍历每个像素点
for i = 1:height
for j = 1:width
% 计算像素点到图像中心的距离
x = j - cx;
y = i - cy;
% 转换到相机坐标系（单位：像素）
x_normalized = x / f_x;
y_normalized = y / f_y;
r = sqrt(x_normalized^2 + y_normalized^2);
% 计算径向畸变
radial_distortion = 1 + k1 * r^2 + k2 * r^4;
% 计算切向畸变
tangential_distortion_x = 2 * p1 * x_normalized * y_normalized + p2 * (r^2 + 2 * x_normalized^2);
tangential_distortion_y = p1 * (r^2 + 2 * y_normalized^2) + 2 * p2 * x_normalized * y_normalized;
% 计算畸变后的坐标（相机坐标系）
x_prime_normalized = x_normalized * radial_distortion + tangential_distortion_x;
y_prime_normalized = y_normalized * radial_distortion + tangential_distortion_y;
% 转换回像素坐标系
x_prime = x_prime_normalized * f_x + cx;
y_prime = y_prime_normalized * f_y + cy;
% 将畸变后的坐标转换为图像坐标系中的整数值
x_prime_img = round(x_prime);
y_prime_img = round(y_prime);
% 检查坐标是否在图像范围内
if x_prime_img >= 1 && x_prime_img <= width && y_prime_img >= 1 && y_prime_img <= height
% 将畸变后的图像像素值赋给新的图像
undistorted_img(y_prime_img, x_prime_img, :) = img(i, j, :);
end
end
end
% 显示矫正后的图像
imshow(undistorted_img);代码中：
fx和fy是水平方向和垂直方向的焦距（通常情况下 fx=fy=f 但并非总是如此）。
cx和cy是图像的主点（即图像中心）。
焦距引入：将焦距 𝑓𝑥 和 𝑓𝑦引入到代码中，确保坐标的转换考虑了图像的内参。
坐标归一化：在畸变模型中，我们将像素坐标归一化为相机坐标系中的单位坐标，通过焦距进行转换。这样可以确保畸变矫正时，图像坐标和物理焦距之间的一致性。
反向映射：矫正后的坐标从归一化坐标系重新映射回像素坐标系。
三、FPGA实现
（一）流程
FPGA因其并行处理和流水线能力，非常适合用于需要高帧率、低延迟的实时校正系统。其实现思路与MATLAB仿真有显著差异，核心挑战在于如何在有限的硬件资源内高效完成映射和插值。
关键技术：逆向映射与查找表（LUT）压缩
在硬件中直接计算每个像素的映射关系非常耗时。因此，常见的优化策略是预先在MATLAB中计算好所有坐标的映射关系，生成一个"逆向映射表"，并将其存储在FPGA的片上存储器（ROM）中。工作时，FPGA只需根据当前像素坐标查找该表，即可获得其在原图中的对应坐标，然后进行插值。
挑战：高清图像的映射表非常大，可能超出片上ROM容量。
解决方案：采用压缩查找表技术。例如，只稀疏地存储部分网格点的映射值，在实际运行时，通过简单的线性插值电路在线快速重建出任意像素的完整映射坐标，从而大幅减少存储需求。
流水线架构设计：
典型的FPGA校正流水线模块包括：图像缓存（如FIFO）、坐标生成器、映射表查找与插值、像素插值计算、输出同步等。这种设计可以让多个像素同时在不同阶段被处理，实现高速数据吞吐。
（二）FPGA优化的关键技术
1.稀疏网格存储：只存储网格点，运行时插值，极大减少存储需求
2.定点量化：将浮点数转换为定点数，适合FPGA处理
3.MIF格式输出：直接生成FPGA ROM初始化文件
（三）映射表压缩效果示例
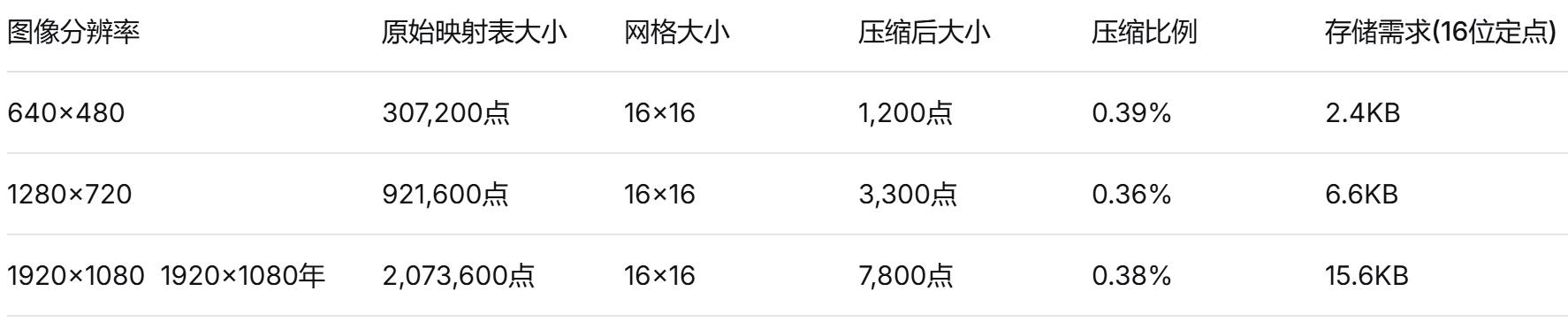
（四）存储优化方案对比
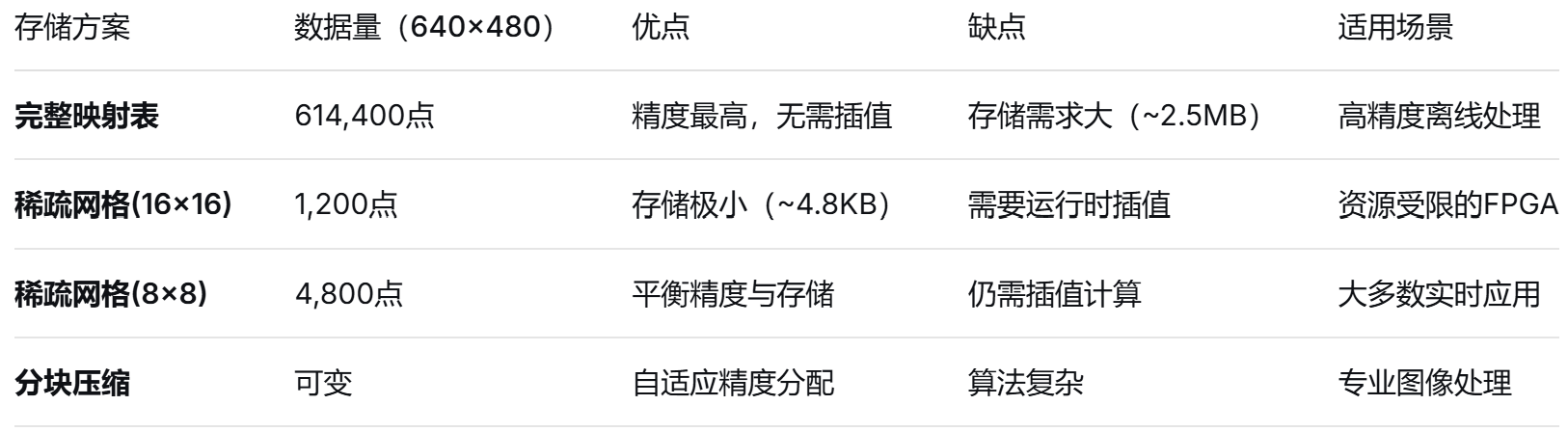
注意：（a）精度平衡：网格大小建议8×8到32×32之间，测试不同值对图像质量的影响；（b）FPGA实现：在FPGA中实现双线性插值来重建完整映射；（c）实时更新：如果畸变参数可能变化，考虑将映射表存储在可重配置的RAM中。
（五）FPGA核心代码及仿真
always@(posedge clk)
begin
if(rst)
begin
status <= IDLE;
ena_odd <= 0;
wea_odd <= 0;
addra_odd <= 16'hffff;
dina_odd <= 0;
enb_odd <= 0;
web_odd <= 0;
addrb_odd <= 16'hffff;
dinb_odd <= 0;
ena_eve <= 0;
wea_eve <= 0;
addra_eve <= 16'hffff;
dina_eve <= 0;
enb_eve <= 0;
web_eve <= 0;
addrb_eve <= 16'hffff;
dinb_eve <= 0;
//ena_x <= 0;
addra_x <= 17'h1ffff;
//ena_y <= 0;
addra_y <= 17'h1ffff;
end
else
begin
case(status)
IDLE:
begin
if(write_str)
begin
status <= WRITE;
if(row[0]==0)//从第0行开始，0行为偶数
begin
ena_odd <= 0;
wea_odd <= 0;
addra_odd <= 16'hffff;
dina_odd <= 0;
ena_eve <= 1;
wea_eve <= 1;
addra_eve <= ((row>>1)<<8) + ((row>>1)<<6) + col;
dina_eve <= din_d1;
end
else
begin
ena_odd <= 1;
wea_odd <= 1;
addra_odd <= (((row-1)>>1)<<8) + (((row-1)>>1)<<6) + col;
dina_odd <= din_d1;
ena_eve <= 0;
wea_eve <= 0;
addra_eve <= 16'hffff;
dina_eve <= 0;
end
end
else
begin
status <= IDLE;
ena_odd <= 0;
wea_odd <= 0;
addra_odd <= 16'hffff;
dina_odd <= 0;
enb_odd <= 0;
web_odd <= 0;
addrb_odd <= 16'hffff;
dinb_odd <= 0;
ena_eve <= 0;
wea_eve <= 0;
addra_eve <= 16'hffff;
dina_eve <= 0;
enb_eve <= 0;
web_eve <= 0;
addrb_eve <= 16'hffff;
dinb_eve <= 0;
//ena_x <= 0;
addra_x <= 17'h1ffff;
//ena_y <= 0;
addra_y <= 17'h1ffff;
end
end
WRITE:
begin
if(write_end)
begin
status <= DELAY;
ena_odd <= 0;
wea_odd <= 0;
addra_odd <= 16'hffff;
dina_odd <= 0;
ena_eve <= 0;
wea_eve <= 0;
addra_eve <= 16'hffff;
dina_eve <= 0;
end
else
begin
status <= WRITE;
if(row[0]==0)//从第0行开始，0行为偶数
begin
ena_odd <= 0;
wea_odd <= 0;
addra_odd <= 16'hffff;
dina_odd <= 0;
ena_eve <= 1;
wea_eve <= 1;
addra_eve <= ((row>>1)<<8) + ((row>>1)<<6) + col;
dina_eve <= din_d1;
end
else
begin
ena_odd <= 1;
wea_odd <= 1;
addra_odd <= (((row-1)>>1)<<8) + (((row-1)>>1)<<6) + col;
dina_odd <= din_d1;
ena_eve <= 0;
wea_eve <= 0;
addra_eve <= 16'hffff;
dina_eve <= 0;
end
end
end
DELAY:
begin
if(dly_cnt == 32)
begin
status <= READ;
dly_cnt <= 0;
end
else
begin
status <= DELAY;
dly_cnt <= dly_cnt + 1;
end
end
/* begin
if(dly_cnt == 32)
begin
status <= READ;
dly_cnt <= 0;
ena_odd <= 0;
end
//else if(dly_cnt == 5 || dly_cnt == 6)
else if(dly_cnt == 5)
begin
status <= DELAY;
dly_cnt <= dly_cnt + 1;
ena_odd <= 1;
wea_odd <= 0;
addra_odd <= 96;
end
else
begin
status <= DELAY;
dly_cnt <= dly_cnt + 1;
ena_odd <= 0;
end
end */
READ:
begin
if((row_rd == 10'd255) && (col_rd == 319))
begin
status <= DELAY1;
col_rd <= col_rd;
row_rd <= row_rd;
end
else
begin
status <= READ;
if(col_rd == 319)
begin
row_rd <= row_rd + 1;
col_rd <= 0;
end
else
begin
row_rd <= row_rd;
col_rd <= col_rd + 1;
end
end
if(v1[0] == 0)
begin
ena_odd <= 1;
wea_odd <= 0;
addra_odd <= ((((v2>>6)-1)>>1)<<8) + ((((v2>>6)-1)>>1)<<6) + (u1>>6);
enb_odd <= 1;
web_odd <= 0;
addrb_odd <= ((((v2>>6)-1)>>1)<<8) + ((((v2>>6)-1)>>1)<<6) + (u2>>6);
ena_eve <= 1;
wea_eve <= 0;
addra_eve <= (((v1>>6)>>1)<<8) + (((v1>>6)>>1)<<6) + (u1>>6);
enb_eve <= 1;
web_eve <= 0;
addrb_eve <= (((v1>>6)>>1)<<8) + (((v1>>6)>>1)<<6) + (u2>>6);
end
else
begin
if(v1 == 16320)//255<<6
begin
ena_odd <= 1;
wea_odd <= 0;
addra_odd <= ((((v1>>6)-1)>>1)<<8) + ((((v1>>6)-1)>>1)<<6) + (u1>>6);
enb_odd <= 1;
web_odd <= 0;
addrb_odd <= ((((v1>>6)-1)>>1)<<8) + ((((v1>>6)-1)>>1)<<6) + (u2>>6);
ena_eve <= 1;
wea_eve <= 0;
addra_eve <= ((((v2>>6)-1)>>1)<<8) + ((((v2>>6)-1)>>1)<<6) + (u1>>6);
enb_eve <= 1;
web_eve <= 0;
addrb_eve <= ((((v2>>6)-1)>>1)<<8) + ((((v2>>6)-1)>>1)<<6) + (u2>>6);
end
else
begin
ena_odd <= 1;
wea_odd <= 0;
addra_odd <= ((((v1>>6)-1)>>1)<<8) + ((((v1>>6)-1)>>1)<<6) + (u1>>6);
enb_odd <= 1;
web_odd <= 0;
addrb_odd <= ((((v1>>6)-1)>>1)<<8) + ((((v1>>6)-1)>>1)<<6) + (u2>>6);
ena_eve <= 1;
wea_eve <= 0;
addra_eve <= (((v2>>6)>>1)<<8) + (((v2>>6)>>1)<<6) + (u1>>6);
enb_eve <= 1;
web_eve <= 0;
addrb_eve <= (((v2>>6)>>1)<<8) + (((v2>>6)>>1)<<6) + (u2>>6);
end
end
//ena_x <= 1;
addra_x <= (row_rd<<8) + (row_rd<<6) + col_rd;
//ena_y <= 1;
addra_y <= (row_rd<<8) + (row_rd<<6) + col_rd;
end
DELAY1:
begin
if(dly_cnt1 == 32)
begin
status <= IDLE;
dly_cnt1<= 0;
col_rd <= 0;
row_rd <= 0;
ena_odd <= 0;
wea_odd <= 0;
addra_odd <= 16'hffff;
dina_odd <= 0;
enb_odd <= 0;
web_odd <= 0;
addrb_odd <= 16'hffff;
dinb_odd <= 0;
ena_eve <= 0;
wea_eve <= 0;
addra_eve <= 16'hffff;
dina_eve <= 0;
enb_eve <= 0;
web_eve <= 0;
addrb_eve <= 16'hffff;
dinb_eve <= 0;
//ena_x <= 0;
addra_x <= 17'h1ffff;
//ena_y <= 0;
addra_y <= 17'h1ffff;
end
else
begin
status <= DELAY1;
dly_cnt1<= dly_cnt1 + 1;
col_rd <= col_rd;
row_rd <= row_rd;
if(v1[0] == 0)
begin
ena_odd <= 1;
wea_odd <= 0;
addra_odd <= ((((v2>>6)-1)>>1)<<8) + ((((v2>>6)-1)>>1)<<6) + (u1>>6);
enb_odd <= 1;
web_odd <= 0;
addrb_odd <= ((((v2>>6)-1)>>1)<<8) + ((((v2>>6)-1)>>1)<<6) + (u2>>6);
ena_eve <= 1;
wea_eve <= 0;
addra_eve <= (((v1>>6)>>1)<<8) + (((v1>>6)>>1)<<6) + (u1>>6);
enb_eve <= 1;
web_eve <= 0;
addrb_eve <= (((v1>>6)>>1)<<8) + (((v1>>6)>>1)<<6) + (u2>>6);
end
else
begin
if(v1 == 16320)//255<<6
begin
ena_odd <= 1;
wea_odd <= 0;
addra_odd <= ((((v1>>6)-1)>>1)<<8) + ((((v1>>6)-1)>>1)<<6) + (u1>>6);
enb_odd <= 1;
web_odd <= 0;
addrb_odd <= ((((v1>>6)-1)>>1)<<8) + ((((v1>>6)-1)>>1)<<6) + (u2>>6);
ena_eve <= 1;
wea_eve <= 0;
addra_eve <= ((((v2>>6)-1)>>1)<<8) + ((((v2>>6)-1)>>1)<<6) + (u1>>6);
enb_eve <= 1;
web_eve <= 0;
addrb_eve <= ((((v2>>6)-1)>>1)<<8) + ((((v2>>6)-1)>>1)<<6) + (u2>>6);
end
else
begin
ena_odd <= 1;
wea_odd <= 0;
addra_odd <= ((((v1>>6)-1)>>1)<<8) + ((((v1>>6)-1)>>1)<<6) + (u1>>6);
enb_odd <= 1;
web_odd <= 0;
addrb_odd <= ((((v1>>6)-1)>>1)<<8) + ((((v1>>6)-1)>>1)<<6) + (u2>>6);
ena_eve <= 1;
wea_eve <= 0;
addra_eve <= (((v2>>6)>>1)<<8) + (((v2>>6)>>1)<<6) + (u1>>6);
enb_eve <= 1;
web_eve <= 0;
addrb_eve <= (((v2>>6)>>1)<<8) + (((v2>>6)>>1)<<6) + (u2>>6);
end
end
// ena_x <= 0;
// addra_x <= 17'h1ffff;
// ena_y <= 0;
// addra_y <= 17'h1ffff;
//ena_x <= 1;
addra_x <= (row_rd<<8) + (row_rd<<6) + col_rd;
//ena_y <= 1;
addra_y <= (row_rd<<8) + (row_rd<<6) + col_rd;
end
end
default:
begin
end
endcase
end
end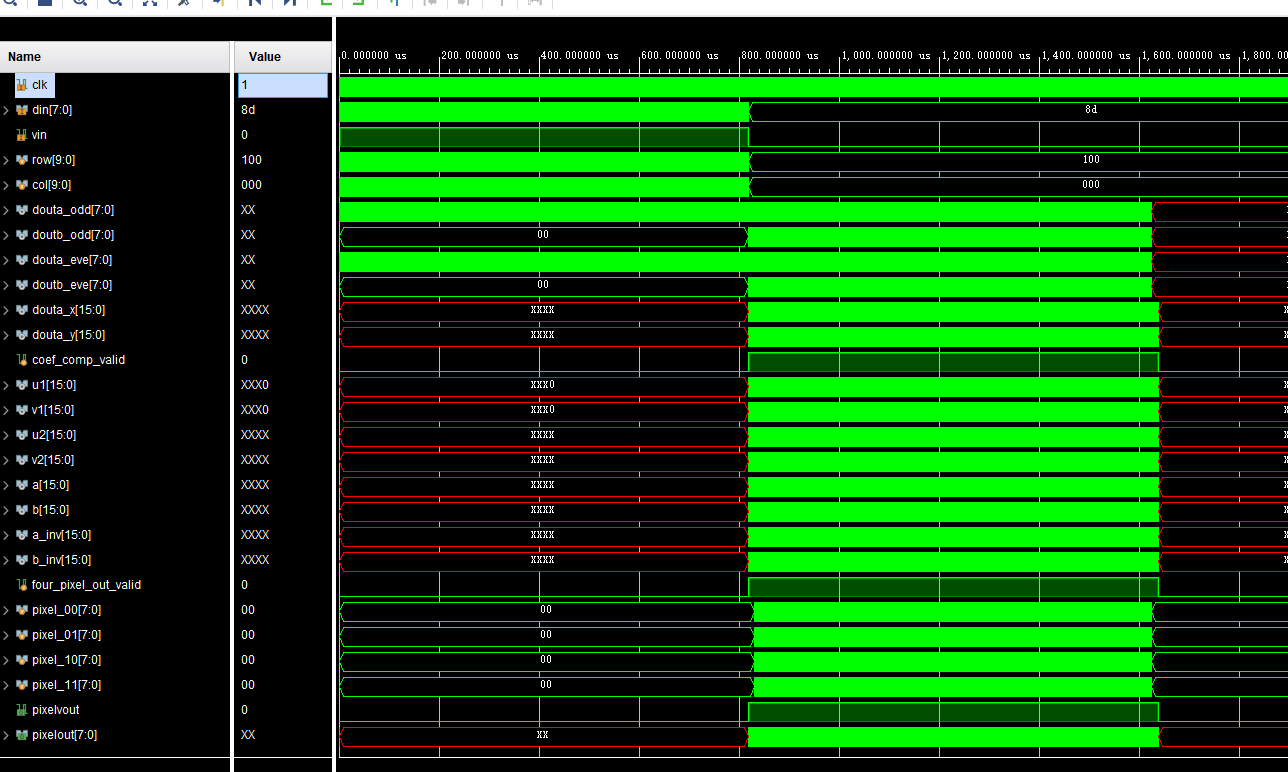
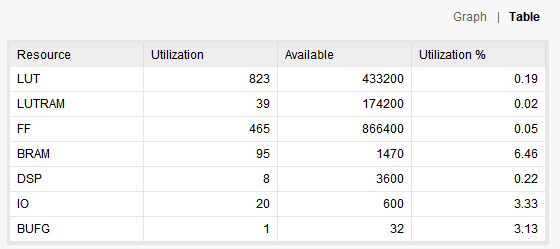
（六）资源分析
四、结果分析
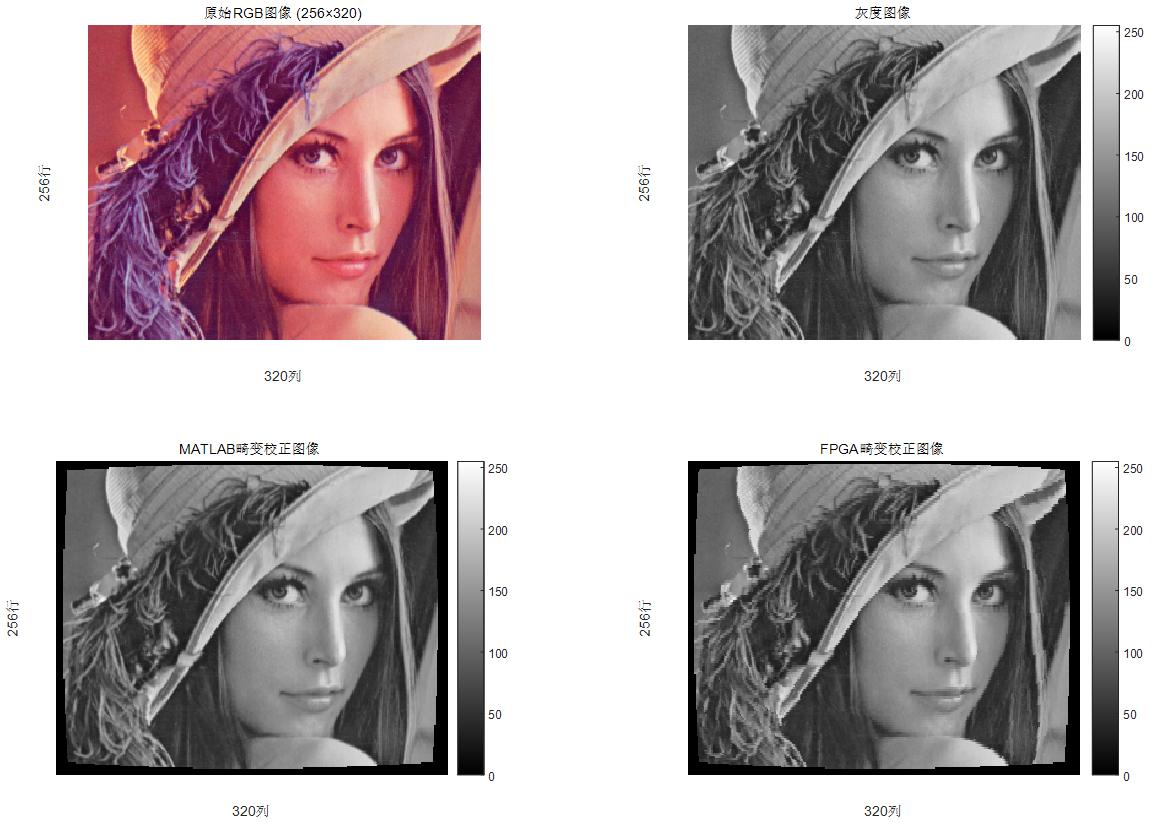
上图是matlab与fpga实现结果的比较分析，结果还算可以，在fpga实现过程中，将原始图所有像素都缓存了，并没有考虑使用稀疏网格存储，后面有时间再验证一下。
五、扩展
（一）焦距（像素单位）到底是什么
在图像处理和计算机视觉中，fx 和 fy 是将真实世界的物理距离（毫米）转换为图像平面上的像素距离的缩放因子，通常被称为相机的焦距（以像素为单位）。
为了帮你更清晰地理解它与我们日常所说的物理焦距的区别，可以看下面的对比：
（1）像素焦距的计算与作用
像素焦距可以通过以下公式与物理焦距关联：
fx = (物理焦距f / 传感器像素尺寸dx)
fy = (物理焦距f / 传感器像素尺寸dy)
例如，一个焦距8mm的镜头，搭配一个每个像素大小为0.004mm的传感器，那么 fx = fy = 8 / 0.004 = 2000 像素。
在你使用的畸变矫正代码中，fx 和 fy 是相机内参矩阵的核心部分，其作用至关重要：
建立映射关系：在"归一化平面坐标 -> 像素坐标"的转换中，它们是将计算出的理论坐标"放大"到实际图像尺寸的关键一步（公式：u = x_norm * fx + cx）。
影响校正效果：如果 fx, fy 的值设置得与实际相机参数偏差很大，会导致映射计算错误，从而可能引起图像被过度拉伸、压缩或出现我们之前讨论的严重裁剪问题。
（2）如何确认
在你的代码里，fx = fy = 1000 是一个假设的、用于示例的简化值。它通常对应一种近似情况：假设相机传感器和镜头是理想的，且图像的主点 (cx, cy) 正好在图像中心。
在实际应用中，你必须使用自己相机的真实标定参数来替换这些值！ 获取方法通常有两种：
相机标定：使用MATLAB的 Camera Calibrator 工具箱或OpenCV等工具，通过拍摄多张标准棋盘格标定板图像，可以高精度地计算出 fx, fy, cx, cy 以及畸变系数 k1, k2, p1, p2 等。
估算：如果无法标定，可根据图像尺寸粗略估算。例如，对于视角约为90度的广角镜头，其焦距 fx 大约等于图像宽度的一半。对于你1280x1707的图像，fx 可能在640-850像素左右。
（3）可忽略fx、fy（归一化）过程吗？
绝对不可以省略 fx 和 fy。 忽略它们，等于彻底破坏了整个畸变校正模型的几何基础，会导致完全错误的校正结果。简单来说，省略 fx 和 fy 后，你执行的将不再是"相机畸变校正"，而是一种无法定义、无物理意义的坐标扭曲。
公式 x_norm = (u - cx) / fx 并非随意设计，它源自最基础的相机针孔模型。这一步"归一化"的目的，是将图像上的像素坐标 (u, v)，转换到以相机光心为原点的、没有单位的物理三维空间坐标系中。
(u - cx)：这一步是将坐标原点从图像左上角移动到图像的主点（通常接近中心）。这解决了"哪里是中心"的问题。
/ fx：这才是关键一步。它通过除以焦距（像素单位），消除了相机传感器尺寸和分辨率带来的影响，得到了点在相机前方单位距离（Z=1）的成像平面上的物理坐标。这个坐标 (x_norm, y_norm) 只与光线的方向有关，与具体的相机型号无关。
（二）与家用投影仪图像校正区别
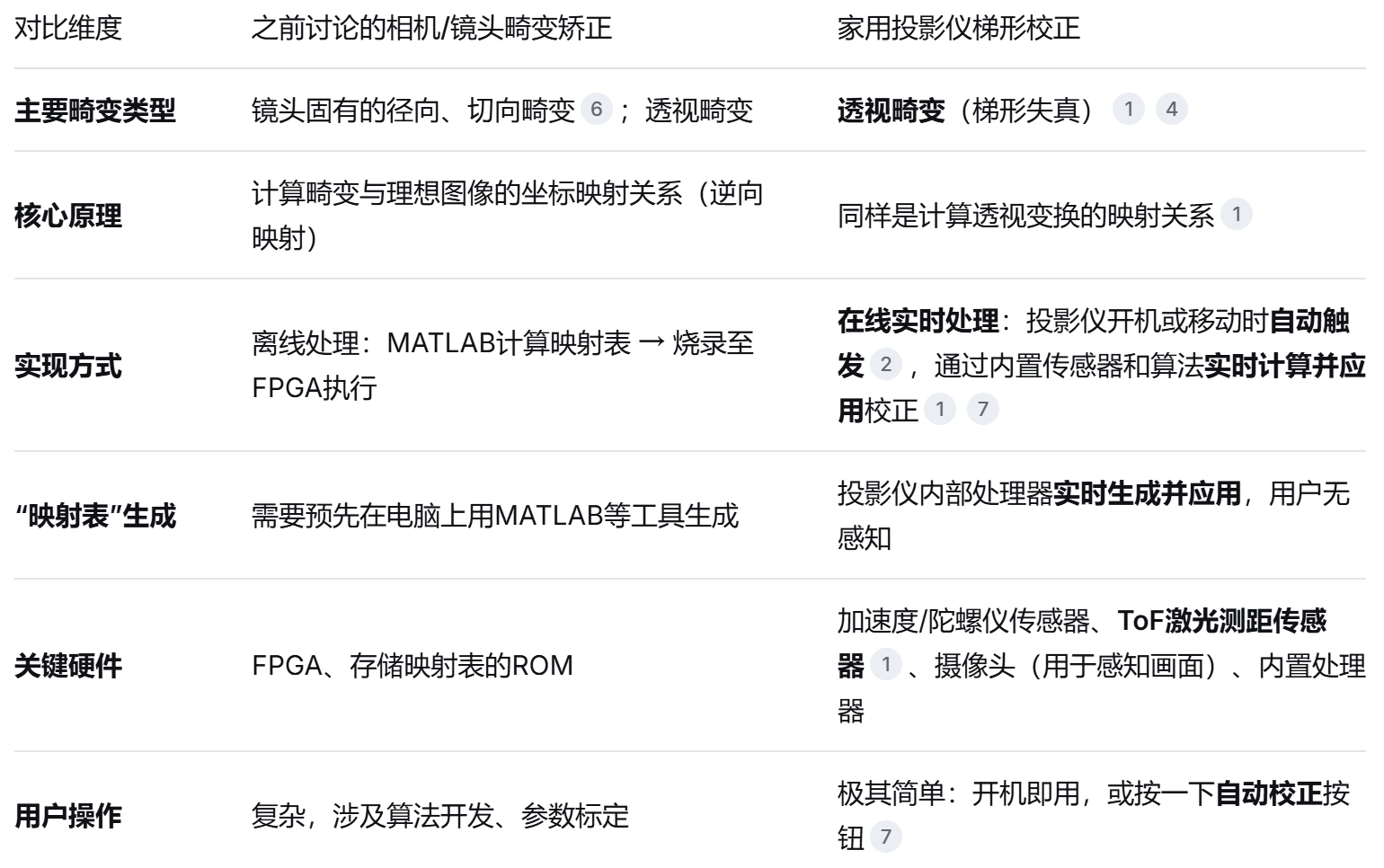
家用投影仪的梯形校正和之前讨论的相机畸变矫正，虽然在几何原理上是一脉相承的（都涉及透视变换），但在实现方式和技术路径上有着显著区别。其核心区别在于，家用投影仪通过高度自动化、实时性的内置系统替代了需要手动操作的离线计算。简单来说，你可以理解为投影仪内置了一个"实时版"的MATLAB校正程序。为了让你快速了解全貌，我将它们的主要区别整理如下：
（三）双线性插值
双线性插值（Bilinear Interpolation）是一种在二维空间中进行插值的方法，用于计算一个点在已知四个邻近点之间的值。它常用于图像处理、计算机图形学等领域，尤其是在缩放和旋转图像时用来估算新的像素值。
假设已知四个邻近点的值（x1, y1）、(x2, y1)、(x1, y2)、(x2, y2) 对应的函数值分别为 f(x1,y1), f(x2,y1), f(x1,y2), f(x2,y2)，那么对于任意一个点 (x,y)，其插值可以通过以下步骤进行：
1.在 x 方向进行线性插值：
对于给定的 y 值，先对 (x1, y1) 和 (x2, y1) 以及 (x1, y2) 和 (x2, y2) 进行线性插值。
计算：
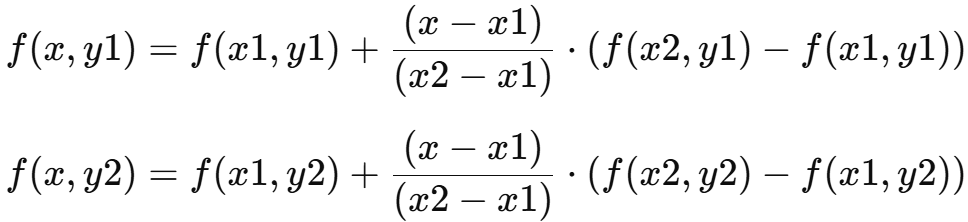
2.在 y 方向进行线性插值：
对于已插值得到的 f(x,y1) 和 f(x,y2)进行线性插值，得到最终的插值结果。
