🎬 胖咕噜的稞达鸭 :个人主页
🔥 个人专栏 : 《数据结构》《C++初阶高阶》
《Linux系统学习》
《算法日记》
⛺️技术的杠杆,撬动整个世界!

🐥位运算常见总结:


本专题的前缀文章:
只出现一次的数字I
算法原理:
将数组中所有元素都异或在一起,除了某个元素只出现一次以外,其余每个元素均出现两次。最终异或的结果就是所求。
cpp
class Solution {
public:
int singleNumber(vector<int>& nums) {
int sum = 0;
for(int num :nums) sum ^= num;
return sum;
}
};只出现一次的数字II
算法原理:位运算
把数组中的数字都放在bit中,有32个位,0 和 1 指的是某个数字的二进制表示中的一位(bit)的值。
3n个0 + singel 0; -----取模 0
3n个0 + singel 1; -----取模 1
3n个1 + singel 0; -----取模 0
3n个1 + singel 1; -----取模 1
对于每一位 i:
- 统计数组中所有数字在该位为 1 的个数(sum)
- 因为除了目标数字外,其他数字都出现 3 次,所以 sum = 3×k + b
- k 是出现 3 次的数字中该位为 1 的个数
- b 是目标数字在该位的值(0 或 1)
sum % 3 = b,所以:- 如果 b = 0 → 目标数字该位为 0
- 如果 b = 1 → 目标数字该位为 1,设置 ret 的该位为 1
这样遍历完 32 位后,ret 就是只出现一次的数字。
cpp
class Solution {
public:
int singleNumber(vector<int>& nums) {
int ret = 0;//用于返回最后的结果
for(int i = 0;i < 32;i++)//修改ret中的值
{
int sum = 0;
for(int x:nums)//遍历nums,计算nums中所有数字的第i位的和
if(((x >> i) & 1) == 1)//此时第i位置的数字为1
sum++;
sum %= 3;//所有出现在nums第0位的数字都加起来,再取模3
if(sum == 1)ret |= (1 << i);//判断如果sum 最后取模等于1,就说明这个数字单独出现过
}
return ret;
}
};只出现一次的数字III
解题原理:
- 所有数异或:
一个数组中只有两个数字只出现了一次,其余都出现了两次,先将数组中所有的数字都进行异或,最后剩下的一个数字就是唯一出现一次的这两个数字的异或和; - 分组:找不同;(找出不同的才可以分组:那干脆去找异或和中的最低位置的1)
先找出这个异或和最低位置的1,定义为diff(一定有1存在)找出这个1所在的编号, - 如果这个编号跟1按位与,最终结果就是1;再跟数组中的其他数字异或,最后可以找出来这个数;
这个编号跟0按位与,最终结果就是0;再跟数组中的其他数字异或,最后可以找出另外一个数字; - 最后返回这两个数字。
cpp
class Solution {
public:
vector<int> singleNumber(vector<int>& nums) {
int tmp = 0;
for(int i:nums)tmp ^= i;//tmp中存储异或和
unsigned int diff = (unsigned int)tmp & -(unsigned int)tmp;
int a = 0,b = 0;
for(int num : nums)
{
if(diff & num)a ^= num;
else b ^= num;
}
return {a,b};
}
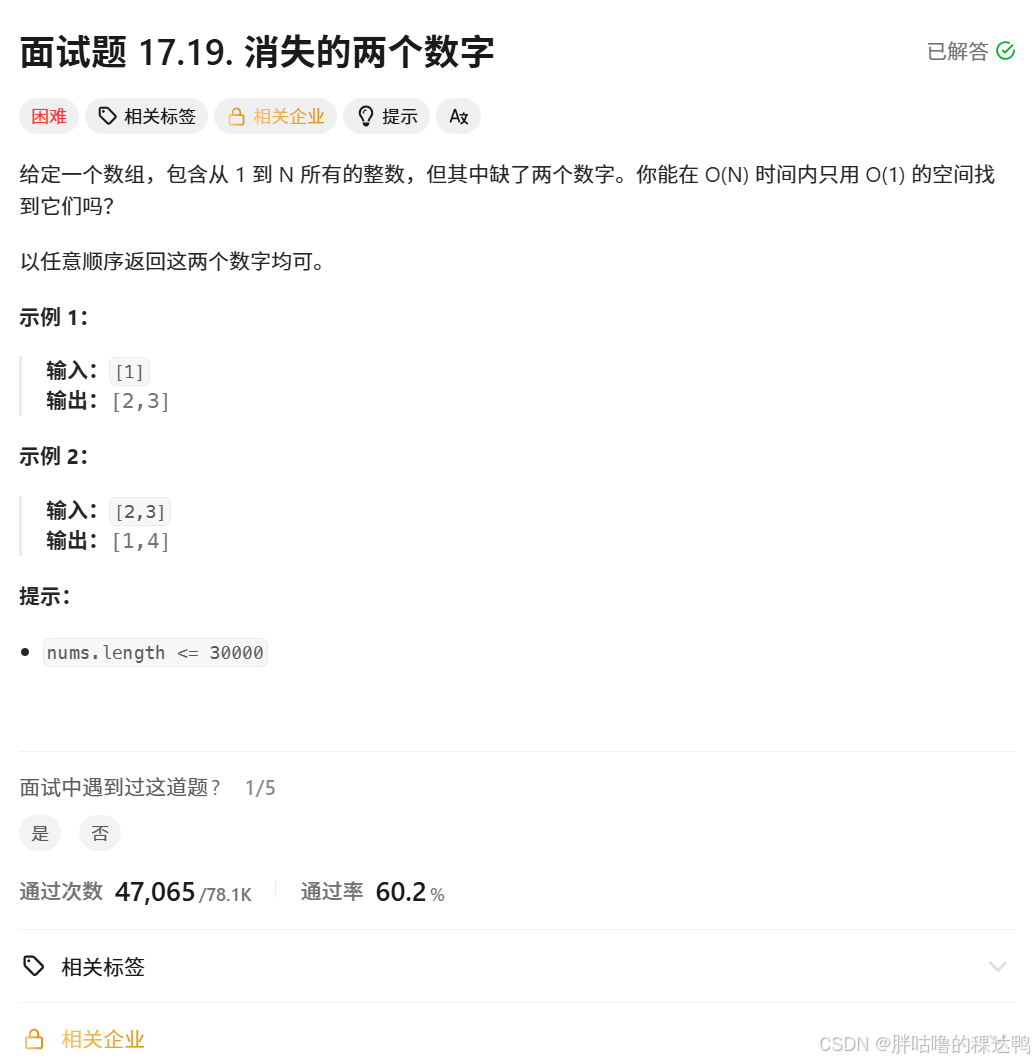
};面试题:消失的两个数字
解法:数组中本身有nums个数字,
这些数字加上消失的两个数字a,b,恰好是1~N中连续的数字区间,
所以nums中数字(缺失数组)+ 这段区间(完整数组) --->构成问题:只出现一次的数字III
关键:其余数字都出现了两次,只有a和b出现了一次,返回a 和 b.
解题:
- 可以将所有的数字异或在一起,将结果收集在tmp中,tmp = a^ b;
- 找到tmp中比特位为1的那一位(异或的时候相同为0相异为1):
- 根据x位的不同,划分为两类异或:
将这个x位置比特位为1的数字,将其其余的数字都跟1异或在一起;(假设是b类)
将这个x位置比特位为0的数字,将其其余的数字都跟0异或在一起;(假设是a类)
注意:这个其余的数字,既要在完整数组中进行异或操作,也要在缺失数组中进行异或。
其余数字都出现过两次,只有其中一位数字只出现了一次;
cpp
class Solution {
public:
vector<int> missingTwo(vector<int>& nums) {
int tmp = 0;
for(int i =1;i<=nums.size()+2;i++)tmp^=i;
for(int num: nums)tmp^=num;
//找出ab比特位中不同的那一位
int diff = 0;
while(1)
{
if(((tmp >> diff) &1)==1)break;
else diff++;
}
//根据diff的不同,将所有的数字都划分为两类来进行异或
int a = 0,b = 0;
for(int num: nums)
if(((num >> diff) & 1) == 1)b^= num;
else a ^= num;
for(int i = 1;i<= nums.size()+2;i++)
if(((i >> diff) & 1) == 1) b^= i;
else a ^= i;
return {a,b};
}
};方法二:位运算:取最低位次的1
cpp
class Solution {
public:
vector<int> missingTwo(vector<int>& nums) {
int sum = 0;
for(int i = 1;i <= nums.size()+2; i++)sum ^= i;
for(int num :nums)sum ^= num;
int lowbit = sum & -sum;//取出最低位置的1在哪一位,如果是倒数第二位就是2,倒数第三位就是3,是一个编号
int a = 0,b= 0;
for(int i = 1; i<= nums.size()+2;i++)
{
if(i & lowbit)a ^= i;//判断这个位置的数字和i按位与,如果i是0,按位与的结果是0;
else b ^= i;//如果按位与的结果是1,最终要按照lowbit算,取编号
}
for(int num :nums)
{
if(num & lowbit) a ^= num;
else b ^= num;
}
return {a,b};
}
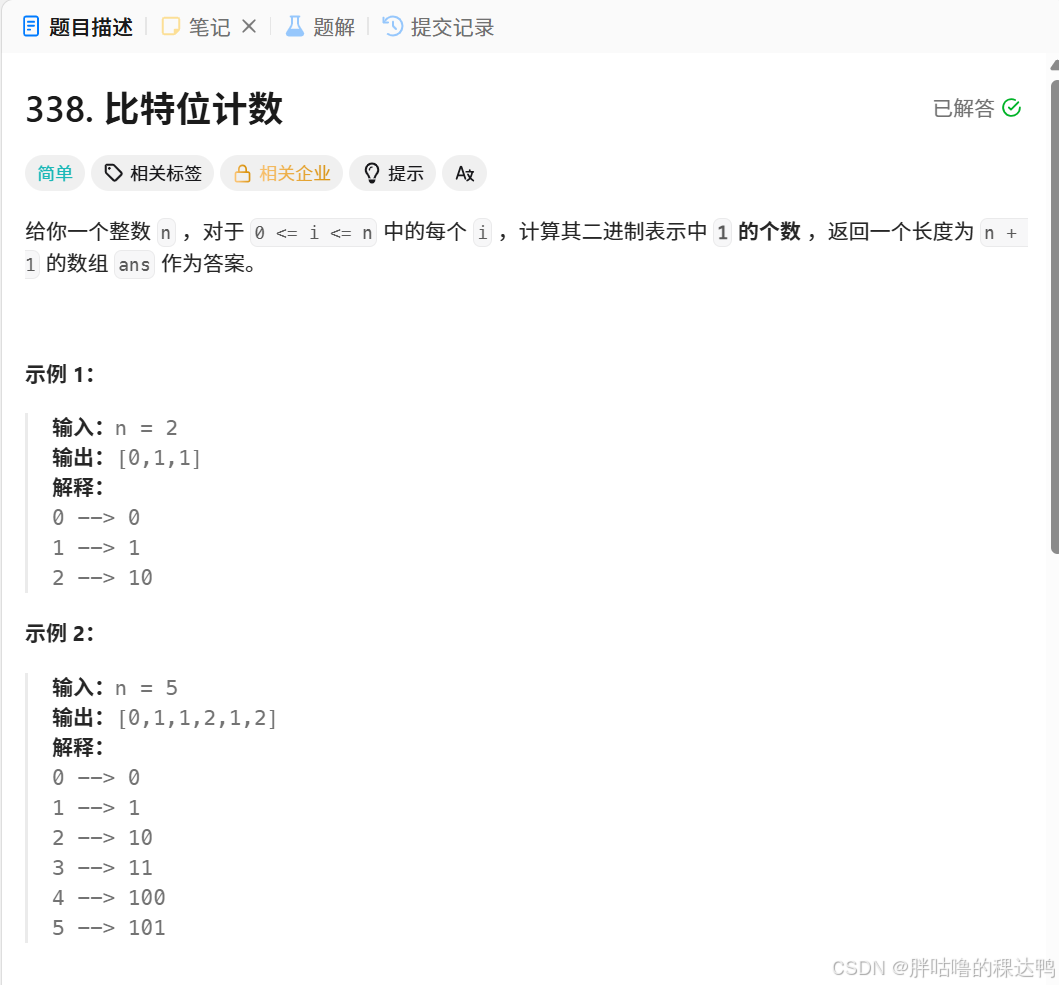
};比特位计数
题目解析 :
对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
思路:
找出0 <= i <= n中每一个数字二进制表示中总共有几个1,数组中表示的是每一个i位有几个1;将每一个数字放到位图中,每一位为1,sum ++,一个数字放好到位图中之后返回sum。
ret[x]中收集每一个countBit中返回的sum个数,sum用来计数字1.
cpp
class Solution {
public:
vector<int> countBits(int n) {
vector<int>ret(n+1);//用于返回最终结果的ret有n+1个空间,第n个数字二进制中有几个1也要返回
auto countBit = [](int x)
{
int sum = 0;
for(int i =0 ;i<32;i++)
{
if((x >> i) & 1 ) sum++;//将x右移动i位,并且按位与1判断它的第i个位置是1还是0,如果是1就sum++
}
return sum;//返回这个数字的二进制数有多少个1
};//多次调用countBit(x) 函数计算 x 的二进制中 1 的个数
for(int x = 0;x<=n;x++)
{
ret[x] = countBit(x);//将结果存储在数组 ret 的第 x 个位置
}
return ret;
}
};通过这道题我们可以总结出:(x >> i) & 1的操作适用于以下情景:
- 判断n的第i位是0还是1:
cpp
if((n >> i) & 1)- 统计二进制中1的个数:
cpp
int countBits(int x)
{
int sum = 0;
for(int i = 0;i < 32; i++)
{
if((x >> i) & 1)sum++;//x不断右移动i个位置,跟1按位与
}
return sum;
}示例:
int x = 13; // 二进制:1101
int sum = 0;
int i = 0;
// 检查第0位
if((13 >> 0) & 1) sum++; // (1101 & 1) = 1,sum变为1
// 检查第1位
if((13 >> 1) & 1) sum++; // (0110 & 1) = 0,sum不变
// 检查第2位
if((13 >> 2) & 1) sum++; // (0011 & 1) = 1,sum变为2
// 检查第3位
if((13 >> 3) & 1) sum++; // (0001 & 1) = 1,sum变为3
所以13的二进制表达中有3个1.