从0开始学算法——第二十一天（高级链表操作）

写在开头的话

从今天开始让我们一起来学习链表的相关知识吧。不过这块知识比较多，我会分成三部分来写。现在开始今天的第二部分------高级链表操作吧。

第一节

在计算机科学中，整数的表示受限于系统的位数。对于超过系统最大整数表示范围的"大数"，传统的数据类型无法处理，因此需要使用特定的数据结构和算法来实现大数运算。链表作为一种灵活的动态数据结构，非常适合进行大数运算，尤其是对于那些需要逐位操作的大数。链表能够高效地处理任意长度的数字并支持多种大数运算操作，例如加法、减法、乘法等。

知识点：

（1）链表表示大数加法（2）链表表示大数乘法

链表表示大数加法

Leetcode-两数之和2

题目描述

给你两个 非空 链表来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储一位数字。将这两数相加会返回一个新的链表。

你可以假设除了数字 0 之外，这两个数字都不会以零开头。

解法

我们可以使用栈来存储链表中的元素。

遍历链表时，将每个节点的值依次压入栈中，这样，两个链表的数位就会对齐，并且位于栈顶。接着，利用栈的先进后出特性，从最低位开始依次计算两个数位的和，同时注意处理进位的情况。

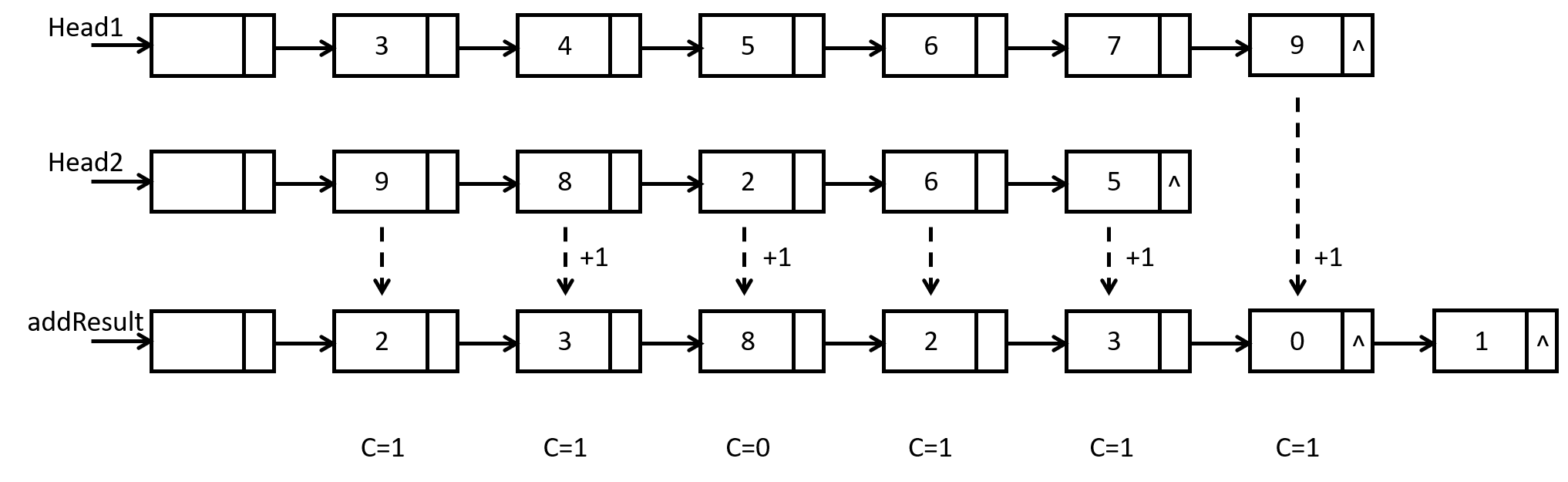
图示

下图是：976543+56289 的结果，在头结点对齐。

代码实现

C++代码实现

class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        stack<int> s1, s2;
        while (l1) {
            s1.push(l1 -> val);
            l1 = l1 -> next;
        }
        while (l2) {
            s2.push(l2 -> val);
            l2 = l2 -> next;
        }
        int carry = 0;
        ListNode* ans = nullptr;
        while (!s1.empty() or !s2.empty() or carry != 0) {
            int a = s1.empty() ? 0 : s1.top();
            int b = s2.empty() ? 0 : s2.top();
            if (!s1.empty()) s1.pop();
            if (!s2.empty()) s2.pop();
            int cur = a + b + carry;
            carry = cur / 10;
            cur %= 10;
            auto curnode = new ListNode(cur);
            curnode -> next = ans;
            ans = curnode;
        }
        return ans;
    }
};

Java代码实现

class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        Deque<Integer> stack1 = new ArrayDeque<Integer>();
        Deque<Integer> stack2 = new ArrayDeque<Integer>();
        while (l1 != null) {
            stack1.push(l1.val);
            l1 = l1.next;
        }
        while (l2 != null) {
            stack2.push(l2.val);
            l2 = l2.next;
        }
        int carry = 0;
        ListNode ans = null;
        while (!stack1.isEmpty() || !stack2.isEmpty() || carry != 0) {
            int a = stack1.isEmpty() ? 0 : stack1.pop();
            int b = stack2.isEmpty() ? 0 : stack2.pop();
            int cur = a + b + carry;
            carry = cur / 10;
            cur %= 10;
            ListNode curnode = new ListNode(cur);
            curnode.next = ans;
            ans = curnode;
        }
        return ans;
    }
}

Python代码实现

class Solution:
    def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:
        s1, s2 = [], []
        while l1:
            s1.append(l1.val)
            l1 = l1.next
        while l2:
            s2.append(l2.val)
            l2 = l2.next
        ans = None
        carry = 0
        while s1 or s2 or carry != 0:
            a = 0 if not s1 else s1.pop()
            b = 0 if not s2 else s2.pop()
            cur = a + b + carry
            carry = cur // 10
            cur %= 10
            curnode = ListNode(cur)
            curnode.next = ans
            ans = curnode
        return ans

代码讲解

这段代码的目的是用链表表示的两个大数相加。由于链表是按照从高位到低位的顺序存储的，因此加法需要从最低位（即尾部）开始进行计算。为了实现从尾部开始相加，代码使用了栈的数据结构来帮助反转链表的遍历顺序。下面具体讲解代码的工作原理：

原理讲解

1. 链表节点的反转存储：

   • 首先，代码将两个链表 l1 和 l2 中的每个节点的值依次压入两个栈 s1 和 s2。由于栈的"后进先出"特性，链表的最后一个节点（最低位）会被第一个取出，从而可以实现从低位到高位的加法运算。

2. 逐位相加：

   • 利用两个栈分别存储的链表节点值，逐位从栈顶取出数字，进行加法运算。为了处理加法中的进位，使用了一个变量 carry 来记录是否需要进位。
   • 每次将栈 s1 和 s2 的栈顶元素取出相加，若栈为空则默认取 0，计算后将进位和当前位的结果分别存储。
   • 当前位的值取余 10 得到，并将新的链表节点插入到结果链表的最前面，模拟逐位向前构建链表。

3. 处理进位：

   • 如果在最后两条链表的所有位都加完了，但仍有进位未处理（carry != 0），还需要再构建一个新的节点存储进位值。

4. 链表的构建：

   • 使用一个新的链表 ans 来存储加法的结果，每次计算完一位后，将该位结果节点插入到链表头部。
   • 最终构建好的链表 ans 即为两个数相加的结果。

主要步骤

1. 将链表 l1 和 l2 中的所有节点值依次压入栈 s1 和 s2。
2. 使用 carry 记录进位，逐位弹出栈顶元素进行相加。
3. 每次相加后的结果作为新节点插入到结果链表的头部。
4. 最后返回结果链表 ans，代表两个大数相加的结果。

复杂度分析

• 时间复杂度 ：O(n)，其中 n 是链表的长度。每个链表中的节点最多只会被遍历两次，一次是压入栈，另一次是弹出栈。
• 空间复杂度：O(n)，栈的大小和链表的节点数成正比。

示例：

假设 l1 = 7 -> 2 -> 4 -> 3，l2 = 5 -> 6 -> 4，表示的数字分别为 7243 和 564。

• 首先将 l1 和 l2 的节点依次压入栈中：

  • s1 = [7, 2, 4, 3]
  • s2 = [5, 6, 4]

• 逐位相加：

  • 3 + 4 = 7，carry = 0，当前链表为 7 -> NULL
  • 4 + 6 = 10，carry = 1，当前链表为 0 -> 7 -> NULL
  • 2 + 5 + 1(进位) = 8，carry = 0，当前链表为 8 -> 0 -> 7 -> NULL
  • 7 + 0 = 7，carry = 0，当前链表为 7 -> 8 -> 0 -> 7 -> NULL

最终结果链表为 7 -> 8 -> 0 -> 7，表示的数字是 7807，即为 7243 + 564 的结果。

链表表示大数乘法

思路讲解

• 考虑链表的数据结构：先思考，链表结点要有 pre、next 指针，所以是双向链表，要设置头尾节点。这里让尾结点指向最后一个结点，头节点为虚结点。

• 链表构造问题：从输入的字符串转换为整型的链表

• 相乘：为了错位相加中运算方便，我将结果倒序表示，头节点后面连结果的最后一位数。一开始结果链表 result 为空，所以创建结点；用2个结点指针控制错位相加，注意进位的问题，在两个地方可能会进位：乘法运算并加上进位得到结果时和错位相加时。

代码实现

C++代码实现

#include <iostream>
#include <string>
using namespace std;

class BigIntNode {
public:
    int data;
    BigIntNode* pre;
    BigIntNode* next;
    BigIntNode() : data(0), pre(nullptr), next(nullptr) {}
    ~BigIntNode() {}
};

class BigInt {
public:
    BigIntNode* head;
    BigIntNode* rear;
    
    BigInt() {
        head = new BigIntNode(); // 虚的
        rear = head; // 指向最后一个
    }

    ~BigInt() {
        BigIntNode* tmp = head;
        while (tmp) {
            BigIntNode* nextNode = tmp->next;
            delete tmp;
            tmp = nextNode;
        }
    }

    void create(const string& a) { // 尾插
        const char* b = a.c_str();
        for (int i = 0; i < a.length(); i++) {
            BigIntNode* newNode = new BigIntNode();
            newNode->data = b[i] - '0';
            newNode->pre = rear;
            newNode->next = NULL;
            rear->next = newNode;
            rear = newNode;
        }
    }

    void create(int a) { // 插入一个结点
        BigIntNode* newNode = new BigIntNode();
        newNode->data = a;
        newNode->pre = rear;
        newNode->next = NULL;
        rear->next = newNode;
        rear = newNode;
    }

    void print() {
        BigIntNode* tmp = rear;
        while (tmp != head) {
            cout << tmp->data;
            tmp = tmp->pre;
        }
        cout << endl;
    }

    int add(BigIntNode* tmp, int val) {
        if (tmp == NULL) {
            create(val);
        } else {
            tmp->data += val;
            if (tmp->data >= 10) {
                int j = tmp->data / 10;
                tmp->data = tmp->data % 10;
                return j;
            }
        }
        return 0;
    }

    void multiply(BigInt& b) {
        BigInt result;
        int full = 0;
        BigIntNode* cur = result.head; // 错位相加
        for (BigIntNode* r2 = b.rear; r2 != b.head; r2 = r2->pre) {
            BigIntNode* tmp = cur; // 具体实现每位加法
            for (BigIntNode* r1 = rear; r1 != head; r1 = r1->pre) {
                full += r2->data * r1->data;
                full = result.add(tmp->next, full % 10) + full / 10; // 考虑两种情况
                tmp = tmp->next;
            }
            cur = cur->next;
            if (full != 0) result.create(full);
            full = 0;
        }
        result.print();
    }
};

int main() {
    string a = "123456789123456789";
    BigInt tmp1;
    tmp1.create(a);
    string b = "987654321987654321";
    BigInt tmp2;
    tmp2.create(b);

    tmp1.multiply(tmp2);

    return 0;
}

Java代码实现

class BigIntNode {
    int data;
    BigIntNode pre;
    BigIntNode next;
}

class BigInt {
    BigIntNode head;
    BigIntNode rear;

    BigInt() {
        head = new BigIntNode(); // 虚的
        rear = head; // 指向最后一个
    }

    void create(String a) { // 尾插
        char[] b = a.toCharArray();
        for (int i = 0; i < a.length(); i++) {
            BigIntNode newNode = new BigIntNode();
            newNode.data = b[i] - '0';
            newNode.pre = rear;
            newNode.next = null;
            rear.next = newNode;
            rear = newNode;
        }
    }

    void create(int a) { // 插入一个结点
        BigIntNode newNode = new BigIntNode();
        newNode.data = a;
        newNode.pre = rear;
        newNode.next = null;
        rear.next = newNode;
        rear = newNode;
    }

    void print() {
        BigIntNode tmp = rear;
        while (tmp != head) {
            System.out.print(tmp.data);
            tmp = tmp.pre;
        }
        System.out.println();
    }

    int add(BigIntNode tmp, int val) {
        if (tmp == null) {
            create(val);
        } else {
            tmp.data += val;
            if (tmp.data >= 10) {
                int j = tmp.data / 10;
                tmp.data = tmp.data % 10;
                return j;
            }
        }
        return 0;
    }

    void multiply(BigInt b) {
        BigInt result = new BigInt();
        int full = 0;
        BigIntNode cur = result.head; // 错位相加
        for (BigIntNode r2 = b.rear; r2 != b.head; r2 = r2.pre) {
            BigIntNode tmp = cur; // 具体实现每位加法
            for (BigIntNode r1 = rear; r1 != head; r1 = r1.pre) {
                full += r2.data * r1.data;
                full = result.add(tmp.next, full % 10) + full / 10; // 考虑两种情况
                tmp = tmp.next;
            }
            cur = cur.next;
            if (full != 0) result.create(full);
            full = 0;
        }
        result.print();
    }
}

public class Main {
    public static void main(String[] args) {
        String a = "123456789123456789";
        BigInt tmp1 = new BigInt();
        tmp1.create(a);
        String b = "987654321987654321";
        BigInt tmp2 = new BigInt();
        tmp2.create(b);

        tmp1.multiply(tmp2);
    }
}

Python代码实现

class BigIntNode:
    def __init__(self):
        self.data = 0
        self.pre = None
        self.next = None

class BigInt:
    def __init__(self):
        self.head = BigIntNode() # 虚的
        self.rear = self.head # 指向最后一个

    def create(self, a): # 尾插
        b = str(a)
        for digit in b:
            new_node = BigIntNode()
            new_node.data = int(digit)
            new_node.pre = self.rear
            new_node.next = None
            self.rear.next = new_node
            self.rear = new_node

    def add(self, tmp, val):
        if tmp is None:
            self.create(val)
        else:
            tmp.data += val
            if tmp.data >= 10:
                j = tmp.data // 10
                tmp.data %= 10
                return j
        return 0

    def print(self):
        tmp = self.rear
        while tmp != self.head:
            print(tmp.data, end="")
            tmp = tmp.pre
        print()

    def multiply(self, b):
        result = BigInt()
        full = 0
        cur = result.head # 错位相加
        r2 = b.rear
        while r2 != b.head:
            tmp = cur # 具体实现每位加法
            r1 = self.rear
            while r1 != self.head:
                full += r2.data * r1.data
                full = result.add(tmp.next, full % 10) + full // 10 # 考虑两种情况
                tmp = tmp.next
                r1 = r1.pre
            cur = cur.next
            if full != 0:
                result.create(full)
            full = 0
            r2 = r2.pre
        result.print()

if __name__ == "__main__":
    a = "123456789123456789"
    tmp1 = BigInt()
    tmp1.create(a)
    b = "987654321987654321"
    tmp2 = BigInt()
    tmp2.create(b)

    tmp1.multiply(tmp2)

运行结果

举例演示

假设我们要计算两个大数 123 和 456 的乘积。用代码中链表来存储和计算这些大数。

操作步骤

1. 链表表示：

   • 123 被存储为链表：1 -> 2 -> 3（从左到右表示高位到低位）。
   • 456 被存储为链表：4 -> 5 -> 6（同样是高位到低位）。

2. 逐位相乘：

   • 第一轮：3（第一个数最低位） 乘以 6，5，4（第二个数的每一位）：

     • 3 * 6 = 18，结果链表中加入 8，进位 1。
     • 3 * 5 = 15，加上进位 1，结果是 16，链表加入 6，进位 1。
     • 3 * 4 = 12，加上进位 1，结果是 13，链表加入 3，进位 1。
     • 最后一个进位 1，链表加入 1。 结果链表现在是：1 -> 3 -> 6 -> 8。这是当前乘积的部分结果。

   • 第二轮：2 乘以 6，5，4：

     • 2 * 6 = 12，我们将 12 加到链表当前值 6 上，结果是 18，将 8 加入链表，进位为 1。
     • 2 * 5 = 10，加上进位 1，结果是 11，将 1 加入链表，进位为 1。再加上 3，结果为 4。
     • 2 * 4 = 8，加上进位 1，结果是 9，将 9 加入链表。再加上 1，结果为 10。

     结果链表更新为：1 -> 0 -> 4 -> 8 -> 8。当前乘积的部分结果。

   • 第三轮：1 乘以 6，5，4：

     • 1 * 6 = 6，我们将 6 加到链表当前值 4 上，结果是 10，将 0 加入链表，进位为 1。
     • 1 * 5 = 5，加上进位 1，结果是 6，将 6 加入链表。
     • 1 * 4 = 4，加上进位 1，结果是 5，将 5 加入链表。

     最终乘积链表：5 -> 6 -> 0 -> 8 -> 8。

3. 结果输出：

   • 最终乘积链表为 56088，这就是 123 * 456 的乘积。

图示

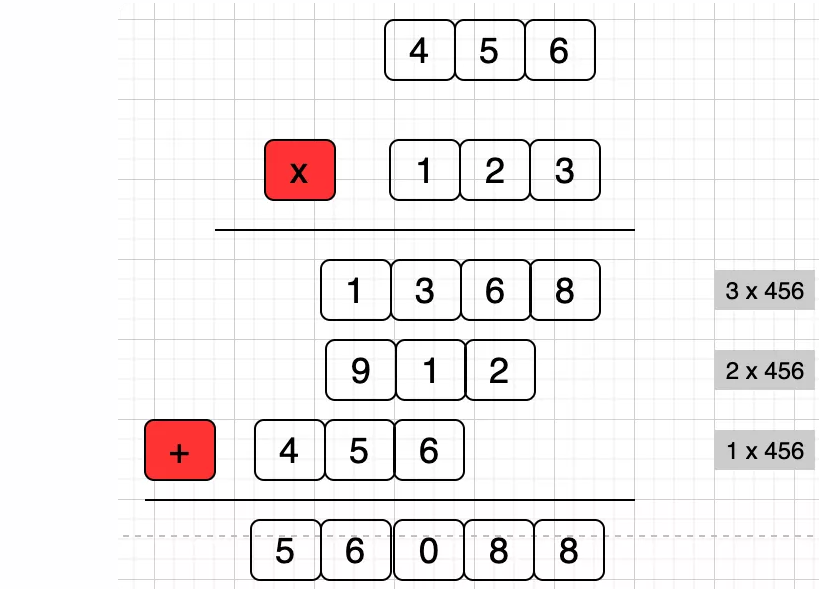
输出过程

• 输出的链表内容是 56088，这正是 123 * 456 = 56088 的正确结果。

简单总结

本节主要讲解了如何使用链表解决一些大数的计算问题。

第二节

本节旨在让学生深入理解回文链表。回文链表是面试中较为常见的题目，具体为验证给定的单链表是否为回文链表。回文链表指的是链表的值序列从前往后和从后往前完全相同。例如，链表 1 -> 2 -> 2 -> 1 是回文链表，而 1 -> 2 -> 3 不是。

知识点：

（1）回文链表检测-数组复制法（2）回文链表检测-快慢指针法

回文链表检测-数组复制法

Leetcode-回文链表

数组复制法是一种直观且易于实现的方法，算法简单，容易理解，适合不太熟悉链表操作的初学者。

算法思路

数组复制法的基本思路是将链表中的元素存储到一个数组中，然后使用双指针技术判断数组是否为回文。具体步骤如下：

1. 复制链表到数组：遍历链表，将所有节点的值存入数组中。
2. 双指针法判断回文：通过使用双指针，分别指向数组的头部和尾部，逐步比较两者的值。如果存在不同，则链表不是回文。如果全部值相同，则链表是回文。

链表：
1 -> 2 -> 3 -> 2 -> 1 -> nullptr

初始化为 vals = [1, 2, 3, 2, 1]

双指针比较数组元素：

• 初始化 i = 0 和 j = 4（vals.size() - 1）。
• 比较 vals[0] 和 vals[4]，即 1 和 1，相等，继续向内移动指针。
• 比较 vals[1] 和 vals[3]，即 2 和 2，相等，继续向内移动指针。
• 比较 vals[2] 和 vals[2]，即 3 和 3，相等，指针相遇。

代码实现

C++代码实现

class Solution {
public:
    bool isPalindrome(ListNode* head) {
        vector<int> vals;
        while (head != nullptr) {
            vals.emplace_back(head->val);
            head = head->next;
        }
        for (int i = 0, j = (int)vals.size() - 1; i < j; ++i, --j) {
            if (vals[i] != vals[j]) {
                return false;
            }
        }
        return true;
    }
};

Java代码实现

class Solution {
    public boolean isPalindrome(ListNode head) {
        List<Integer> vals = new ArrayList<Integer>();

        // 将链表的值复制到数组中
        ListNode currentNode = head;
        while (currentNode != null) {
            vals.add(currentNode.val);
            currentNode = currentNode.next;
        }

        // 使用双指针判断是否回文
        int front = 0;
        int back = vals.size() - 1;
        while (front < back) {
            if (!vals.get(front).equals(vals.get(back))) {
                return false;
            }
            front++;
            back--;
        }
        return true;
    }
}

Python代码实现

class Solution:
    def isPalindrome(self, head: ListNode) -> bool:
        vals = []
        current_node = head
        while current_node is not None:
            vals.append(current_node.val)
            current_node = current_node.next
        return vals == vals[::-1]

回文链表检测-快慢指针法

Leetcode-回文链表

算法思路

判定回文链表的快慢指针法（也称为"快慢指针技巧"或"龟兔赛跑法"）的基本思路是通过快慢指针找到链表的中点，然后反转链表的后半部分，最后通过比较前半部分和反转后的后半部分来判断链表是否为回文。这样可以避免额外的空间开销。

1. 使用快慢指针找到链表的中点：

   • 快指针每次走两步，慢指针每次走一步。快指针走到链表末尾时，慢指针恰好到达链表的中间位置。

2. 反转链表的后半部分：

   • 在慢指针找到中点后，反转链表的后半部分。这样，后半部分的节点顺序会与前半部分相反。这里以长度奇偶性分别调整。

   

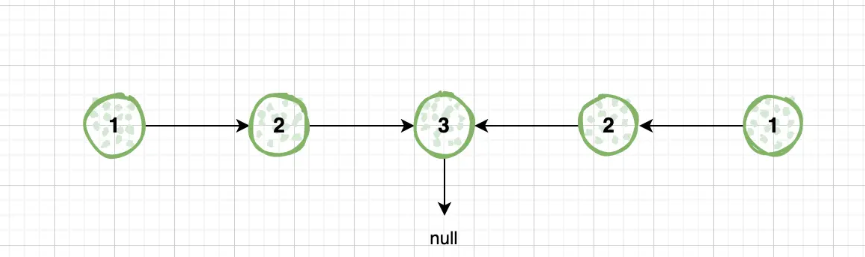
1. 比较前半部分与反转后的后半部分：

   • 通过再用一个指针遍历链表的前半部分，同时用另一个指针遍历反转后的后半部分。如果两者的值相同，链表是回文；如果有任何不相同的值，链表不是回文。

2. 恢复链表（可选）：

   • 如果不需要修改链表，可以选择在判断完成后将后半部分恢复为原来的顺序，确保链表结构不变。

步骤

初始链表

1 -> 2 -> 3 -> 2 -> 1

Step 1: 找到前半部分链表的尾节点

通过快慢指针找到链表的中点，slow 最终指向 3，返回该节点作为前半部分链表的尾节点。

1 -> 2 -> 3 | 2 -> 1

Step 2: 反转后半部分链表

反转从 slow->next 开始的链表（即 2 -> 1），得到 1 -> 2：

1 -> 2 -> 3 | 1 -> 2

Step 3: 比较前半部分和反转后的后半部分

• 比较 1 和 1：相等，继续。
• 比较 2 和 2：相等，继续。
• 比较 3 和 3：相等，继续。

链表为回文。

Step 4: 恢复链表结构

反转后半部分链表，将 1 -> 2 恢复为 2 -> 1，得到原链表结构。

1 -> 2 -> 3 -> 2 -> 1

代码实现

C++代码实现

class Solution {
public:
    bool isPalindrome(ListNode* head) {
        // 如果链表为空或只有一个节点，直接返回 true，因为空链表或单节点链表是回文
        if (head == nullptr) {
            return true;
        }

        // Step 1: 找到前半部分链表的尾节点，并反转后半部分链表
        ListNode* firstHalfEnd = endOfFirstHalf(head);  // 获取前半部分链表的尾节点
        ListNode* secondHalfStart = reverseList(firstHalfEnd->next);  // 反转后半部分链表

        // Step 2: 判断前半部分和后半部分是否回文
        ListNode* p1 = head;  // p1 指向链表的头节点（前半部分）
        ListNode* p2 = secondHalfStart;  // p2 指向反转后的后半部分
        bool result = true;  // 默认回文，若发现不匹配则更新为 false
        while (result && p2 != nullptr) {  // 比较前半部分和后半部分
            if (p1->val != p2->val) {  // 如果两个部分的值不相等，说明不是回文
                result = false;
            }
            p1 = p1->next;  // p1 向前半部分的下一个节点移动
            p2 = p2->next;  // p2 向后半部分的下一个节点移动
        }

        // Step 3: 还原链表结构
        firstHalfEnd->next = reverseList(secondHalfStart);  // 将后半部分反转回原链表结构
        return result;  // 返回是否回文的结果
    }

    // 该方法反转链表
    ListNode* reverseList(ListNode* head) {
        ListNode* prev = nullptr;  // 反转时的前驱节点
        ListNode* curr = head;  // 当前节点
        while (curr != nullptr) {  // 遍历链表并反转节点指向
            ListNode* nextTemp = curr->next;  // 保存当前节点的下一个节点
            curr->next = prev;  // 反转当前节点的指向
            prev = curr;  // 更新前驱节点为当前节点
            curr = nextTemp;  // 当前节点移动到下一个节点
        }
        return prev;  // 返回反转后的链表头节点
    }

    // 该方法通过快慢指针找到链表的中点，返回前半部分的尾节点
    ListNode* endOfFirstHalf(ListNode* head) {
        ListNode* fast = head;  // 快指针，每次移动两步
        ListNode* slow = head;  // 慢指针，每次移动一步
        while (fast->next != nullptr && fast->next->next != nullptr) {  // 快指针每次移动两步，慢指针移动一步
            fast = fast->next->next;  // 快指针
            slow = slow->next;  // 慢指针
        }
        return slow;  // 慢指针到达链表中点，返回前半部分链表的尾节点
    }
};

Java代码实现

class Solution {
    public boolean isPalindrome(ListNode head) {
        // 如果链表为空，直接返回 true，因为空链表视为回文链表
        if (head == null) {
            return true;
        }

        // Step 1: 找到前半部分链表的尾节点，并反转后半部分链表
        ListNode firstHalfEnd = endOfFirstHalf(head); // 获取前半部分链表的尾节点
        ListNode secondHalfStart = reverseList(firstHalfEnd.next); // 反转后半部分链表

        // Step 2: 比较前后两部分链表的值
        ListNode p1 = head; // p1 指向链表的头部
        ListNode p2 = secondHalfStart; // p2 指向反转后的后半部分链表
        boolean result = true;
        while (result && p2 != null) { // 只要 p2 还有节点未比较
            if (p1.val != p2.val) { // 如果值不同，说明链表不是回文
                result = false;
            }
            p1 = p1.next; // 向前半部分链表的下一个节点移动
            p2 = p2.next; // 向后半部分链表的下一个节点移动
        }        

        // Step 3: 还原链表结构
        firstHalfEnd.next = reverseList(secondHalfStart); // 反转后的后半部分再反转回来，恢复原链表

        return result; // 返回是否回文的结果
    }

    // 该方法反转链表
    private ListNode reverseList(ListNode head) {
        ListNode prev = null; // 反转链表时的前驱节点
        ListNode curr = head; // 当前节点
        while (curr != null) {
            ListNode nextTemp = curr.next; // 保存当前节点的下一个节点
            curr.next = prev; // 反转当前节点的指向
            prev = curr; // 前驱节点移动到当前节点
            curr = nextTemp; // 当前节点移动到下一个节点
        }
        return prev; // 返回反转后的链表头节点
    }

    // 该方法使用快慢指针找到链表的中点，返回前半部分的尾节点
    private ListNode endOfFirstHalf(ListNode head) {
        ListNode fast = head; // 快指针每次移动两步
        ListNode slow = head; // 慢指针每次移动一步
        // 快指针到达链表末尾时，慢指针恰好到达链表的中点
        while (fast.next != null && fast.next.next != null) {
            fast = fast.next.next; // 快指针每次走两步
            slow = slow.next; // 慢指针每次走一步
        }
        return slow; // 返回前半部分链表的尾节点
    }
}

Python代码实现

class Solution:

    def isPalindrome(self, head: ListNode) -> bool:
        # 如果链表为空，直接返回 True，因为空链表视为回文链表
        if head is None:
            return True

        # 找到前半部分链表的尾节点并反转后半部分链表
        # 1. 使用 `end_of_first_half` 找到链表的中点（前半部分的尾节点）
        # 2. 通过 `reverse_list` 反转链表的后半部分
        first_half_end = self.end_of_first_half(head)
        second_half_start = self.reverse_list(first_half_end.next)

        # 判断链表是否为回文
        result = True
        first_position = head
        second_position = second_half_start
        
        # 使用两个指针分别遍历前半部分和反转后的后半部分进行比较
        while result and second_position is not None:
            if first_position.val != second_position.val:  # 如果两个节点值不同，则不是回文
                result = False
            first_position = first_position.next  # 向前半部分的下一个节点移动
            second_position = second_position.next  # 向后半部分的下一个节点移动

        # 还原链表（恢复原链表结构），反转回后半部分
        first_half_end.next = self.reverse_list(second_half_start)
        return result  # 返回回文判定结果

    # 该函数通过快慢指针找到链表的中点（前半部分的尾节点）
    def end_of_first_half(self, head):
        fast = head  # 快指针每次移动两步
        slow = head  # 慢指针每次移动一步
        while fast.next is not None and fast.next.next is not None:
            fast = fast.next.next  # 快指针前进两步
            slow = slow.next  # 慢指针前进一步
        return slow  # 慢指针到达链表的中点，返回慢指针

    # 该函数用于反转链表
    def reverse_list(self, head):
        previous = None  # 初始时反转链表为空
        current = head   # 当前指向原链表的头节点
        while current is not None:
            next_node = current.next  # 保存下一个节点
            current.next = previous  # 反转当前节点的指针
            previous = current  # 将当前节点设为前一个节点
            current = next_node  # 当前节点后移
        return previous  # 返回反转后的链表头节点

简单总结

在本节中，我们学习了判定回文链表。学习回文链表不仅是提升链表操作能力的好方法，而且能够帮助我们培养多种解题技巧，提升面试中的表现，进而更好地准备数据结构与算法相关的面试题。

第三节

本节旨在让学生深入理解环形链表。面试中常用的算法来检测环形链表，即使用快指针和慢指针，快指针每次走两步，慢指针每次走一步。如果两者相遇，则存在环。一些进阶问题会要求找到环的入口节点，这需要候选人深入理解快慢指针的特性，并通过数学推导确定入口位置。通过实验，学生将学习以下内容 ：

知识点：

（1）环形链表（2）环形链表检测

环形链表

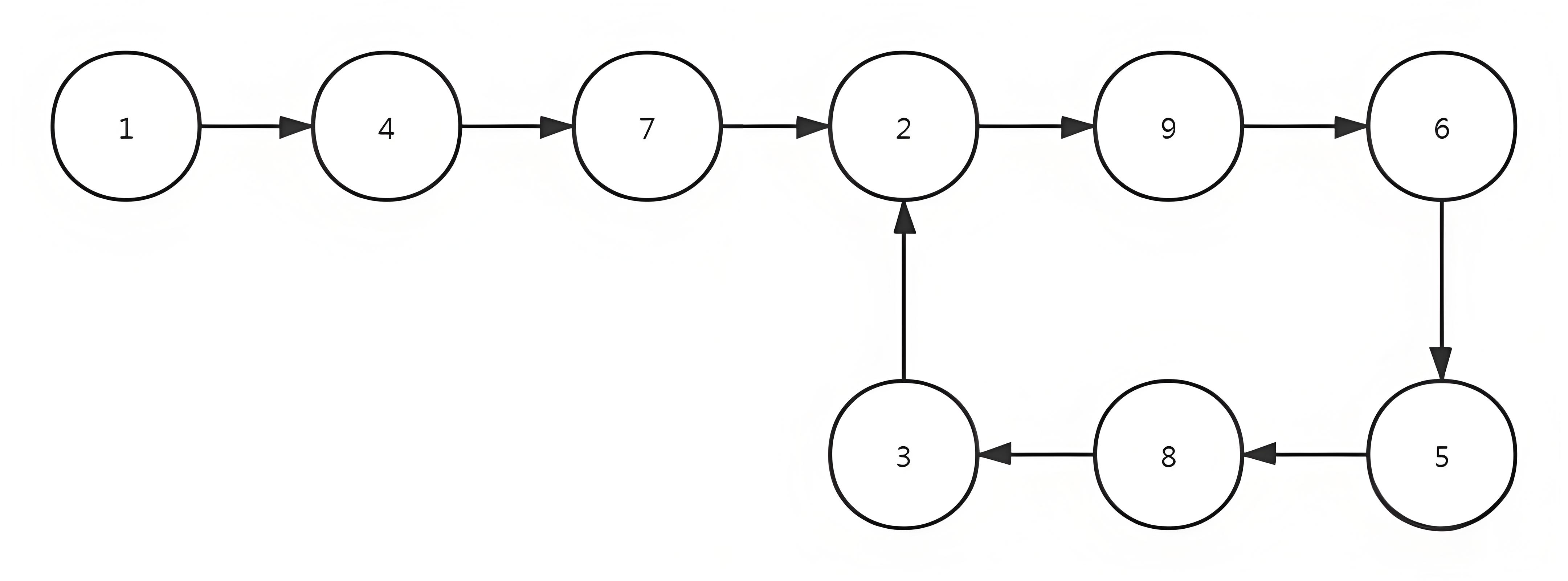
环形链表定义

环形链表是一种特殊的链表结构，其中链表的最后一个节点指向链表中的某个先前节点，形成一个环状结构。换句话说，链表中的最后一个节点指向链表中的某个非尾节点，而不是指向空值。

图示

应用场景

这种环形结构可以用于各种应用场景，例如：

• 循环队列：环形链表可以用于实现循环队列，其中队列的尾部连接到队列的头部，形成一个循环。

• 轮询操作：在分布式系统中，环形链表可以用于轮询节点，每个节点代表一个处理单元或任务，通过环形链表可以实现轮询操作，确保每个节点都有机会被处理。

• 约瑟夫问题：环形链表可以用于解决约瑟夫问题，即n个人围成一圈，从第一个人开始报数，报到m的人出列，然后从出列的人的下一个人开始重新报数，直到所有人出列为止。

• 快慢指针技巧：在算法问题中，环形链表常常与快慢指针技巧结合使用，用于检测链表中是否存在环以及找到环的起点等问题。

总的来说，环形链表是一种特殊的链表结构，具有特定的环形连接方式，可用于实现各种算法和数据结构，以及解决各种实际问题。

环形链表检测

Leetcode-判定环形链表

Set保存法

对于判断链表是否为环形链表，我们可以利用集合来记录已经访问过的节点。

具体步骤

• 从头节点开始遍历链表。
• 每次遍历到一个节点时，检查该节点是否已经在集合中。
• 如果节点不在集合中，则将该节点加入集合中，并继续遍历下一个节点。
• 如果节点已经在集合中，则说明链表存在环，返回 True。
• 如果遍历到链表末尾（即节点的 next 指针为 null ），则说明链表不是环形链表，返回 False。

这种方法利用了集合的快速查找特性，可以在 O(n) 的时间复杂度内完成判断。

图示

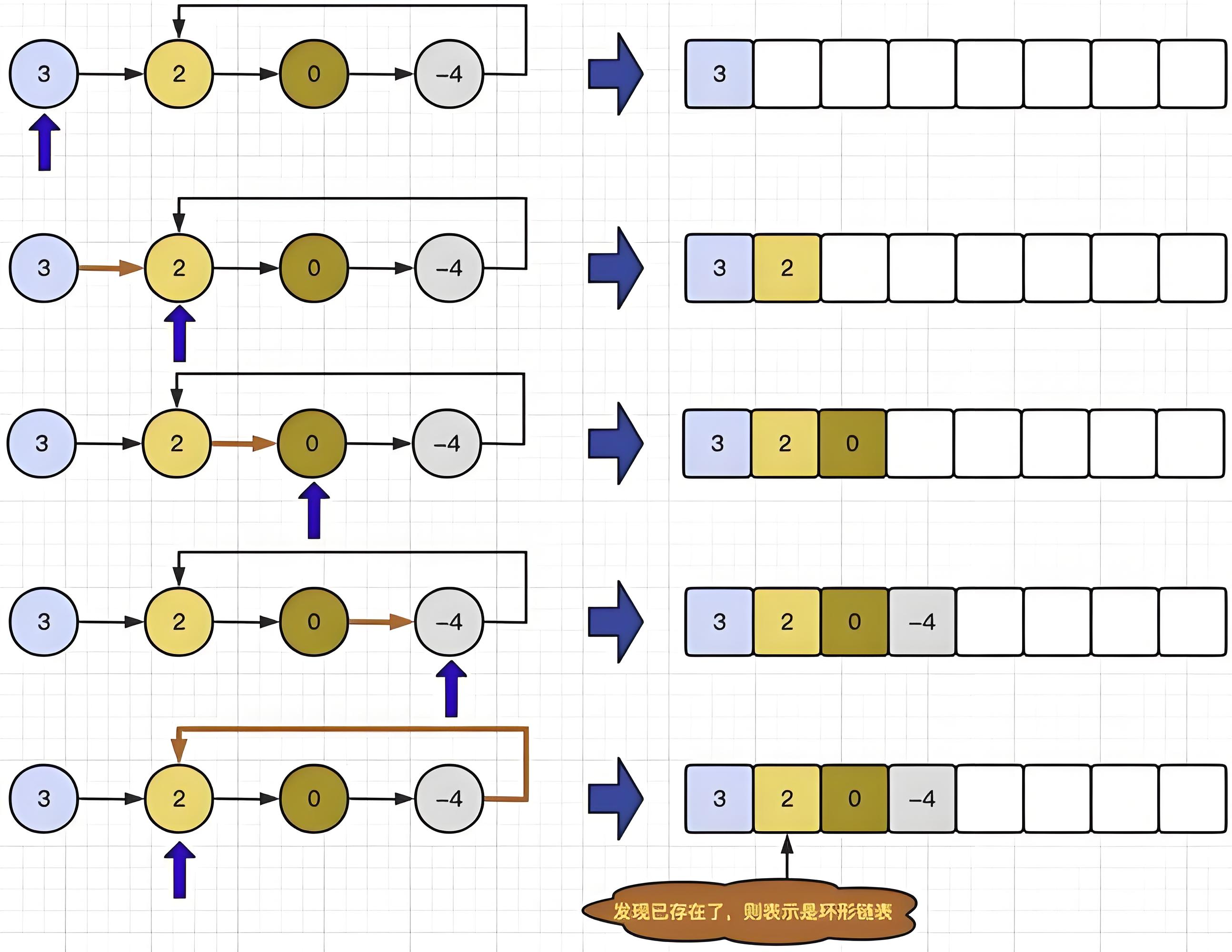
代码实现

C++代码实现

#include <unordered_set>

struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(nullptr) {}
};

class Solution {
public:
    bool hasCycle(ListNode *head) {
        std::unordered_set<ListNode*> visited; // 用于存储已访问过的节点地址的哈希集合
        while (head != nullptr) { // 遍历链表直到链表末尾
            if (visited.find(head) != visited.end()) // 如果当前节点已经在集合中出现过，说明存在环
                return true;
            visited.insert(head); // 将当前节点加入到集合中
            head = head->next; // 移动到下一个节点
        }
        return false; // 遍历完整个链表都没发现环，返回false
    }
};

Java代码实现

import java.util.HashSet;
import java.util.Set;

class ListNode {
    int val;
    ListNode next;
    ListNode(int x) {
        val = x;
        next = null;
    }
}

public class Solution {
    public boolean hasCycle(ListNode head) {
        Set<ListNode> visited = new HashSet<>(); // 用于存储已访问过的节点的集合
        while (head != null) { // 遍历链表直到链表末尾
            if (visited.contains(head)) // 如果当前节点已经在集合中出现过，说明存在环
                return true;
            visited.add(head); // 将当前节点加入到集合中
            head = head.next; // 移动到下一个节点
        }
        return false; // 遍历完整个链表都没发现环，返回false
    }
}

Python代码实现

class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None

class Solution:
    def hasCycle(self, head):
        visited = set()  # 用于存储已访问过的节点的集合
        while head is not None:  # 遍历链表直到链表末尾
            if head in visited:  # 如果当前节点已经在集合中出现过，说明存在环
                return True
            visited.add(head)  # 将当前节点加入到集合中
            head = head.next  # 移动到下一个节点
        return False  # 遍历完整个链表都没发现环，返回False

快慢指针技巧

检测环形链表通常使用快慢指针技巧。

具体步骤

• 初始化快慢指针：定义两个指针，一个快指针（通常每次移动两步），一个慢指针（每次移动一步）。初始时，将这两个指针都指向链表的头部。

• 移动指针：在每一步中，快指针向前移动两步，慢指针向前移动一步。如果链表中存在环，快指针最终会追上慢指针，因为快指针每次多走一步，所以它会在某一时刻绕着环追上慢指针。

• 检测环：在移动过程中，如果快指针和慢指针相遇了（即它们指向了同一个节点），则说明链表中存在环。如果快指针在某一步到达了链表的末尾（即指向了空节点），则说明链表中不存在环。

• 找到环的起点（可选）：如果快指针和慢指针相遇了，表明链表中存在环。此时，将其中一个指针移到链表的头部，并以相同的速度移动两个指针，直到它们再次相遇。相遇的节点即为环的起点。

通过这些步骤，我们可以确定链表中是否存在环，并在需要时找到环的起点。

图示

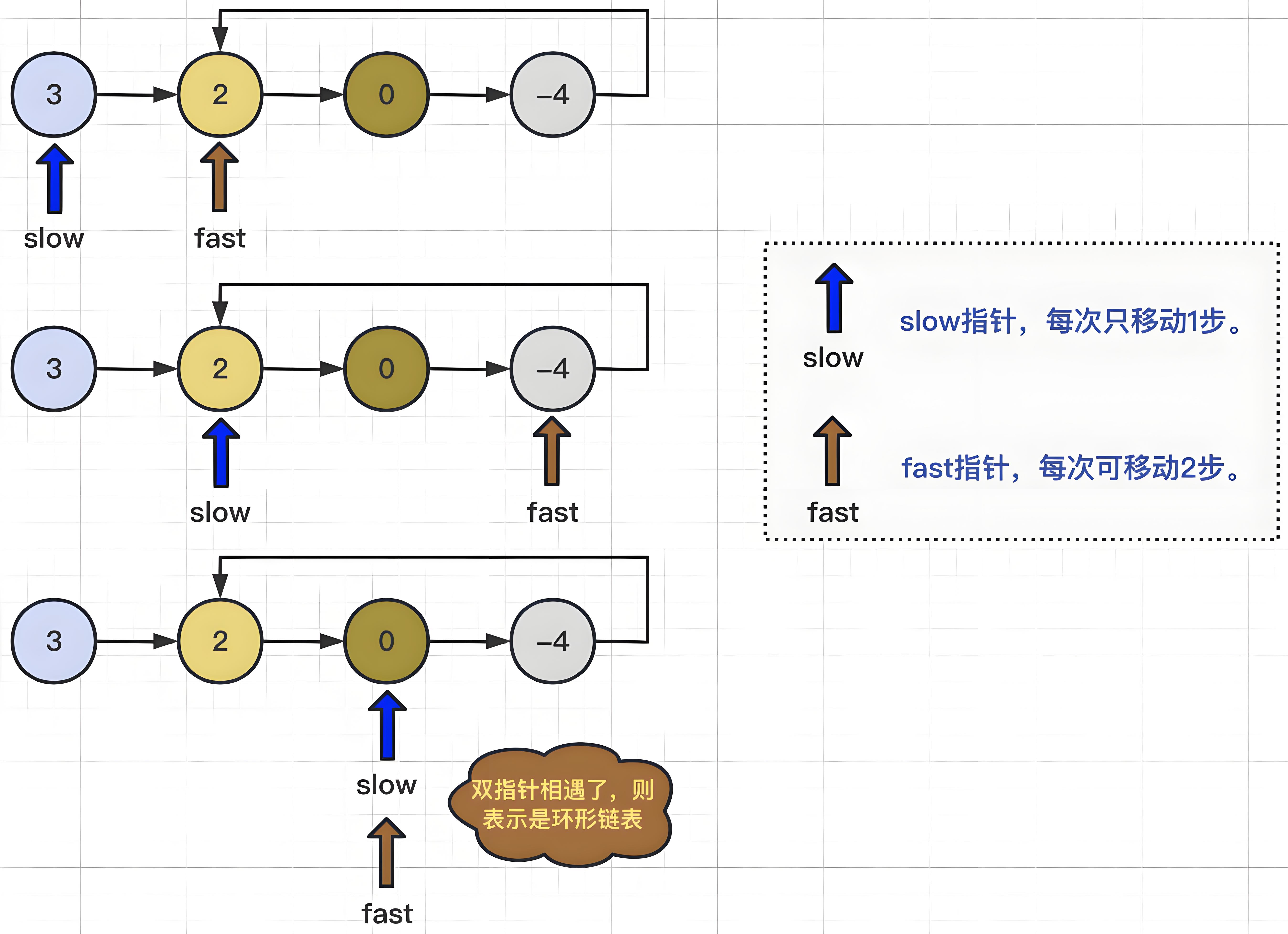
下列代码使用了快慢指针方法来检测链表中是否存在环。首先，定义了两个指针，slow 和 fast，初始时 slow 指向头节点，fast 指向头节点的下一个节点（如果头节点不为空的话）。然后在循环中，每次慢指针 slow 移动一步，快指针 fast 移动两步，直到快指针到达链表末尾（即 fast 为nullptr ）或者快指针追上慢指针（即 slow == fast ），如果是后者，则说明链表中存在环，返回 true；否则，返回 false。

代码实现

C++代码实现

struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(nullptr) {}
};

class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode *slow = head, *fast = (head == nullptr) ? nullptr : head->next;
        while (fast != nullptr) {
            if (slow == fast) return true;  // 如果慢指针和快指针相遇，则说明存在环
            slow = slow->next;  // 慢指针移动一步
            fast = (fast->next == nullptr) ? nullptr : fast->next->next;  // 快指针移动两步
        }
        return false;  // 如果快指针到达链表末尾，则不存在环
    }
};

Java代码实现

class ListNode {
    int val;  // 节点的值
    ListNode next;  // 下一个节点的指针
    ListNode(int x) {
        val = x;  // 初始化节点值
        next = null;  // 初始化下一个节点指针为空
    }
}

public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode slow = head, fast = (head == null) ? null : head.next;  // 初始化慢指针和快指针，慢指针从头节点开始，快指针从头节点的下一个节点开始（如果头节点不为空的话）
        while (fast != null) {  // 当快指针不为空时循环
            if (slow == fast) return true;  // 如果慢指针和快指针相遇，则说明存在环，返回true
            slow = slow.next;  // 慢指针移动一步
            fast = (fast.next == null) ? null : fast.next.next;  // 快指针移动两步
        }
        return false;  // 如果快指针到达链表末尾，则不存在环，返回false
    }
}

Python代码实现

class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None

class Solution:
    def hasCycle(self, head: ListNode) -> bool:
        slow = head
        fast = head.next if head else None
        while fast:
            if slow == fast:
                return True
            slow = slow.next
            fast = fast.next.next if fast.next else None
        return False

简单总结

在本节中，我们学习了环形链表检测。通过这个学习，我了解到了如何使用快慢指针来检测链表中是否存在环，以及其原理。这种方法不仅简单高效，而且在空间复杂度上只需要 O(1) 的额外空间，非常适合实际应用中处理大规模数据。

第四节

本节主要介绍如何删除链表节点。删除节点需要对链表的指针操作非常熟悉，尤其是理解如何在链表中调整节点指针以删除目标节点而不破坏链表的结构。在执行删除操作时，需要正确地遍历链表以找到需要删除的节点，确保链表的完整性。

知识点：

（1）删除链表节点

删除链表节点

Leetcode-删除链表节点

题目描述

给定单向链表的头指针和一个要删除的节点的值，定义一个函数删除该节点。

返回删除后的链表的头节点。

解法

定位节点： 遍历链表，直到 head.val == val 时跳出，即可定位目标节点。 修改引用： 设节点 cur 的前驱节点为 pre ，后继节点为 cur.next ；则执行 pre.next = cur.next ，即可实现删除 cur 节点。

具体可以这样做：

• 特例处理： 当应删除头节点 head 时，直接返回 head.next 即可
• 初始化： pre = head , cur = head.next 。
• 定位节点： 当 cur 为空或 cur 节点值等于 val 时跳出。
• 保存当前节点索引，即 pre = cur 。
• 遍历下一节点，即 cur = cur.next 。
• 删除节点： 若 cur 指向某节点，则执行 pre.next = cur.next ；若 cur 指向 null ，代表链表中不包含值为 val 的节点。
• 返回值： 返回链表头部节点 head 即可。

图示

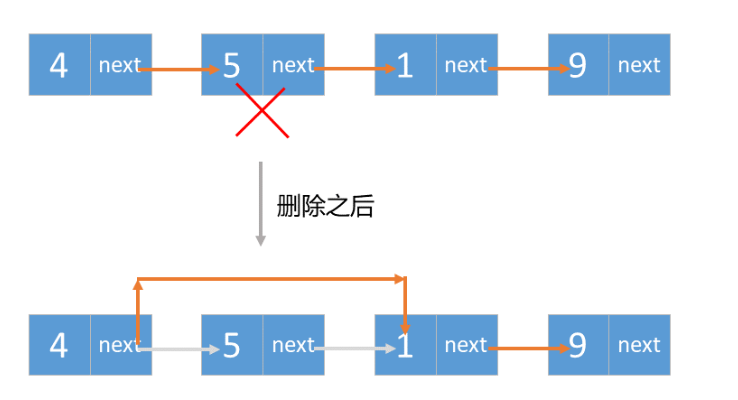
代码实现

C++代码实现

class Solution {
public:
    ListNode* deleteNode(ListNode* head, int val) {
        if(head->val == val) return head->next;
        ListNode *pre = head, *cur = head->next;
        while(cur != nullptr && cur->val != val) {
            pre = cur;
            cur = cur->next;
        }
        if(cur != nullptr) pre->next = cur->next;
        return head;
    }
};

Java代码实现

class Solution {
    public ListNode deleteNode(ListNode head, int val) {
        if(head.val == val) return head.next;
        ListNode pre = head, cur = head.next;
        while(cur != null && cur.val != val) {
            pre = cur;
            cur = cur.next;
        }
        if(cur != null) pre.next = cur.next;
        return head;
    }
}

Python代码实现

class Solution:
    def deleteNode(self, head: ListNode, val: int) -> ListNode:
        if head.val == val: return head.next
        pre, cur = head, head.next
        while cur and cur.val != val:
            pre, cur = cur, cur.next
        if cur: pre.next = cur.next
        return head

简单总结

本节主要学习了如何删除链表的一个节点。某些删除节点的问题会涉及到算法思维的展示，尤其是如何在特定情况下高效删除节点，通过解决删除链表节点问题，面试官可以评估候选人处理链表操作的基础能力，以及对数据结构的理解。