量子力学中的向量可以用狄拉克符号来表示,且向量通常是复数构成的。如通常表示一个1*n的复数行向量,例如
,该向量通常也称为右矢;而
则表示
的复共轭,即
,该向量通常称为左矢。值得注意的是量子力学中为了方便进行点积运算,在对右矢取共轭时通常会对其进行转置。
用狄拉克符号表示点积运算形式如下:,因为一个向量点积自己的共轭向量得到的是一个常数,所以上式的结果是一个常数。如果
,代表向量
与向量
正交。
显然狄拉克符号要经常的涉及到取共轭的运算,下面用狄拉克符号表示出一些矢量和它们的共轭:
特别的,对于,可以给出证明:向量a、b本质上是两个特殊的矩阵(量子力学的术语中矩阵特指方阵,但向量的本质就是矩阵),a、b可以表述为A、B;
等价于
,而我们知道
,所以
,所以
与
互为复共轭。
有了量子力学中的复共轭的计算方法,我们可以构造复数向量空间。在之前线性代数的文章中我们讨论过,对于向量空间来说,最主要的是满足空间内的向量对加法和数乘封闭,而之前讨论的是实向量空间,量子力学中要讨论的是复数向量空间,其同样要满足空间内的复数向量的加法和数乘封闭。
如对于一个某空间内的向量,对于空间内的向量、
,
空间内的复数;
对于,
,如果
、
仍然在该空间内,则该空间构成一个负数向量空间。如果我们有了一个复数向量空间,那么显然这些复数向量的共轭向量可以构成一个对应的共轭向量空间。
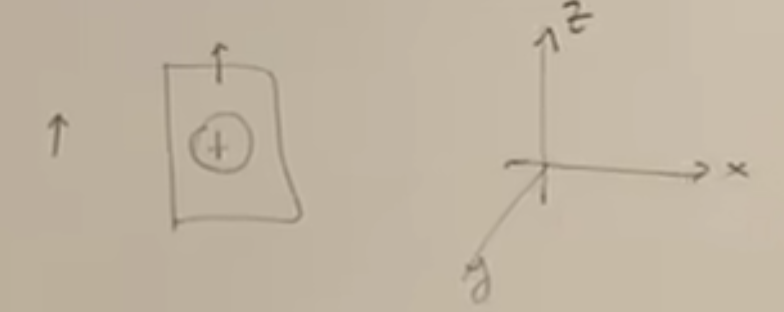
对于前一篇文章里的实验,我们现在可以用狄拉克符号来对其进行描述,对于量子比特的状态(从现在开始我们把量子比特系统称之为"自旋"),可以用一个右矢来描述。
对于二维情况下的自旋,可以有以下四种状态:
(平面坐标系里更细关于于y表示竖直向上方向,但这里我们用z来表示),表示自旋向上,狄拉克符号表示为
,自旋向下,狄拉克符号表示为
,狄拉克符号表示为
,狄拉克符号表示为
显然对于一个二维空间下的系统,使用前两个右矢就足以表达出自旋的所有状态。
接下来补充一下涉及到前篇文章中提到的实验的逻辑知识
在经典物理中,对于观测实验的实验顺序并不像在量子力学中有严格要求,因为经典物理中的观测并不会对被观测对象造成影响。但在量子力学中,观测行为本身就会影响被观测系统的状态,从而对实验结果产生影响。
假设命题A为:
命题B为:
我们给出一个命题,(或者
)在经典物理中,我们可以以任意顺序区分别检测A、B的真伪,但是在量子力学中情况不同。
假如我们先检验命题A,对自旋在z的正方向上观测,我们假设此时观测到+1,那么此时显然A为真,则AorB为真。
但如果我们先检验命题B,对自旋在x的正方向上观测,此时我们会观测到,并且各自出现的概率为0.5;如果我们观测到了
,此时再从z的正方向上观测,我们的观测结果会变成
,同样的各自出现的概率为0.5,那么此时AorB为真的概率就是0.5*0.5=0.25。
我们惊人的发现,如果先检验命题A,那么命题AorB为真的概率为1;如果先检验命题B,命题AorB的概率变成了0.25。
这是因为当我们先检验命题B时,对自旋进行的观测对系统产生了影响,使得其在z正方向的概率从100%出现+1,变成了各出现25%的+1、-1,也即观测对系统在z正方向上的状态进行了扩展。所以在量子力学中,观测实验的顺序至关重要,经过观测后的系统不可以简单的视为和观测前的系统等价。