Python拒绝采样算法优化与微调模拟

拒绝采样是一种从复杂分布中生成样本的蒙特卡洛方法，是目前LLM微调优化的关键技术。

这里尝试基于python模拟和对比多种拒绝采样的实现方法。

所用样例参考和优化自网络资料。

1 什么是拒绝采样

拒绝采样(Rejection Sampling)是一种从复杂分布中生成样本的蒙特卡洛方法。

下面将展示多种拒绝采样算法。

1.1 基础拒绝采样

• 核心原理：从提议分布生成样本，以一定概率接受

• 关键参数：常数M，需要满足 target_pdf(x) ≤ M * proposal_pdf(x)

• 优化方向：选择合适的提议分布和尽可能小的M值

1.2 自适应拒绝采样优化

• 动态调整提议分布：根据已接受的样本调整提议分布的参数

• 自动优化M值：在采样过程中重新计算最优M值

• 分批更新：每接受一定数量样本后更新提议分布

1.3 分层拒绝采样优化

• 定义域分层：将目标分布的定义域分成多个子区域

• 各层独立优化：为每个子区域选择最合适的提议分布

• 平衡采样：在各层之间合理分配采样数量

1.4 混合提议分布优化

• 多个提议分布混合：使用多个提议分布的加权和

• 自适应权重调整：根据接受率动态调整各分布的权重

• 多峰分布匹配：特别适合多峰目标分布

2 python模拟拒绝采样

2.1 拒绝采样优化模拟示例

下面将展示一个完整的Python实现，包括基础版本和多个优化版本。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import time
from functools import wraps
import warnings
warnings.filterwarnings('ignore')

# ==================== 基础拒绝采样算法 ====================
def basic_rejection_sampling(target_pdf, proposal_pdf, proposal_rv, M, n_samples=1000, max_iter=10000):
    """
    基础拒绝采样算法
    
    参数:
    target_pdf: 目标分布的概率密度函数
    proposal_pdf: 提议分布的概率密度函数
    proposal_rv: 提议分布的随机变量生成函数
    M: 常数M，使得 target_pdf(x) ≤ M * proposal_pdf(x) 对所有x成立
    n_samples: 需要生成的样本数量
    max_iter: 最大迭代次数（防止无限循环）
    
    返回:
    samples: 从目标分布中采样的样本
    acceptance_rate: 接受率
    """
    samples = []
    attempts = 0
    
    while len(samples) < n_samples and attempts < max_iter:
        attempts += 1
        
        # 1. 从提议分布生成样本
        x = proposal_rv()
        
        # 2. 从均匀分布U(0,1)生成样本
        u = np.random.uniform(0, 1)
        
        # 3. 接受/拒绝决策
        if u < target_pdf(x) / (M * proposal_pdf(x)):
            samples.append(x)
    
    acceptance_rate = len(samples) / attempts if attempts > 0 else 0
    
    return np.array(samples), acceptance_rate

# ==================== 自适应拒绝采样优化版本 ====================
class AdaptiveRejectionSampler:
    """
    自适应拒绝采样器 - 优化版本1: 动态调整提议分布
    """
    def __init__(self, target_pdf, initial_proposal, domain=(-10, 10)):
        """
        初始化自适应拒绝采样器
        
        参数:
        target_pdf: 目标分布的概率密度函数
        initial_proposal: 初始提议分布 (dict with 'pdf' and 'rv' functions)
        domain: 采样域
        """
        self.target_pdf = target_pdf
        self.proposal_pdf = initial_proposal['pdf']
        self.proposal_rv = initial_proposal['rv']
        self.domain = domain
        self.samples = []
        self.rejections = []
        self.M_history = []
        
    def find_optimal_M(self, n_test=1000):
        """
        通过测试点找到最优的M值
        
        参数:
        n_test: 测试点数量
        
        返回:
        optimal_M: 最优M值
        """
        test_points = np.linspace(self.domain[0], self.domain[1], n_test)
        ratios = []
        
        for x in test_points:
            target_val = self.target_pdf(x)
            proposal_val = self.proposal_pdf(x)
            if proposal_val > 0:
                ratio = target_val / proposal_val
                ratios.append(ratio)
        
        # 使用最大比值的1.1倍作为M，确保覆盖
        optimal_M = np.max(ratios) * 1.1 if ratios else 2.0
        return optimal_M
    
    def adaptive_sampling(self, n_samples=1000, adapt_every=100, verbose=False):
        """
        自适应采样过程
        
        参数:
        n_samples: 需要生成的样本数量
        adapt_every: 每多少个样本调整一次提议分布
        verbose: 是否显示详细信息
        
        返回:
        samples: 采样结果
        acceptance_rate: 平均接受率
        """
        samples = []
        self.M_history = []
        total_attempts = 0
        
        # 初始M值
        M = self.find_optimal_M()
        self.M_history.append(M)
        
        for batch in range(0, n_samples, adapt_every):
            batch_size = min(adapt_every, n_samples - len(samples))
            batch_samples, batch_attempts = self._sample_batch(batch_size, M)
            
            samples.extend(batch_samples)
            total_attempts += batch_attempts
            
            # 更新提议分布（基于已接受的样本）
            if len(samples) > 10:
                self._update_proposal(samples)
                M = self.find_optimal_M()
                self.M_history.append(M)
                
                if verbose:
                    acceptance = len(batch_samples) / batch_attempts if batch_attempts > 0 else 0
                    print(f"Batch {batch//adapt_every}: Acceptance rate = {acceptance:.4f}, M = {M:.4f}")
        
        acceptance_rate = len(samples) / total_attempts if total_attempts > 0 else 0
        return np.array(samples), acceptance_rate
    
    def _sample_batch(self, batch_size, M):
        """采样一个批次"""
        samples = []
        attempts = 0
        
        while len(samples) < batch_size and attempts < batch_size * 100:  # 防止无限循环
            attempts += 1
            x = self.proposal_rv()
            u = np.random.uniform(0, 1)
            
            if u < self.target_pdf(x) / (M * self.proposal_pdf(x)):
                samples.append(x)
            else:
                self.rejections.append(x)
        
        return samples, attempts
    
    def _update_proposal(self, accepted_samples):
        """基于接受的样本更新提议分布参数"""
        # 这里使用简单的高斯分布作为提议分布
        # 在实际应用中可以使用更复杂的分布
        mean = np.mean(accepted_samples)
        std = np.std(accepted_samples) + 0.1  # 加一个小值防止方差为0
        
        # 更新提议分布为新的正态分布
        self.proposal_pdf = lambda x: stats.norm.pdf(x, mean, std)
        self.proposal_rv = lambda: np.random.normal(mean, std)

# ==================== 分层拒绝采样优化版本 ====================
def stratified_rejection_sampling(target_pdf, domains, proposal_funcs, n_samples=1000):
    """
    分层拒绝采样 - 优化版本2: 将定义域分层
    
    参数:
    target_pdf: 目标分布的概率密度函数
    domains: 每个层的定义域列表 [(a1, b1), (a2, b2), ...]
    proposal_funcs: 每个层的提议分布函数列表 [{'pdf': pdf1, 'rv': rv1}, ...]
    n_samples: 需要生成的样本数量
    
    返回:
    samples: 采样结果
    acceptance_rates: 各层的接受率
    """
    samples = []
    acceptance_rates = []
    n_layers = len(domains)
    
    # 分配每层的采样数量（可以根据层的权重分配）
    samples_per_layer = n_samples // n_layers
    remainder = n_samples % n_layers
    
    for i in range(n_layers):
        # 当前层的采样数量
        layer_samples = samples_per_layer + (1 if i < remainder else 0)
        
        # 为当前层定义截断的提议分布
        a, b = domains[i]
        layer_proposal_pdf = proposal_funcs[i]['pdf']
        layer_proposal_rv = proposal_funcs[i]['rv']
        
        # 在当前层中找到M值
        test_points = np.linspace(a, b, 1000)
        max_ratio = 0
        for x in test_points:
            ratio = target_pdf(x) / layer_proposal_pdf(x)
            if ratio > max_ratio:
                max_ratio = ratio
        M = max_ratio * 1.1
        
        # 在当前层进行拒绝采样
        layer_samples_list = []
        attempts = 0
        while len(layer_samples_list) < layer_samples and attempts < layer_samples * 100:
            attempts += 1
            x = layer_proposal_rv()
            # 确保x在当前层内
            if a <= x <= b:
                u = np.random.uniform(0, 1)
                if u < target_pdf(x) / (M * layer_proposal_pdf(x)):
                    layer_samples_list.append(x)
        
        samples.extend(layer_samples_list)
        acceptance_rate = len(layer_samples_list) / attempts if attempts > 0 else 0
        acceptance_rates.append(acceptance_rate)
    
    return np.array(samples), acceptance_rates

# ==================== 混合提议分布优化版本 ====================
class MixtureProposalSampler:
    """
    混合提议分布拒绝采样 - 优化版本3: 使用多个提议分布的混合
    """
    def __init__(self, target_pdf, proposal_components):
        """
        初始化混合提议分布采样器
        
        参数:
        target_pdf: 目标分布的概率密度函数
        proposal_components: 提议分布组件列表
                            [{'pdf': pdf1, 'rv': rv1, 'weight': w1}, ...]
        """
        self.target_pdf = target_pdf
        self.components = proposal_components
        self.n_components = len(proposal_components)
        self.weights = np.array([comp['weight'] for comp in proposal_components])
        self.weights = self.weights / np.sum(self.weights)  # 归一化
    
    def sample(self, n_samples=1000):
        """执行采样"""
        samples = []
        attempts = 0
        
        while len(samples) < n_samples and attempts < n_samples * 100:
            attempts += 1
            
            # 1. 选择提议分布组件
            comp_idx = np.random.choice(self.n_components, p=self.weights)
            component = self.components[comp_idx]
            
            # 2. 从选定的组件生成样本
            x = component['rv']()
            
            # 3. 计算混合提议分布的概率密度
            mixture_pdf = 0
            for i, comp in enumerate(self.components):
                mixture_pdf += self.weights[i] * comp['pdf'](x)
            
            # 4. 计算M值（对于混合分布，需要找到全局M）
            # 这里简化处理，使用当前点的比值
            if mixture_pdf > 0:
                ratio = self.target_pdf(x) / mixture_pdf
                M = 2.0  # 简化：使用固定的M，实际应用中需要计算合适的M
                
                # 5. 接受/拒绝决策
                u = np.random.uniform(0, 1)
                if u < ratio / M:
                    samples.append(x)
        
        acceptance_rate = len(samples) / attempts if attempts > 0 else 0
        return np.array(samples), acceptance_rate

# ==================== 性能比较和可视化 ====================
def compare_sampling_methods(target_pdf, true_samples=None):
    """比较不同采样方法的性能"""
    # 定义目标分布（混合高斯分布）
    print("目标分布: 混合高斯分布")
    print("=" * 60)
    
    # 基础拒绝采样参数
    # 使用高斯分布作为提议分布
    proposal_mean = 0
    proposal_std = 2
    
    proposal_pdf = lambda x: stats.norm.pdf(x, proposal_mean, proposal_std)
    proposal_rv = lambda: np.random.normal(proposal_mean, proposal_std)
    
    # 找到合适的M值
    test_points = np.linspace(-10, 10, 1000)
    max_ratio = 0
    for x in test_points:
        ratio = target_pdf(x) / proposal_pdf(x)
        if ratio > max_ratio:
            max_ratio = ratio
    M = max_ratio * 1.1
    
    print(f"基础拒绝采样 - 使用的M值: {M:.4f}")
    
    # 方法1: 基础拒绝采样
    start_time = time.time()
    basic_samples, basic_acceptance = basic_rejection_sampling(
        target_pdf, proposal_pdf, proposal_rv, M, n_samples=2000
    )
    basic_time = time.time() - start_time
    
    print(f"基础拒绝采样 - 接受率: {basic_acceptance:.4f}, 时间: {basic_time:.4f}s")
    
    # 方法2: 自适应拒绝采样
    initial_proposal = {
        'pdf': proposal_pdf,
        'rv': proposal_rv
    }
    adaptive_sampler = AdaptiveRejectionSampler(target_pdf, initial_proposal, domain=(-10, 10))
    
    start_time = time.time()
    adaptive_samples, adaptive_acceptance = adaptive_sampler.adaptive_sampling(
        n_samples=2000, adapt_every=200, verbose=False
    )
    adaptive_time = time.time() - start_time
    
    print(f"自适应拒绝采样 - 接受率: {adaptive_acceptance:.4f}, 时间: {adaptive_time:.4f}s")
    
    # 方法3: 分层拒绝采样
    # 定义三个层和对应的提议分布
    domains = [(-10, -2), (-2, 2), (2, 10)]
    proposal_funcs = []
    for a, b in domains:
        mean = (a + b) / 2
        std = (b - a) / 4
        proposal_funcs.append({
            'pdf': lambda x, mean=mean, std=std: stats.norm.pdf(x, mean, std),
            'rv': lambda mean=mean, std=std: np.random.normal(mean, std)
        })
    
    start_time = time.time()
    stratified_samples, layer_acceptance = stratified_rejection_sampling(
        target_pdf, domains, proposal_funcs, n_samples=2000
    )
    stratified_time = time.time() - start_time
    
    print(f"分层拒绝采样 - 平均接受率: {np.mean(layer_acceptance):.4f}, 时间: {stratified_time:.4f}s")
    print(f"  各层接受率: {layer_acceptance}")
    
    # 方法4: 混合提议分布拒绝采样
    proposal_components = [
        {'pdf': lambda x: stats.norm.pdf(x, -3, 1), 'rv': lambda: np.random.normal(-3, 1), 'weight': 0.3},
        {'pdf': lambda x: stats.norm.pdf(x, 0, 1.5), 'rv': lambda: np.random.normal(0, 1.5), 'weight': 0.4},
        {'pdf': lambda x: stats.norm.pdf(x, 3, 1), 'rv': lambda: np.random.normal(3, 1), 'weight': 0.3},
    ]
    
    mixture_sampler = MixtureProposalSampler(target_pdf, proposal_components)
    
    start_time = time.time()
    mixture_samples, mixture_acceptance = mixture_sampler.sample(n_samples=2000)
    mixture_time = time.time() - start_time
    
    print(f"混合提议分布 - 接受率: {mixture_acceptance:.4f}, 时间: {mixture_time:.4f}s")
    
    # 可视化结果
    fig, axes = plt.subplots(2, 3, figsize=(15, 10))
    
    # 绘制目标分布
    x_vals = np.linspace(-10, 10, 1000)
    target_vals = target_pdf(x_vals)
    
    # 子图1: 基础拒绝采样
    axes[0, 0].hist(basic_samples, bins=50, density=True, alpha=0.6, color='blue', label='采样分布')
    axes[0, 0].plot(x_vals, target_vals, 'r-', linewidth=2, label='目标分布')
    axes[0, 0].set_title(f'基础拒绝采样\n接受率: {basic_acceptance:.4f}')
    axes[0, 0].legend()
    axes[0, 0].grid(True, alpha=0.3)
    
    # 子图2: 自适应拒绝采样
    axes[0, 1].hist(adaptive_samples, bins=50, density=True, alpha=0.6, color='green', label='采样分布')
    axes[0, 1].plot(x_vals, target_vals, 'r-', linewidth=2, label='目标分布')
    axes[0, 1].set_title(f'自适应拒绝采样\n接受率: {adaptive_acceptance:.4f}')
    axes[0, 1].legend()
    axes[0, 1].grid(True, alpha=0.3)
    
    # 子图3: 分层拒绝采样
    axes[0, 2].hist(stratified_samples, bins=50, density=True, alpha=0.6, color='orange', label='采样分布')
    axes[0, 2].plot(x_vals, target_vals, 'r-', linewidth=2, label='目标分布')
    axes[0, 2].set_title(f'分层拒绝采样\n平均接受率: {np.mean(layer_acceptance):.4f}')
    axes[0, 2].legend()
    axes[0, 2].grid(True, alpha=0.3)
    
    # 子图4: 混合提议分布
    axes[1, 0].hist(mixture_samples, bins=50, density=True, alpha=0.6, color='purple', label='采样分布')
    axes[1, 0].plot(x_vals, target_vals, 'r-', linewidth=2, label='目标分布')
    axes[1, 0].set_title(f'混合提议分布\n接受率: {mixture_acceptance:.4f}')
    axes[1, 0].legend()
    axes[1, 0].grid(True, alpha=0.3)
    
    # 子图5: 接受率比较
    methods = ['基础', '自适应', '分层', '混合']
    acceptances = [basic_acceptance, adaptive_acceptance, np.mean(layer_acceptance), mixture_acceptance]
    times = [basic_time, adaptive_time, stratified_time, mixture_time]
    
    x_pos = np.arange(len(methods))
    axes[1, 1].bar(x_pos, acceptances, color=['blue', 'green', 'orange', 'purple'])
    axes[1, 1].set_xticks(x_pos)
    axes[1, 1].set_xticklabels(methods)
    axes[1, 1].set_ylabel('接受率')
    axes[1, 1].set_title('各方法接受率比较')
    axes[1, 1].grid(True, alpha=0.3, axis='y')
    
    # 在柱状图上显示数值
    for i, v in enumerate(acceptances):
        axes[1, 1].text(i, v + 0.01, f'{v:.4f}', ha='center')
    
    # 子图6: 时间比较
    axes[1, 2].bar(x_pos, times, color=['blue', 'green', 'orange', 'purple'])
    axes[1, 2].set_xticks(x_pos)
    axes[1, 2].set_xticklabels(methods)
    axes[1, 2].set_ylabel('时间 (秒)')
    axes[1, 2].set_title('各方法时间消耗比较')
    axes[1, 2].grid(True, alpha=0.3, axis='y')
    
    # 在柱状图上显示数值
    for i, v in enumerate(times):
        axes[1, 2].text(i, v + 0.01, f'{v:.4f}', ha='center')
    
    plt.tight_layout()
    plt.show()
    
    # 返回结果供进一步分析
    results = {
        'basic': {'samples': basic_samples, 'acceptance': basic_acceptance, 'time': basic_time},
        'adaptive': {'samples': adaptive_samples, 'acceptance': adaptive_acceptance, 'time': adaptive_time},
        'stratified': {'samples': stratified_samples, 'acceptance': np.mean(layer_acceptance), 'time': stratified_time},
        'mixture': {'samples': mixture_samples, 'acceptance': mixture_acceptance, 'time': mixture_time}
    }
    
    return results

# ==================== 测试和演示 ====================
if __name__ == "__main__":
    print("拒绝采样算法优化与微调模拟")
    print("=" * 60)
    
    # 定义目标分布：混合高斯分布
    def target_pdf(x):
        # 两个高斯分布的混合
        return 0.7 * stats.norm.pdf(x, -2, 1) + 0.3 * stats.norm.pdf(x, 3, 1.5)
    
    # 比较不同采样方法
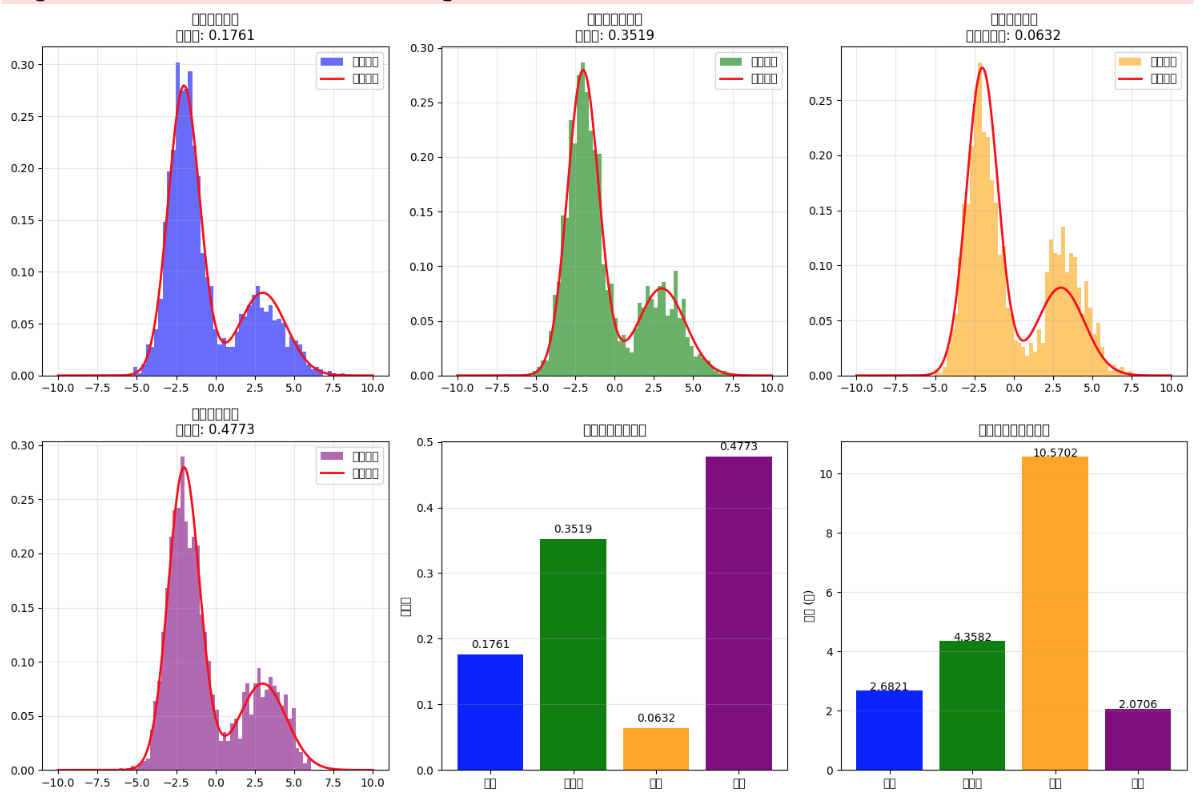
    results = compare_sampling_methods(target_pdf)

python模拟输出如下所示

虽然，由于中文字体原因，图例不是很清晰，但依然能看出代码较好的拟合了双峰高斯分布。

拒绝采样算法优化与微调模拟

============================================================

目标分布: 混合高斯分布

============================================================

基础拒绝采样 - 使用的M值: 5.7572

基础拒绝采样 - 接受率: 0.1761, 时间: 2.6821s

自适应拒绝采样 - 接受率: 0.3519, 时间: 4.3582s

分层拒绝采样 - 平均接受率: 0.0632, 时间: 10.5702s

各层接受率: [0.030725999631472267, 0.07261049423035053, 0.0863925282137761]

混合提议分布 - 接受率: 0.4773, 时间: 2.0706s

2.2 拒绝采样优化模拟总结

对于简单分布，基础拒绝采样通常足够；对于复杂多峰分布，自适应或分层方法更有效；混合提议分布可以更好地匹配目标分布的形状。

对于优化和模拟拒绝采样，需要注意以下几点：

• 选择合适的提议分布以匹配目标分布

• 找到尽可能小的M值以提高接受率

• 对于不同区域使用不同的提议分布（分层/混合）

reference

---