【图像处理基石】图像梯度：核心算法原理与经典应用场景全解析

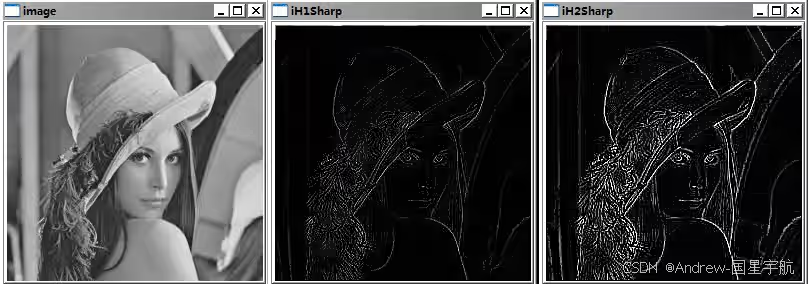
在图像处理与计算机视觉领域，图像梯度是描述图像像素值变化率的核心概念，它不仅揭示了图像中边缘、纹理等关键结构信息，更是众多高级视觉任务的基础。从基础的边缘检测到复杂的特征提取、图像分割，图像梯度都扮演着不可替代的角色。本文将从梯度的数学本质出发，深入解析经典的梯度计算算法，结合实际应用场景展开分析，并提供可直接运行的Python代码实现，帮助工程师快速掌握这一核心技术。

一、图像梯度的数学本质

在数学中，梯度是一个向量，用于描述多元函数在某一点的变化率最大的方向 和变化程度 。对于二维灰度图像而言，其像素值可视为二维函数 I ( x , y ) I(x,y) I(x,y)，其中 ( x , y ) (x,y) (x,y)为像素坐标， I I I为灰度值。

图像梯度的计算分为两个部分：

x方向梯度（ G x G_x Gx） ：描述像素值在水平方向的变化率，对应函数对 x x x的偏导数 ∂ I ∂ x \frac{\partial I}{\partial x} ∂x∂I
y方向梯度（ G y G_y Gy） ：描述像素值在垂直方向的变化率，对应函数对 y y y的偏导数 ∂ I ∂ y \frac{\partial I}{\partial y} ∂y∂I

梯度的幅值（Magnitude） 表示像素值的变化程度，计算公式为：
G = G x 2 + G y 2 G = \sqrt{G_x^2 + G_y^2} G=Gx2+Gy2

为了简化计算，工程中常使用绝对值近似：
G ≈ ∣ G x ∣ + ∣ G y ∣ G \approx |G_x| + |G_y| G≈∣Gx∣+∣Gy∣

梯度的方向（Direction） 表示像素值变化最大的方向，计算公式为：
θ = arctan ⁡ ( G y G x ) \theta = \arctan\left(\frac{G_y}{G_x}\right) θ=arctan(GxGy)

需要注意的是，数字图像是离散的像素矩阵，无法直接计算连续函数的偏导数，因此实际应用中通常采用差分运算来近似梯度，这也是所有梯度计算算法的核心思想。

二、经典梯度计算算法原理与对比

基于差分思想，研究者提出了多种梯度计算算法，不同算法在卷积核设计、噪声鲁棒性、计算精度等方面各有优劣。以下是工程中最常用的5种经典算法：

1. Roberts算子：一阶交叉差分算子

原理：Roberts算子是最简单的梯度算子，采用2×2卷积核进行交叉差分，分别计算对角线方向的差分来近似 G x G_x Gx和 G y G_y Gy。

卷积核形式：
G x = [ 1 0 0 − 1 ] , G y = [ 0 1 − 1 0 ] G_x = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}, \quad G_y = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} Gx=[100−1],Gy=[0−110]

优缺点：

优点：计算简单、速度快，对陡峭边缘的检测效果好
缺点：对噪声非常敏感，无法抑制噪声；仅考虑2×2邻域，精度较低

适用场景：无噪声或低噪声的简单图像边缘检测

2. Prewitt算子：邻域平均差分算子

原理：Prewitt算子采用3×3卷积核，通过对邻域像素进行平均后再差分，从而提高对噪声的抑制能力。

卷积核形式：
G x = [ − 1 0 1 − 1 0 1 − 1 0 1 ] , G y = [ − 1 − 1 − 1 0 0 0 1 1 1 ] G_x = \begin{bmatrix} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \end{bmatrix}, \quad G_y = \begin{bmatrix} -1 & -1 & -1 \\ 0 & 0 & 0 \\ 1 & 1 & 1 \end{bmatrix} Gx= −1−1−1000111 ,Gy= −101−101−101

优缺点：

优点：通过邻域平均抑制噪声，对边缘的检测效果比Roberts更稳定
缺点：对边缘的定位精度一般，未考虑像素间的距离权重

适用场景：中等噪声场景下的边缘检测

3. Sobel算子：加权邻域差分算子

原理：Sobel算子是工程中最常用的梯度算子，在Prewitt算子的基础上，对邻域像素进行加权平均 （距离中心像素越近，权重越大），进一步提高噪声鲁棒性和梯度计算精度。

卷积核形式：
G x = [ − 1 0 1 − 2 0 2 − 1 0 1 ] , G y = [ − 1 − 2 − 1 0 0 0 1 2 1 ] G_x = \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix}, \quad G_y = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix} Gx= −1−2−1000121 ,Gy= −101−202−101

优缺点：

优点：噪声鲁棒性好，梯度计算精度高，计算速度快
缺点：对边缘的定位精度仍有提升空间，在小卷积核下对斜向边缘的检测效果一般

适用场景：大多数通用场景的边缘检测、特征提取，是OpenCV等库的默认梯度算子

4. Scharr算子：Sobel的高精度改进版

原理：Scharr算子是对Sobel算子的改进，通过优化卷积核的权重系数，在保持3×3小卷积核的前提下，进一步提高梯度计算的精度，尤其是对斜向边缘的检测精度。

卷积核形式：
G x = [ − 3 0 3 − 10 0 10 − 3 0 3 ] , G y = [ − 3 − 10 − 3 0 0 0 3 10 3 ] G_x = \begin{bmatrix} -3 & 0 & 3 \\ -10 & 0 & 10 \\ -3 & 0 & 3 \end{bmatrix}, \quad G_y = \begin{bmatrix} -3 & -10 & -3 \\ 0 & 0 & 0 \\ 3 & 10 & 3 \end{bmatrix} Gx= −3−10−30003103 ,Gy= −303−10010−303

优缺点：

优点：比Sobel算子的精度更高，对斜向边缘的检测效果更好，同样具有噪声鲁棒性
缺点：计算量略大于Sobel算子

适用场景：对边缘定位精度要求较高的场景，如精密零件检测、医学图像分析

5. Laplacian算子：二阶差分算子

原理：Laplacian算子是二阶差分算子，描述的是梯度的变化率，而非梯度本身。它通过计算二阶偏导数的和来检测图像中的零交叉点 （边缘处的梯度变化率最大，对应Laplacian的零交叉点）。

卷积核形式（4邻域）：
∇ 2 I = [ 0 1 0 1 − 4 1 0 1 0 ] \nabla^2 I = \begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{bmatrix} ∇2I= 0101−41010

优缺点：

优点：对边缘的定位精度高，能检测到所有方向的边缘
缺点：对噪声非常敏感，会放大噪声；无法区分边缘的方向

适用场景：边缘定位、图像锐化（如Unsharp Mask算法）

经典梯度算法对比表

算法	卷积核大小	噪声鲁棒性	边缘定位精度	计算速度	适用场景
Roberts	2×2	差	一般	最快	低噪声简单图像边缘检测
Prewitt	3×3	中	一般	快	中等噪声边缘检测
Sobel	3×3	好	较好	较快	通用场景边缘检测、特征提取
Scharr	3×3	好	好	较快	高精度边缘检测
Laplacian	3×3	差	好	快	边缘定位、图像锐化

三、图像梯度的经典应用场景

图像梯度的应用贯穿于图像处理的各个环节，从基础的边缘检测到复杂的目标识别，都离不开梯度信息的支持。以下是5个最经典的应用场景：

1. 边缘检测：最基础的应用

边缘是图像中最基本的特征，指的是像素值发生剧烈变化的区域，对应梯度幅值较大的区域。边缘检测是目标识别、图像分割等高级任务的预处理步骤。

实现思路：

对图像进行灰度化和去噪（如高斯滤波）
采用梯度算法计算梯度幅值
通过阈值分割提取边缘（如非极大值抑制、双阈值检测）

经典算法：Canny边缘检测算法（融合了高斯滤波、Sobel梯度计算、非极大值抑制、双阈值检测，是目前最优秀的边缘检测算法）

2. 图像分割：基于梯度的区域划分

图像分割的目标是将图像划分为不同的区域，梯度信息可以帮助区分不同区域的边界。

典型应用：

阈值分割：通过梯度幅值的阈值将图像分为边缘和非边缘区域
分水岭算法：将梯度幅值图像作为输入，梯度大的区域作为分水岭，避免过度分割
边缘检测分割：通过检测边缘并连接成闭合区域，实现区域划分

3. 特征提取：梯度方向直方图（HOG）

在目标检测中，梯度方向直方图（Histogram of Oriented Gradients，HOG）是一种经典的特征描述子，广泛应用于行人检测、车辆检测等场景。

原理：

将图像划分为单元格（cell）和块（block）
计算每个单元格内的梯度方向和幅值
统计每个单元格的梯度方向直方图（以幅值为权重）
对块内的直方图进行归一化，得到HOG特征

优势：HOG特征能有效描述目标的形状和纹理信息，对光照变化和小幅度形变具有鲁棒性。

4. 图像增强：基于梯度的锐化

图像锐化的目标是增强图像的边缘和纹理细节，使图像更加清晰。基于梯度的锐化算法通过增强梯度幅值来实现锐化效果。

经典算法 ：Unsharp Mask算法
原理：

对原图像进行高斯滤波，得到模糊图像
计算原图像与模糊图像的差值（残差图像，对应梯度信息）
将残差图像加权后叠加到原图像上，实现锐化

5. 运动检测：光流法中的梯度应用

光流法是用于检测图像中像素运动的算法，其核心方程（光流约束方程）基于梯度信息推导：
I x u + I y v + I t = 0 I_x u + I_y v + I_t = 0 Ixu+Iyv+It=0

其中， I x I_x Ix和 I y I_y Iy是空间梯度， I t I_t It是时间梯度， u u u和 v v v是像素在x和y方向的运动速度。

原理：通过计算空间梯度和时间梯度，求解光流约束方程，得到像素的运动速度，从而实现运动检测。

四、Python代码实现：经典梯度算法与边缘检测

以下是基于Python+OpenCV的经典梯度算法实现代码，包括Sobel、Scharr、Laplacian算子的梯度计算和边缘检测，以及梯度幅值和方向的计算。

1. 环境准备

确保安装了以下库：

bash 复制代码

pip install opencv-python numpy matplotlib

2. 代码实现

python 复制代码

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像并转换为灰度图
img = cv2.imread("test.jpg")
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 1. 高斯滤波去噪（可选，用于提高噪声鲁棒性）
blur = cv2.GaussianBlur(gray, (3, 3), 0)

# 2. 计算经典梯度算子的边缘检测结果
# Sobel算子
sobel_x = cv2.Sobel(blur, cv2.CV_64F, 1, 0, ksize=3)  # x方向梯度
sobel_y = cv2.Sobel(blur, cv2.CV_64F, 0, 1, ksize=3)  # y方向梯度
sobel_abs_x = cv2.convertScaleAbs(sobel_x)  # 转换为绝对值
sobel_abs_y = cv2.convertScaleAbs(sobel_y)
sobel_edge = cv2.addWeighted(sobel_abs_x, 0.5, sobel_abs_y, 0.5, 0)  # 合并x和y方向边缘

# Scharr算子
scharr_x = cv2.Scharr(blur, cv2.CV_64F, 1, 0)
scharr_y = cv2.Scharr(blur, cv2.CV_64F, 0, 1)
scharr_abs_x = cv2.convertScaleAbs(scharr_x)
scharr_abs_y = cv2.convertScaleAbs(scharr_y)
scharr_edge = cv2.addWeighted(scharr_abs_x, 0.5, scharr_abs_y, 0.5, 0)

# Laplacian算子
laplacian = cv2.Laplacian(blur, cv2.CV_64F, ksize=3)
laplacian_edge = cv2.convertScaleAbs(laplacian)

# 3. 计算梯度幅值和方向
# 方法1：精确计算（sqrt(Gx^2 + Gy^2)）
gradient_magnitude = np.sqrt(sobel_x ** 2 + sobel_y ** 2)
gradient_magnitude = cv2.convertScaleAbs(gradient_magnitude)  # 转换为8位图像

# 方法2：近似计算（|Gx| + |Gy|）
gradient_magnitude_approx = cv2.addWeighted(sobel_abs_x, 1, sobel_abs_y, 1, 0)

# 计算梯度方向（弧度制）
gradient_direction = np.arctan2(sobel_y, sobel_x)

# 4. 显示结果
plt.figure(figsize=(12, 8))
plt.subplot(2, 3, 1), plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB)), plt.title("Original Image"), plt.axis("off")
plt.subplot(2, 3, 2), plt.imshow(sobel_edge, cmap="gray"), plt.title("Sobel Edge"), plt.axis("off")
plt.subplot(2, 3, 3), plt.imshow(scharr_edge, cmap="gray"), plt.title("Scharr Edge"), plt.axis("off")
plt.subplot(2, 3, 4), plt.imshow(laplacian_edge, cmap="gray"), plt.title("Laplacian Edge"), plt.axis("off")
plt.subplot(2, 3, 5), plt.imshow(gradient_magnitude, cmap="gray"), plt.title("Gradient Magnitude"), plt.axis("off")
plt.subplot(2, 3, 6), plt.imshow(gradient_magnitude_approx, cmap="gray"), plt.title("Gradient Magnitude (Approx)"), plt.axis("off")
plt.tight_layout()
plt.show()

3. 代码说明

代码中首先对图像进行高斯滤波去噪，这是提高梯度算法噪声鲁棒性的重要步骤
采用cv2.Sobel、cv2.Scharr、cv2.Laplacian函数分别实现经典梯度算法
计算了梯度幅值的精确值和近似值，近似值在工程中更常用（计算速度快）
通过Matplotlib显示了原始图像、不同算法的边缘检测结果和梯度幅值图像

五、总结与工程实践建议

图像梯度是图像处理的核心概念，其应用贯穿于从基础到高级的各个视觉任务。本文从数学本质出发，解析了5种经典梯度计算算法的原理与对比，结合5个经典应用场景展开分析，并提供了可直接运行的Python代码实现。

工程实践建议

算法选择 ：
- 通用场景优先选择Sobel算子（平衡了精度、速度和噪声鲁棒性）
- 高精度场景选择Scharr算子（如精密检测、医学图像）
- 简单场景选择Prewitt算子（计算速度快）
- 边缘定位场景选择Laplacian算子（需配合去噪）
预处理步骤 ：
- 梯度算法对噪声敏感，建议在计算梯度前进行高斯滤波去噪
- 对彩色图像，需先转换为灰度图再计算梯度
后处理步骤 ：
- 边缘检测后可采用非极大值抑制、双阈值检测等方法优化边缘结果
- 梯度幅值图像可通过阈值分割提取关键边缘

六、拓展思考

图像梯度的应用远不止本文提到的场景，随着深度学习的发展，梯度信息也被融入到卷积神经网络中（如卷积层的梯度计算、边缘检测网络如HED）。未来，结合传统梯度算法和深度学习的优势，将成为图像处理领域的重要研究方向。